B样条快速求值改进CST参数化方法*

闫博文 黄 俊 刘志勤 王耀彬

西南科技大学计算机科学与技术学院，四川绵阳 621000

随着航空航天技术的发展和国防科技的需求，飞行器的外形设计越来越受关注，飞行器设计的第一步便是外形参数化，它的优劣程度对于飞机设计的成功与否有着至关重要的影响，直接影响着总体项目的进度。一个好的参数化方法应该具备以下特性：1)较大的寻优空间；2)良好的局部控制能力，以及较少的设计变量；3)保证在优化过程中飞机的几何外形是光滑的[1-2]。

Kulfan和Bussoletti提出了一种比较优秀的参数化方法：CST技术。CST技术同时使用类别函数与形状函数来对外形进行控制，类别函数(Class Function)生成几何图形的基本外形，再通过形状函数(Shape Function)对这个基本的几何图形进行修正，从而得到所需要的几何外形。因该技术具有设计变量少，可调节，设计空间广，可产生光滑的几何外形，以及较好的鲁棒性等优点而被广泛应用在飞行器外形参数化的设计中[3-5]。由于Bezier多项式对局部几何特性描述能力不足，王迅等人提出了使用B样条函数替代Bezier多项式构造形函数的改进方法，以提高对外形的局部描述能力[6]，因为B样条方法在数据的拟合、平滑和插值等方面有良好的效果，所以在阶数较小的情况下，该方法确实起到了优化作用。但B样条基函数为分段函数，无法使用统一的解析式表达，大多使用迭代方法求值，会出现多次重复计算，随着阶数的增加，计算量也急剧增加，文献[6]也只采用了3阶来进行证明。因此，只有解决B样条在高阶数计算量大的问题，找出一种快速求解的算法，提高运算效率，才能让B样条改进CST方法发挥出更大的价值。因此，本文主要研究B样条基函数快速求值改进CST算法。

1 B样条替代Bezier多项式建模

1.1 B样条基函数定义

B样条的基函数有许多定义方法，它们中最被大家广泛认可的是de Boor-Cox递推定义法，因为de Boor-Cox递推定义充分展示了B样条基函数的性质，并给出了明确的B样条基函数递推求解算法，故本文将其作为B样条基函数的标准定义[7]。

基函数定义：

(1)

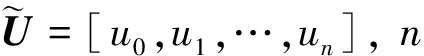
1.2 替代Bezier多项式的CST方法建模

一般机翼的CST方法数学表达式：

(2)

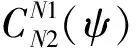
(3)

修改后的B样条基函数CST公式对求解时出现的病态现象有很大的缓解，求解更加稳定，具有很好的局部描写能力。

2 B样条基函数快速求值算法

2.1 de Boor-Cox算法弊端

在实际计算B样条时,往往不需要将整个B样条数值全部计算出来，有时只需要计算某一参数值处的B样条基函数。由B样条局部支撑性质，可知当参数u∈[ui,ui+1),只需计算出Nm,k(u),m=i-k,i-k+1,…,i；而其他k次B样条在该处均为0。

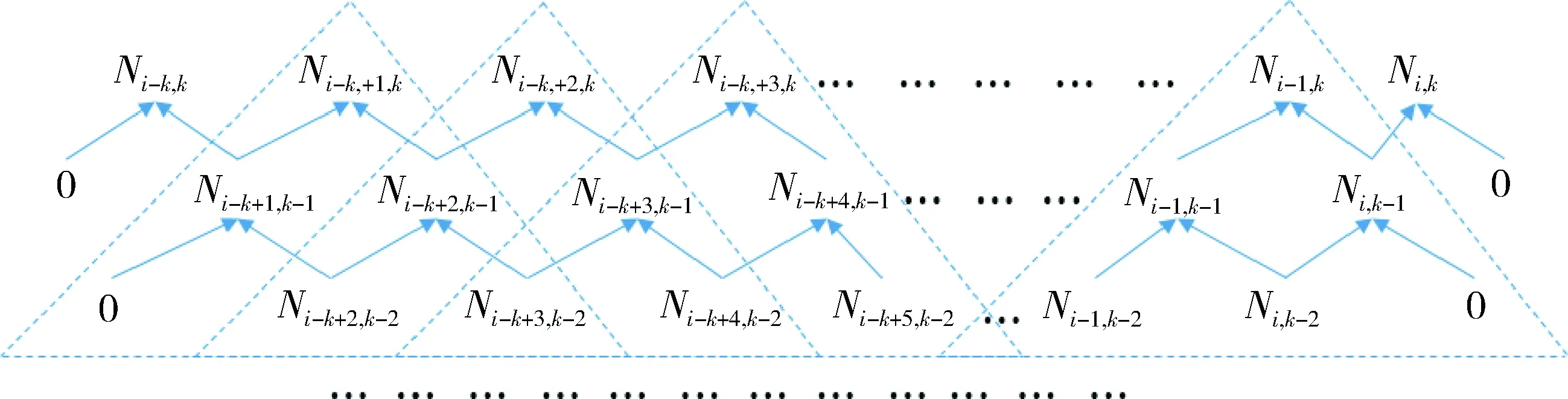
图1 B样条基函数运算路径

图1中，B样条基函数计算过程已用虚线三角形标出，可以直观的看到，每一个基函数不仅依赖于它下一层相邻的2个基函数，而且还影响它上一层相邻的2个基函数。显然，式(1)的计算方法并不能充分利用这种网格结构，存在大量的重复计算，例如2个虚线三角形重叠的部分就是重复计算的部分，故而要加快B样条基函数求解效率就要从这里着手。

2.2 准备工作

为后续阐述B样条基函数快速求值首先定义一种向量扩展算法。

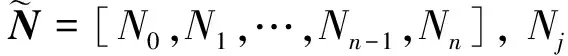
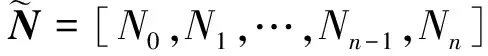
Zj=Nj+Qj-1-Qj

(4)

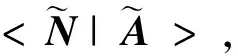
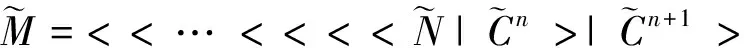
这种递推式的运算有利于使用计算机运算，称定义3给出的运算为向量递推扩展运算。

2.3 快速求解算法证明[8]

首先，对将要使用的符号进行说明：

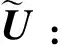
Nj,m(u):表示m次B样条第j个样条基函数，其中，m=0,1,2,…,k；j=1,2,3；

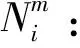
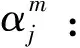
(5)

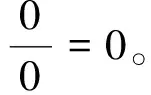
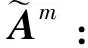
证明B样条基函数快速求值前，还需证明引理1。

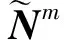
根据定义2的向量扩展运算法，则有：

(6)

其中：0≤j≤m，规定向量下标溢出时对应元素置0。

(7)

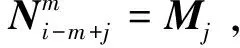
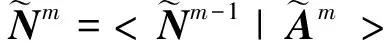
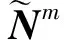
再由定义(1)可知：

定理1提供了实现B样条基函数求值的向量递推扩展方法。其计算路径如图2。由图2可知，B样条基函数向量扩展快速求值方法正是一种网状计算结构，它是以1维的单位向量{[1]}为主向量，通过递推扩展，实现了同次数B样条基函数值的同步计算(图2中虚线方框部分)。向量递推扩展方法避免了重复计算，提高了计算效率，这由图2算法计算路径没有重叠部分可以充分说明。综上所述，B样条的向量扩展求值算法在计算路径上比式(1)的de Boor-Cox算法效率更高。

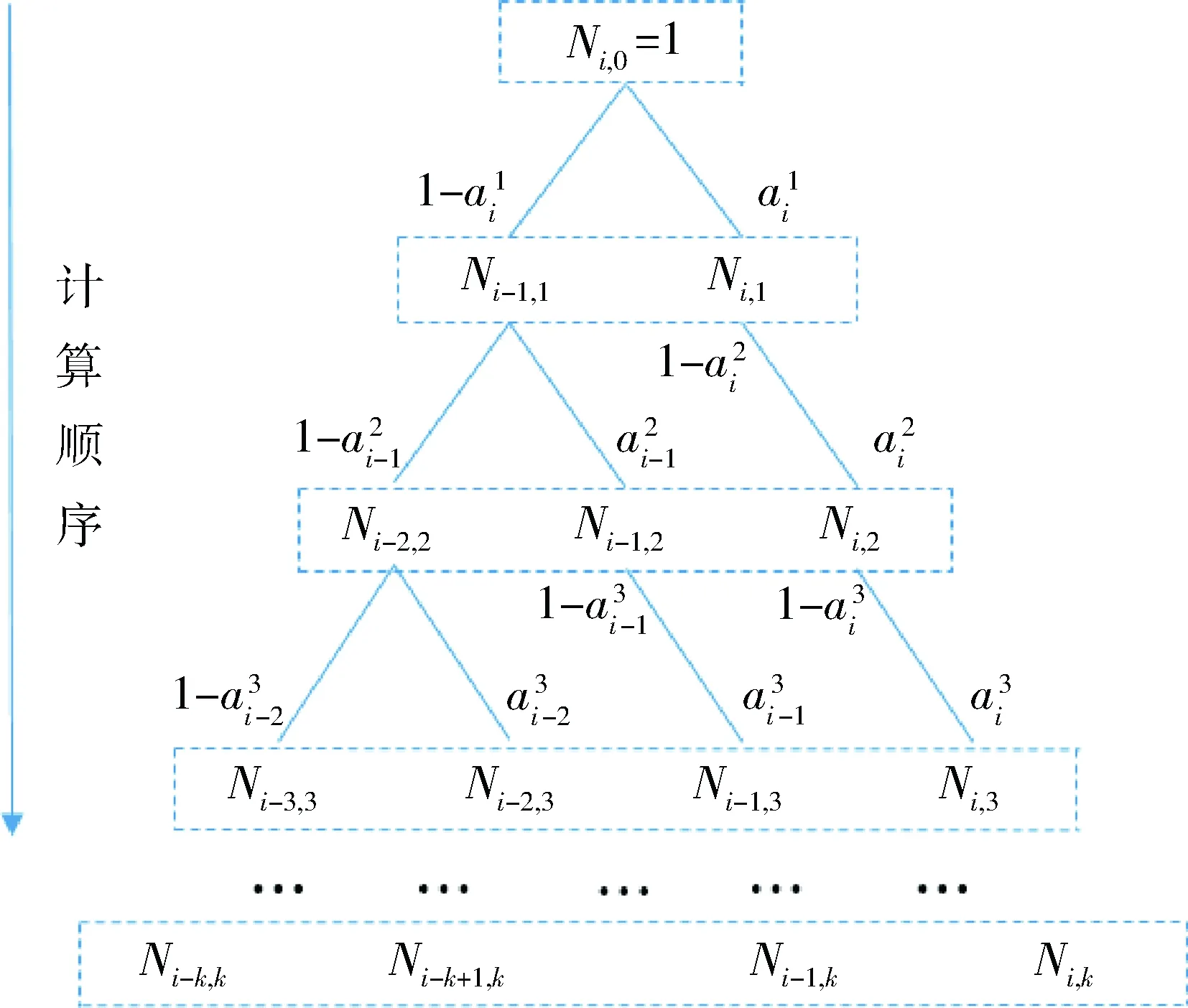
图2 B样条向量扩展法基函数运算路径

2.4 算法效率

同de Boor-Cox递推定义法相比，式(4)的B样条基函数向量扩展求值算法效率更高，计算k次B样条基函数非零值，统计对比式(1)与式(4)的运算次数，可得：使用向量同步递推运算获得k+1个非零基函数值的计算效率是使用de Boor-Cox递推方法的2k+1倍。

表1 k次B样条的(k+1)个非零基函数运算量对比

3 应用展示

3.1 B样条快速求值CST二维建模

图3为使用B样条快速求值CST方法生成的二维图形。

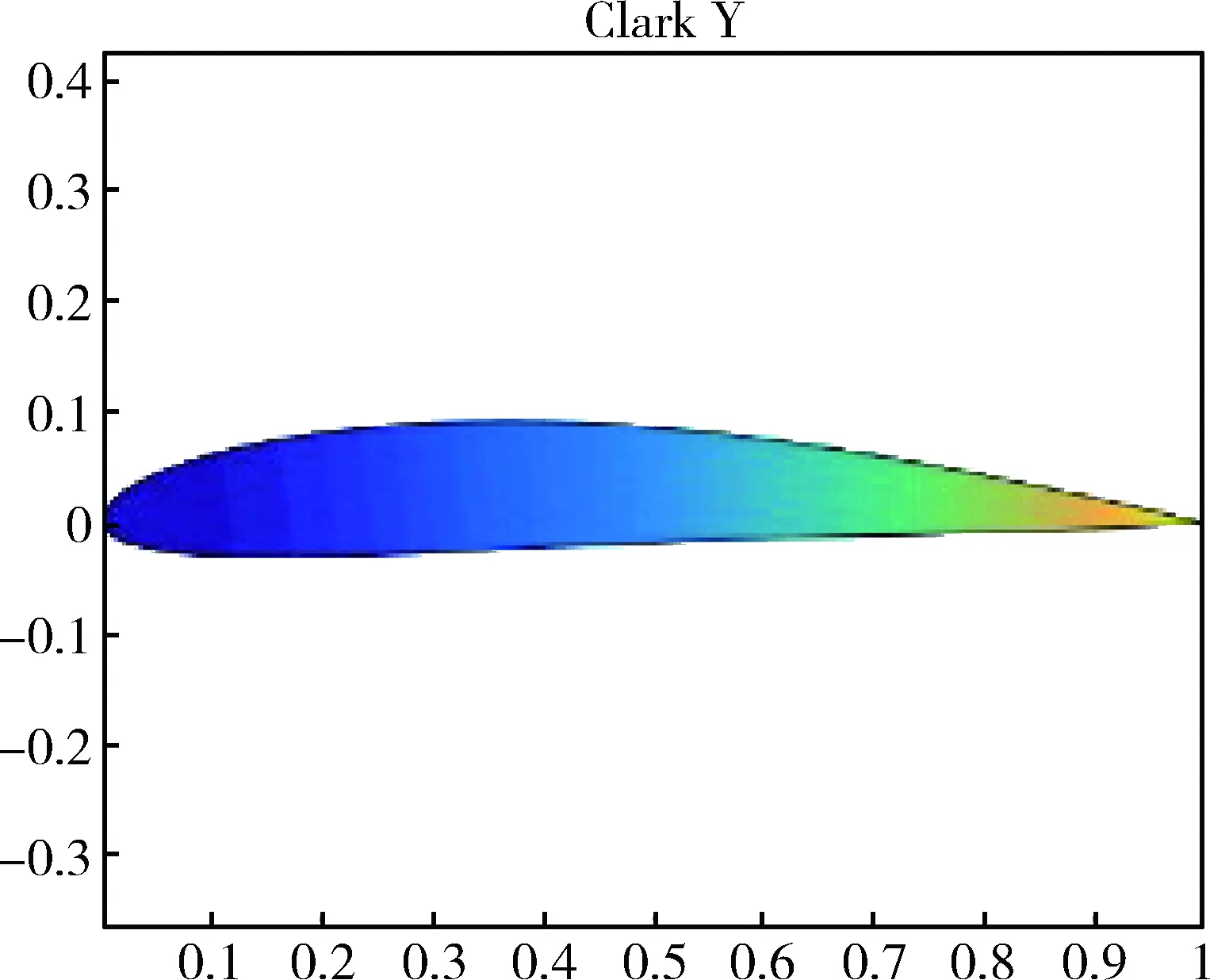
图3 B样条向量扩展法模拟Clark-Y机翼

3.2 B样条快速求值CST三维建模

3.2.1 局部控制展示

图4中，(a)图展示使用B样条快速求值方法控制横截面从圆形渐变到正方形，(b)图展示截面函数指数NC随着长度的增加而进行变化，若将该立体图形的总长度视为100%，在总长度的0%～20%区间内，立体图形的横截面是标准圆形，NC=0.5；在总长度的95%～100%区间内，立体图形的横截面是标准的正方形，NC=0.005，在总长度的20%～95%区间内，函数指数随长度的增加而减小。

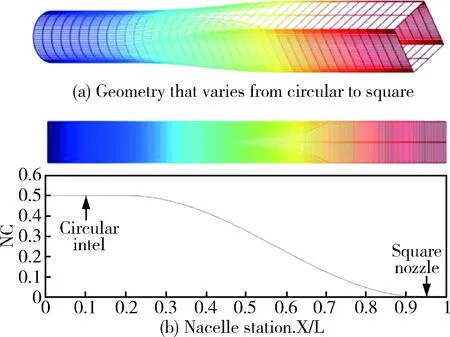
图4 B样条快速求值局部控制展示

3.2.2 B样条快速求值CST方法三维机翼

三维机翼其实本质上可以看成是二维机翼的扩展，扩展时需要注意控制外形的变化。

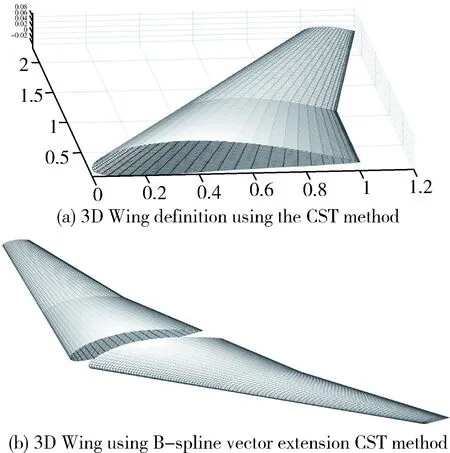
图5 CST算法三维机翼展示

4 结论

通过B样条改进CST参数化方法，提高了CST算法的局部控制能力，同时使用向量扩展方法实现B样条快速求值，提高了B样条CST算法的计算效率，增大了设计空间，提高了可控性，为提高后续翼型气动优化的精度，最终得到良好的气动外形奠定了基础。

[1] Isakova N P, Kraiko A A, P’Yankov K S. Direct Method for the Design of Optimal Three-dimensional Aerodynamic Shapes[J]. Computational Mathematics & Mathematical Physics, 2012, 52(11):1520-1525.

[2] 廖炎平, 刘莉, 龙腾. 几种翼型参数化方法研究[J]. 弹箭与制导学报, 2011, 31(3):160-164.(Liao Yanping, Liu Li, Long Teng. The Research on Some Param-eterized Methods for Airfoil[J]. Journal of Projectiles Rockets Missiles & Guidance, 2011, 31(3):160-164.)

[3] Kulfan B. A Universal Parametric Geometry Representa-tion Method - "CST"[C]. AIAA--2007-0062, Jan 2007

[4] Kulfan, B. M, Bussoletti, J. E., Fundamental Parametric Geometry Representations for Aircraft Component Shapes[C]. AIAA-2006-6948, 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference: The Modeling and Simulation Frontier for Multidisciplinary Design Optimization, 6 - 8 September, 2006

[5] Ciampa P D, Zill T, Nagel B. CST Parametrization for Unconventional Aircraft Design Optimization[C].Congress of the International Council of the Aerospace Sciences. DLR, 2010.

[6] 王迅, 蔡晋生, 屈崑,等. 基于改进CST参数化方法和转捩模型的翼型优化设计[J]. 航空学报, 2015, 36(2):449-461.(Wang Xun，Cai Jinsheng，Qu K，et al. Airfoil Optimization Based on Improved CST Parametric Method and Transition Model[J]. Acta Aeronautica et Astronautica Sinica，2015,36(2)：449-461.)

[7] Piegl L, Tiller W. The NURBS, Book[M]. Springer Ber-lin Heidelberg, 1997.

[8] 孙海洋, 范大鹏. B样条快速求值算法及其在数控插补中的应用[J]. 计算机工程与应用, 2007, 43(34):81-84.(Sun Haiyang, Fan Dapeng.Fast Algorithm to Compute B-spline Functions and Its Application in CNC Interpolation[J]. Computer Engineering and Applications,2007,43(34)：81-84.)