基于极点对称模态分解和概率神经网络的轴承故障诊断

张淑清 徐剑涛 姜安琦 李军锋 宿新爽 姜万录

1.燕山大学电气工程学院，秦皇岛，0660042.中南大学信息工程学院，长沙，4100063.燕山大学机械工程学院，秦皇岛，066004

基于极点对称模态分解和概率神经网络的轴承故障诊断

张淑清1徐剑涛1姜安琦2李军锋1宿新爽1姜万录3

1.燕山大学电气工程学院，秦皇岛，0660042.中南大学信息工程学院，长沙，4100063.燕山大学机械工程学院，秦皇岛，066004

针对复杂非线性的滚动轴承系统，提出了极点对称模态分解(ESMD)和概率神经网络(PNN)相结合的滚动轴承故障诊断方法。ESMD将固有模态函数的定义进行扩充，采用内部极点对称直接插值的方法替代外部包络线插值，引入最优的自适应全局曲线(AGM)的概念优化分解的趋势线，并由此确定最佳的模态分解次数。PNN是一种基于核函数逼近的神经网络分类器，将指数函数引入神经网络用来替代S型激活函数并进行重新构造，突出体现了梯度最速下降法的概念，减少实际和预测的输出函数之间的误差。通过对经验模态分解(EMD)、屏蔽经验模态分解(MEMD)和ESMD方法进行信号仿真分解对比，以及采用ESMD和PNN对故障数据进行处理，结果表明，该方法能够更加有效地对故障信号进行识别。

滚动轴承；极点对称模态分解；概率神经网络；故障诊断

0 引言

滚动轴承是旋转机械的重要组成部分，其振动信号是各种噪声和轴承的振动信号的叠加，具有非线性和非平稳性特征。处理方法包括傅里叶变换、小波变换以及自适应信号处理方法经验模态分解(empirical mode decomposition,EMD)等[1-3]。傅里叶变换和小波变换等时频信号分析方法都是由线性叠加原理发展而来的，对振动信号的非线性非平稳信号不适用[4]。EMD将采集的滚动轴承的振动信号进行包络分解，获得包含各个主分量的固有模态函数，从而体现出振动信号的特征分量信号[5]。然而其在信号分解过程中出现的模态混叠以及不能自适应地解决欠包络和过包络问题，限制了EMD处理信号的能力[6]。自适应信号处理方法屏蔽经验模态分解(masking empirical mode decomposition,MEMD) 使EMD法的混叠问题得到有效的解决[7]。然而，由于MEMD在处理信号的过程中添加了掩蔽信号，并且掩蔽信号的选择和处理具有不确定性，在信号的处理过程中不能完全综合所添加的信号，造成了其性能缺陷。

文献[8]研究极点对称模态分解算法，借鉴经验模态分解，采用内部极点对称直接插值的方法替代外部包络线插值，引入最优的自适应全局曲线(adaptive global mean,AGM)的概念来优化分解的趋势线，并由此确定最佳模态分解次数，取得了较好效果。

概率神经网络(probabilistic neural network,PNN)与BP(back propagation)神经网络相比具有一个相对较快的训练过程，这是因为预先设定的代表训练集的规模保证了最大化和训练样本可以随时添加或删除而无需广泛地再训[8]。

概率神经网络是一种基于核函数逼近的神经网络分类器，将指数函数引入神经网络用来替代S型激活函数并进行重新构造，突出体现了梯度最速下降法的概念，减小实际和预测的输出函数之间的误差。PNN在处理传统意义上复杂的、非线性的和不精确的问题时具有独特的优势。本文采用PNN神经网络故障数据进行处理，更加有效地对故障信号进行识别。

1 信号的ESMD分解

1.1 经验模态分解

经验模态分解的原理可以简单表述为

(1)

其中，R为残余量；cj为信号经过EMD分解所产生的固有模态函数(intrinsic mode function，IMF)[8],n为信号经EMD分解所产生的IMF的个数，j表示第j个IMF分量。

1.2 极点对称模态分解

经验模态分解中，所分解出的IMF分量不是完全正交的，如果信号中的极点分布不均匀或者极点数过于少，EMD分解就不能进行并且会出现模态混叠现象。极点对称模态分解的方法根据信号的特点，引入最优自适应全局曲线概念优化分解的趋势线，并由此确定最佳模态分解次数[9-11]。

ESMD重新定义了IMF:①局部的极大值点和极小值点是不同的，相邻且相等的极值点作为一个极值点加入到信号分解中，极大值必须是正数，极小值必须是负数；②广义上，IMF分量应该几乎是包络对称或者极点对称的。

ESMD并不将信号分解到最后剩余最多的一个极值点，相反，它允许残留成分包含一定数量的极值点。这一过程的优势一方面在于分解的残余分量可以反映整体数据的变化趋势，可以理解为一种最优的自适应全局曲线(adaptive global mean,AGM)；另一方面在于可以优化最小二乘法意义上的AGM曲线来确定最优的筛选次数。它提供了一个很好的自适应方法的数据拟合，优于一般的最小二乘法。

不同于EMD中构建两个不同的外部包络线，ESMD采用多次对极值点连线的重点进行内部曲线插值。根据以往实验，一般在数据处理中，两次内部曲线插值即可达到标准[9-11]。数据处理过程中，筛选次数的确定参考均值曲线的原理，采用最佳筛选次数的分解条件。

1.3 极点模态分解算法实现过程

(1) 用Ei(i=1,2,…，n)分别将信号X所有的极大值点和极小值点进行标记。

(2)用线段相互连接所有的极值点，并标记这些线段的中点为Fi(i=1,2,…，n-1)。

(3)通过一定的方法分别在左右两个边界添加F0和Fn。

(4)根据上述1+n个点构造p个内插值曲线L1,L2，…,Lp(p=1，2，…)，并且计算它们的均值：

L*=(L1+L2+…+Lp)/p

(2)

(5)令X-L*，并重复上述4个步骤，直到

|L*|≤ε

(3)

式中，ε为允许的误差。

或者筛选次数达到最大值K。此时，得到第一个模态函数M1。

(6)对于剩余部分X-M1重复上述5个步骤，可以依次得到M2,M3,…，直到最后的剩余分量R含有不超过约定的极点个数。

(7)在有限整数区间[Kmin,Kmax]改变最大筛选次数K的取值，重复上述6个步骤。然后计算X-R的方差σ2并作关于σ/σ0和K的曲线图，其中σ0为信号X的标准差。

(8)找到区间[Kmin,Kmax]中对应于σ/σ0最小值时K的最小值K0，用K0重复前6个步骤，得到最佳的ESMD分解出的各IMF分量。与此同时，得到的R即为最优的AGM曲线。

通常选择ε=0.001σ0，并且选择比率υ=σ/σ0去反映AGM曲线的最优程度。

此时原始数据和AGM曲线可分别用X={xi}和R={ri}表示，i=1,2,…,n。

定义数据的总体均值为

(4)

数据的方差为

(5)

AGM曲线的方差为

(6)

经过分解， 原始的时间序列X可表示为

(7)

利用ESMD将时间序列X分解成一系列IMF和一个趋势项。

1.4 ESMD与EMD、MEMD的对比

EMD将信号分解成包含不同主频分量的IMF分量，然而，当信号存在异常干扰或信号发生间断跳跃时，这些突变信号的频率往往要高于原信号的频率，出现模态混叠，无法将不同的主频分量有效地分离到不同的IMF分量中，使得一个固有模态函数分量中出现多个相近的主频分量，所以信号内部的特征无法真正通过EMD分解出的IMF分量表现出来[12]。模态混叠的出现导致EMD对信号的分解不能进行有效分析。屏蔽经验模态分解(MEMD)法由于掩蔽信号的不确定性造成其对信号的分解也会出现不确定性。

取两个等幅值的单频信号的叠加形式如下：

x1(t)=sin2πt+sin1.2πt

(8)

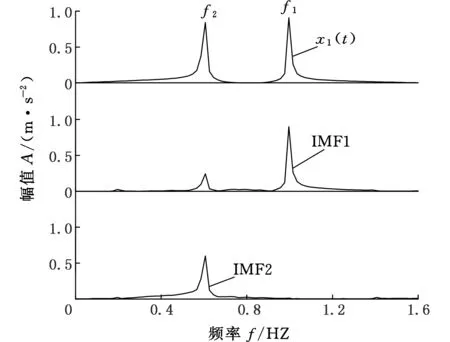
图1 x1(t)的EMD分解Fig.1 EMD of x1(t)

对该信号x1(t)进行EMD分解，如图1所示，信号x1(t)的频谱如图1a所示，f1=1 Hz,f2=0.6 Hz；图1b是EMD分解后的IMF1的频谱图。从图1b中可以看出，IMF1分量并不只包含一个主频率分量，它不仅包含主要的1 Hz高频成分而且含有部分0.6 Hz的低频成分，充分体现了经验模态分解过程中出现的模态混叠问题。在实际应用中，信号形式十分复杂，相邻的频率成分大小比较接近，难以区分，这就使得EMD分解不可避免地存在模态混叠问题。

采用ESMD对信号x1(t)进行处理后的频谱图见图2。通过对比图2和图1，可以看出ESMD分解后的IMF1分量中只包含单一的主频分量，不存在ESMD分解所存在的模态混叠问题。

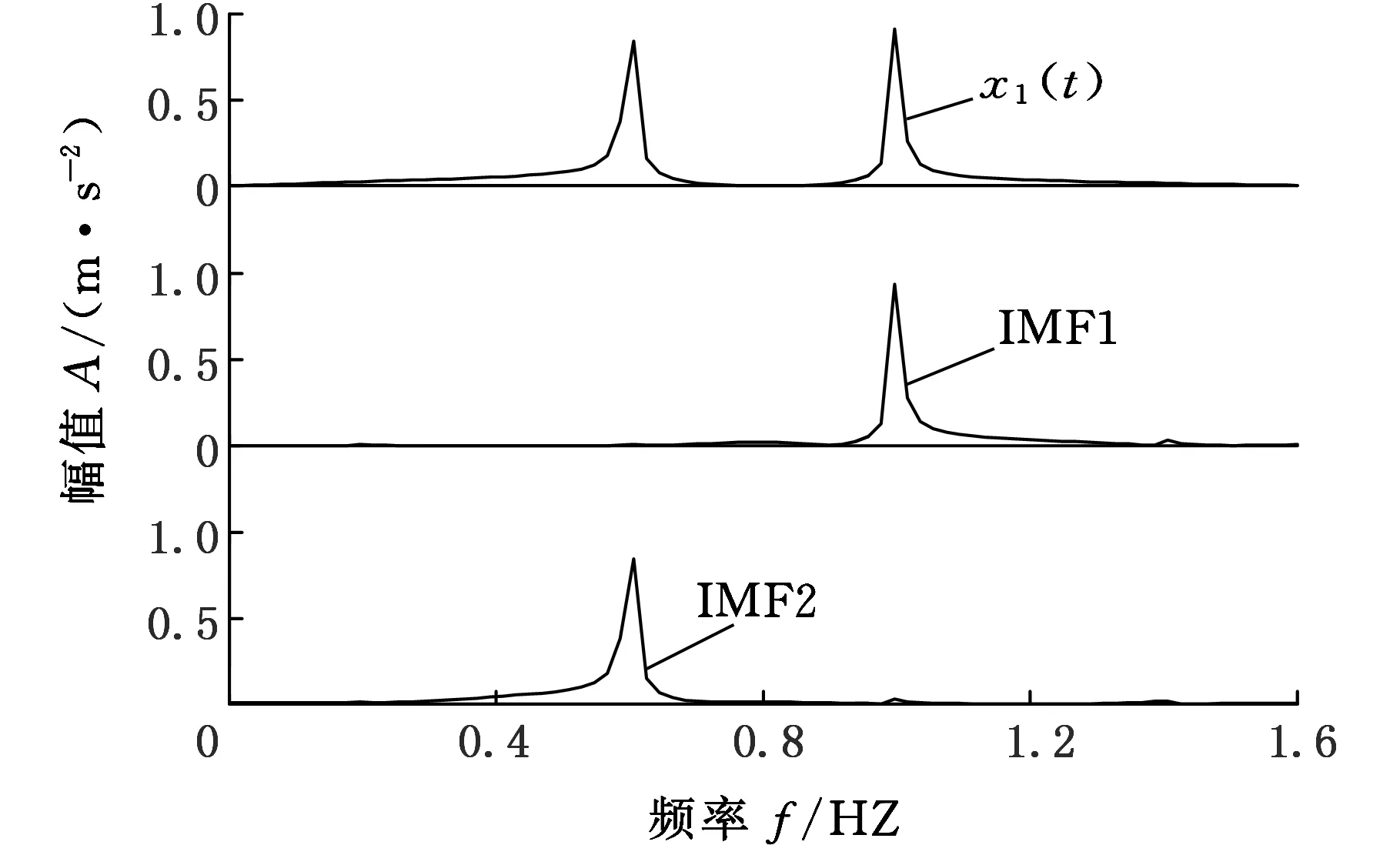
图2 x1(t)的ESMD分解Fig.2 ESMD of x1(t)

为了综合对比EMD、MEMD和ESMD的效果，取信号：

x2(t)=sin(2πf1fsn)+sin(2πf2fsn)

(9)

其中,fs=1024 Hz，f1=177.6 Hz，f2=100 Hz。信号经EMD、MEMD和ESMD处理结果如图3所示。

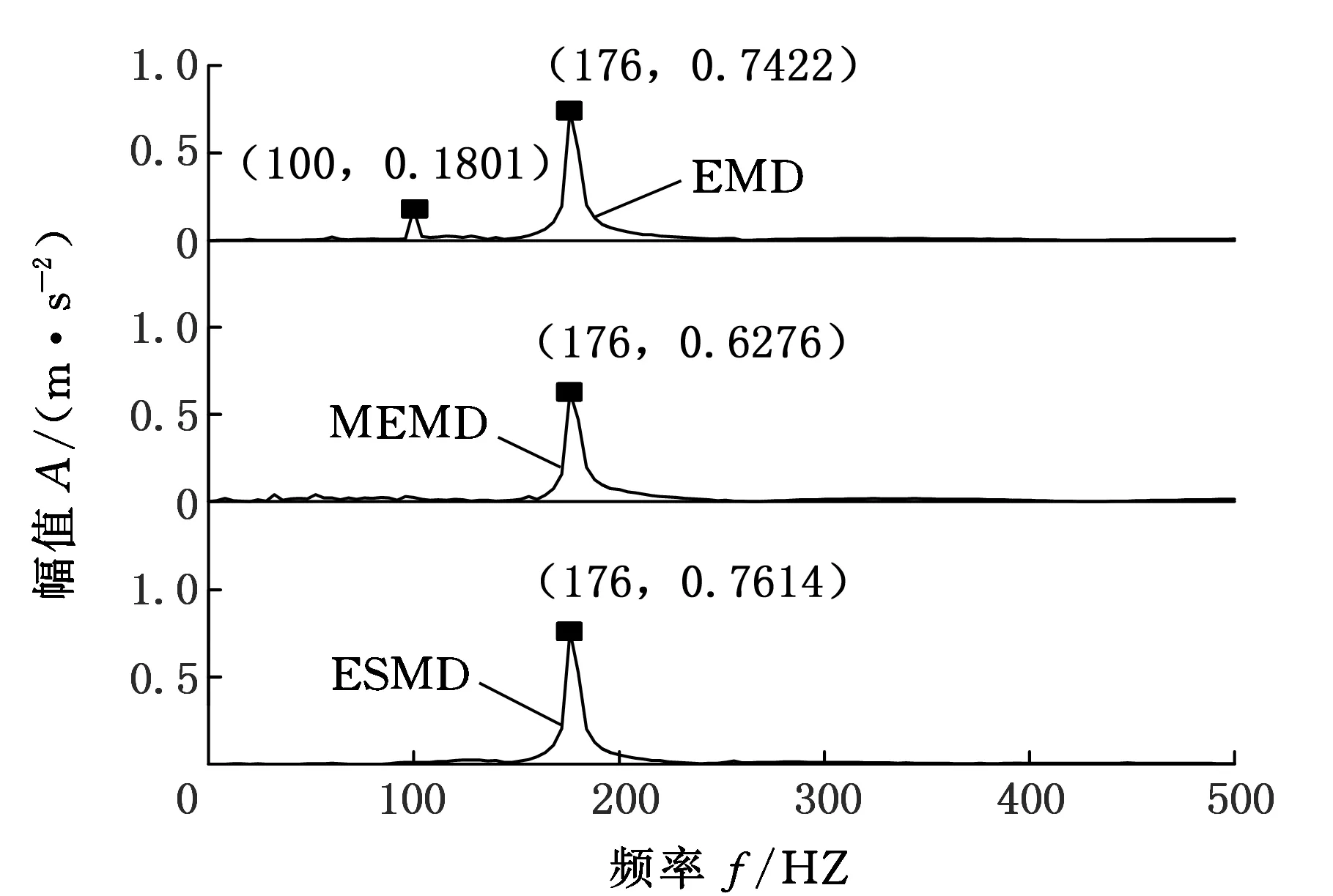
图3 x2(t)的EMD、MEMD、ESMD对比Fig.3 Comparison among EMD, MEMD and ESMDof x2(t)

由图3三种方法的对比可以看出，MEMD由于掩蔽信号的加入，在分解后会出现信号的失真，造成物理意义上的分解错误，显然ESMD分解方法很好地解决了模态混叠问题。

2 概率神经网络

典型的PNN神经网络如图4所示。它一般包括4个组成部分，即输入层、模式层、叠加层和输出层。输入层是第一层神经元。每个输入神经元在训练/测试数据集代表一个单独的属性，输入的数目与数据集中的属性数相等。输入数据的值乘以适当的权重，并被传送到模式层。输出层通常只包含一个类的最后一层，因为通常只有一个输出被要求。在训练阶段，目标是确定最准确的权重分配给连接线。在这个阶段，输出被反复计算，并与训练/测试数据集所产生的优选输出的结果进行比较[13-15]。

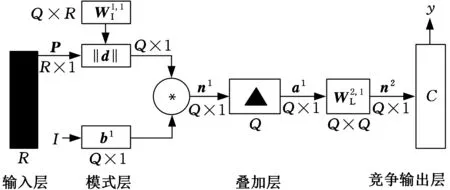
图4 概率神经网络图Fig.4 Schematic of probabilistic neural network

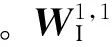
(10)

(11)

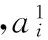
PNN具有如下优良特性: ①网络学习训练的过程简单，能较快地达到训练标准；②PNN神经网络对数据的分类准确，只要训练样本足够大，可以达到非常准确的分类效果，并且噪声对其分类效果影响低；③PNN可以用线性计算方法计算非线性数据，并能够以任意精度逼近[16]。

3 采用ESMD和PNN的轴承故障诊断流程

(1)对振动信号进行ESMD分解。

(2)分别将得到的IMF分量与原信号的相关系数进行计算并排序，取前n个IMF分量用来表征振动信号(n的取值根据具体的振动信号分解而定)。相关表达式如下：

D(X)=E(X-E(X))2

(12)

cov(X,Y)=E((X-E(X))(Y-E(Y)))

(13)

(14)

式中，D(X)为信号X的标准差;E(X)为信号X的均值;cov(X,Y)为信号X和信号Y的协方差;ρXY为信号X和信号Y的相关性系数。

(3)为了便于对数据进行PNN训练和分类，将上述所得相关性大的IMF分量进行能量的计算[17]:

(15)

i=1,2,…,n

构造出向量T，并对所得向量T进行整体归一化处理：

T=(E1,E2,…,En)

(16)

(17)

(18)

向量T′即为归一化后的能量特征向量。

(4)将T′作为特征向量输入到PNN中进行训练。

4 故障诊断实例

本实验采用美国凯斯西储大学(Case Western Reserve University)的滚动轴承故障数据。实验装置如图5所示，主要以SKF6205型深沟球轴承数据为仿真数据。

图5 轴承故障诊断实验仪器Fig.5 Experimental instrument of bearingfault diagnosis

实验中，分别随机选取风扇端以采样频率12 kHz采集滚动轴承的正常、滚动体故障、外圈故障和内圈故障4种类型的故障信号共240组，每组选取1500个点。240组数据中，200组数据作为训练样本，40组作为测试样本。

首先对上述4种轴承振动数据进行ESMD分解，并计算分解后的包含各个单主频的固有模态函数与信号的相关系数，根据相关系数选取了7组经ESMD处理过的内蕴模态函数作为PNN神经网络训练的特征分量。然后对这些特征分量进行整体归一化，分别标记滚动轴承正常、滚动体故障、外圈故障和内圈故障4种类型的故障数据为1、2、3、4，然后输入到PNN神经网络中进行分类器的分类。ESMD分解振动信号如图6所示。

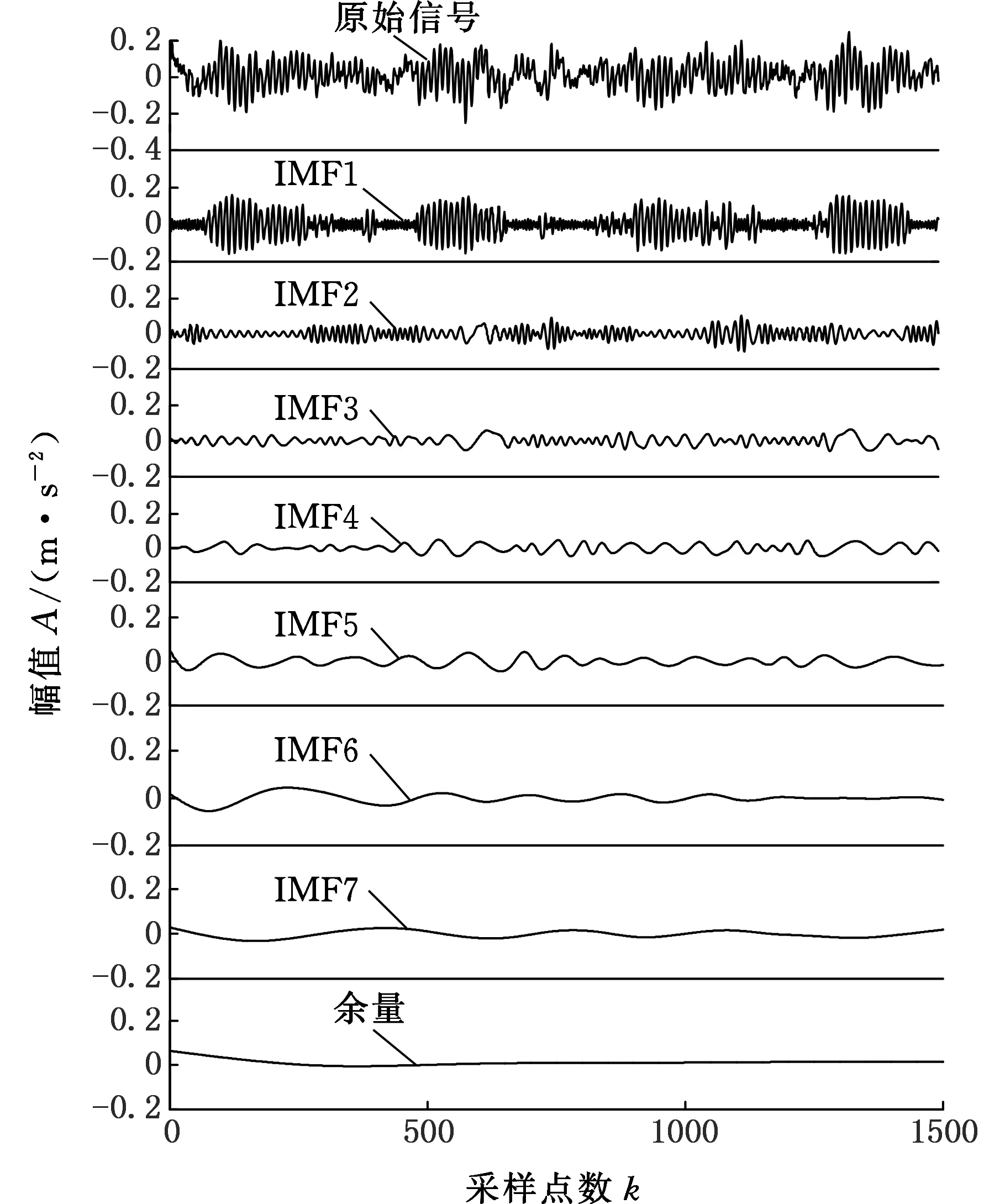
图6 ESMD分解振动信号Fig.6 The experimental results after ESMD

PNN神经网络训练中初始的SPREAD系数ηS=1。随着SPREAD系数的逐渐减小，训练效果会逐步变好。当ηS=0.1时，PNN神经网络训练结果见图7。当ηS=0.08时，PNN神经网络训练结果见图8。从图中可知，实验结果达到了预期效果。

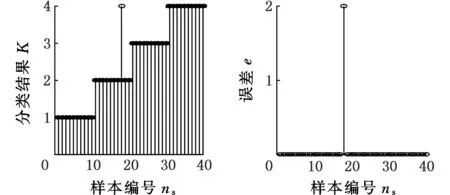
(a)PNN训练后的效果 (b)PNN训练后的误差图7 ηS=0.1时ESMD分解后PNN训练结果Fig.7 The result of using ESMD and PNN to diagnosis the rolling bearing fault under ηS=0.1

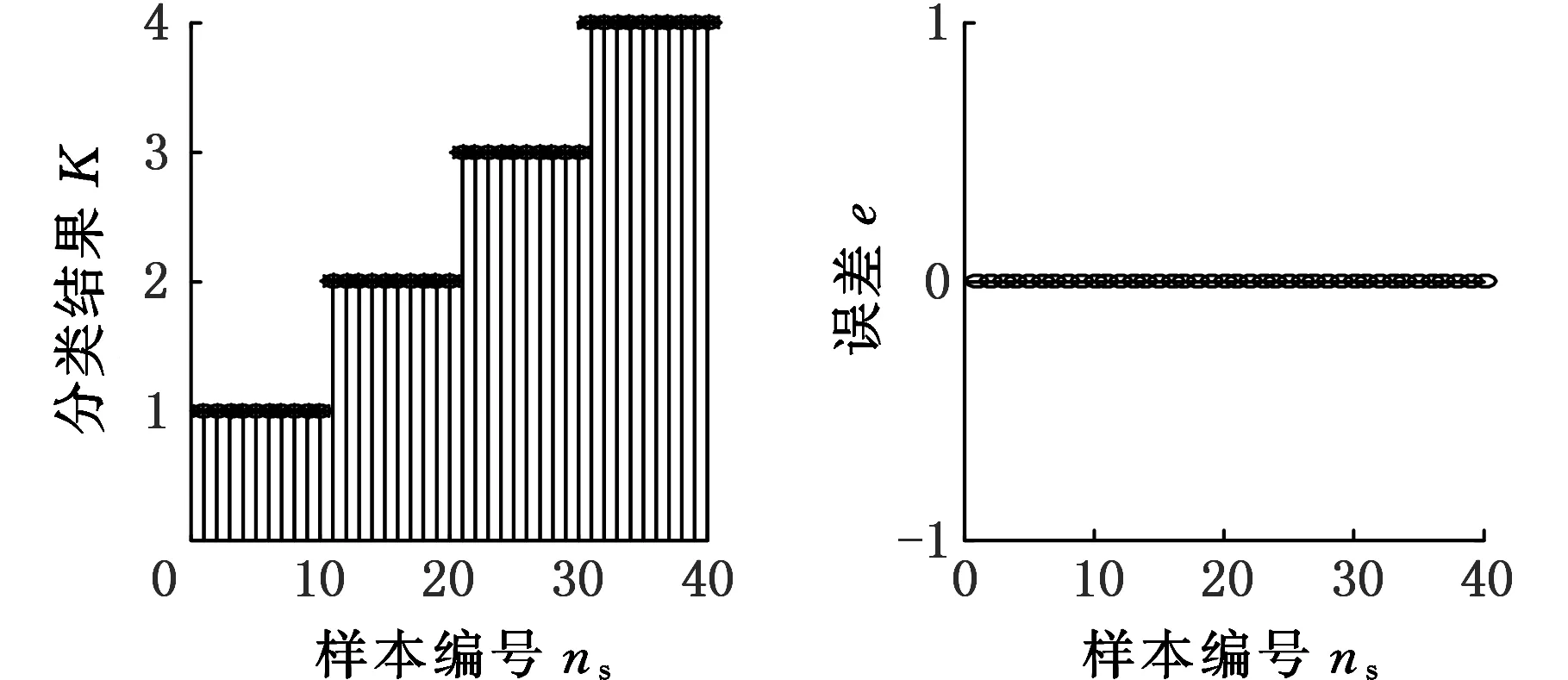
(a)PNN训练后的效果 (b)PNN训练后的误差图8 ηS=0.08时ESMD分解后PNN训练结果Fig.8 The result of using ESMD and PNN to diagnosis the rolling bearing fault under ηS=0.08

为了说明本文方法的优越性，同样信号采用EMD分解、MEMD分解和PNN训练，PNN训练结果如图9～图12所示。

图9和图10所示均为在信号分解的方法中采用了EMD后的效果。与图7、图8对比可以明显看出，ESMD方法处理过的数据相对于EMD处理过的数据在初始条件和变化条件下，数据的收敛状态与速度都要好很多。

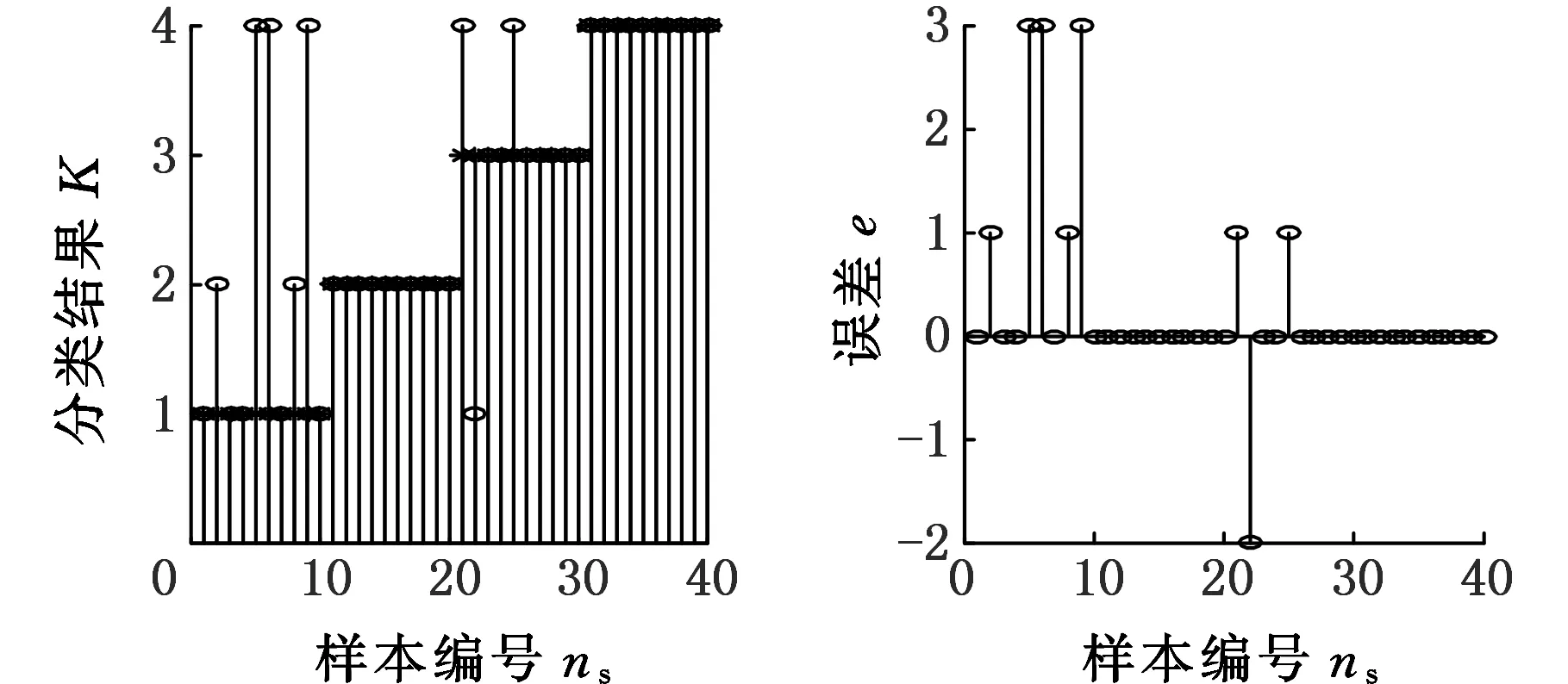
(a)PNN训练后的效果 (b)PNN训练后的误差图9 ηS=0.1时EMD分解后PNN训练结果Fig.9 The result of using EMD and PNN to diagnosis the rolling bearing fault under ηS=0.1

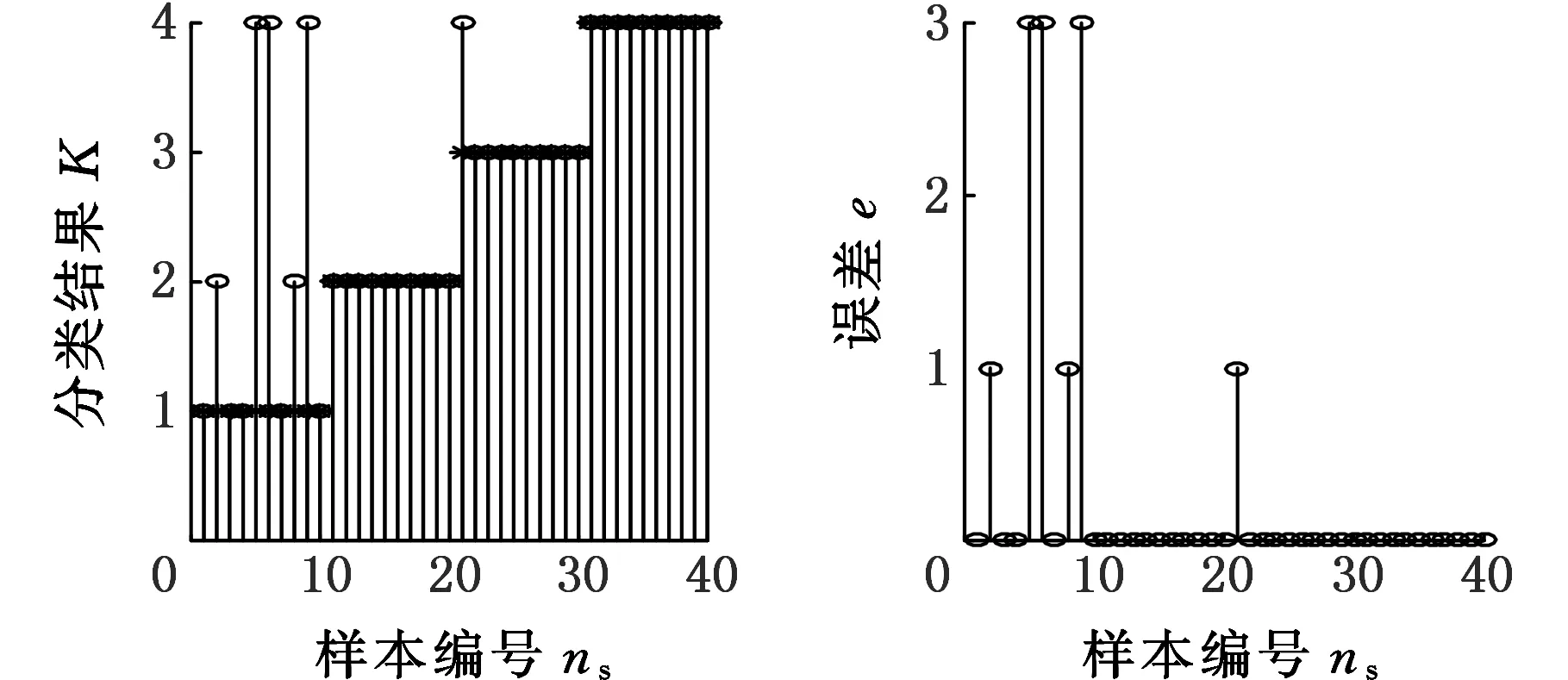
(a)PNN训练后的效果 (b)PNN训练后的误差图10 ηS=0.08时EMD分解后PNN训练结果Fig.10 The result of using EMD and PNN to diagnosis the rolling bearing fault under ηS=0.08

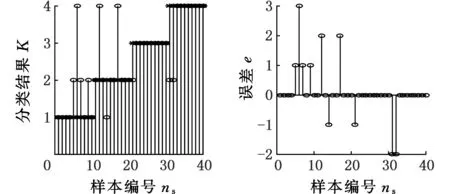
(a)PNN训练后的效果 (b)PNN训练后的误差图11 ηS=0.1时MEMD分解后PNN训练结果Fig.11 The result of using MEMD and PNN to diagnosis the rolling bearing fault under ηS=0.1

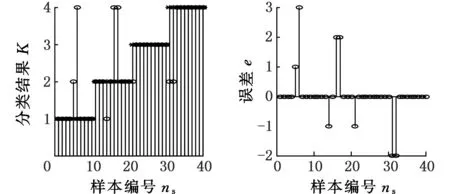
(a)PNN训练后的效果 (b)PNN训练后的误差图12 ηS=0.08时MEMD分解后PNN训练结果Fig.12 The result of using MEMD and PNN todiagnosis the rolling bearing fault under ηS=0.08

图11与图12所示均为在信号分解的方法中采用了MEMD后的效果。与图9、图10对比发现，MEMD处理信号后经PNN训练效果要好于EMD方法，在信号的初始条件以及变化条件下，其收敛速度都要高于EMD方法。但是与图7、图8相比，ESMD对信号的处理优于MEMD方法。

由上述分析可知，随着SPREAD系数的逐渐减小，经ESMD分解的信号收敛较快，分类结果准确、误差小，证明了ESMD方法的优越性。

5 结束语

本文通过极点模态分解将机械振动信号分解成多个IMF函数，以IMF分量作为信号的特征向量，采用概率神经网络对样本数据进行训练，对测试数据进行辨识，构成了旋转机械故障诊断的新方法。通过实验证明该方法可以有效地区分滚动轴承的正常、内圈、外圈、滚动体故障等故障状态，与传统的经验模态分解等方法相比，在提取信号的特征向量方面具有分解彻底、残余量可以表征信号振动趋势等优点，便于在故障初期发现故障并及时消除。实验结果表明，采用ESMD和PNN相结合的方法能够更有效地对不同故障类型信号进行诊断与识别。

[1]LIYongbo,XUMinqiang,WANGRixin,etal.AFaultDiagnosisSchemeforRollingBearingBasedonLocalMeanDecompositionandImprovedMultiscaleFuzzyEntropy[J].JournalofSoundandVibration, 2016,360:277-299.

[2] 赵志宏. 基于振动信号的机械故障特征提取与诊断研究[D]. 北京：北京交通大学，2012.ZHAOZhihong.ResearchonVibrationSignalBasedMachineryFaultFeatureExtractionandDiagnosis[D].Beijing:BeijingJiaotongUniversity, 2012.

[3] 钟先友. 旋转机械故障诊断的时频分析方法及其应用研究[D]. 武汉：武汉科技大学, 2014.ZHONGXianyou.ResearchonTime-frequencyAnalysisMethodsandItsApplicationstoRotatingMachineryFaultDiagnosis[D].Wuhan:WuhanUniversityofScienceandTechnology, 2014.

[4]GILLESJ.EmpiricalWaveletTransform[J].IEEETransactionsonSignalProcessing, 2013, 61(16): 3999-4010.

[5] 黄建，胡晓光，巩玉楠.基于经验模态分解的高压断路器机械故障诊断方法[J]. 中国电机工程学报，2011，31(12):108-113.HUANGJian,HUXiaoguang,GONGYunan.MachineryFaultDiagnosisofHighVoltageCircuitBreakerBasedonEmpiricalModeDecomposition[J].ProceedingsoftheCSEE, 2011，31(12):108-113.

[6] 时培明, 李庚, 韩东颖. 基于改进EMD的旋转机械耦合故障诊断方法研究[J].中国机械工程, 2013, 24(17): 2367-2372.SHIPeiming,LIGeng,HANDongying.StudyonCouplingFaultsofRotaryMachineryDiagnosisMethodBasedonImprovedEMD[J].ChinaMechanicalEngineering, 2013, 24(17): 2367-2372.

[7]DEERINGR,KAISERJF.TheUseofaMaskingSignaltoImproveEmpiricalModeDecomposition[C]//Acoustics,Speech,andSignalProcessing, 2005.Pennsylvania, 2005: 485-488.

[8] 全学海, 丁宣浩, 蒋英春. 基于EMD和概率神经网络的说话人识别[J]. 桂林电子科技大学学报, 2012, 30(2): 108-112.QUANXuehai,DINGXuanhao,JIANGYingchun.SpeakerRecognitionBasedonEMDandProbabilisticNeuralNetworks[J].JournalofGuilinUniversityofElectronicTechnology, 2012,30(2): 108-112.

[9]WANGJinliang,LIZongjun.Extreme-pointSymmetricModeDecompositionMethodforDataAnalysis[J].AdvancesinAdaptiveDataAnalysis, 2013,5(3):1350015.

[10]LIHuifeng,WANGJinliang,LIZongjun.ApplicationofESMDMethodtoAir-seaFluxInvestigation[J].InternationalJournalofGeosciences, 2013, 4(5): 8-11.

[11] 王金良, 李宗军. 可用于气候数据分析的ESMD方法[J]. 气候变化研究快报, 2014(3): 1-5.WANGJinliang,LIZongjun.TheESMDMethodforClimateDataAnalysis[J].ClimateChangeResearchLetters, 2014(3): 1-5.

[12] 包红燕. 基于MEMD和条件熵相空间重构的滚动轴承故障诊断[D]. 秦皇岛：燕山大学, 2014.BAOHongyan.RollingBearingFaultDiagnosisBasedonMaskingEmpiricalModeDecompositionandPhaseSpaceReconstructionofConditionalEntroy[D].Qinhuangdao：YanshanUniversity, 2014.

[13]CHENXianyue,ZHOUJianzhong,XIAOHan.FaultDiagnosisBasedonComprehensiveGeometricCharacteristicandProbabilityNeuralNetwork[J].AppliedMathematicsandComputation, 2014, 230(3) : 542-554.

[14]WANGChangqing,ZHOUJianzhong,QINGHui.FaultDiagnosisBasedonPulseCoupledNeuralNetworkandProbabilityNeuralNetwork[J].ExpertSystemswithApplications, 2011, 38 (11):14207-14313.

[15] 刘凤龙, 宋艺. 基于EMD与PNN的机械故障检测[J]. 计算机应用与软件, 2010, 27(9): 237-239.LIUFenglong,SONGYi.MachineryFaultDiagnosisBasedonEMDandPNN[J].ComputerApplicationsandSoftware, 2010,27(9): 237-239.

[16] 孟宗，胡猛，谷伟明,等. 基于LMD多尺度熵和概率神经网络的滚动轴承故障诊断方法[J]. 中国机械工程, 2016, 27(4): 433-437.MENGZong,HUMeng,GUWeiming,etal.RollingBearingFaultDiagnosisMethodBasedonLMDMulti-scaleEntropyandProbabilisticNeuralNetwork[J].ChinaMechanicalEngineering, 2016,27(4): 433-437.

[17] 肖韬，袁兴中，唐清华,等. 基于概率神经网络的城市湖泊生态系统健康评价研究[J]. 环境科学学报, 2013, 33(11): 3166-3172.XIAOTao,YUANXingzhong,TANGQinghua,etal.InvestigationofHealthAssessmentforUrbanLakesSystemBasedonProbabilisticNeuralNetworks[J].ActaScientiaeCircumstantiae, 2013, 33(11): 3166-3172.

(编辑 王旻玥)

Fault Diagnosis of Bearings Based on Extreme-point Symmetric Mode Decomposition and Probabilistic Neural Network

ZHANG Shuqing1XU Jiantao1JIANG Anqi2LI Junfeng1SU Xinshuang1JIANG Wanlu3

1.Institute of Electrical Engineering,Yanshan University,Qinhuangdao,Hebei，066004 2.School of Information Engineering,Central South University,Changsha,410006 3.College of Mechanical Engineering,Yanshan University,Qinhuangdao,Hebei，066004

Aimed at the complex non-linear rolling bearing systems, a new method combining ESMD and PNN was introduced for bearing fault diagnosis. ESMD expanded the definition of the intrinsic mode function, and changed the external envelope interpolation to internal pole symmetric interpolation. An idea of adaptive global mean(AGM) was used to optimize the last remaining modal, thus to determine the optimal number of decomposition. PNN was a neural network classifier based on kernel function approximation. The exponential functions were introduced to the neural network to replace the S type activation functions and to reconstruct the functions, representing the notion of gradient steepest descent method prominently, and reducing the errors between the actual and predicted output functions. Through the decomposing comparison to the simulation signals among empirical mode decomposition(EMD), making empirical mode decomposition(MEMD) and ESMD, and the diagnosis to the bearing vibration data by ESMD and PNN shows that the new method introduced may diagnose the bearing faults more effectively.

rolling bearing; extreme-point symmetric mode decomposition(ESMD); probabilistic neural network(PNN); fault diagnosis

2016-04-01

国家自然科学基金资助项目(51475405，61077071)；河北省自然科学基金资助项目(F2016203496,F2015203413)

TH17

10.3969/j.issn.1004-132X.2017.04.009

张淑清，女，1966年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为弱信号检测、智能信号处理、故障诊断。发表论文50余篇。E-mail:zhshq-yd@163.com。 徐剑涛，男，1992年生。燕山大学电气工程学院硕士研究生。姜安琦，女，1995年生。中南大学信息科学与工程学院本科生。李军峰，男，1994年生。燕山大学电气工程学院硕士研究生。宿新爽，女，1993年生。燕山大学电气工程学院硕士研究生。姜万录，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。