模具圆心角对AZ31镁合金剧烈塑性变形的影响
刘婷++卢寿丽

【摘 要】模具圆心角对ECAP工艺过程有显著的影响。本文通过有限元模拟软件Deform-2D进行了大量的数值模拟,研究了模具圆心角对试样变形分布的影响。分析结果表明, 当模具圆心角为30°时,工件的等效应变分布更加合理,这些结果为优化模具结构,获得性能优良的镁合金提供了有效可靠的指导。
【关键词】等通道转角挤压变形;有限元模拟;模具圆心角
1.引言
ECAP是由两个横截面积相同的通道相交而成,其中内交角用Φ来表示,外交角Ψ用来表示。它具有不改变材料横截面积和横截面形状的特点,在挤压过程中,材料经过多次剪切变形后累积较大的变形量,从而使晶粒细化到微米、亚微米和纳米级尺寸.当忽略边界条件如摩擦等的作用是,Iwahashi[1]等人通过纯剪切几何变换法推导得出等通道弯角挤压变形过程的等效应变累积公式(1),由此公式可以看出,等通道转角挤压变形,可以通过多道次挤压来累积足够的应变量以达到细化晶粒的目的。
(1)
公式中,N是挤压道次数,是累积等效应变,随模具拐角Φ和模具圆心角Ψ的增大而减少。由公式可以看出,当Φ=90°,Ψ=0°时,为最大值1.15,当Φ=90°,Ψ=90°时,为最小值0.907。
虽然科研人员对等通道转角挤压进行了大量的研究,但研究对象主要集中在铜[2,3]、铝、钛及其合金上,很少有对镁及镁合金的研究。镁及镁合金是密排六方结构,在室温下无法获得较高的塑性,但经等通道弯角挤压工艺后,镁及镁合金的晶粒的到了明显的细化,性能也得到了改善。
本文的主要目的是通过有限元模拟软件Deform-2D对镁合金AZ31的ECAP过程进行数值模拟,分析在不同模具圆心角下,镁合金剧烈塑性变形的变形机理,为获得合理的模具结构,挤压出性能良好的镁合金,为ECAP实验进行理论指导。
2.有限元数值模拟
本文采用方形等通道转角挤压模具对镁合金AZ31的ECAP工艺进行大量的数值模拟,研究不同的工艺参数对试样变形分布的影响。在模拟过程中,挤压过程为平面变形问题,假设模具为刚性,材料为刚塑性,且在常温下符合应力应变关系[4],其中C=205MPa,应变硬化指数m=0.114,n=0.044, 模具拐角90°,摩擦因子0.15,挤压件的几何形状为12mm×12mm×60mm, 網格单元划分数是800。
模拟过程中的参数变化: 模具圆心角Ψ分别取0°、30°、60°和90°三种情况。此外,截取挤压件的横截面进行分析,要获得挤压件挤压过程中各场量的演化规律,取初始时挤压件中心处5个点进行分析. 观察不同参数下试样的变形分布等情况.总结AZ31的等通道转角挤压的规律。
3.模拟结果与分析
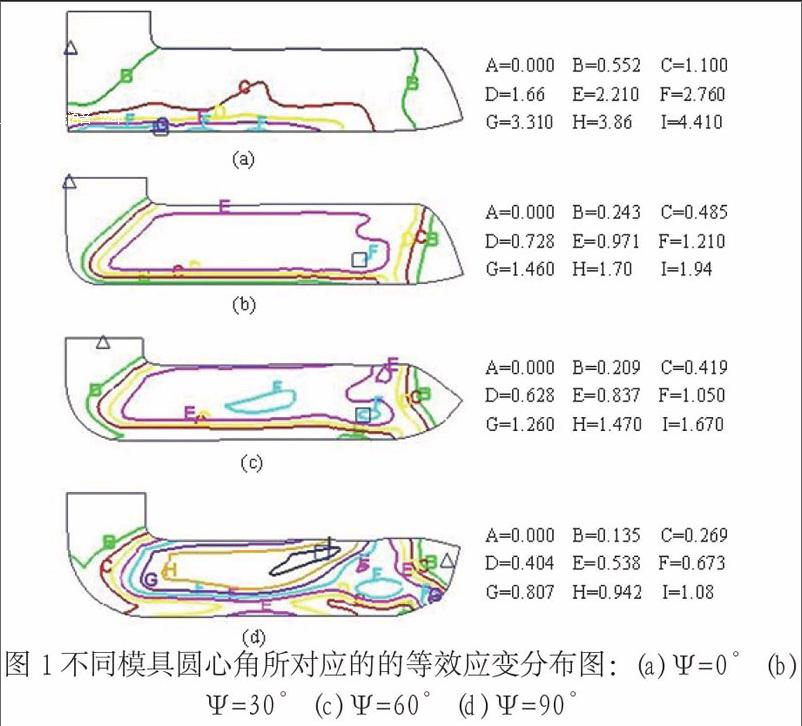
图1不同模具圆心角所对应的的等效应变分布图:(a) Ψ=0°(b) Ψ=30°(c) Ψ=60° (d) Ψ=90°
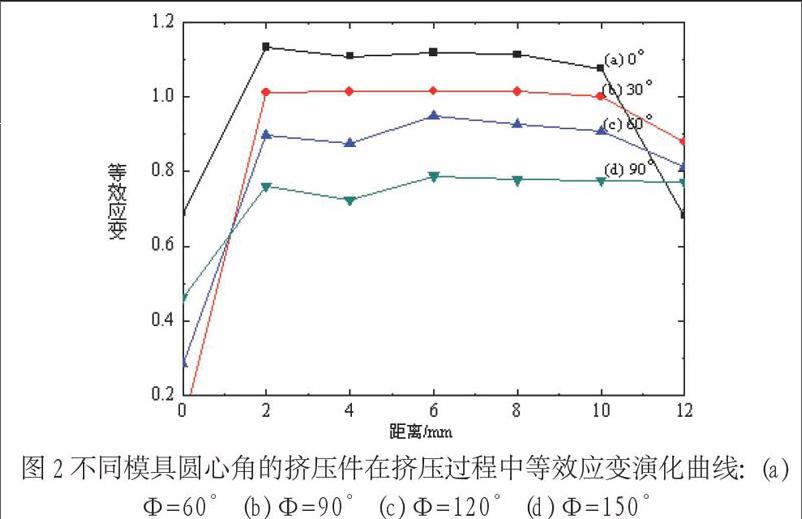
图1中(a)、(b)、(c)、(d)分别表示模具拐角为90°时,模具圆心角分别为0°、30°、60°、90°时,工件的等效应变分布图。由图可知,随着模具圆心角的增大,工件最大等效应变值与最小等效应变值在减小 ,但变形的均匀化程度不同,基本上呈现(b)>(c)>(a)>(d)的情况,模具拐角是90°,模具圆心角是30°时,工件变形优于其他条件。由于ECAP工艺属于剧烈塑性变形,所以选择圆心角时,变形对模具的影响不可忽略,综合考虑各种条件和模拟结果,模具圆心角选在30°附近较为合理。图2表示模具拐角为90°时,模具圆心角分别为0°、30°、60°、90°时,挤压件A-B处各点的等效应变演化曲线。从图中可以看出在试样的第二部分等效应变随模具圆心角的增大而减小。模具圆心角越小,等效应变越均匀。
图2不同模具圆心角的挤压件在挤压过程中等效应变演化曲线:(a) Φ=60°(b) Φ=90°(c) Φ=120°(d) Φ=150°
4.结论
通过有限元软件De-form2D模拟了镁合金AZ31的ECAP变形过程,分析了模具圆心角对变形过程的影响,为优化模拟,获得性能良好的工件提供了可靠有效的理论指导:模具圆心角增大,工件的等效应变是在减小的,当模具圆心角为30°时,工件的变形是更为均匀的。
参考文献:
[1]IWAHASHI Y, ORITA H Z, NEMOTO M, et al. An investigation of
microstructural EV olution during equa-lchannel angular pressing[J]. ACTA Mater, 1997, 45(11): 4733-4741.
[2]DAN Song, MA Bin-ai, JIANG Hua-jing, et al. Corrosion behavior of ultra-fine grained industrial pure AL fabricated by ECAP[J]. Transactions of Nonferrous Metals Society of China, 2009, 19(5): 1065-1070.
[3]STOLYAROV V V, ZHU Y-t, RAAB G I, et al. Effect of initial microstructure on the microstructural evolution and mechanical properties of TI during cold rolling[J]. Materials Science and Engineering: a, 2004, 380(1/2): 309-313.
[4]ALTAN T, L S O, GEGEL L H, et al. Metal forming fundamentals and applications[M]. American: ASFM, 1983: 59-71.

