联合FCM与群集蜘蛛优化SVR的短时交通流量预测

曹成涛，林晓辉，许伦辉

(1.广东交通职业技术学院 智能交通工程技术应用中心，广东广州 510650;2. 华南理工大学，广东广州 510640)

联合FCM与群集蜘蛛优化SVR的短时交通流量预测

曹成涛1，林晓辉1，许伦辉2

(1.广东交通职业技术学院 智能交通工程技术应用中心，广东广州 510650;2. 华南理工大学，广东广州 510640)

对智能交通系统(ITS)短时交通流量预测问题进行研究，提出了一种联合FCM与群集蜘蛛优化SVR交通流量预测算法。首先采用FCM聚类方法对交通流量数据预处理，得到基于时间节点分割的时序数据模块，有效降低了数据差异性带来的误差影响；然后构建基于群集蜘蛛优化SVR模型，针对SVR参数选择难题，在群集蜘蛛优化算法中引入社会等级制度，动态的将蜘蛛种群划分为上中下三个阶层，并根据不同阶层个体适应度大小，分别设计自适应竞争、"快搜"以及逆向学习机制，提高了算法寻优精度；最后，运用群集蜘蛛优化SVR对各个交通流量数据时序模块进行预测评估。仿真结果表明，同其它预测算法相比，该算法预测平均绝对误差降低了38.4～53.8%。

交通流量预测；模糊C-均值聚类；支持向量回归(SVR)；群集蜘蛛优化

0 引 言

短期交通流量预测作为智能控制与信息管理的基础[1]，其在智能交通系统(Intelligent Transportation System，ITS)中有着广泛的应用，实时、准确的交通流量预测信息能够有效缓解交通拥堵，降低能源消耗以及减少交通事故[2,3]。由于道路交通量变化具有非平稳、非线性等特点，交通流量数据呈现出不确定性和随机性[4]，因此，短时交通流量预测研究已成为城市智能交通系统关键问题之一。

短时交通流量预测方法可以分为经典数理分析、非线性系统理论和人工智能模型三类[5]，面对道路交通实时变化、非平稳随机过程，神经网络[6]、支持向量机(SVM)[1]、极端学习机(ELM)[2,5]等智能预测模型展现出了优越性能，但是受数据特征和适用条件限制，不存在一种预测方法能够在任何状况下都能保持绝对好的预测性能[7,15]，为此，学者们围绕扩大预测适用范围和提高预测精度展开了深入研究：董春娇等[3]结合流量数据时空特性，构建了自由流状态下的短时预测模型，实现了道路交通流状态准确预判，但是没有充分考虑三种交通流态相互转化对预测精度的影响；董宏辉等[8]针对交通状态多模态特点，提出了一种多模态交通流量预测方法，通过研究流量数据与不同模态之间的对应关系，在优化ARIMA模型的基础上得到了较高预测精度的交通流量预测结果，但是该方法对数据平稳性要求较高；文献[9]提出了一种基于频谱分析的实时更新短时交通流预测算法，仿真实验也验证了该算法的有效性；商强等[5]在相空间重构交通流量时序的基础上，构建了基于正则化ELM的短时交通流量预测模型，有效提高了预测精度，但是原始系统与重构相空间一致性程度有待进一步研究；芮兰兰等[2]将K-means聚类方法应用于交通流量时序分割，并运用ELM模型对各个时序块进行预测，仿真结果证明该方法具有更高的可信度，但是该算法没有充分考虑ELM过拟合缺陷带来的影响。

大量研究表明支持向量回归(SVR)能够有效处理小样本、高维非线性预测问题，并在模式识别[10]、参数估计[11]、故障预判等领域[12]得到了广泛应用，但是SVR参数配置问题至今仍没有得到很好的解决[1]。为了降低交通流量数据差异性、随机性带来的误差影响，提高SVR模型预测精度，本文提出一种联合FCM与群集蜘蛛优化[13]SVR交通流量预测算法，通过流量时序数据模块划分、群集蜘蛛优化SVR模型参数以及时序数据模块预测评估实现对短时交通流量的可靠预测，实测数据与模型预测对比实验验证了该算法的有效性。

1 问题描述与FCM聚类分析

交通流量数据具有明显的时序特性，因此，时序模型是短时交通流量预测主要模型之一[14]。交通控制周期通常为2.5～3.0 min，而交通诱导周期通常为5 min[5]，因此，设定数据样本采集和预测时间间隔ΔT=5 min。

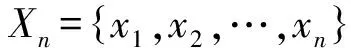
定义2 交通流量预测。对于观察时刻t和流量预测模型，利用前τ个时刻流量对t时刻流量xt进行预测：

(1)

其中，τ为为嵌入维数。

(2)

(3)

(4)

其中，输入变量xi∈Rn，输出变量yi∈R。

观察时间序列Xn，不难发现通常某个时间段内流量数据具有更多相似性[16]，例如上班早高峰时间段，交通流量数据明显高于非高峰时期，为了降低不同时间段交通流量数据差异性、随机性带来的误差影响，采用FCM聚类方法对Xn进行时序数据模块划分，从而得到多个流量数据时间序列。基于FCM时序数据模块划分过程为：

Step1.初始化。设置聚类簇集个数K、模糊加权指数M、最大迭代次数Tmax以及终止条件Θ。随机生成K个聚类簇集中心vk(k=1,2,…,K)。

Step2.隶属度矩阵计算。对于xi，根据式(5)计算其对vk的隶属度值μki。

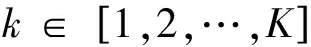
(5)

Step3.聚类中心计算。根据式(6)重新计算聚类中心vk。

(6)

Step5.时序调整。对于第k个聚类簇集，由于FCM基于交通流量值大小进行聚类分析，因此，其内部元素对应的采集时间可能是不连续的，需要依次对聚类簇集进行时序调整：保留簇集内采集时间连续变化最多的元素，并将剩余元素剔除；当所有簇集完成对应操作后，按照时序空缺，依次将剔除元素加入与之对应的空缺时序簇集内，如果某个剔除元素能够同时进入两个聚类簇集，则优先选取距离聚类中心较近的簇集。

定义4 时序数据模块分割。时间序列Xn执行FCM时序数据模块划分操作后，得到多个时序数据模块：

(7)

2 支持向量回归(SVR)

支持向量机(SVR)本质是通过非线性映射φ(x)将低维数据x映射到高维特征空间，并完成线性回归拟合，即：

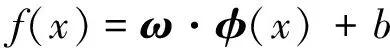
(8)

其中，向量ω∈。当样本不满足拟合函数时，引入损失函数参数ε、松弛变量和惩罚系数C，并将线性回归拟合转化为约束优化问题，即：

(9)

其中，l为样本数。在式(9)中引入拉格朗日函数、对偶变量以及核函数：

(10)

根据KKT条件有：

(11)

此时，式(9)转化为：

(12)

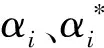
(13)

结合定义2、定义3，对于利用前τ个时刻流量对t时刻流量进行预测问题，其拟合函数为：

(14)

其中，t=τ+1,…,n。本文选取核函数为径向基核函数：

(15)

SVR存在参数选择难题，而惩罚系数C、损失函数参数ε、核函数σ以及嵌入维数τ对SVR预测结果可信度有着重要影响：①C用于平衡拟合误差与预测模型复杂度，C取值过小或者过大会产生“欠学习”或“过学习”现象。②ε用于控制拟合误差大小，ε不合理取值会增加计算量或者降低预测精度。③σ对模型预测精度影响较大。④τ决定了系统相空间重构准确度，对模型预测可信度起到决定性作用。为了获取最佳SVR模型预测性能，本文采用SSO实现SVR模型参数选取。

3 群集蜘蛛优化的SVR预测模型

3.1 基本SSO算法

SSO作为最近才被提出的智能优化算法，在经典测试函数优化问题表现出了优异性能[13]，其主要模拟蜘蛛群体协同进食现象，通过个体之间信息交流，最终寻找到优化问题最优解。SSO原理描述如下(最小值问题)：

Step1.算法初始化。对于N维优化问题，随机生成由P只蜘蛛组成的蜘蛛种群S，S又分为雌性子群F和雄性子群M，F内雌性蜘蛛数量Pf、M内雄性蜘蛛数量Pm分别为：

(16)

Step2.蜘蛛进化。SSO通过蜘蛛生物学行为，分别为雌性蜘蛛Fi、雄性蜘蛛Mi定义了不同的进化方式：

(17)

(18)

其中，J(·)为目标函数适应度值，ωi、ωNf+m分别为蜘蛛权重值和群体权重参考值；Sc为与Fi最近且权重高于Fi的蜘蛛，Sb为F中权重最高的蜘蛛，Sf为距离Mi最近蜘蛛；Vibvl为蜘蛛感知能力，PF为概率因子，α、β、rm、δ为随机数。

Step3.婚配行为。对于雄性蜘蛛Mi，当ωi>ωNf+m时，Mi每个维度以轮盘赌的方式选取婚配半径r内的雌性蜘蛛进行维度数值交换。

(19)

其中，Fjmax、Mjmax和Fjmin、Mjmin表示蜘蛛第j维最大值与最小值。

Step4.终止条件判断。重复执行蜘蛛进化和婚配行为，直至满足终止条件。

3.2 SSO改进方法

研究表明，对于复杂函数优化问题，SSO容易出现“早熟”现象，导致收敛精度不高。为了提高SSO求解复杂问题能力，从3方面进行改进：①提高蜘蛛种群多样性，根据群体内蜘蛛适应度大小，建立上中下3种社会等级；②改进蜘蛛个体更新策略，对于下层蜘蛛设计逆向学习机制；③加快算法收敛速度，对于上层蜘蛛设计“快搜”策略。(以雌性子群为例)

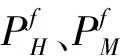
(20)

自适应竞争 在算法每次迭代结束后，适应度排名靠前的蜘蛛以自适应竞争的方式进入上层阶级，即：

(21)

逆向学习机制 对于下层阶级蜘蛛，本文模拟光学反射现象，提出逆向学习机制(如图1(a)所示)，其具体工作原理为：

(22)

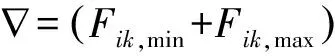
(23)

(24)

又有：

(25)

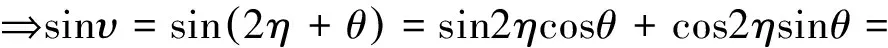
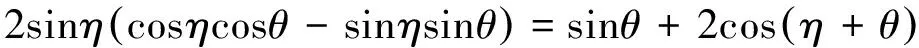
(26)

联立式(23-26)有：

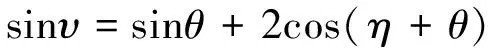
(27)

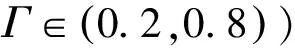
(28)

η以Δη变化率转动镜面，可以得到系列Fik,new，取适应度最优的维度值作为k维变量最终更新结果。当Fi完成所有维度更新后，若蜘蛛适应度值优于原来蜘蛛，则新的蜘蛛替代原个体；否则随机生成新的蜘蛛。

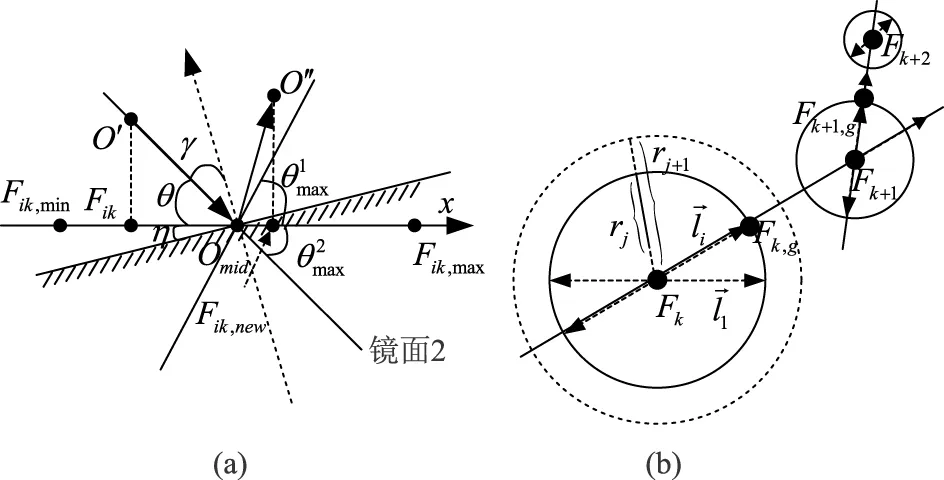
图1 逆向学习机制示意图

“快搜”策略 对于上层阶级蜘蛛，本文设计“快搜”策略，以提高算法收敛速度(如图1(b)所示)。“快搜”策略工作过程为：

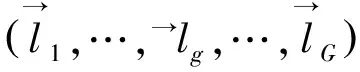
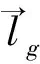
(29)

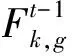
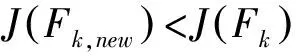
3.3 SSO-SVR实现

(30)

其中，Ci,min,Ci,max,εi,min,εi,max,σi,min,σi,max,τi,min,τi,max分别为惩罚函数C、损失函数参数ε、核函数σ以及嵌入维数τ取值范围。

定义6 目标函数。对于SVR参数配置问题，目标函数定义为：

(31)

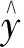
SSO-SVR实现流程为：

输入：训练样本交通流量时间序列、聚类簇集个数K和需要预测流量时间段。输出：交通流量预测值。1 根据FCM时序数据模块划分过程，得到{X′1，X′2，…，X′K}。Fork=1：Kdo//对每个时序模块预测2 算法初始化。设置SSO-SVR相关参数，读入样本数据。While(终止条件不满足)do{3 根据式(20)对种群进行阶层划分。4 根据式(28)分别对雌雄子群内下层阶级蜘蛛进行更新；根据“快搜”策略分别对雌雄子群内上层阶级蜘蛛进行更新；中层蜘蛛采用基本SSO算法更新策略。5 雌雄子群发生婚配行为。6 更新雌雄子群最优解和全局最优解。}7 得到SVR最佳参数组合Ck，best，εk，best，σk，best，τk，best()。8 根据式(14)对交通流量进行预测，得到该时段交通流量数据。Endfor

4 实验仿真

实验采用两组数据源：第1组与第2组分别采集广州市某十字路口和丁字路口7天内6:00～10:00 交通流量作为实验数据(采集时间间隔ΔT=5 min)，共得到343个数据。其中前6天数据作为训练样本，而第7天数据用于预测评估模型[17]。为了分析SSO-SVR预测性能，引入平均绝对误差MAE、均方误差RMSE和均等系数EC3个指标[18,19]。

(32)

(33)

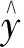
4.1 仿真结果分析

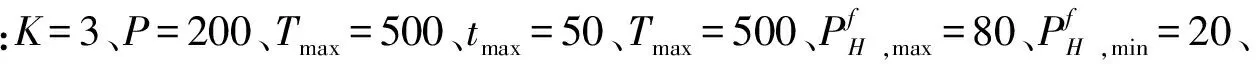
表1 预测模型参数优化结果

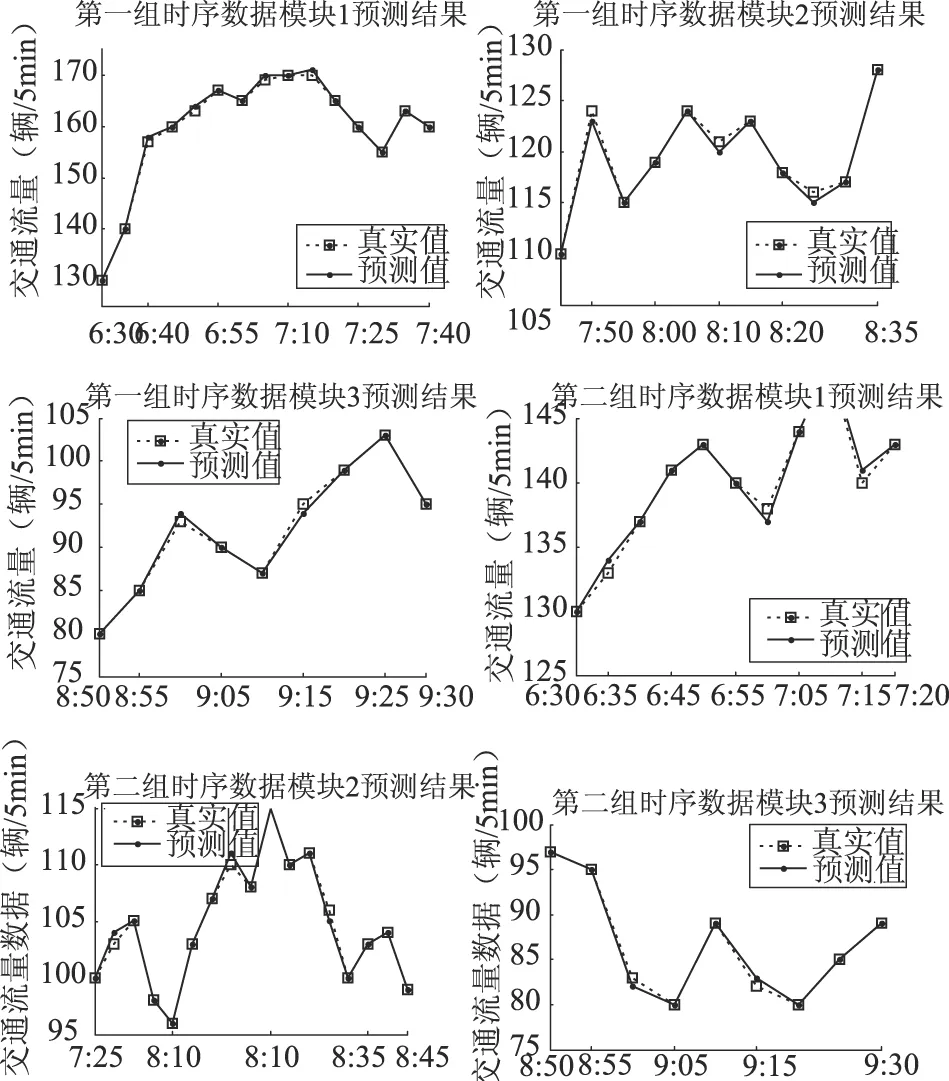
图2 SSO-SVR各个时序数据模块预测结果

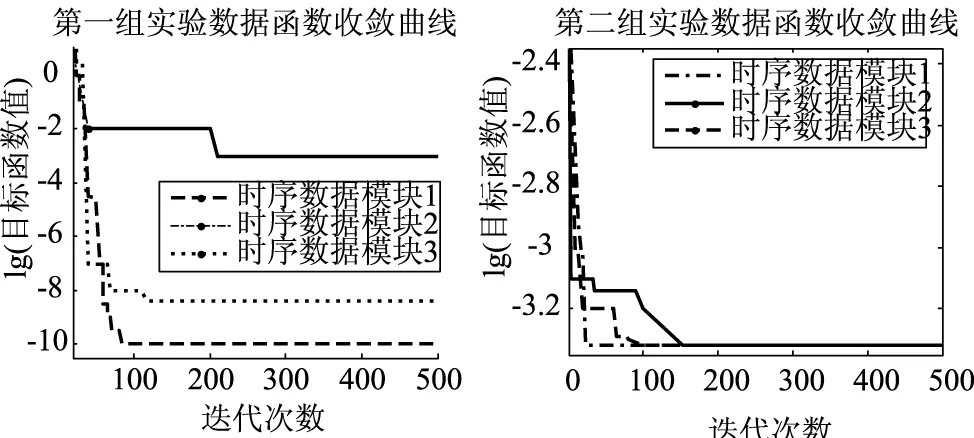
图3 SSO优化SVR参数配置函数收敛曲线

从表1和图2可以看出，SSO-SVR将流量数据分割成3个时序数据模块，而且每个模块的均等系数EC指标都在0.90以上，表明流量预测值与真实测量值拟合程度很高。从图2可以看出，SSO基本只需要180迭代就能够收敛取最优解，而且具有较高的收敛精度。

4.2 对比实验分析

为了进一步分析SSO-SVR预测模型性能，选取文献[1]提出的CPSOAFS-SVR模型和文献[2]提出的TFPBCM模型进行对比实验，其中SSO-SVR仍采取FCM聚类时序模块分割机制，当各个模块完成流量预测后，所有预测结果汇总后统一进行指标分析。图4给出了不同预测模型流量预测对比结果，表2给出了不同预测模型指标对比。

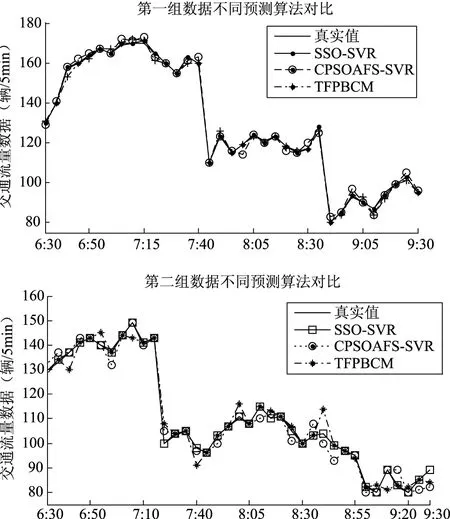
图4 不同预测模型流量预测对比

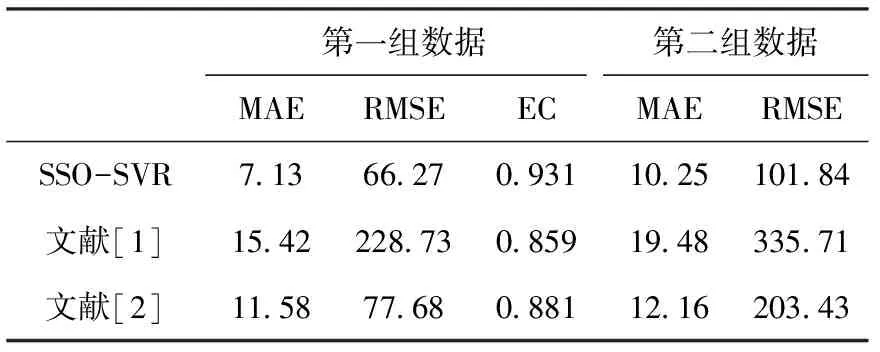
第一组数据第二组数据MAERMSEECMAERMSEECSSO-SVR7 1366 270 93110 25101 840 927文献[1]15 42228 730 85919 48335 710 889文献[2]11 5877 680 88112 16203 430 892

从图4和表2可以看出，SSO-SVR三种指标都要优于其它两种模型：对于EC指标，SSO-SVR都在0.91以上，比其它两种模型更加接近1，表明该模型预测值与真实值拟合程度更高；对于MAE和RMSE指标，SSO-SVR都要低于另外两种模型，表明该模型预测精度更高，预测平均绝对误差降低了38.4～53.8%。仿真结果表明，联合FCM与群集蜘蛛优化SVR短时交通流量预测模型在短时交通流量预测方面具有较大优势。

5 结 语

提出了一种联合FCM与群集蜘蛛优化SVR的短时交通流量预测方法，该方法在FCM时序数据模块分割的基础上，利用群集蜘蛛优化SVR模型实现对短时交通流量数据准确预测，仿真结果也验证了该方法的有效性。下一步将重点围绕流量数据时空关联特性、交通诱导决策、多路段大数据分析等方面进行研究。

[1] 姚卫红，方仁孝，张旭东.基于混合人工鱼群优化SVR的交通流量预测[J].大连理工大学学报，2015，55(6)：632-637.

[2] 芮兰兰，李钦铭.基于组合模型的短时交通流量预测算法[J].电子与信息学报，2016，38(5)：1227-1233.

[3] 董春娇，邵春福，诸葛承祥，等.基于时空特性的交通自由流短时预测状态空间模型[J].土木工程学报，2013，46(8)：111-118.

[4] Vlahogianni E I, Karlaftis M G, Golias J C. Short-term traffic forecasting: Where we are and where we’re going [J]. Transportation Research Part C; Emerging T echnologies,2014,43:3-19.

[5] 商强，杨兆升，李志林，等.基于相空间重构和RELM的短时交通流量预测[J].华南理工大学学报(自然科学版)，2016，44(4)：109-114.

[6] 覃明贵.城市道路交通数据挖掘研究与应用[D]. 复旦大学，2010.

[7] 王建，邓卫，赵金宝.基于改进型贝叶斯组合模型的短时交通流量预测[J].东南大学学报(自然科学版)，2012，42(1)：162-167.

[8] 董宏辉，孙晓亮，贾利民，等.多模态的交通流量预测模型[J].吉林大学学报(工学版)，2011，41(3)：645-649.

[9] TCHRAKIAN T T, BASU B, and O’MAHONY M. Real-time traffic flow forecasting using spectral analysis [J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 519-526.

[10]杨发权，李赞，郝本建，等.基于粒子群优化与SVR-ADLA算法的MIMO系统识别研究[J].高技术通讯，2015，25(1)：24-30.

[11]杨兆军，杨川贵，陈菲，等.基于PSO算法和SVR模型的加工中心可靠性模型参数估计[J].吉林大学学报(工学版)，2015，45(5)：829-836.

[12]王琳，张赟，彭文辉，等.基于人工蜂群优化的支持向量回归机预测方法[J].系统工程与电子技术，2014，36(2)：326-330.

[13]Cuevas E, Cienfuegos M. Zaldiva D, et al. A swarm optimization algorithm inspired in the behavior of the social spider [J]. Expert System with Applications, 2013,

40(16):6374-6384.

[14]聂庆慧，夏井新，钱振东.城市道路交通流短时预测及可靠性分析[J].西南交通大学学报，2013，48(5)：955-960.

[15]程俊，张雪莹，李瑞贤. 基于元学习的软件缺陷预测推荐方法[J].中国电子科学研究院学报，2015，10(6)：620-927.

[16]丛新宇，虞慧群，范贵生．基于组合模型的交通流量预测方法[J]．华东理工大学学报:自然科学版，2011，37(3): 340 -345．

[17]Wanli Mina，Laura Wynter．Real-time road traffic prediction with spatio-temporal correlations[J]．Transportation Research Part C，2011，19(4):73 -78．

[18]Lucas Barcelos de Oliveira，Eduardo Camponogara． Multi-agent model predictive control of signaling split in urban traffic networks[J]． Transportation Research Part C，2010，18(1):120-139．

[19]Dominik Sierociuka，Inés Tejadob，Blas M．Vinagreb． Improved fractional Kalmanfilter and its application to estimation over lossy networks[J]. Signal Processing，2011，91(3): 542-552．

Short-term Traffic Flow Prediction Algorithm Based on FCM and Optimized SVR with Social Spider Optimization Algorithm

CAO Cheng-tao1，LIN Xiao-hui1，XU Lun-hui2

(1.Intelligent Traffic Engineering Technology Center, Guangdong Communication Polytechnic, Guangzhou 510650,China； 2.South China University of Technology, Guangzhou 510640,China)

The short-term traffic flow forecasting problem of intelligent transportation system (ITS) is studied, and a traffic flow prediction algorithm based on combined FCM and optimized SVR with social spider optimization algorithm is proposed. Firstly, the FCM clustering method is used to process the traffic flow data, and the time sequence data modules based on time node segmentation are obtained, which effectively reduce the error caused by the difference of the data. Then, the SVR prediction model based on social spider optimization (SSO) algorithm is constructed. For the disadvantage of parameter selection of SVR, the social hierarchy is introduced to SSO, and the spider population is divided into three different classes dynamically. According to the individual fitness in different classes, the adaptive competition, "fast search" and reverse learning mechanism are designed, helping to improve the accuracy of SSO. Finally, the optimized SVR with SSO is used to predict the short-term traffic flow for each time sequence data module. Simulation results show that, Compared with other prediction algorithms, the average absolute deviation of the algorithm is reduced by 38.4% to 53.8%.

traffic flow forecasting; fuzzy C-means clustering; support vector regression (SVR); social spider optimization

10.3969/j.issn.1673-5692.2017.01.010

2016-10-10

2017-01-20

国家星火计划项目：基于物联网的光伏大棚智能控制技术应用与示范(2015GA780024)；广东省高等学校优秀青年教师培养计划项目：城市交通信号控制实时评价模型及其优化方法研究(Yq2013180)；广东省高等职业教育品牌专业建设项目：智能交通技术运用(2016gzpp044)。

曹成涛(1981—)，男，山东人，副教授，博士，华南理工大学访问学者，主要研究方向：智能交通系统、智能控制技术；

E-mail：jncct@163.com

林晓辉(1981—)，男，广东人，副教授，硕士，主要研究方向为智能交通系统等；

许伦辉(1965—)，男，江西人，教授，博士，主要研究方向为智能交通系统、智能控制。

TP391

A

1673-5692(2017)01-052-08