均质土层中钻孔注水渗透系数求解方法

钱财富

（1.安徽省·水利部淮委水利科学研究院 蚌埠 233000 2.安徽省建筑工程质量监督检测站 蚌埠 233000）

均质土层中钻孔注水渗透系数求解方法

钱财富1，2

（1.安徽省·水利部淮委水利科学研究院 蚌埠 233000 2.安徽省建筑工程质量监督检测站 蚌埠 233000）

本文以基于达西定律为基础，对地下水位以上土层进行钻孔注水试验，利用流量相等的原则试算流线边界，从而给出地下水位以上均质土层的渗透系数估算值。

钻孔注水 一汇流线流 均质土层 渗透系数

1 前言

目前规范中关于现场注水试验渗透系数计算方法大多为地下水位以下情况，对于地下水位较低注水试验段为地下水位以上的渗透系数计算仅《水文地质手册》提供有专门介绍，但计算公式有其局限性，当孔内水头高度较低时计算结果失真较大。本文通过达西定律推求钻孔注水试验的渗透系数计算简化公式，并通过工程实例验证该公式计算结果的合理性。

2 理论分析

假设钻孔注水试验试验段土层均匀，且充分饱和，水平和垂直渗透系数大小相等，且渗透系数大小不随深度变化。水在土体孔隙中渗透时，由于渗透阻力的作用，沿程伴随着能量的损失的渗透规律符合达西定律。

式中：q为渗流量，cm3/s；k为渗透系数，cm/s；i为水力坡降，；A为截面面积。

该钻孔注水试验，按常水头无套管方法进行。根据达西定律，地下水位以上饱和均质土层渗流按一汇线流简化，如图1所示。

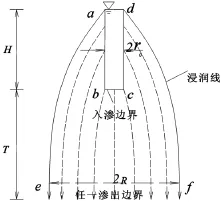
图1 渗流过程示意图

表1 渗透系数估算计算表

由图1可知，其入渗边界为abcd，入渗流量为：

式中：Δh0、Δl0为入渗边界处水头损失和入渗渗径；i0为入渗边界任一点的水力坡降；δ0为入渗边界渗透系数为i0的任一小区域的面积。

选取任一水平渗出边界ef，如图1，其渗出流量为：

由于水头在渗流过程中的沿程损失存在，当边界ef面足够远时，i沿径向不再发生变化，且等于1。那么（3）式为：

q=kA （4）

式中：A为ef面出渗面积，A=πR2。

由于试验段土层充分饱和，所以从入渗面abcd渗入水量和出渗面ef渗出水量应该相等。那么由（1）和（4）式得：

由（5）式得：

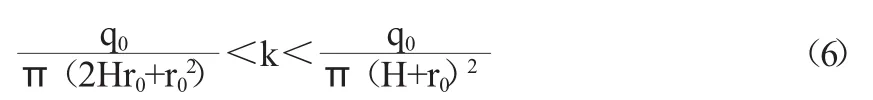
为了更加精确地估算可给定的不同渗透系数求出其渗流场，并对R值进行迭代计算，直至两渗透系数差值较小。

3 应用举例

某工程钻孔深度11.0m，钻孔半径为0.055m，试验时试验段土体充分饱和，注水量为0.0038m3/h。将数值带入（6）式解得：k∈（2.75×10-7，2.77×10-5），cm/s。

根据渗透系数范围值进行选取试算，试算结果如表1所示。

由表1可知，该工程试验段土体渗透系数约为4.29×10-6cm/s。该孔所取芯样，室内渗透系数平均值为7.02× 10-7cm/s。

由于室内试验的局限性，其室内渗透系数一般比现场渗透试验值小。此次计算渗透系数估算值较为合理，基本可以反映该区域土层渗透情况。

4 结论

（1）本文估算结果精度较高，能够满足工程使用要求。

（2）本文公式仅适用均质土层，对于非均匀土层很难求出估计渗透系数下渗出半径R估，若能在现场注水试验时测出其流线形式，亦能通过该文公式进行计算。其结果为试验段土层的平均渗透系数■

（专栏编辑：顾 梅）