汾河流域工业需水预测分析

张国强

（山西省水利水电勘测设计研究院，山西 太原 030024）

汾河流域工业需水预测分析

张国强

（山西省水利水电勘测设计研究院，山西 太原 030024）

汾河流域为全省政治、经济、文化带，水资源短缺是汾河流域存在的主要问题，合理分配水资源和节约用水变得尤为重要。第二产业是国民经济中的支柱产业，合理预测工业需水是河道外需水预测中的重中之重。采用定额法、趋势法和弹性系数法三种方法对工业需水进行了预测和合理性分析。

需水分析；定额法；趋势法；弹性系数法；汾河流域

汾河是山西的第一大河，黄河第二大支流，流域面积39 471 km2，占全省国土总面积的1/4，流域范围涉及全省9市51县，干流全长716 km，自北向南纵贯6市27县。流域内自然资源丰富，生产条件得天独厚，由于经济社会的快速发展和人口的急剧增长，流域内用水量持续增加，加之煤炭开采、植被退化对水资源的影响，生态环境受到了严重破坏。为此，山西省委、省政府高度重视，决定启动实施汾河流域生态修复重大战略工程。

1 概况

汾河发源于宁武县东寨镇管涔山脉楼子山下水母洞，和周围的龙眼泉、象顶石支流汇流成河，干流自北向南纵贯太原、临汾两大盆地，至运城新绛县境急转西行，于万荣县荣河镇庙前村附近汇入黄河，沿途汇聚吕梁、太岳山区50 km2以上的一级支流83条。流域涉及9市51个县（市、区），其中阳泉市、长治市、晋城市6县仅有587 km2，占总面积的1.5%，主要为太原市、晋中市等6市45县（市、区）。2012年汾河流域总人口1 390万人（占全省的38.5%），城镇人口792万人，城镇化率57%；地区生产总值5 213亿元。流域总耕地面积117万hm2，有效灌溉面积47.8万hm2，粮食作物播种面积102.3万hm2，粮食产量502万t。

根据山西省第一次水资源评价结果，1956—1979年系列汾河流域年均降水量为529.0 mm，多年平均水资源总量为36.1亿m3，流域内人均水资源占有量为295 m3。第二次水资源评价结果显示，1956—2000年系列汾河流域年均降水量为505 mm，多年平均水资源总量为33.6亿m3，流域内人均水资源占有量为264 m3。本次规划，1956—2013年系列多年平均降水量为507 mm，多年平均水资源总量为31.9亿m3，流域内人均水资源占有量为229 m3。

由此可以看出，汾河流域水资源量逐渐减少，水资源短缺将是汾河流域存在的主要问题，合理分配水资源和节约用水将变得尤为重要。由GDP占比可以看出，第二产业是国民经济中的支柱产业。因此，合理预测工业需水是河道外需水预测中的重中之重。

2 工业增加值预测

规划在2020年以前，汾河流域工业增加值平均增长速度为7.0%，工业增加值4 136亿元；2021—2030年期间，工业增加值年平均增长速度为5.3%，工业增加值6 938亿元。

3 工业需水预测

工业需水预测方法有定额分析法、趋势法、重复利用率提高法、弹性系数法等。本次规划采用定额法、趋势法和弹性系数法对工业需水预测。

3.1 定额法

定额法是根据经济社会发展水平、水资源市场变化趋势，预测将来各行业用水定额指标，进而估算需水量的方法。定额法概念明确、容易掌握，实际工程中使用较多，计算公式为：

式中：Q——预测年需水量，亿m3；

qi——国民经济各部门用水定额；

pi——各预测年国民经济各部门经济指标。

仅计算工业需水，故为万元工业增加值用水量，即规划水平年工业增加值。

2012年汾河流域内工业用水量为5.2亿m3，万元工业增加值用水量为22.3 m3，管网漏失率18%。本次规划分别计算每个县市现状年万元工业增加值用水量，并根据现状年万元工业增加值用水量来预测规划水平年的万元工业增加值用水量。当万元工业增加值用水量较小时，说明该县市的节水潜力很小，该县市规划水平年的万元工业增加值用水量就小幅减少或维持现状；当万元工业增加值用水量较大时，说明该县市的节水潜力较大，该县市在规划水平年的万元工业增加值用水量就应大幅减少。

在上述原则指导下，经过计算工业需水2020年为10.27亿m3，2030年为11.93亿m3。2030年万元工业增加值用水量为17.2 m3。

3.2 趋势法

趋势法是用历年工业用水增长率推算未来工业用水量。预测不同水平年的需水量计算式为：

式中：Si——预测的某水平年工业需水量，亿m3；

S0——基准年（起始年份）工业用水量，亿m3；

d——工业用水年平均增长率，%；

n——从起始年份至预测水平年所间隔的年数。

2001—2012年山西省工业用水量及工业增加值见表1。

表1 山西省工业用水量及增加值统计表

系列选用表1中2001—2012年数据，预测工业需水为2030年6.9亿m3，万元工业增加值用水量为9.95 m3；系列选用2008—2012年数据，预测工业需水为2030年9.8亿m3，万元工业增加值用水量为14.1 m3。3.3 弹性系数法

弹性系数法是根据某个部门需水量增长率与其特征指标增长率之间的比值（此比值称为弹性系数）预测未来的需水量。需水量弹性系数的定义为：

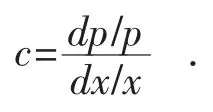
式中：c——弹性系数；

p——需水量，亿m3；

x——部门特征指标，本次为工业增加值。

弹性系数一般根据统计资料和专家的判断来确定。系列选用表1中2008—2012年数据，经计算弹性系数为0.27，本次选取0.3作为弹性系数进行工业需水预测，结果为2020年工业需水6.52亿m3，2030年工业需水7.84亿m3。2030年定额为11.3 m3/万元。

3.4 合理性分析

本次规划分别采用定额法、趋势法和弹性系数法对工业需水进行了预测。预测出2030年工业需水量分别为11.93亿m3，6.9亿m3，7.84亿m3。

选用2008—2012年系列，万元工业增加值用水量年均减少7.3%，考虑到汾河流域2012年万元工业增加值用水量22.3 m3，已经较低，未来节水潜力较小。故本次预测万元工业增加值用水量年均减少4%，经计算汾河流域2030年万元工业增加值用水量为10.7 m3，与弹性系数法计算成果接近。故认为弹性系数法计算成果是合理的。

4 结语

工业用水是城镇用水的重要组成部分，在整个城镇用水中，工业用水不仅所占比重大，而且增长速度快，用水集中，城市水资源紧张主要是工业用水问题造成的。因此，合理预测工业需水对合理配置水资源具有十分重要的作用。

TU991.31

C

1004-7042（2017）01-0020-02

张国强（1983-），男，2007年毕业于河海大学水文与水资源工程专业，工程师。

2016-11-03；

2016-12-15