基于多路径的城市轨道交通网络末班车动态可达性研究
张 亮 吕利民 叶红霞 徐瑞华
(1.同济大学交通运输工程学院,201804,上海; 2.广州地铁集团有限公司运营事业总部线网管控中心,511430,广州∥第一作者,硕士研究生)
基于多路径的城市轨道交通网络末班车动态可达性研究
张 亮1吕利民2叶红霞2徐瑞华1
(1.同济大学交通运输工程学院,201804,上海; 2.广州地铁集团有限公司运营事业总部线网管控中心,511430,广州∥第一作者,硕士研究生)
城市轨道交通网络末班车动态可达性基于空间可达性的时间可达性。空间可达性为路网的有效路径集,取决于路网物理结构、有效路径K值、换乘走行时间和区间运行时间等。时间可达性是在空间可达性有效路径集的基础上,匹配列车时刻表和换乘走行时间,从而确定各路径的末班车时间以及OD(起讫)对的末班车时间。分别从空间可达性和时间可达性两个方面着手,研究网络末班车动态可达性推算方法,并以广州轨道交通路网为例,验证了该方法的有效性和可行性。城市轨道交通网络末班车动态可达性计算可为乘客提供末班车时刻查询以及相应的可达路径信息。
城市轨道交通; 末班车; 动态可达; 多路径
First-author′s address School of Transportation Engineering,Tongji University,201804,Shanghai,China
近年来,我国城市轨道交通迅猛发展,北京、上海、广州等城市的轨道交通已相继进入网络化运营时代。在城市轨道交通路网中,由于各线的运营时间不同,末班车结束运营的时间也不同,导致路网中各站点之间的可达性随着时间而变化。在末班车时段,随着时间的推移,网络所有起讫点(OD)间从全部可达转变为全部不可达,当乘客对城市轨道交通运营时间了解不准确时,容易造成在起始站点购票成功,但经过一次或多次换乘后,需换乘的线路己停止运营,无法抵达目的车站的情况。国外学者对基于时刻表的城市轨道交通网络路径搜索求解算法进行了研究[1-4],但缺乏对末班车可达性的研究。国内学者在路径搜索求解算法[5]和末班车动态可达路径方面均有研究[6-8]。本文在国内外研究成果的基础上,对城市轨道交通网络路径和基于列车时刻表的末班车动态可达性进行研究,为末班车时段乘客出行提供信息支持,保障乘客在购票时获得足够的信息来确认能否成功搭上末班车,以及相应的乘车路径。
城市轨道交通网络末班车动态可达性包括空间可达性和时间可达性。在城市轨道交通路网中,任意两个车站之间只要连通,就有空间可达性。时间可达性是指由于各条线路运营时间不一致,网络中两个车站不同路径之间的可达性随着时间的推移而变化,即动态可达性。也就是说,末班车动态可达性是基于物理路网空间可达性的时间可达性。空间可达性主要受到路网物理结构和OD两点在路网中所处位置的影响。时间可达性基于列车运行图和换乘走行时间,与OD之间的各条有效路径的可达性相关。本文从空间可达性和时间可达性两方面对末班车动态可达性进行研究,在空间可达性的基础上确定多条有效路径,对各路径的时间可达性进行求解计算,确定路网中各车站的末班车动态可达性,并对广州现有的城市轨道交通网络进行实例分析。
1 空间可达性
理论上,城市轨道交通路网上任意两点之间均是可达的,且可达路径不唯一。然而,不同路径的换乘次数和走行距离不同,导致许多换乘次数多、走行距离长的绕行路径不被乘客选择,为无效路径。在途时间越少,换乘次数越少,走行距离越短,路径越便捷,乘客选择的可能性越大。而末班车乘客对可达性的要求比对其他便捷性条件的要求高,甚至为了可达,可以选择一定程度的绕行路径。因此,在确定物理路网路径时,以时间为阻抗,考虑路网中区间运行时间和换乘走行时间,采用K短路径来确定城市轨道交通末班车动态可达性的空间可达性。
1.1K值确定方法
K短路径搜索算法中的K值需依据乘客的特性、末班车乘客的意愿,进行问卷调查确定。为确定K短路径搜索中的K值,引入路径伸展系数Hst。OD对(s,t)之间的有效路径k满足:k的阻抗在最短路径阻抗的(1+Hst)倍之内。即
式中:
Ck,st——OD对(s,t)第k条路径的阻抗。
Hst值可以根据乘客意愿,通过问卷调查确定。在进行问卷设计时,以时间为阻抗,以最短路为基准,在最短路不可达的情况下,让乘客在比最短路长度多Hst倍的可达路径和放弃乘坐城市轨道交通作出选择。其中Hst可以取不同的值。根据问卷调查结果来确定K值。在路径搜索时,当搜索到的路径为第K短路径时停止该OD对的路径搜索。
1.2 换乘走行时间
换乘站走行时间ti,hc是指换乘乘客从输送线路列车下车步行到衔接线路站台所需要的时间。换乘走行时间是路径阻抗的一部分,也是确定末班车动态可达性匹配的关键因素。
对于城市轨道交通乘客而言,换乘需要经历走行、候车等待等过程,走行舒适度低,等待时间无法掌控,容易产生焦躁心理。在整个出行过程中,换乘走行时间比乘客乘车时间的阻抗更大,花同样多的时间,乘客更愿意乘车而不是换乘走行。因此,在确定K短有效路径时,需要考虑乘客对走行时间的接受程度,对换乘走行时间进行转化:
式中:
Ti,hc——转化后用于路径阻抗计算的换乘走行时间;
ti,hc——乘客在换乘站i的走行时间;
Ci,hc——转化系数,可通过对乘客意愿的调研来确定。
不同的乘客群,走行速度不一样,导致其走行时间不一致;车头与车尾的乘客,走楼梯和乘电梯的乘客,其换乘走行时间也不同。换乘走行时间的确定直接影响着乘客能否换乘成功,取值太大,会误导原本能成功换乘的乘客,导致其放弃乘坐轨道交通,造成损失;取值太小,则会使得走行速度较慢的乘客在入闸后无法成功换乘,增加乘客的投诉。因此,在确定末班车动态可达模型中的换乘走行时间时,需对不同换乘站间不同换乘方向的换乘走行时间进行调研,保障换乘走行时间的取值能满足大部分末班车乘客顺利换乘。
因此,在计算末班车动态可达性时,有必要对乘客在各换乘站的走行时间ti,hc进行调研,在路径搜索算法中对换乘走行时间进行转化,在动态可达模型算法中选取合适的换乘走行时间进行计算。
1.3 有效路径集
城市轨道交通末班车动态可达性是基于物理路网空间可达性的时间可达性。空间可达性通过K短有效路径集表示,以乘车时间为阻抗,将换乘节点的换乘走行时间换算为乘车时间阻抗。为确定路网有效路径集P,先对路网结构进行简化,以车站为点,区间为边,区间运行时分为边的权重,形成路网拓扑结构图。需要注意的是,该网络拓扑图上的点具有线路属性,不同线路间的换乘站分别为不同的点,同一换乘站间的边的权重为Ti,hc。
采用K短路径算法,计算全网路径集P={Pij,i∈N,j∈N},其中,N为路网拓扑结构中点集,OD对(s,t)之间的路径集Pst={Pi,st,1≤i≤k}。然而,并非任一OD间的有效路径集Pst都有K条有效路径,在K值确定的情况下,路网中存在部分OD对,尤其是无需换乘的OD对,其次短路径阻抗比最短路径大很多,或者其第i+1条路径比第i条路径阻抗大很得多,同样为乘客不愿选择的无效路径。因此,pi,st短路径除了满足第K短路径外,还需满足阻抗处在最短路径阻抗的相对域值(1+Hst)minCk,st倍之内,以及pi,st短路径阻抗与最短路径阻抗相差的绝对值在一定的域值Qst内。Hst、Qst均需通过乘客意愿确定。在计算得到的全网K短路径集中,须分别对各路径pi,st进行相对域值和绝对域值的判断,剔除相应的无效路径,得到全网有效路径集。
2 网络末班车动态可达性计算
由于网络中各线路列车运行计划不同,网络OD之间的可达性随着时间不断变化,同一OD之间的不同路径的可达性也随着时间而变化。对于特定OD对、特定路径,其可达性的关键在于判断路径的O站是否可达及换乘站是否可达。随运营时间的网络动态可达性,是基于列车运行图,结合乘客乘车时刻、OD路径,并通过路径与运行图的匹配,计算乘客进站上车、随车位移、换乘走行等时间,预估乘客从某一时刻进站的所有有效路径的可达性情况。
2.1 计算思路
城市轨道交通末班车乘客在网络中的出行过程分为两大类,一是OD间无需换乘的乘客,二是OD间需要换乘的乘客。对于OD间无需换乘的乘客,能在O站开往目的站方向的末班车之前乘车,便可以顺利到达D站。即在起点站开往目的站方向的末班车之前,OD对在该路径上具有可达。这种情形下,末班车的选择具有唯一性。对于OD间需要换乘的乘客,路径可达需满足两个条件:一是进站乘车时间应在该站开往换乘站方向的末班车之前;二是满足路径上全部换乘站换乘方向的末班车时间要求。这种情形下,需根据途经换乘站的末班车时间的衔接情况进行推算。其主要依据为各条线路的运营基础资料及各线路列车时刻表。
换乘乘客完成一次出行的步骤为:O站购票,进闸机,走行至站台,候车,乘车,下车走行至换乘站台,候车,乘车,D站下车走行出站。考虑到不同车站、不同时间购票排队情况不同,有些持交通卡乘客无需购票;不同车站从进站闸机到站台距离不尽相同,甚至同一车站不同闸机到站台距离有较大的差异;应用到不同系统终端时所需增加的参数不同,本文所研究的末班车出行时间为O站站台的上车时间至D站下车时间,不包括乘客购票时间、从闸机进站后至站台的走行时间和D站出站走行时间等。但将其应用到不同系统终端时,需进行相应的处理。为保障本文的末班车出行时间应用到不同末班车乘客出行查询系统时的准确性,需针对不同车站进行调研,设定本站购票时间、入闸时间以及走行至站台时间等参数。应用到官网信息查询或手机APP查询终端时,各路径出行时间需加上购票时间、入闸时间和进站走行时间;应用到TVM(自动售票机)终端时,各路径出行时间需加上入闸时间和进站走行时间。
在末班车动态可达性计算过程中,以设定时刻或OD路径查询时刻为基准,乘车时刻与车次可从时刻表上获得,结合列车时刻表依次考虑各个环节时间耗费,推算该路径的换乘站是否有接续列车。倘若在推算某条路径的可达时,计算到某个时间节点,在对应的列车运行图上没有能够到达目的车站的列车,则这条路径即为不可达,相应地,OD之间可达路径集合中要剔除这条路径。若OD对间有效路径集Pst中所有路径均为不可达路径,则该OD对不可达;否则,该OD对可达。
2.2 算法步骤
城市轨道交通网络末班车动态可达性以有效路径为基础,以列车时刻表所涵盖的区间运行时间、停站时间、各站末班车时间等内容为依据,综合考虑乘客在换乘站的换乘时间ti,hc进行推算。推算步骤如下:
步骤1:建立城市轨道交通网络的拓扑结构,导入列车时刻表信息。
步骤2:进行OD间路径搜索,根据轨道交通物理网络、区间运行时间和换算后换乘走行时间搜索OD间的K短路径集,再根据相对域值和绝对域值确定路网各OD对间有效路径集P。
步骤3:OD间路径可达性确定,对于给定的一条路径,基于列车时刻表信息,根据路径起点站到路径上其他各站所需时间(包括由起点站到其他站间的区间运行时间、停站时间和换乘时间),推算起点站乘车的一个最晚的有效时间,使之能满足路径上各站(主要是换乘站)的末班车时间要求。起点站的最晚有效时间定义为该路径的末班车时间。推算方法如下:
(1) 设计算路径为O→X1→b→X2→a→X3→D,其中,a、b表示换乘站,X表示相应的车站集,采用倒推的方式。
(2) 取出第一个换乘站a,记下换乘站a向D站方向的末班车发车时间ta,tA=ta为该路径中换乘站a的末班车时间。
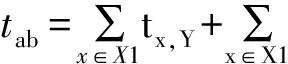
(4) 同样的,可确定O站的末班车时间tO=min{to,tB-tob}。若相应的换乘站更多或者更少,按相同的方法确定各换乘站的末班车时间。
(5) tO为该路径的末班车时间,tb、ta等为各换乘站的末班车时间;
(6) 比较查询时间(或设定时间)与tO的大小,若查询时间(或设定时间)比tO大,则该路径不可达;否则,该路径可达。
步骤4:OD可达性确定,根据OD间有效路径集Pst={pi,st,1≤i≤k},依次计算各路径的末班车时间ti,O,则该OD的末班车时间集TO={ti,O,1≤i≤k},取max{ti,O}为该OD的末班车时间,比较查询时间(或设定时间)与该OD的末班车时间,若查询时间(或设定时间)比该OD的末班车时间大,则该OD不可达;否则,该OD可达。
步骤5:全网可达性确定,依次遍历全网各OD、各路径,确定全网络的末班车时间Tx,O,x∈N。
步骤6:网络末班车时刻输出和特定OD对可达性查询。
网络末班车推算流程图和特定OD对动态可达性流程图如图1所示。
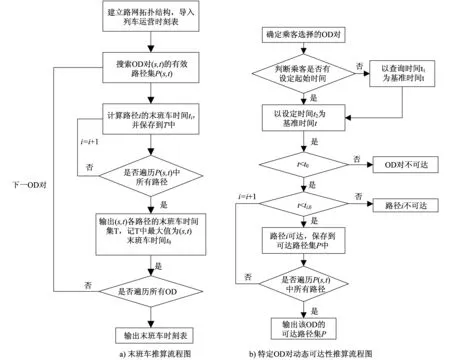
图1 末班车和动态可达性推算流程图
3 算例
以广州轨道交通现有路网为例,基于路网运营时刻表,对网络末班车动态可达性进行分析。广州现有城市轨道交通线路9条(不包括珠江新城APM(旅客自动输送)系统,3号线、3号线北延段为不同线路),运营车站160座(换乘站重复计算),已形成网络化运营。根据路网线路情况,建立城市轨道交通网络拓扑结构,并导入列车运营时刻表信息。广州地铁公司的路网有效路径计算所取K值为3,考虑到本文的研究对象为末班车时段路径,在此条件下乘客更注重可达性而非舒适性和便捷性,算例中K值取5。换乘走行时间是计算可达性的一个关键指标,其取值的合理性一定程度反映了网络末班车可达性的准确性,需要针对不同车站、不同乘客群做相应的调研后确定,本算例中为方便计算,采用站务员换乘走行时间进行计算。
根据基础路网信息以及时刻表信息,对网络路径和网络末班车动态可达性进行计算,得到全路网的末班车时间和OD对间各路径的末班车时间和路径。
输出全路网所有车站的末班车时间并进行统计分析,如表1所示。截至21:00:00前,全网所有车站均可达,自21:01:24开始出现不可达。随着时间的推移,全网车站可达率逐渐降低,22:15:00—22:45:00内可达率下降幅度较快,至次日凌晨0:19:50全部车站均不可达。
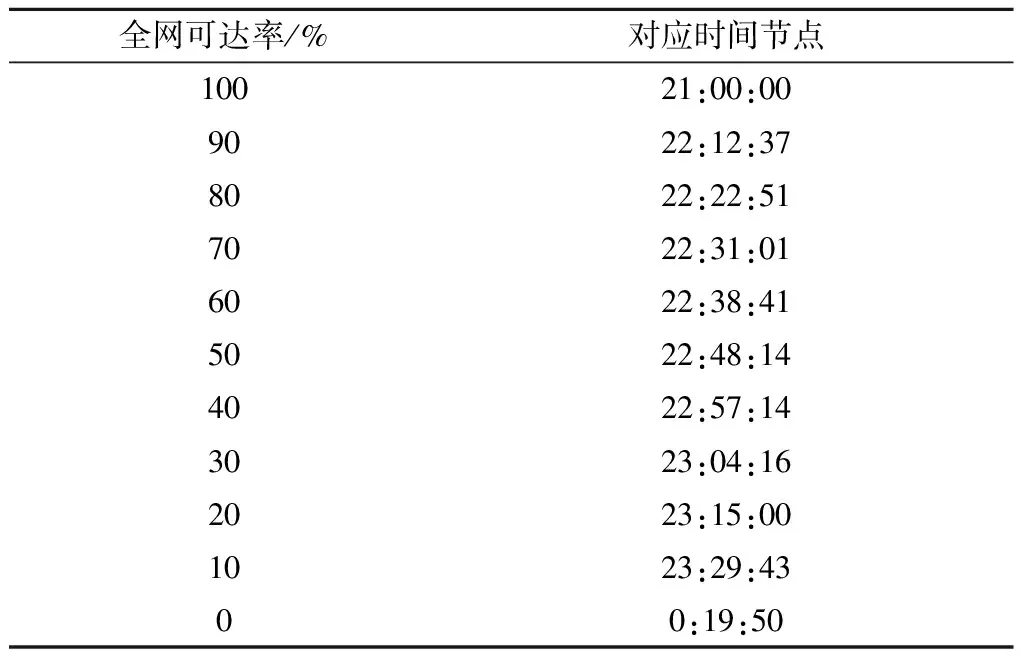
表1 广州网络末班车时间分布
针对乘客查询的特定OD对,计算出相应的路径和末班车时间,以体育西路站到坦尾站和客村站到纪念堂站两个OD对为例,其路径和路径末班车情况如表2所示。
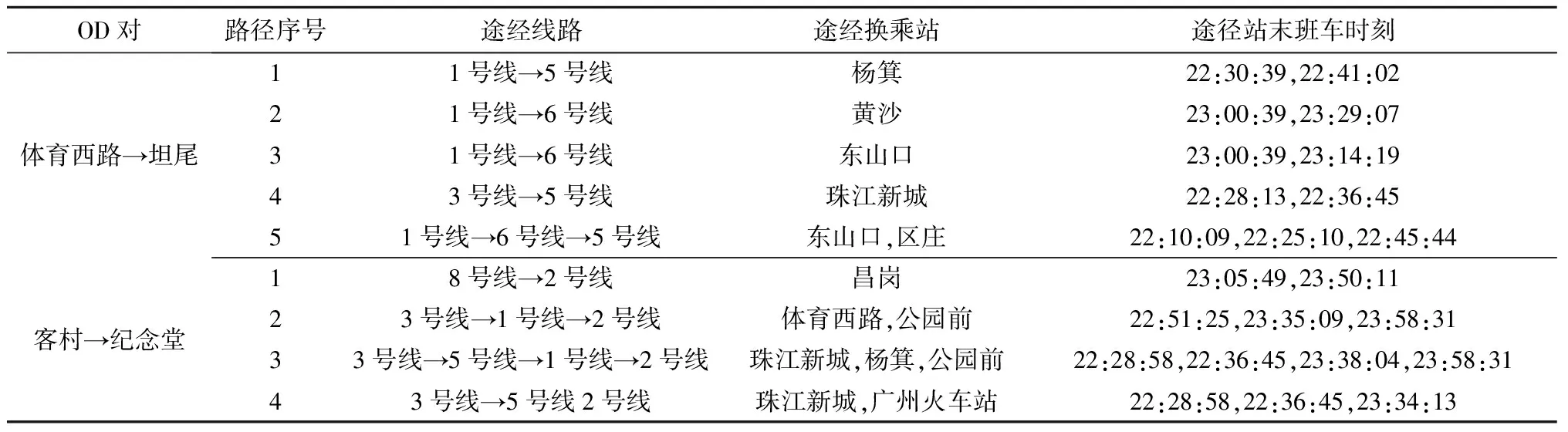
表2 特定OD对路径末班车情况
当乘客查询特定OD对的末班车可达性时,OD对可达则提供相应的可达路径,OD对不可达则告知乘客不可达。在22:30:00、23:00:00、23:30:00时上述两个OD对的可达性情况和可达路径如表3所示。

表3 特定OD对可达路径信息
4 结语
城市轨道交通进入网络化运营阶段,由于“一票换乘”及各线路运营结束时间不同,乘客在缺乏末班车运营时间和路径时间等信息支持的情况下,容易导致购票成功但无法抵达目的地的情况。本文从空间可达性和时间可达性两方面对城市轨道交通网络末班车动态可达性进行研究,空间可达性取决于路网物理结构、有效路径K值、换乘走行时间和区间运行时间等;时间可达性是在空间可达性有效路径集的基础上,匹配列车时刻表和换乘走行时间,从而确定各路径的末班车时间以及OD对的末班车时间。最后以广州轨道交通路网为例,验证动态可达性计算方法的有效性和可行性。城市轨道交通网络末班车动态可达性计算能为乘客提供相应的末班车时刻以及可达路径信息查询。
[1] WONG S C,TONG C O.Estimation of time-dependent origin-destination matrices for transit networks[J].Transportation Research Part B:Methodological,1998,32(1):35-48.
[2] HUANG R,PENG Z.Schedule-based path finding algorithms for transit trip planning systems[J].Journal of Transportation Research Board:Transportation Research Record ,2002,1783(1):142-8.
[3] JIN Y,Yen.Finding the K shortest Loopless Paths in a Network[J].Management Science,1971,17(11):712-716.
[4] SUNG K,BELL M,SEONG M,et al.Shortest paths in a network with time-dependent flow speeds[J].European Journal of Operational Research,2000,121(1):32-39.
[5] 张新.城市轨道交通末班车的动态最优可达路径研究[D].北京:北京交通大学,2014.
[6] 罗钦,徐瑞华,江志彬,等.基于运行图的轨道交通网络动态可达性研究[J].同济大学学报(自然科学版),2010(1):72-75.
[7] 郭建媛,贾利民,秦勇.运行计划约束下的动态可达性分析与计算[J].交通运输系统工程与信息,2015(1):118-122.
[8] 徐杰,张新,郭建媛,等.基于末班车时刻表的城市轨道交通客流诱导系统的研究[J].中国铁道科学,2014(2):111-119.
Dynamic Accessibility of the Last Train in Urban Mass Transit Network Based on Multipath
ZHANG Liang, LYU Limin, YE Hongxia, XU Ruihua
The dynamic accessibility of the last train in urban mass transit network is based on the time accessibility of space accessibility. Space accessibility means the set of valid path, depending on the physical structure of network, value K, walking time in transfer and interval running time. After obtaining the set of valid path, time accessibility is used to calculate the time of last train based on timetable and walking time in transfer. By focusing on both space accessibility and time accessibility, a model of dynamic accessibility of the last train in urban mass transit network is established. To verify the validity and feasibility of the model, Guangzhou urban mass transit network is taken as an example to calculate the last train time schedule and provide passengers with reliable information.
urban mass transit; the last train; dynamic accessibility; multipath
U 292.4
10.16037/j.1007-869x.2017.01.011
2016-03-21)

