基于悬链线理论的跨接软管安装计算

边大勇，闫斌，郑炳祥

基于悬链线理论的跨接软管安装计算

边大勇，闫斌，郑炳祥

考虑到海洋石油平台之间和浮式生产储油装置(FPSO)与单点系泊系统之间的跨接软管成本昂贵，并且在安装过程中极易受损，为保证软管在安装过程中的完整性，提升安装作业效率，降低安装成本，采用悬链线理论对跨接软管安装过程进行分析，建立求解跨接软管长度、连接点角度、受力、高差以及弯曲半径、重心位置等关键控制参数的悬链线方程。在LF13-2油田开发项目跨接软管的安装过程中的应用表明，该方法快捷有效，可作为跨接软管安装控制的理论依据。

跨接软管；悬链线理论；安装计算；海洋石油平台

海洋油气输送软管由于具有良好的抗腐蚀、耐酸碱能力、高压承压能力以及良好的柔韧性已广泛应用于海洋石油平台之间和浮式生产储油装置(FPSO)与单点系泊系统之间原油、天然气和生产水跨接输送的关键设施。该类型海洋油气输送软管由内胶层、内保护层、钢丝编织层、中间胶层、外保护层和外胶层符合而成，见图1。

该类型软管价格昂贵，多为国外进口，并且在安装过程中对软管弯曲形状、软管受力，以及软管对接点位置和角度都有严格要求，不合适的海上安装方法将造成软管结构损伤，导致使用寿命的降低，危及海洋油气输送的安全和海洋环境。为此，针对海洋石油平台之间和浮式生产储油装置(FPSO)与单点系泊系统之间的跨接软管，结合安装过程中的关键控制点，利用悬链线方程近似方法进行分析计算，以期为海上跨接软管安装工程提供依据。

1 问题的提出

海洋石油平台之间和浮式生产储油装置(FPSO)与单点系泊系统之间跨接软管的安装过程中，主要面临以下问题。

1)跨接软管2端连接点一般不等高，获得跨接软管最低点与2端连接点的高度差之后才能确定吊装索具的配置。

2)跨接软管2端连接点采用法兰连接，必须获得连接点受力大小以及受力角度，才能预制跨接软管连接弯头角度，以及确定跨接软管吊装或拖拉设备的型号。

3)跨接软管采用U形吊装或拖拉，在安装过程中，必须控制跨接软管的弯曲程度大于其弯曲半径，以免损伤软管。

在以往的工程实践中，作业者多依靠经验进行跨接软管的安装，尤其是跨接软管2端连接点角度、软管2端高差、吊装和拖拉过程中软管弯曲半径须多次进行摸索和尝试，才能最终确定软管安装和连接状态，导致安装过程时间长且软管易遭受损坏， 因此对跨接软管安装过程受力状况的分析和计算成为提高海上施工的作业效率和保障跨接软管安装过程完整的关键环节。

2 计算的可行性分析

根据悬链线理论，当跨距足够大时，所有的悬挂缆索都可看成柔软而无刚性的悬链。基于此，国内许多学者采用悬链线理论对深水立管[1-2]、锚泊系统[3]、架空索道单跨钢索[4-5]、轨道车辆间跨接电缆[6]、高压架空输电线路[7]、大跨径悬索桥[8]等进行了有益的探索和实践。海洋石油平台之间和浮式生产储油装置(FPSO)与单点系泊系统之间的跨接软管与架空索道单跨钢索类似，软管长度长，跨度大，见表1，其悬垂的物理状态近似于悬索状态。

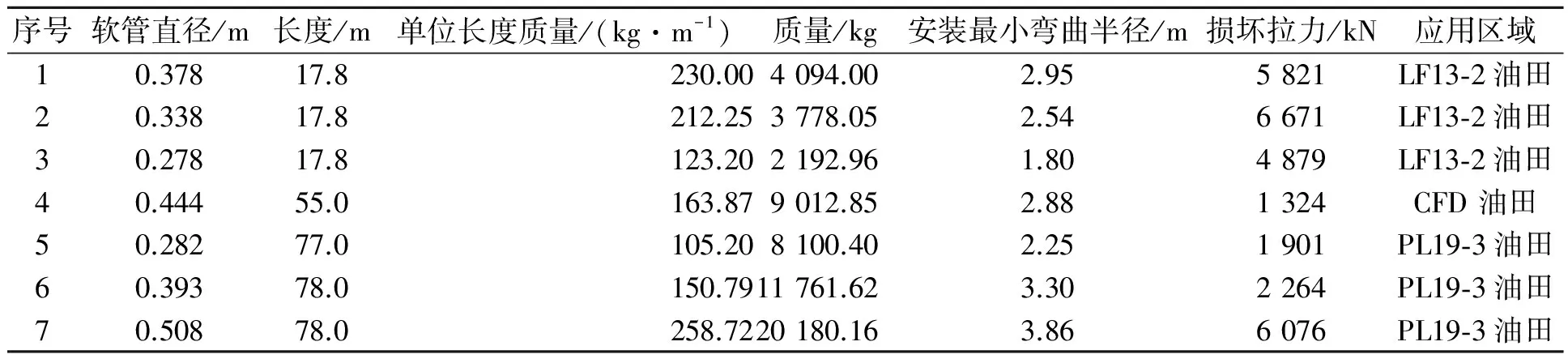
表1 跨接软管设计参数

虽然跨接软管两端带有连接法兰并经过特殊加强处理，但加强处理段及法兰占软管总长和总质量比重较小；虽然跨接软管有一定的刚性，但横截面面积在自重作用下变化十分微小，并且软管截面尺寸、弯曲半径与其长度、跨度相比十分微小。因此，悬挂在海洋石油平台之间和FPSO与单点系泊系统之间的大长度、大跨距的跨接软管可认为符合悬链线形态，并可利用悬索理论进行受力分析。

目前应用较多的悬索理论主要有抛物线理论和悬链线理论，由于悬链线理论关于悬索竖向载荷沿索弧长均匀分布的假设更接近跨接软管的实际形态，且对存在一定挠度的悬索具有相对更高的计算精度[9-10]，因此，采用悬链线理论对跨接软管安装过程进行计算分析更为合适。

为了便于适用于跨接软管安装的悬链线方程的建立，将以下假定作为分析计算的基础。

1)跨接软管是理想柔性的，因为软管的截面尺寸、弯曲半径与软管长度、跨度相比十分微小，故截面的抗弯刚度在计算中可不考虑。

2)跨接软管自重沿管线均匀分布，符合胡克定律。

3)跨接软管的横截面面积在自重作用下变化十分微小，可以忽略。

3 跨接软管安装的理论分析

3.1 跨接软管悬链线方程的建立

跨接软管的跨接方式有等高跨接和不等高跨接2种情况，本文以不等高跨接情况为例进行分析。

如图2所示，跨接软管悬挂在A、B2点之间，成悬链线形，在自重和A、B两点拉力作用下保持平衡、静止状态。取较低连接点A为坐标原点，建立平面直角坐标系，取一微段dS，如图3。设H0为跨接软管的水平拉力(N)；q为跨接软管单位长度重力(N/m)；A、B2点跨距为D；高差为h，弦倾角为α。

由力的平衡条件可得悬链线微分方程为

(1)

由边界条件：x=0，y=0，x=D，y=Dtanα=h可得以跨接软管较低连接点为坐标原点的悬链线方程。

(2)

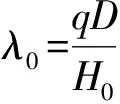
3.2 跨接软管安装相关参数的推导

3.2.1 跨接软管2端连接点的角度

由式(2)可得任意点切线斜率为。

(3)

将xA=0、xB=D代入式(7)，求得跨接软管两端连接点的斜率及角度。

(4)

(5)

3.2.2 跨接软管2端连接点的高差

将xA=0、xB=D分别代入式(2)，可得A、B两点高差h。

(6)

3.2.3 跨接软管的长度

设跨接软管曲线长度为L，则A、B2点曲线长度为

将xA=0、xB=D和式(7)代入上式，可得软管长度方程。

(7)

利用双曲函数的和差公式对式(6)、(7)进行变换，可得软管2端连接点高差与软管长度关系的方程。

(8)

3.2.4 跨接软管任意点拉力的计算

设T为软管上任意点的悬链拉力，则有：

(9)

3.2.5 跨接软管重心的计算

设跨接软管在悬链型态下重心坐标为xw、yw，由于跨接软管质量沿管线及截面均匀分布，可得跨接软管在悬链型态下重心坐标。

将xA=0、xB=D和式(7)带入上式可得：

在跨接软管2端等高的情况下有：

(11)

3.2.6 跨接软管曲率半径

曲率半径ρ为

(12)

将式(2)代入式(12)可得：

(13)

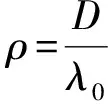
4 跨接软管安装施工案例计算

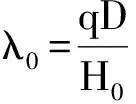
4.1LF13-2油田开发项目案例计算

以LF13-2 油田开发项目中跨接软管的安装为例进行计算。该项目跨接软管安装的设计参数见表2。

计算结果如下。

1)将跨距、高差、软管长度、软管单位质量代入方程(8)，通过迭代法求得无荷水平拉力系数λ0=2.752；

表2 跨接软管安装的设计参数

2)将跨距、高差、无荷水平拉力系数代入跨接软管最低点横坐标，可得xC=5.953 m；

3)将跨距、软管最低点横坐标、无荷水平拉力系数代入方程(4)、(5)，可得跨接软管较低连接点处垂直方向与软管夹角角度θA=-58.0°，θB=64.9°；

4)将跨接软管2端A(0,0)、B(D，h)及软管单位质量、跨距、无荷水平拉力系数、软管最低点横坐标代入式(9)，可得2端连接点所受拉力分别为：TA=18 705.56 N，TB=23 364.87 N；任意点水平受力H0=9 909.71 N；

5)将上述数据代入方程(10)，可得跨接软管连接后重心坐标为：xw=6.99 m，yw=-0.35 m；

6)跨接软管连接后其曲率半径最小位置位于软管最低点即xC=5.953 m处，此时曲率半径为ρ=4.76 m。

4.2 对跨接软管安装施工控制的建议

根据以上计算结果对软管安装过程提出以下建议。

1)在平台侧预制跨接软管连接弯头时，较低连接点弯头角度应为-58.0°，较高连接点弯头角度应为64.9°。

2)在平台侧拖拉软管末端与连接弯头适配时，所需最大拉力为23 364.87 N，取2倍安全系数，拉力大于4.77 kN以上的绞车即可满足需求，可选50 kN的绞车进行现场施工。

3)跨接软管连接状态下中心位置偏向较低连接点，因此配备索具时较低连接点侧索具应短于较高连接点，所配备索具长度可通过重心位置计算获得，保证起重机械勾头处于重心的垂线上。

4)跨接软管安装操作最小曲率半径4.76 m远大于软管设计曲率半径2.54 m，因此，软管安装作业不会对软管自身造成损坏。

5 结束语

1)使用悬链线方程在跨接软管安装施工过程中对软管弯曲形状、软管受力以及软管对接点位置和角度进行分析和计算，且在计算过程中忽略跨接软管直径及刚度等参数，简化计算过程是可行的。

2)对于跨接软管，只要跨距D、单位长度重力q、高差h或弦倾角α和软管长度L或任意一端连接点拉力等4参数确定，跨接软管的几何形状和受力状态就可完全确定。

3)通过计算可求得跨接软管安装施工过程中对软管弯曲形状、软管受力以及软管对接点位置和角度等关键参数指标。在LF13-2油田开发项目中跨接软管安装的实践表明，该计算结果与工程实际结合良好，为方案设计和现场实践提供了可靠的依据和指导。

4)计算过程中忽略跨接软管直径及刚度等参数，使计算结果与实际情况略有偏差，在实际生产实践中，可对安装过程中软管弯曲半径和软管2端连接点角度进行适当修正。

[1] 康庄，康有为，梁文洲.深海钢悬链线立管(SCR)安装强度分析[J].船海工程，2012，41(1):92-95.

[2] 李鹏，李彤，张鸿凯，等.深水FPSO柔性立管[J].中国造船，2010，51(2):378-385.

[3] 王丹，刘家新.一般状态下悬链线方程的应用[J].船海工程，2007，36(3):26-28.

[4] 郑丽凤，周新年.悬链线理论及其应用研究Ⅴ单跨索道多荷重悬链线算法理论推导[J].福建林学院学报，2002，22(1)：13-16.

[5] 郑丽凤，周新年，胡永生，等.悬链线理论及其应用研究Ⅵ单跨索道多荷重悬链线算法数学模型[J].福建林学院学报，2002，22(2)：109-112.

[6] 王长昌.基于悬链线方程的跨接电缆长度计算[J].铁道车辆，2013，51(6)：4-33.

[7] 姜广智.悬链线方程在高压架空输电线路中的应用[J].科学技术与工程，2008(8)：1960-1964.

[8] 黄平明，梅葵花，徐岳.大跨径悬索桥主缆系统施工控制计算[J].西安公路交通大学学报，2000，20(4)：19-28.

[9] 郑丽凤，周新年，巫志龙.悬索的理论计算与实测误差分析[J].北华大学学报：自然科学版，2010(4)：162-168.

[10] 董耀甫，杨旗.索道悬索理论精度分析[J].森林工程，2001(3)：31-32.

(海洋石油工程股份有限公司，天津 300451)

Calculation of the Jumper Hose Installation Based on Catenary Theory

BIAN Da-yong, YAN Bin, ZHENG Bing-xiang

(China Offshore Oil Engineering Co., Ltd., Tianjin 300451, China)

The jumper hose between offshore oil platforms or floating production storage and offloading units (FPSO) and single point mooring system is very expensive and easily damaged during the installation process. In order to ensure the integrity of hose and improve installation efficiency and reduce the installation cost, the catenary theory was used to analyze the installation process, and a series of equations were deduced to solve the key control parameters such as jumper hose length, angle and force on hose end, height difference between hose control points, bending radius and the center of gravity. The method was proved to be very efficient and quick during the jumper hose installation in LF13-2 oilfield development project, so it can provide theoretical basis for jumper hose installation.

jumper hose; catenary theory; installation calculation; offshore oil platforms

10.3963/j.issn.1671-7953.2017.01.031

2016-05-17

海洋石油工程股份有限公司陆丰13-2Ⅱ期油田开发项目

边大勇(1967—)，男，学士，高级工程师研究方向:海洋石油工程

P752

A

1671-7953(2017)01-0126-05

修回日期：2016-06-24