基于重复控制的单相PWM整流器偶次谐波抑制策略

刘俊杰，高曼曼，王月，江威风

（商丘学院电子信息工程学院，河南 商丘 476113）

基于重复控制的单相PWM整流器偶次谐波抑制策略

刘俊杰，高曼曼，王月，江威风

（商丘学院电子信息工程学院，河南 商丘 476113）

PWM整流器具有网侧功率因数高和电流畸变小的特点，但实际中电网电压的畸变及死区等多种非线性因素可能导致并网电流畸变甚至含有偶次谐波。将基于内模原理的重复控制器应用到单相PWM整流器的控制中，利用其在谐波频率处高增益的特点提高并网电流质量。推导了单相PWM整流器的平均开关模型，并分别基于经典控制理论和最小增益原理介绍了比例系数和重复控制器的参数整定过程。最后搭建了实验样机验证了该控制策略的有效性。

脉宽调制整流器；内模原理；重复控制；谐波抑制

PWM在整流器上的应用是整流技术的一次革命，是电动汽车充电电源后级DC/DC变换器的重要环节。基于PWM的整流技术可以实现网侧电流单位功率因数并具有极小的总谐波畸变率。但实际应用中桥式电路普遍存在的死区效应可能导致并网电流过零钳位，若电网电压存在畸变，会严重影响到并网电流质量。PI控制器可以实现直流参考的零静差跟踪，但PWM整流器并网电流为正弦量，采用PI控制器会存在稳态静差。PR控制器可以实现谐振点处正弦量的零静差跟踪，所以被广泛用在并网逆变器控制中，但为了抑制并网电流的谐波电流，需要使用多个PR控制器并联的结构［1］，这将降低系统的稳定裕度，随着并联PR数量的增加可能导致系统失稳，所以一般需采用一定的补偿措施，增加了控制器设计的复杂程度，而且，一般只增设奇数次谐振频率，未能兼顾对偶次谐波的抑制作用。

基于内模技术的重复控制器在换流器控制中得到广泛的应用［2］，通过对交流信号的周期积分实现对周期信号的跟踪。由于重复控制器在工频的整数倍频率下均具有较高的增益，所以对周期信号有较强的跟踪能力。由控制理论可知，由于重复控制器在奇数及偶数次谐波处均具有较高的增益，所以对周期性扰动同样具有较强的抑制能力。重复控制本质上属于延迟控制，所以响应速度较慢，为了保证系统的快速性，一般和比例控制器并联使用。比例控制器在误差出现时及时进行调节，保证系统的快速性，重复控制则通过对交流信号误差的积分提高稳态时网侧电流的质量。

1 原理与设计

1.1 PWM整流器的平均开关模型

图1所示为单相PWM整流器主电路。

图1 单相PWM整流器主电路Fig.1 Main circuit of the single-phase PWM rectifier

图1中，L为并网滤波电抗器，R为滤波电抗器的等效电阻，Lg为电网等效电感，Rg为电网等效电阻，uinv为PWM整流器交流侧逆变输出电压，由图1可得如下关系：

定义开关函数：

则PWM整流器交流侧逆变输出电压和直流电压可分别表示为

将式（3）代入到式（1）可得：

由式（4）和式（5）可得系统的状态空间方程为

若式（6）中所有的物理量取为1个开关周期的平均值，则式（6）可被看作系统的平均开关模型。可见，通过控制开关函数可以对电路中的直流电压和电感电流等物理量进行控制。由式（3）和式（6）可得单相PWM整流器的控制框图如图2所示，为了减小装置启动时的冲击，改善装置启动性能，这里引入了电网电压前馈。

图2 PWM整流器电流控制框图Fig.2 Control diagram of the PWM rectifier

1.2 重复控制器设计

重复控制通过对周期信号的积分实现对周期信号的跟踪。为了保证系统的稳定性，重复控制器通常包含一些校正环节，共同构成重复控制模块，对应的框图如图3所示。

图3 重复控制模块Fig.3 Repetitive control module

图3中，Kp为比例系数，该比例通道为了保证系统的快速性。q(z)为一常数或低通滤波器，主要是为了提高系统的稳定性，通常较小的q(z)对应着较慢的积分速度，但可以保证系统有较大的稳定裕度，所以q(z)可以在保证系统稳定性要求的前提下取较大值。k为超前校正步长，主要为了校正由数字控制、s(z)及控制对象引入的相位滞后。kr为保证重复控制模块稳定性的幅值增益。s(z)通常设置为低通滤波器以便对通道内的高频分量进行衰减，实现幅值镇定，提高系统的稳定性。

由图3可知重复控制模块的传递函数为

控制对象在离散域的数学模型表示为Gp(z)，则由图2可知整个系统的误差传递函数可表示为

当控制频率足够高时，可以忽略PWM环节造成的延迟，即取GPWM(z)=1，将式（7）代入到式（8）可得：

由式（9）可得整个系统的误差传递框图如图4所示。

图4 系统的误差传递框图Fig.4 Block diagram of the system error

可见，如果要保证系统稳定，则需要保证图4中3个环节T1(z),T2(z)和T3(z)分别稳定，T2(z)中q(z)通常取稍小于1的常数，这里取0.95［3］，所以T2(z)稳定。T1(z)可以按照只采用比例控制时进行整定，T3(z)为1个正反馈环节，若令

根据最小增益原理，T3(z)稳定的充分但非必要条件为|H(z)|＜1。

以下的仿真和实验研究中所采用的主电路参数为：输入电压Ug=220 V，额定电流Io=100A，采样频率fs=9.6 kHz，滤波电感L=0.25 mH，直流侧电容C= 470×6 μF，直流电压Udc=400 V。为了减小纹波电流在电容器上引起的发热，直流侧滤波电容采用6个电容并联的结构。取kp=1.5，则只采用比例控制时系统的开环Bode图如图5所示，系统截止频率取约1/10开关频率，此时系统的相位裕度为72°。

图5 比例控制时系统开环Bode图Fig.5 Bode diagram of the proportional control system open transfer function with onlykp

取超前校正步长k=2，幅值校正kr=0.6，s(z)为二阶低通滤波器，截止频率取1 kHz，品质因数为0.707，则可得H(z)的Nyquist图如图6所示。可见，H(z)的模值位于单位圆内，即满足|H(z)|＜1，重复控制环稳定。需要指出的是，考虑到实际系统中PWM装载造成的一拍滞后，实际的超前校正步长取3。

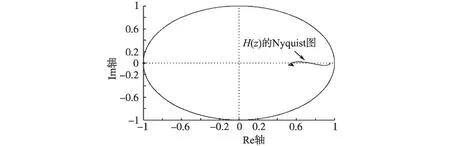
图6H(z)的Nyquist图Fig.6 Nyquist plot ofH(z)

1.3 谐波抑制能力分析

图7所示为采用重复控制时系统的开环Bode图。由图7可知，系统在奇次和偶次谐波频率处均具有较大的幅值增益［4］，所以重复控制器具有对奇次和偶次扰动的抑制能力。

图7 采用重复控制时系统开环Bode图Fig.7 Bode diagram of the repetitve control system open transfer function withkpand RC

2 实验验证

为了验证基于重复控制的单相PWM整流器偶次谐波抑制性能，搭建了单相PWM整流器样机，样机参数同主电路参数。由图3所示的重复控制模块原理图可知，重复控制中主要包含了纯延迟单元，其中q(z)z-N为1个周波的延迟，这在数字控制中可以通过将前一周波信号循环存储在相应长度的数组中，然后取当前时刻的前N时刻数据来实现，后面的z-(N-k)则可通过取前N-k时刻的数据来实现。低通滤波环节s(z)则按照相应的差分方程实现。为了便于比较，这里同时给出了采用多PR并联控制（只并联奇数次）时的实验结果。两种控制策略时网侧电流如图8所示。

图8 网侧电流Fig.8 The grid-side current

当系统中存在偶次谐波干扰时，采用PR控制时由于未加入相应的谐振环节而不能被有效抑制，网侧电流正负半周不对称，存在偶次谐波，采用重复控制时网侧电流得到明显改善。图9显示采用重复控制后网侧电流的寄次和偶次谐波均进一步减小，网侧电流ΤHD从5.27%降低到1.56%。

图9 网侧电流THDFig.9 THD of the grid-side current

以上结果表明重复控制可以显著改善整流器稳态并网电流质量。为了比较该控制策略下系统的动态性能，图10和图11分别给出了采用多PR并联控制和重复控制时给定电压和负载电流突变时的动态波形。可见，两种控制策略下系统的动态特性基本相同，这是由于系统的动态特性由系统带宽决定，而两种控制策略下系统的带宽均主要由比例系数kp决定，在两种控制策略下均按照穿越频率为1/10开关频率确定kp,所以动态特性基本相同。

图10 输出电压变化动态过程Fig.10 Dynamic process when the output voltage step changes

由以上实验结果可知，该控制策略在不影响系统动态特性的基础上可以有效地抑制诸如电网电压畸变和死区等因素对并网电流的影响。对于低压配电网，尤其是弱电网来讲，电网电压质量一般较低。由于功率限制，单相PWM整流主要应用在低压场合，此时采用重复控制可保证装置在电网电压质量较低时网侧电流畸变率仍能满足相关标准，应用前景广阔。

图11 负载电流突变动态过程Fig.11 Dynamic process when the load current step changes

3 结论

在进行控制器参数设计时可以对比例和重复控制分别进行设计。由于重复控制导致系统误差传递中含有正反馈项，一种简单且有效的环路稳定充分条件为重复控制正反馈通道的增益小于1。基于重复控制的单相PWM整流器具有对环路上奇次和偶次谐波的抑制能力，可以有效提高网侧电流波形质量，理论和实验验证了该控制策略的有效性。

［1］陈建国，曾斌.基于多重PR控制的LCL型逆变器谐波抑制［J］.电力电子技术，2015，49（4）：91-93.

［2］赵涛，王吉虎，黄家才，等.基于PI和重复控制三相并网逆变器的设计［J］.电力电子技术，2015，49（1）：20-22.

［3］Cho Younghoon，Lai Jih-sheng（Jason）.Digital Plug-in Repeti⁃tive Controller for Single-phase Bridgeless PFC Converters［J］.IEEE Trans.on Power Electronics，2013，28（1）：165-175.

［4］Trinh Quoc-nam，Lee Hong-hee.An Enhanced Grid Current Compensator for Grid-connected Distributed Generation un⁃der Nonlinear Loads and Grid Voltage Distortions［J］.IEEE Trans.on Industrial Electronics，2014，61（12）：6528-6537.

Even-order Harmonic Suppression Strategy for Single-phase PWM Rectifier Based on Repetitive Control

LIU Junjie，GAO Manman，WANG Yue，JIANG Weifeng
（Electronic Information Engineering College，Shangqiu University，Shangqiu 476113，Henan，China）

PWM rectifier has the characteristics of low current distortion and high power factor in the grid side，however many nonlinear factors in the practice such as the distorted grid voltage and dead time may produce some distortion and even-order harmonics in the grid-side current.The repetitive controller（RC）based on internal principle was used for controlling single-phase PWM rectifier，and its high gain at the harmonics was used for improving the quality of the grid-side current.The average switch model of the single-phase PWM rectifier was elicited，and the parameters setting method for proportionality coefficient and repetitive controller was introduced based on the classical control theory and small-gain theorem respectively.Lastly，a prototype was built and the experimental results confirm the validity of this strategy.

pulse width modulation rectifier；internal principle；repetitive control；harmonic suppression

TM461

A

10.19457/j.1001-2095.20170207

2015-12-21

修改稿日期：2016-06-15

河南省商丘市科技攻关计划资助项目（131021）

刘俊杰（1984-），男，硕士，讲师，Email：ljjemail@163.com