一种页岩体积压裂复杂裂缝的量化表征

尚校森，丁云宏，卢拥军，王永辉，杨立峰

[1.中国石油大学(华东)，山东 青岛 266580； 2.中国石油 勘探开发研究院廊坊分院，河北 廊坊 065007]

一种页岩体积压裂复杂裂缝的量化表征

尚校森1，丁云宏2，卢拥军2，王永辉2，杨立峰2

[1.中国石油大学(华东)，山东 青岛 266580； 2.中国石油 勘探开发研究院廊坊分院，河北 廊坊 065007]

基于典型页岩压裂复杂裂缝分布形态，在考虑裂缝复杂程度、裂缝分布和裂缝对产量贡献的基础上，建立了复杂裂缝表征方法，提出了裂缝潜能指数的概念，作为定量对比复杂裂缝优劣的参数之一。使用上述裂缝表征方法计算裂缝在距离改造点不同位置处的分布密度，以判断裂缝系统的增产有效性。根据4种典型裂缝分布形态的表征结果，相对于裂缝分布曲线先缓慢上升后急剧增加的内疏外密裂缝系统，分布曲线先急剧增加后缓慢上升的内密外疏的裂缝增产效果更好。开展了页岩水力压裂物理模拟实验，进行了裂缝形态表征对比。结果表明，与高水平地应力差条件相比，低水平地应力差下形成的裂缝网络的潜能指数和单位复杂程度对应的潜能都明显较大，说明低水平地应力差下的裂缝网络具有较大的提高产量潜力。研究结果显示，建立的裂缝表征方法综合体现了裂缝复杂程度、裂缝分布特征和裂缝对产量的贡献，可用于评价和描述页岩压裂复杂裂缝的增产有效性。

潜能指数；定量表征；体积压裂；复杂裂缝；页岩

页岩水力压裂物理模拟实验结果显示页岩压裂可以产生复杂裂缝网络[1-2]；现场微地震监测结果表现为信号范围大、破裂信号强，由测斜仪结果判断压裂后裂缝既有垂直缝也有水平缝，故页岩气经压裂形成的裂缝系统复杂[3-5]，但复杂裂缝定量表征困难，在实际压裂设计与模拟中无明确表征方法，限制了方案间的对比与优选，阻碍了压裂设计的优化和改进。

页岩储层页理及天然裂缝等结构弱面发育，脆性较大，水力压裂裂缝与页理、天然裂缝相互作用形成具有一定复杂程度的裂缝网络[6-8]。现有裂缝描述方法有线密度、面密度、分形理论和基于微地震监测的方法等，合理描述压裂裂缝的扩展形态和复杂程度是压裂优化设计的依据之一[9]。C.L.Cipolla等[10]最初建立了常规储层压裂裂缝复杂性指数表达式：微地震监测的缝长与缝宽之比。在此基础上，蒋廷学等[11]建立了水平井分段压裂裂缝复杂性指数，其引入了缝高延伸因子、缝长延伸因子、缝间干扰因子及非平面扩展因子。随后该方法又得到进一步的深化[12]，考虑各分支裂缝沿主水力裂缝方向的分布密度及其相互间渗流干扰波及面积。合理描述压裂裂缝形态复杂程度是建立页岩压裂模拟实验评价标准的基础。郭天魁等[13]引入了压后裂缝结构面迹长分布的分维值，结合面密度对裂缝网络进行定量表征；P.Riley等[14]也利用分形理论引入关联维数与最大Lyapunov指数。侯冰等[15]在水力裂缝沟通体积的基础上提出了利用“裂缝沟通面积”(SRA)作为水力压裂效果的评价指标，按照液体沟通程度划分等级取值求和。M.Balzarini[16]验证了核磁研究岩石裂缝孔隙的可行性。Z.Conny等[17]研究了一种裂缝网络评价程序，耿飞等[18]开发了裂缝图片分析软件。本文在充分利用已有方法并结合多个参数的基础上建立复杂裂缝表征方法，将裂缝复杂程度、裂缝分布与其对产能的贡献联系起来，以期更形象更直观地进行裂缝表征。

1 基本模型的建立

建立如图1所示的4种典型具多层理发育特征的压裂裂缝分布形态，分别记为模型A、模型B、模型C和模型D，其中横线代表页岩广泛发育的水平层理，与之相交的线代表水力裂缝或天然裂缝，三者相互连通相互作用形成了具有一定复杂程度的复杂裂缝系统。

页岩页理、天然裂缝和水力裂缝的渗透性高于基质页岩，可认为是气体流通的主要通道。考虑多水平页理通过天然裂缝和水力裂缝相互连通并提供气体流向井筒的通道，简化页理之间的连通裂缝为直线裂缝，则裂缝的角度不同，疏密分布不同，可通过多参数多角度进行描述，首先进行裂缝稀疏分布的表征。

2 裂缝分布表征

裂缝面密度为单位面积内裂缝的长度，为裂缝累计长度与横截面上基质总面积的比值。将分形理论中的码尺法应用到面密度的求取中，既可以得到裂缝面密度值，又可得到裂缝的几何分布及其对产能的贡献分析。具体做法：首先，以压裂改造点或改造点的投影点(当截面不通过改造点时)为圆心，以长度r为半径作圆，计算该圆形区域内的裂缝面密度；逐步改变圆半径r值，计算相应的裂缝面密度值，就可得到一系列的裂缝面密度值及其所对应的半径区域，将计算结果绘制在坐标系中，就可以看到裂缝面密度值随半径r的变化趋势，即裂缝在距离改造点不同距离处的分布(图2)。此处裂缝面密度采用网格覆盖法中裂缝所占的网格数表示，即半径为r的圆中含有裂缝的网格的数目，四种典型裂缝网络系统(图1)所对应的裂缝分布结果如图3所示。

图3a显示随着圆形区域半径r增大，含有裂缝的格子数呈均匀增加，说明模型A裂缝分布均匀，不存在稀疏和稠密之分，末尾处r为6时，格子数增加不明显，是因为此时圆形区域达到边缘处，边缘处裂缝很少。图3b显示，随着r的增大，裂缝格子数也均匀增加，但增加幅度大于模型A。说明图3b所对应裂缝系

图1 4种典型网络裂缝模型Fig.1 Four typical complex fracture modelsa.模型A;b.模型B;c.模型C;d.模型D

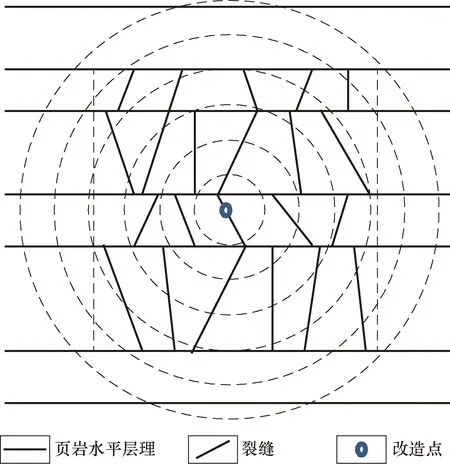
图2 裂缝分布表征示意图Fig.2 Schematic diagram of characterizing the distribution of fractures

统裂缝模型B比较稠密，可以较好的沟通储层，增加气体流动，但如果裂缝过于稠密，改造成本也相应较大，其增产油气量或许达不到经济值。图3c显示，当r较小时，裂缝格子数很少，当r增加到一定程度时，格子数突然增多，拐点明显(r=r0)，说明模型C改造点附近裂缝较少，裂缝稀疏，距离改造点r0以外的区域裂缝较为稠密，所以格子数较多，裂缝网络类型为内疏外密型。图3d显示，格子数随r的变化也存在拐点(r=r0)，但变化趋势则与模型C相反，在r小于r0范围内，裂缝所占格子数增加较快，说明近改造点区域裂缝稠密。r大于r0之后，格子数增加缓慢，说明远离改造点区域裂缝稀疏，裂缝集中分布在改造点附近区域，裂缝网络类型为内密外疏型。相比之下模型D更加有利于沟通储层与井眼，因为模型C的裂缝主要分布于远离井眼的区域，与井眼连通性不好，不利于储层流体流向井底。

3 分形维数与裂缝潜能指数

3.1 复杂裂缝分形维数的计算

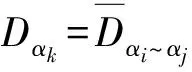
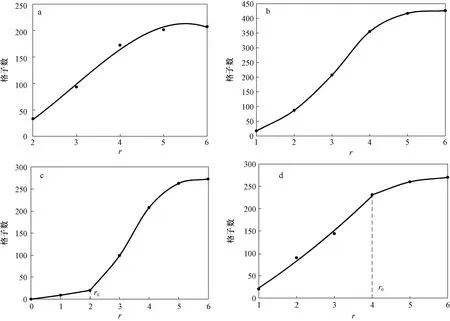
图3 裂缝分布表征曲线Fig.3 Curves of fracture distributiona.模型A;b.模型B;c.模型C;d.模型D

图4 网格划分与分形维数计算Fig.4 Meshing and caculating the fractal dimension

(1)

lgNb=lgM-Dlgb

(2)

式中:b为网格边长，无因次；M为裂缝分布初值，无因次；D为裂缝网络的分形维数，无因次。

以模型A(图1a)为例，计算其分形维数方法及结果如图4所示。可知，模型A裂缝系统分形特征明显，直线相关性较好，其分形维数为1.607。

3.2 不同角度或角度区间裂缝的产能贡献比

选取典型角度值α：0°,15°,30°,45°,60°,75°和90°，建立如图5所示裂缝模型，分别对其进行产能模拟[20]，得出产量比q(水平井产能与对应直井开发时产能之比)随角度的变化趋势。并以夹角为α为0°时对应的产量比q0°为基数，计算不同角度裂缝对应的产能贡献比：Rα=qα/q0°，回归得出对应关系。为了使计算更易操作，可计算αk所在角度区间的产能贡献比，其取值为两个端点角度值对应产能贡献比R的算术平均值：

(3)

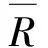
由张凤喜[21]的电模拟结果，产量贡献比随角度的变化如图6所示，拟合公式得产能贡献比与角度的变化关系。

(4)

式中:Rα为裂缝产能贡献比函数，无因次；α为裂缝的角度值，(°)。

以15°为步长划分0～90°为6个角度区间，每个角度区间对应的产能贡献比取值为区间两端点值的算术平均，结果如图7所示。可以看出划分角度区间之后的产能贡献比是呈阶梯式增加的，不但减小了取值的难度也使得计算更加快捷。

3.3 裂缝潜能指数

为了将裂缝系统复杂程度与其对产能的贡献联系起来，此处引入裂缝潜能指数。将上述裂缝复杂程度的表征参数分形维数D与产能贡献比R结合起来进行裂缝表征，提出如下两种方法。

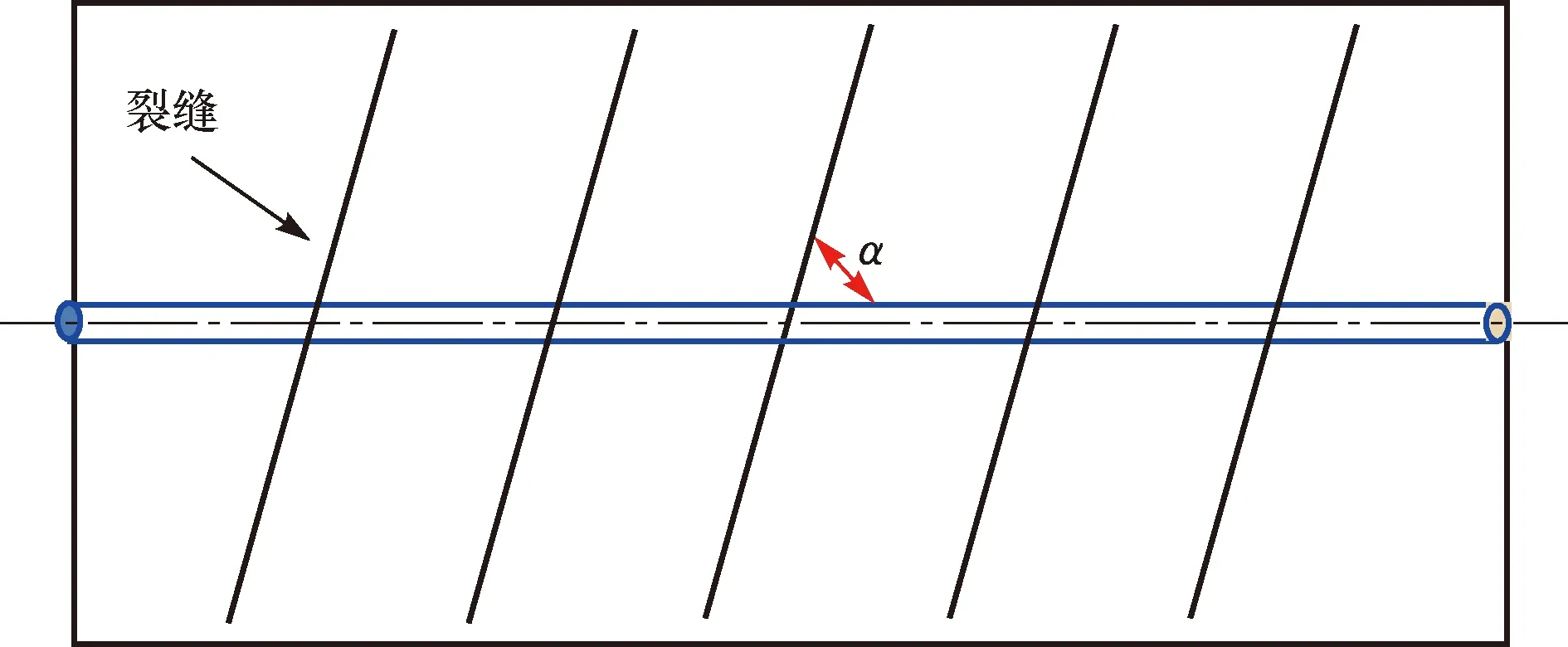
图5 夹角为α的裂缝示意图Fig.5 Schematic diagram showing fractures with an intersection angle of α

图6 产能贡献比随角度的变化Fig.6 Change of production contribution ratio with the increase of intersection angle

图7 不同角度区间裂缝产能贡献比取值Fig.7 Values of production contribution ratio under different intersection angle intervals

(5)

2) 将复杂裂缝系统范围内的每个角度区间([0°,15°)，[15°,30°)，[30°,45°)，[45°,60°)，[60°,75°)，[75°,90°])对应的裂缝分形维数，与该角度区间对应的产能贡献比(图7)做加权和，记为裂缝潜能指数FN。

(6)

由于精确到每一个角度的计算较为繁琐，以下采用方法2及其对应的裂缝潜能指数进行表征，以模型A为例进行计算，其对应的裂缝角度分布区间如图8所示，每个角度区间对应的分形维数和产能贡献(表1)，加权和即为该复杂裂缝系统的裂缝潜能指数FN。

由表1可知，模型A的裂缝潜能指数为3.21。以此类推可计算得出4个典型模型(图1)复杂裂缝系统所对应的分形维数及裂缝潜能指数(表2)。

由表2可知，模型A复杂裂缝网络的分形维数最小，说明其复杂度最小；模型B裂缝网络的复杂度最大；模型C和D的裂缝网络的分形维数接近，说明其复杂度也大致接近。裂缝潜能指数大小的排序为模型B,A,D和C，说明就增加产量效果而言，模型B裂缝网络优势明显。表2中最后一列为裂缝潜能指数与复杂度的比值F/D，可理解为单位复杂度所对应的潜能。模型B裂缝系统的分形维数和潜能指数大于模型A，说明压裂改造实现B裂缝的复杂度高，对产量增加贡献大，相应的改造成本也高，但是模型B裂缝网络的单位复杂度所对应的潜能F/D值较小，说明进行压裂改造实现模型B裂缝系统如此高复杂度在一些情况下是没必要的，改造形成模型A的裂缝系统已经可以较好满足增产及经济要求。裂缝D的内密外疏分布对产能有利，其FN值小于裂缝B但F/D值大于裂缝B，也说明了其优越性。

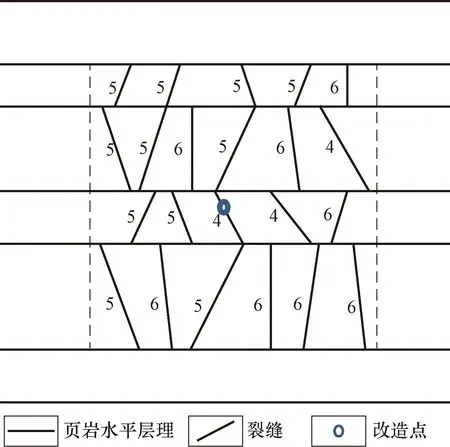
图8 裂缝潜能指数计算示意图Fig.8 Schematic diagram of potential index calculation4.处于角度区间45°～60°；5.处于角度区间60°～75°；6.处于角度区间75°～90°

夹角区间α/(°)RDFN445～601115056560～751139116675～901158109321

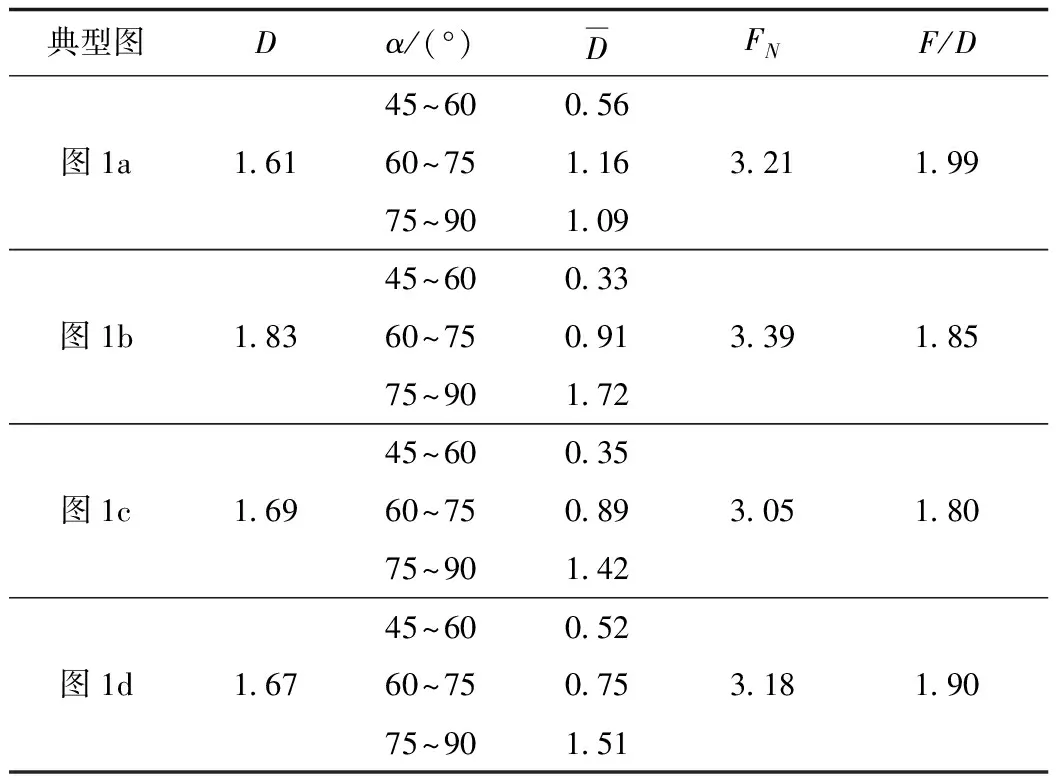
表2 分形维数与裂缝潜能指数计算结果

4 应用实例

页岩水力压裂物理模拟和数值模拟实验是认识和研究页岩气储层水力压裂特殊性以进行优化设计指导现场实际的两个重要手段，实验结果的对比分析是形成实验结论的关键。本部分通过两个实例说明上述复杂裂缝定量表征方法在水力压裂物理模拟和数值模拟中的应用，以有效进行实验结果的对比和分析。

4.1 物模实验应用

图9为两种水力压裂物理模拟实验条件下得出的两个不同的页岩岩心裂缝形态。图9a为低水平地应力差条件(3 MPa)对应的裂缝形态，图9b为高水平应力差(14 MPa)条件下的裂缝形态，粉红色线标示的为有压裂液显示的裂缝，为油气流动有效裂缝。以裂缝与井筒方向的夹角为依据划分裂缝所在角度区间，并标注序号。应用上述裂缝表征方法计算两种裂缝形态所对应的分形维数和裂缝潜能指数(表3)。

图9显示，两个裂缝网络系统中的裂缝处于多个角度区间，低水平地应力差下的裂缝所占夹角区间较多，相应高水平地应力差下的裂缝所占夹角区间较为单一。由表3可知，低水平地应力差条件下的裂缝网络的分形维数和高水平地应力差条件下的接近，说明从分形角度，两种裂缝网络复杂程度相近，但是低水平地应力差下裂缝网络的潜能指数FN和单位复杂程度对应的潜能F/D都明显大于高水平地应力差条件下的，说明低水平地应力差下的裂缝网络(图9a)具有较大的提高产量潜力。

图9 物理模拟实验后页岩岩心形成的裂缝形态Fig.9 Geometry of fractures in the shale sample after physical simulation experiment of fracturing1.处于角度区间0°～15°；3.处于角度区间30°～45°；4.处于角度区间45°～60°；5.处于角度区间60°～75°；6.处于角度区间75°～90°

序号α/(°)DDFNF/D图9a330～45074445～60066560～75094675～90098105375357图9b10～15093675～90096103214208

4.2 数模实验应用

图10为利用扩展有限元法模拟页岩水力压裂裂缝扩展的结果图，两图所示不同裂缝形态对应不同的杨氏模量分布。两个裂缝扩展路径复杂，所对应分形维数和裂缝分布如图11所示。

由图11可知，两个复杂裂缝网络的分形维数分别为1.132和1.099(图11a，b)，裂缝网络a的复杂程度要大于裂缝b。从裂缝分布来看，裂缝a扩展至上下两部分，随着圆形覆盖区域半径的增加，裂缝所占格子数均匀增加，当裂缝半径为5时，到达裂缝区域边缘，格子数目基本不变，边缘处裂缝较少，说明裂缝整体分布比较集中；裂缝b则趋于向下部扩展，随着半径增加，格子数增加幅度较裂缝a小，且到边缘区域无变缓趋势，说明其裂缝分布较裂缝a分布更为分散。

5 结论

页岩体积压裂复杂裂缝的定量表征方法是裂缝复杂程度、裂缝分布和对产量贡献的综合体现，用于评价和描述页岩体积压裂裂缝直观有效，操作简单。复杂裂缝具有分形特征，利用分形维数进行描述相关性较好；裂缝潜能指数结合了裂缝复杂程度及其对产能的贡献，可以作为定量对比复杂裂缝系统优劣的参数之一。裂缝分布表征可以直观得到裂缝在距离改造点不同距离处的分布密度，从而可根据裂缝稀疏分布判断裂缝系统增产有效性。

图10 数值模拟得出的裂缝网络形态Fig.10 Geometry of fractures from numerical simulation of fracturing

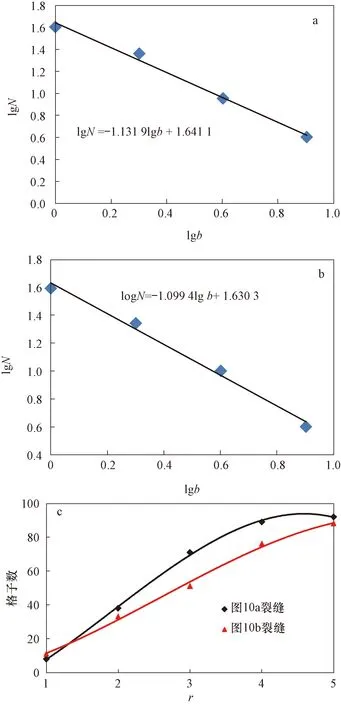
图11 裂缝分形维数和分布曲线结果Fig.11 Fractal dimension and distribution curves of facturesa.图10a裂缝的分形维数计算结果；b.图10b裂缝的分形维数计算结果；c.图10a和b的分布表征对比结果

[1] Guo T K,Zhang,S C,Qu Z Q,et al.Experimental study of hydraulic fracturing for shale by stimulated reservoir volume[J].Fuel,2014,(128):373-380.

[2] 衡帅，杨春和，曾义金，等.页岩水力压裂裂缝形态的试验研究[J].岩土工程学报，2014，36(7)：1243-1250. Heng Shuai,Yang Chunhe,Zeng Yijin,et al.Experimental study on hydraulic fracture geometry of shale[J].Chinese Journal of Geotechnical Engineering,2014,36(7):1243-1250.

[3] 王志刚.涪陵焦石坝地区页岩气水平井压裂改造实践与认识[J].石油与天然气地质，2014，35(3)：425-430. Wang Zhigang.Practice and cognition of shale gas horizontal well fracturing stimulation in Jiaoshiba of Fuling area[J].Oil & Gas Geo-logy,2014，35(3)：425-430.

[4] 钱斌，张俊成，朱炬辉，等.四川盆地长宁地区页岩气水平井组“拉链式”压裂实践[J]. 天然气工业，2015，35(1)：81-84. Qian Bin,Zhang Juncheng,Zhu Juhui,et al.Application of zipper fracturing of horizontal cluster wells in the Changning shale gas pilot zone，Sichuan Basin[J].Natural Gas Industry,2015,35(1):81-84.

[5] George E.King.Thirty years of gas shale fracturing:What have we learned?[C].SPE Annual Technical Conference and Exhibition.Florence,Italy,SPE 133456,2010.

[6] 赵立强，刘飞，王佩珊，等.复杂水力裂缝网络延伸规律研究进展[J].石油与天然气地质，2014，35(4)：562-569. Zhao Liqiang,Liu Fei,Wang Peishan,et al.A review of creation and propagation of complex hydraulic fracture network[J].Oil & Gas Geology,2014，35(4)：562-569.

[7] 周雁，袁玉松，邱登峰.泥页岩构造裂缝形成演化模式——以四川盆地东部泥页岩为例[J].石油与天然气地质，2015,36(5):828-834. Zhou Yan,YuanYusong,Qiu Dengfeng.A discussion on formation and evolutionary pattern of shale structural fracture:A case study of shale in western Sichuan Basin[J].Oil & Gas Geology,2015,36(5):828-834.

[8] 王志刚.涪陵页岩气勘探开发重大突破与启示[J].石油与天然气地质，2015，36(1)：1-6. Wang Zhigang.Breakthrough of Fuling shale gas exploration and development and its inspiration[J].Oil & Gas Geology，2015，36(1)：1-6.

[9] Warpinski N R,Mayerhofer M J,Vincent M C,et al.Stimulating unconventional reservoirs:Maximizing network growth while optimizing fracture conductivity[C]∥SPE unconventional reservoirs confe-rence.Keystone:SPE,2009.

[10] Cipolla C L,Warpinski N R,Mayerhofer M J,et al.The relationship between fracture complexity,reservoir properties,and fracture-treatment design[C]∥SPE Annual Technical Confernce and exhibition,21-24 September.Denver:SPE,2008.

[11] 蒋廷学.页岩油气水平井压裂裂缝复杂性指数研究及应用展望[J].石油钻探技术，2013，41(2)：7-12. Jiang Tingxue.The fracture complexity index of horizontal wells in shale oil and gas reservoirs[J].Petroleum Drilling Techniques,2013，41(2)：7-12.

[12] 蒋廷学，卞晓冰，袁凯，等.页岩气水平井分段压裂优化设计新方法[J].石油钻探技术，2014，42(2)：1-6. Jiang Tingxue,Bian Xiaobingl,Yuan Kai,et al.A new method in staged fracturing design optimization for shale gas horizontal wells[J].Petroleum Drilling Techniques,2014，42(2)：1-6.

[13] 郭天魁，张士诚，葛洪魁.评价页岩压裂形成缝网能力的新方法[J].岩土力学，2013，34(4)：947-954. Guo Tiankui,Zhang Shichengl.Ge HongkuiA new method for evaluating ability of forming fracture network in shale reservoir[J].Rock and Soil Mechanics,2013,34(4):947-954.

[14] Riley P,Tikoff B,Murray A B.Quantication of fracture networks in non-layered,massive rock using synthetic andnatural data sets[J].Tectonophysics,2011,505:44-56.

[15] 侯冰，陈勉，李志猛，等.页岩储集层水力裂缝网络扩展规模评价方法[J].石油勘探与开发，2014，41(6)：1-6. Hou Bing,Chen Mian,Li Zhimeng,et al.Evaluationor the propagation area of a hydraulic fracture network in shale gas reservoirs[J].Petroleum Exploration and Development,2014,41(6):1-6.

[16] Balzarini M,Nicula S,Mattiello D,et al.Quantification and description of fracture network by MRI image analysis[J].Magnetic Resonance Imaging,2001,19:539-541.

[17] Conny Z,Enrique G,Paul D,et al.Fracture network evaluation program(FraNEP):A software for analyzing 2D fracture trace-line maps[J].Computers & Geosciences.2003,60:11-22.

[18] 耿飞，解建光，钱春香.图像分析技术对混凝土裂缝的定量评价[J].混凝土，2005，5：78-82. Geng Fei,Xie Jianguang,Qian Chunxiang.Image analysis technique for quantitative evaluation of cracks in concrete[J].Concrete,2005,5:78-82.

[19] 朱华，姬翠翠.分形理论及其应用[M].北京：科学出版社，2011：37-42. Zhu Hua,JiCuicui.Fractal theory and its application[M].Beijing,Science Press,2011:37-42.

[20] 廉黎明，秦积舜，杨思玉，等.水平井渗流模型分析评价及发展方向[J].石油与天然气地质，2013，34(6)：821-826. Lian Limin,Qin Jishun,Yang Siyu,et al.Analysis and evaluation on horizontal well seepage models and their developing trends[J].Oil & Gas geology,2013,34(6)：821-826.

[21] 张凤喜，吴晓东，隋先富，等.基于电模拟实验的低渗透油藏压裂水平井产能研究[J].特种油气藏，2009,16(2)：90-95. Zhang Fengxi,Wu Xiaodong,Sui Xianfu,et al.Study on fractured horizontal well productivity for low-permeability reservoirs based on electric analogy[J].Special Oil and Gas Reservoirs,2009,16(2):90-95.

(编辑 张亚雄)

Quantitative characterization of complex fractures after volume fracturing in shale

Shang Xiaosen1,Ding Yunhong2,Lu Yongjun2,Wang Yonghui2,Yang Lifeng2

(1.ChinaUniversityofPetroleum(EastChina),Qingdao,Shandong266580,China; 2.LangfangBranchofResearchInstituteofPetroleumExploration&Development,PetroChina,Langfang，Hebei065007,China)

According to the typical geometry of complex hydraulic fractures of shale,a new method which takes the fracture complexity,the fracture distribution and the attribution of fracture to production into consideration was proposed to describe complex fractures.Moreover,the concept of fracture potential index was put forward,and it can be used as one of the parameters for quantitative evaluation of the complex fractures.The density of fractures with different distances from the stimulation location was estimated with the method for determining the effectiveness of the fracture network.Compared with the fracture network with the characteristics of being dense inside but sparse outside,the fracture network being sparse outside but dense inside is more effective in enhancing production according to the description results.Hydraulic fracturing experiments were conducted and the geometries of hydraulic fractures in the shale were described with the application of the method.Results show that the potential index of fracture network formed under low horizontal geostress difference is greater than that of fractures formed under high horizontal geostress difference.It reflects that the fracture network formed under low horizontal geostress difference has higher potential for enhancing production.The above results indicate that the method established for describing complex fractures can comprehensively reflect the fracture complexity,fracture distribution and attribution to production.It provides a mean for evaluating the effectiveness of complex hydraulic fracture network.

potential index，quantitative characterization，volume fracturing，complex fracture，shale

2015-10-07;

2016-12-20。

尚校森(1988—)，女，博士，油气藏增产改造。E-mail:shangxs2013@163.com。

中国博士后科学基金资助项目(2016M602226)；国家重点基础研究发展计划(973计划)项目(2013CB228004)。

0253-9985(2017)01-0189-08

10.11743/ogg20170120

TE122.2

A