基于ARIMA模型的沪深300指数预测及误差因素分析
李嘉松
(安徽大学 经济学院,安徽 合肥 230601)
基于ARIMA模型的沪深300指数预测及误差因素分析
李嘉松
(安徽大学 经济学院,安徽 合肥 230601)
本文使用Eviews软件建立ARIMA模型,对采样一年期的沪深300日数据进行数学处理,识别出建立模型的形式并且建立ARIMA模型,通过所建立的模型对沪深300指数进行预测.通过计量经济学方法评价预测质量,并根据实际预测结果,指出造成沪深300指数的实际值和模型预测值之间有差别的原因,为广大投资者提供沪深300指数的预测方法来作为未来进行股票投资和金融衍生产品投资的参考.
ARIMA模型;沪深300预测;误差;影响因素
1 引言
现行股票市场为了方便个人投资者或机构投资者把握市场风向,理性安排投资规模和投资组合,编制了多种类型的股票价格指数,如上证综指,深证成指,上证180和上证50等.沪深300指数由于其诸多特点受到广泛关注,沪深300所选用的成分股具有很高的稳定性,一般异常股票和新股不作为成分股,且由股票的自由流通量作为确定成分股权重的标准.综合这些特点,沪深300作为广大投资人进行金融投资决策的重要参考指标.
股票市场具有很强的不确定性,波动性,由于大部分的金融投资决策需要依赖于准确的市场预测,所以,如果能准确掌握未来的股票指数动向,就能在投资决策的过程中占据更多的主动权.对于预测沪深300指数,ARIMA模型是目前业界采用的比较多的方式.本文通过Eviews软件建立合适的ARIMA(p,d,q)模型,对沪深300指数的日指数进行预测.[1]
2 模型识别与建立
2.1 模型选择
本文的研究使用ARIMA模型,ARIMA模型是在ARMA(自回归移动平均模型)的扩展概念,将数据进行差分之后使得数据从非平稳数据变为平稳数据后再使用ARMA模型进行预测.当所选序列为平稳数列时,可以直接使用ARMA模型.
2.2 数据来源
本文通过选取2015年07月15日到2016年11月14日的沪深300的日数据(325个数据),数据来源为新浪财经,将这325个数据视为一个整年度的数据来处理(图1).
2.3 数据处理
为了减小序列的波动,现在对序列进行对数变换.对变换后的数列进行自相关和偏自相关分析,根据分析结果(图2)可以看出,对数数列的自相关分析图为非平稳序列.为了使用ARMA模型,需要对数列进行差分.采用分析自相关分析图来确定时滞数[2],决定对已经取对数的数列采取时滞数为(0,3)的差分,以消除其趋势性和季节性.之后对得到的新数列数据(图3)可以看出其观测值都在围绕某一值上下波动,振幅变化不剧烈,再次进行自偏相关分析,得到的结果(图4)可以看出序列已经基本平稳,然而偏相关分析图显示数据,季节性依旧明显,对该系列进行二阶季节差分,发现序列的这种季节性没有得到明显改善,故在此只进行一阶季节差分,即可以直接使用进行过一阶季节差分的数据建立ARIMA模型进行预测.
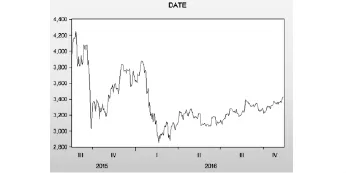
图1 沪深300日数据图(2014.11.26-2016.02.23)
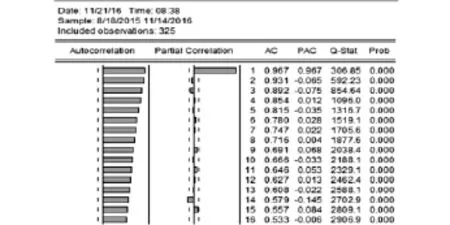
图2 取对数后新数据的自相关分析图
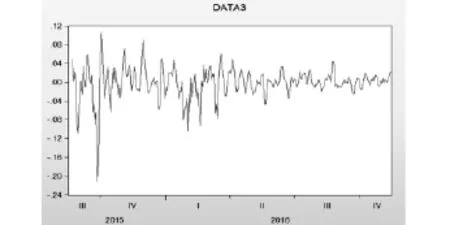
图3 对原数列取对数并进行时滞数为3的季节差分数据图
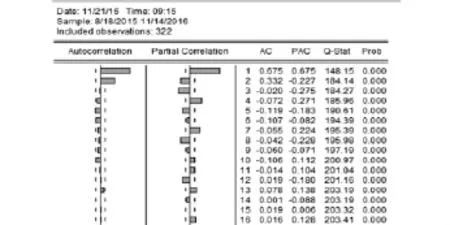
图4 经过季节差分之后的数据的自相关分析图
2.4 模型识别
在建立ARMA模型的过程中,可以通过自相关偏自相关图分析得到ARIMA(p,d,q)中的p和q的数值.根据AC (Autocorrelation)的截尾可以确定MA(q)中的参数q的值,而根据PAC(Partial Correlation)的截尾性可以确定AR(p)的参数p的值.从图中可以看出,AC与PAC均表现出截尾.可以根据PAC图确定AR(p)参数p为3,另外根据AC图确定MA(q)参数q为2.所以可以建立ARMA(3,2)的预测模型.
2.5 模型的建立
通过自相关和偏自相关分析图,可以确定模型参数,之后使用Eviews软件并且通过最小二乘法计算参数的估计量.以ARMA(3,2)建立模型.得到的参数估计结果如表5所示.根据输出的结果来看,模型的DW统计量略小于2,可以认定序列基本不存在序列相关,并且inverted AR/MA roots都在单位圆内,符合模型要求.模型的AIC指标和SC指标值都相对较低,综合调整之后的决定系数为0.72.可以认定模型的拟合程度较好.并且对该模型的残差序列进行白噪声检验,检验结果表面残差序列相互独立即为白噪声的概率很大,故不能拒绝序列相互独立的原假设.模型最终估计结果为:(1-0.016841B3)(1-0.177749B-0.605439B2-0.144559B3) (1-B3)Yt=(1+0.987507B3)(1-0.835345B-0.238111B2)Ut,其中Yt=log(X),X为沪深300当日收盘价;Ut为随机干扰项;B为滞后算子.
3 模型的预测应用
建立了模型之后,对Yt值进行预测,假设我们要预测2015年7月15日到2016年2月23日的沪深300收盘价格,我们使用Eviews软件完成模型的预测,采用动态预测(Dynamic).得到预测图如图6.把模型中预测的沪深300指数和实际的沪深300指数进行对比,可以通过该图看出,通过模型的预测,所能得到的预测值与实际值的差别在可接受范围内,并且从模型BP,TIC,MAPE等指标均可以看出模型预测的可信度和准确度也很好.把模型中预测的沪深300指数和实际的沪深300指数进行对比,给出整个样本期实际指数和预测指数对比,可以看出虽然模型中数据产生偏差有时候较大,但是总体对于趋势的预测是相对准确的.说明该模型的预测可以为投资者提供相对可靠的投资参考.
从模型预测显示的趋势看出,上证指数在目前阶段处于一个稳定的震荡期,虽然还没到达2014年的支撑线指数水平,但是有比较明显的稳中回升迹象,投资者应该保持一个审慎乐观的态度来观察后市动向,适时抓住入市机会.

图6 对目标期间指数的预测(预测DATAF与实际收盘价DATA的对比)
4 预测偏差分析
通过预测曲线和实际沪深300指数的对比可以发现,实际值和预测之间的差额有时会产生很大的偏差,偏差的一方面原因来源于ARIMA模型本身的局限性和设定过程中由于简化模型所产生的误差.而另一方面就要寻求指数本身受外界因素的影响[3].
在通过ARIMA模型设定模型产生误差中,可以理解为产生误差的因素来自于外生的偶然性变量,众所周知,沪深300反映了在上交所和深交所上市的权重股票的股价变动情况,而股价主要收到下列几个方面的影响,市场前景,经济状况,企业发展前景,投资者心理等,但是,由于我国股市起步晚,各方面体系还不稳定.下面着重分析影响指数的非经常性因素[4].
4.1 政治性因素
由于我国政府的政策对经济的导向能力较强,所以政府对于政策的发布取消和法律文件的修改都会对股市的未来走向产生巨大的影响,这种影响一方面来自于政令本身对于股市波动的直接作用,另一方面就是对投资者的心理影响产生的间接作用,让投资者对未来产生利好后者利空的情绪,并且这种情绪是会相对放大的.一般有预告性的政策不会使得股市产生突然性波动,但是颁布过程有一定突然性的政策,会使得股市产生非自然的剧烈波动,个股的普遍波动,就会反映到沪深300指数上,体现为指数的不可预测的波动.
虽然说政府政策对于股市波动的影响是在世界各国普遍存在.但是在中国,政策的影响有一些特点.首先,中国政府政策对于经济运行的影响相对其他国家都要更加强烈和有效,政府的公信力和对于经济的控制能力是在各国政府中较为出众的,所以有中国政府颁布的政策法规对人们的心理影响是非常大的,人们会做出超出理性范围内的应对反映,从微观上表现为大量的买入和卖出,宏观上则表现为股市巨量波动.其次,中国政府的经济首要目标是经济的稳定发展,也就是说经济的稳定是第一要务,所以政府政策也会配合这种目的,当股市有大涨大落的趋势的时候,政府往往会出台逆经济形势的政策使得经济回到相对稳定的路线上.所以可以看出当故事出现剧烈波动后,往往接下来会进入一个相对稳定时期,而模型本身很难预料到这种偶然因素的影响,这也就是误差产生的一个原因.
4.2 节假日因素
由于我国股票交易制度,周六,周日和节假日等均是休市期,本身休市并不会对股票市场产生影响,但是从实践中来看,我国经常在周五和周一以及节假日两端的交易日产生于总体趋势不相符的波动.这是由于在休市期间,一旦颁布一些新政策,会让下一个交易日产生巨大波动,人们处于自身稳健性投资的需要往往要回避这种风险,所以往往选择在节假日前放弃持股.这种行为更多来自于人们心理的影响.所以这也是解释实际值于预测值之间区别差别的原因之一.
4.3 指数编制技术因素
沪深300指数相比于上证综合指数来说,对于指数内成分股有着自己独特的选择条件.首先刚刚上市的股票和ST股票是不会被选为成分股的,也就是说当一个股被从普通股调整为ST股之后,可能就会丧失了进入成分股的资质,被从原编制体系中剔除.在这个过程中,沪深300股指也会由于这种偶然性因素产生波动,但是相比于上面两个因素,这个因素对于实际股指偏离预测值的贡献要小很多,因为沪深300正是由于需要保持相对的稳定性,不受个股影响等才编制了这些规定[5],所以指数编制本身的波动是很小的.
5 结束语
由于沪深300指数具有非平稳性,时序性,随机性等特点,使得其可以使用ARIMA进行预测,但是也是由于沪深300指数受人们主观投资心理影响较大,季节性表现不明显,所以在建立模型的过程中很难完全消除序列的非平稳性,为了简化模型,也往往像本文一样将P和q参数的值取相对较小.虽然简化了模型,但是由于本文模型在选用数据过程中是直接先对原始数据取对数在直接进行季节差分,用处理过的数据再用于模型建立预测,尽可能保留了重要信息,根据拟合结果和预测指标来看,也能作为投资者投资活动中的重要参考.
〔1〕赵志峰.对建立中国股票价格指数时间序列模型的探讨[J].统计与信息论坛,2003(1).
〔2〕刘冰.沪深300股指期货期现套利中现货选择研究[J].时代经贸(中旬刊),2007(SC).
〔3〕白营闪.基于ARIMA模型对沪深300指数的预测分析[D].华南理工大学,2010.
〔4〕冯予,陈萍.非线性时间序列分析在股市行情预测中的应用[J].南京理工大学学报,1998(01).
〔5〕陈晶鑫.基于灰色模型和ARCH模型对股价指数的实证分析[D].东北财经大学,2007.
〔6〕Chung,Y.P.A TransaetionsDataTestofStoek Index Futures Market Effieiency and Index Arbitrage Profitability.The Journal of Finance.2007.
〔7〕李春晓.基于ARIMA模型的股票市场并购套利异常收益的研究[D].云南师范大学,2014.
〔8〕徐绪松,马莉莉,陈彦斌.我国上海股票市场GARCH效应实证研究[J].武汉大学学报(理学版),2002(03).
〔9〕李扬.ARIMA模型对我国寿险业潜在保费的预测研究[D].湖南大学,2006.
〔10〕张数京,齐立心时间序列分析简明教程[M].北京:清华大学出版社,2003.
F830.91
A
1673-260X(2017)01-0073-03
2016-10-03

