电能数据采集用户终端谐波分析及计量改进方法

伍少成，王 政

（1.中国南方电网公司深圳供电局 广东 深圳518000；2.烟台东方威思顿电气股份有限公司 山东 烟台264000）

电能数据采集用户终端谐波分析及计量改进方法

伍少成1，王 政2

（1.中国南方电网公司深圳供电局 广东 深圳518000；2.烟台东方威思顿电气股份有限公司 山东 烟台264000）

智能电表是目前最具应用前景的电能数据采集用户终端。为了改善电网谐波污染，提升电能质量。首先采用快速傅里叶变换计算了谐波分析的运算效率，提出了复序列分裂基谐波分析方法，提高了谐波分析的运算效率。采用基于三角自卷积窗的电能计量改进方法对频域特性进行仿真分析。研究表明：基于三角自卷积窗的电能计量方法对有功功率的计量精度明显高于典型的窗函数，比Nuttall窗函数的计量精度高1～2个数量级。

智能电表；谐波分析；计量方法改进；三角自卷积窗；复序列分裂基

自2010年开始，国家电网开始大范围普及智能电表。到目前，智能电表普及率已经达到80%以上，显著提升了全国电网信息采集效率[1]。根据规划，中国电网需要在2020年之前将智能电表普及率提升至100%。因此可以预见，智能电表将在为广大用户带来用电便利的同时，也会有效降低电网运行成本，并推动改进电网服务质量。

在电学领域，谐波是指电流/电压中基波频率整数部分[2]。在电能计量过程中，如果电信号非工频（50 Hz），则被视为谐波。电网中一旦产生谐波，会破坏正弦电压的常规波形，导致电能异常损耗并可能进一步引发输送电系统故障。在输送电中，如果谐波超过本线路总电压的30%，则会破坏负载平衡，发生集肤效应[3]。此时，如果不及时采取措施，就会对中性线施加电流，从而发生严重电力事故，如发电机跳闸、大面积停电等。根据国家电网公司数据，谐波因素引发的电力事故每年造成共约30亿元经济损失。若其它次生灾害计算在内，损失将更严重。可见，谐波问题对电网运行所形成的危害不可忽视[4-5]。

在智能电表使用过程中，如果要有效应对谐波危害，须首先做好谐波计量和分析工作。基于用户终端，拟对谐波进行傅立叶变换DFT分析、分裂基FFT算法（即SREFT算法）分析；进一步地，就如何改进谐波计量进行算法讨论和仿真分析。相关分析和讨论一方面可以为提升电能计量精确性提供依据，并督促电网向用户提供更高质量电能；另一方面也可以为电力设备性能评估提供基础参考。另外，对谐波进行精确测量还可以为输送电系统的无功补偿方案提供数据支持，并协助电网做好系统故障预警。

1 谐波分析及SRFFT算法

1.1 快速傅立叶变换

1.1.1 DFT方法局限性

从理论上看，快速傅立叶变换DFT方法在有限长序列中较为适用，如果抽样点N较大或者序列无限长，则会存在计算难度过大的显著局限性。

对有限长序列x（n），其DFT变换公式为[6]：

如果对序列x（n）进行IDFT变换，则有[7]：

1.1.2 FFT算法

为应对DFT方法局限性，FFT算法可以对长序列进行分解，从而有效控制计算量。在实际应用时，FFT算法被分为DIT基-2算法、DIF基-2算法以及实序列FFT算法等。其中，DIT基-2算法应用范围较广，应用效果也较为理想。如图1所示，为DIT基-2算法变换过程示意图。

图1 DIT-FFT变换示意

如表1所示，在运用FFT算法的具体过程中，需要注意运算次数控制。

从表1可知，随着采样点N上升，各类FFT算法乘法/加法次数也相应增加；各采样点水平下，各类FFT算法运算次数要显著低于DFT算法。本研究中，后续分析采样点为128。在各类算法中，SREFT算法运算次数与基-2算法不相上下，然二者运算时间分别为0.05 s、0.06 s。综合考量，本研究选择使用SREFT算法。

表1 FFT算法的实数乘法/加法次数统计

1.2 谐波分析的SRFFT算法

分裂基FFT算法（即SRFFT算法）包括如下6个基本步骤[8-9]：

1）奇数组及偶数组分组。

假设采样点N=2m，m为整数，则通过下式对序列{u（n）}分作划分处理：

2）划分子序列。

对偶数组、奇数组分别运用基-2FFT算法、基-4FFT算法，可得下式所示子序列：

3）对式（1）作离散傅立叶变换。

4）第一级分解流程。

如图2所示，通过上述推导步骤，可得复序列分裂基DIY-FFT算法第一级分解流程[12-13]。

图2 复序列分裂基算法第一级分解流程

5）计算蝶形数目

结合图2可知，如果采样点N=2m，那么其分解流程就包括m个步骤。对于第l级步骤而言，其蝶形计算可按下式进行[14-15]：

对于第l级，若欲求取其倒L型蝶形数目，可按下式进行：

进一步地，可按下式计算倒L型蝶形总数：

6）获取运算次数。

对于三阶分裂基FFT算法而言，可按下式求取运算次数：

从以上分析可知，SREFT算法具有运算量少、计算过程简单、内部数据结构清晰的优点。在运用过程中，SREFT算法的序列排列较为简单，很容易实现二进制编码，从而便于借助已有计算机程序或者进行对象开发。

2 电能计量及改进方法

2.1 窗函数的选择

目前，被证实比较成熟的窗函数有Rectangle函数、Triangle函数以及Nuttall函数等。如表3所示，为常见窗函数及其旁瓣特性。

表3 常见窗函数及其旁瓣特性统计

由表3可知，综合无精度参照物、旁瓣衰减速率、精确信号分析等方面标准，Hanning窗函数具有相对理想的电能计量性能，其谐波表达式为：

式中，N表示采样点数目；a表示参照系数，通常情况下取0.5。

需指出的是，通过Hanning窗函数来对电信号进行傅里叶变换分析确实可取得有较好效果。然而，在智能电表运行过程中，不可忽视谐波的存在。因此在进行变换分析的过程中，需要运用三角自卷积窗函数TSCW来对谐波特性进行分析，并探讨谐波控制方案。

2.2 三角自卷积窗频域特性

2.2.1 TSCW频域特性

结合FFT理论及卷积定理可知，由TSCW离散频谱函数可得其p阶响应幅值函数，其计算公式如下：

对式（12）而言，若k=2 pm，则Wp（k）=0。此时，若m=1，k=2p，则可得频域原点。在频域原点，存在最低程度频谱泄露水平，且零值点与频域原点之间存在4pπ/N的距离。于是，可得p阶TSCW的主瓣宽度BW：

由式（13）可知，当TSCW采样点固定时，卷积阶数p与M值呈反比例关系，与主瓣宽度Bw呈正比例关系。进一步地，可求得卷积阶数p、TSCW旁瓣衰减速度D以及旁瓣电平最大值之间存在的近似关系：

将TSCW函数与Hanning函数、Nuttall函数等窗函数作比较，可以发现其具有更加可靠的旁瓣衰减速度、旁瓣电平峰值以及主瓣宽度。

2.2.2 频域电能计量方法

根据Budeanu的研究，当电力系统中有谐波时，可按照如下两个步骤计算频域电能：

1）瞬时功率计算。按照下式计算第k次瞬时谐波有功功率pk、无功功率qk：

2）平均功率计算。按照下式计算第k次谐波平均有功功率Pk、平均无功功率Qk：

2.3 仿真分析

2.3.1 参数设置

在仿真分析过程中，须将谐波发生次数假设为2次或2次以上。此时，须按下式计算谐波情形下的电压信号：

同时，须按下式计算谐波情形下的电流信号：

仿真时，将信号采样频率fs、信号基波频率fo分别设置为1 505 Hz、50.3 Hz。同时，其它谐波、基波参数如表4所示。

2.3.2 谐波计量误差比较

基于表4的参数，本研究分别对Hanning、4-order TSCW、Black-harris和Nuttall窗作仿真分析，各窗函数谐波计量误差如图3、图4所示。

由图3可知，4类窗函数中，各个谐波频率下谐波幅值相对误差最大的是Black-harris窗函数，其次是Nuttall窗函数。当谐波频率低于6.0时，Hanning窗函数谐波幅值相对误差略大于4-order TSCW窗函数；当谐波频率高于6.0时，Hanning窗函数与4-order TSCW窗函数的谐波幅值相对误差基本一致。

类似地，由图4可知，在全部谐波频率下，4-order TSCW窗函数谐波相角相对误差也十分理想。可见，4-order TSCW窗函数的谐波计量可靠性最高。

表4 电压与电流信号的基波和谐波参数

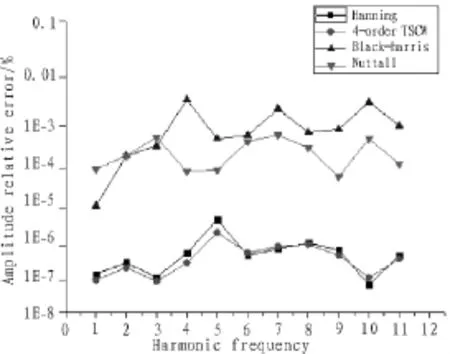
图3 各谐波幅值相对误差

图4 各谐波相角相对误差

2.3.3 有功功率计量误差比较

本次仿真中，不同窗函数在相同谐波条件下的电能计量精度存在显著差异。如表5所示，4-order TSCW窗函数有功功率计量误差不仅大幅度低于Nuttall窗函数、Black-Harris窗函数，而且也显著低于Hanning窗函数。可见，在本次仿真所选择的4种经典窗函数中，TSCW不仅可以精准进行谐波计量，而且可以将电能计量结果精度控制在最理想水准。

表5 有功功率仿真计量相对误差统计

3 结 论

在电网智能化建设过程中，实现电能采样和计量工作智能化是必然趋势。然而，电网谐波的存在不仅可能影响电能计量结果精准度，而且还可能造成电能浪费并影响电力设备性能评估精确性。基于用户终端，本研究拟对谐波进行傅立叶变换分析、SREFT分析；进一步地，就如何改进谐波计量进行算法讨论和仿真分析。经过分析和讨论，得出如下5点基本结论：

1）各类常见谐波分析算法中，分裂基FFT算法（即SREFT算法）运算次数、运算时间最少；

2）SREFT算法不仅具有运算量少的优点，而且其计算过程简单、内部数据结构清晰，便于进行二进制编程。

3）综合无精度参照物、旁瓣衰减速率、精确信号分析等方面的标准，Hanning窗函数具有相对理想的电能计量性能。

4）将三角自卷积窗TSCW函数与Hanning函数、Nuttall函数等窗函数作比较，发现其具有更加可靠的旁瓣衰减速度、旁瓣电平峰值以及主瓣宽度。

5）在全部谐波频率下，4-order TSCW窗函数谐波幅值相对误差、谐波相角相对误差都相对较理想，其谐波计量可靠性最高。同时，在本仿真所选择的4种经典窗函数中，TSCW不仅可以精准计量谐波，而且可以将电能计量结果精度控制在最理想水准。

[1]李景魁.基于AT89S52单片机的多路电能数据采集系统的设计[J].制造业自动化，2011，33（9）:80-81.

[2]陈琼，李秀平，杨杰，等.一种基于ATmage64的无线电能数据采集系统的设计 [J].电子器件，2014（5）:1004-1008.

[3]李晓蕾，吴凯.电能表数据采集器研发及应用[J].自动化与仪器仪表，2013（3）:133.

[4]尹项根，李振兴，刘颖彤，等.广域继电保护及其故障元件判别问题的探讨[J].电力系统保护与控制，2012，40（5）:1-9.

[5]Gao Guang-ling,Pan Zhen-cun,Gao Hou-lei,et al. Study on electrical digital simulation systemfollowing IEC61850[C]//Asia-Pacific Power and Energy Engineering Conference,2009:20-25.

[6]李美花，闫卫平，王颖，等.微传感器阵列多通道数据采集和处理系统 [J].电子测量与仪器学报，2016（2）：311-317.

[7]齐超，周志宇.调控中心监控自动化系统与通讯功能浅析[J].电子设计工程，2012，20（23）:127-130，133.

[8]苗彧智，王艳.基于单片机的智能电表设计[J].现代电子技术，2015（2）:59-61.

[9]王亚东，高岩，金锋.智能电表数据分析及应用综述研究[J].信息技术，2015（2）:64-68.

[10]程瑛颖，肖冀，周峰，等.智能电表数据采集新型网络结构与传输协议[J].自动化与仪表，2015（7）:9-12.

[11]黄亮，王景存，康之讷，等.新型电能计量芯片RN8302在智能电表中的应用[J].电子设计工程，2013，21（3）:93-95.

[12]康雪娟，薛荣辉.基于HT46F49E的低成本智能电表设计[J].电子设计工程，2013，21（14）:144-146.

[13]郑春芳，张波，丘东元.基于沃尔什函数的逆变器选择性谐波消除技术开关角的快速求解[J].中国电机工程学报，2005，25（22）:38-44.

[14]王冠军.基于 MSP430低功耗自动抄表系统的设计[D].吉林:吉林大学，2008.

[15]Herrera R S,Salmeron P,Hyosung K.Instantaneous reactive power theory applied to active power filter compensation:differentapproaches,assessment,and experimentalresults [J].IEEE Transactions on Industrial Electronics，2008，55（1）:184-195.

Harmonic analysis and measurement improvement method for electric energy data acquisition user terminal

WU Shao-cheng1，WANG Zheng2
（1.Shenzhen Power Supply Bureau Co.，Ltd，Shenzhen 518000，China；2.Yantai Dongfang Wisdom Electric Co.，Ltd，Yantai 264000，China）

The smart meter is the electric energy data acquisition terminal users which are currently the most promising.In order to improve power grid harmonic pollution and power quality，fast Fourier transform（FFT）was used to calculate the harmonic analysis of operation efficiency.And then complex sequence division based harmonic analysis method was proposed，which improve the operation efficiency of harmonic analysis.The improvement method of electric energy measurement based on triangular selfconvolution window is proposed，and the simulation results are compared.The research shows that the measurement accuracy of active power was significantly higher than that of typical window function based on the power measurement method of triangular self-convolution window.The measurement accuracy of the triangular self-convolution window is 1～2 orders of magnitude higher than that of Nuttall window.

smartmeter；harmonic analysis；measurement method improvement；triangular selfconvolution window；complex sequence splitting

TN86

：A

：1674－6236（2017）03-0104-05

2016-04-29稿件编号：201604277

国家863智能电网重大专项课题（2011AA05A111）

伍少成（1972—），男，湖南衡阳人，博士研究生，高级工程师。研究方向：电能智能计量、自动化技术应用。