柔性挡土结构土压力与位移关系分析

靳雪梅，李锁柱

（1.山西工程技术学院，山西 阳泉 045000；2.中交第一航务工程局有限公司，天津 300461）

柔性挡土结构土压力与位移关系分析

靳雪梅1，李锁柱2

（1.山西工程技术学院，山西 阳泉 045000；2.中交第一航务工程局有限公司，天津 300461）

为了进一步研究土压力随柔性挡土结构位移的变化规律和柔性挡土结构的土压力与位移之间的关系，根据作用在柔性挡土结构的土压力和位移的工程实测数据，通过对土压力随位移变化规律的分析，发现墙体位移类型从绕墙底转动逐渐变为向墙中部凸起的抛物线形的整个过程当中，土压力沿深度始终呈线性分布。另外，根据各工况下柔性挡土结构的实测位移，采用正弦模型和双曲线模型分别计算出土压力值，发现二者计算结果十分相近，并且与实测土压力较为接近。因此，正弦模型和双曲线模型能较好地对本工程的土压力与位移关系进行拟合。

土压力；位移；实测；柔性挡土结构

0 引言

土压力的研究是一个古老的课题。时至今日，依然有许多学者在研究这个课题。这是因为一方面经典的Rankine和Coulombg土压力理论都假定土压力是线性分布的，而众多试验表明，土压力受墙体变位方式的影响，并非总是呈线性分布；另一方面经典的土压力理论是建立在土体处于极限状态下的土压力理论，并未考虑位移大小对土压力的影响；另外，经典土压力理论和许多试验研究都是以刚性挡土结构为研究对象的，这些成果是否同样适用于柔性挡土结构，还需实践进一步检验。

1 研究现状

1.1 在不同位移类型下的土压力分布情况试验研究现状

影响土压力分布及大小的因素很多，不过一般都认为与墙的3种位移类型有关（即墙体平移、绕墙顶转动和绕墙底转动）。

Terzaghi[1]对刚性挡土墙6种不同位移方式下的主动土压力分布进行了定性研究，指出当挡土墙平移和绕墙顶转动时，主动土压力为非线性分布；当挡土墙绕墙底转动时，主动土压力分布与库仑土压力理论假设相似，为直线形分布。而Y.S.Fang[2]的试验证实，墙在3种位移时土压力分布形状及大小都不同，而平移时则为底部压力不为零的抛物线分布。另外，国内学者周应英、任美龙[3]、岳祖润[4]和徐日庆等[5]也对土压力问题进行了很有意义的试验研究。

1.2 考虑位移的土压力计算理论研究现状

在计算理论方面，陈国兴[6]等提出了考虑受位移影响的土压力折减系数法；徐日庆[7]、张吾渝[8]建立了考虑位移和时间效应的土压力计算公式；卢坤林等[9-14]提出了考虑位移影响的土压力近似计算方法。纵观这些计算公式，有些仅为纯理论推导，有些也只是针对个别试验或实测数据进行了验证，对于相同条件下的工程问题，各家的计算结果也有一定差距。因此，公式的适用性还需大量的工程数据进一步验证。

本文拟根据天津港南疆港区神华煤炭码头建设工程2座廊道的实测数据，对土压力的分布情况和土压力与位移关系进行进一步的分析和研究。

2 公式的选取

关于考虑位移的计算模型有正弦模型、指数模型、双曲线模型、Mindlin解计算模型等，作者在分析各家计算模型时发现，张吾渝[8]用正弦模型建立的考虑位移的主动土压力计算公式（式（1））和卢坤林[13]用双曲线函数建立的考虑位移影响的主动土压力近似计算方法（式（2）），虽然二者的曲线模型和计算公式不同，但在相同情况下，计算出的土压力却非常接近。下面，通过以下算例对两式的计算结果进行对比。

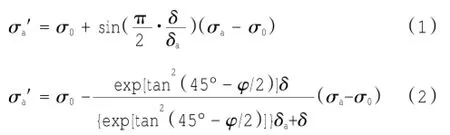
式中：σ0为土体水平应力，即静止土压力，kPa；σa为土体达到主动极限平衡状态时的土压力，kPa；σa′为挡土结构达到某一位移时的主动土压力，kPa；δa为土体达到主动极限平衡状态时的位移，mm；δ为土体的位移，mm。

取挡土结构高H=10 m，墙后填土重度γ= 18.6 kN/m3，内摩擦角φ=20°，有效内摩擦角取φ′=φ+2°，黏聚力C=10 kPa，取δa=0.004H= 40 mm，K0=1-sinφ′，σa按朗肯公式计算。假定不同的土体位移δ，分别按式（1）和式（2）计算深度为5 m处的土压力，结果如表1。在其它条件不变的情况下，令土体位移δ=20 mm，假定不同的内摩擦角φ，计算深度为5 m处的土压力，如表2。

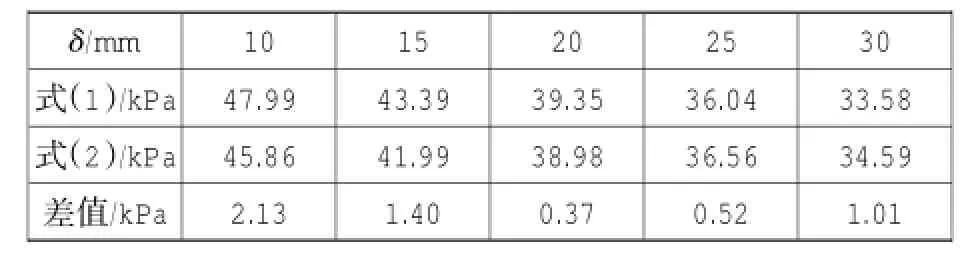
表1 两式在不同位移情况下土压力计算值对比Table 1 Calculated value contrast of earth pressure by 2 formulas under different displacements

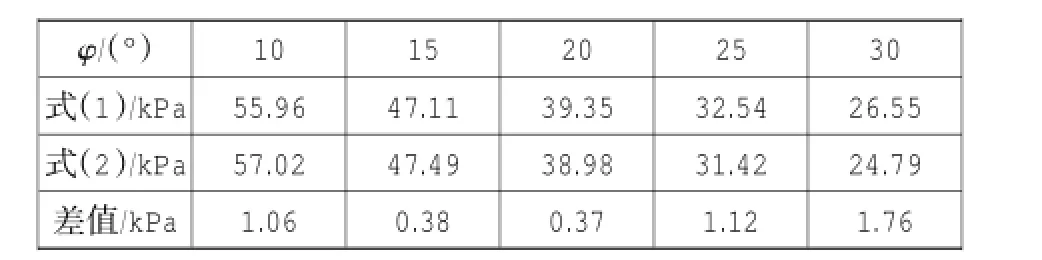
表2 两式在不同内摩擦角情况下土压力计算值对比Table 2 Calculated value contrast of earth pressure by 2 formulas under different internalfriction angles

从表1和表2的计算结果可以看出，随着计算参数δ和φ的改变，式（1）和式（2）的计算结果始终相近，误差不超过5%。

式（1）和式（2）的计算公式均较为简单，计算参数不需复杂的反演确定。如果两式经过验证能合理模拟土压力与位移关系，则非常适合在工程中推广使用。

另外，由文献[8]、[13]可知，式（1）的合理性并未进行实测土压力与位移关系的工程验证，式（2）的合理性也仅通过杨斌[9]的室内试验数据和陈页开[15]的数值模型进行了验证。因此，有必要通过工程实例对上述两式的适用性进行进一步的验证。

3 工程实例

3.1 工程概况

本文采用天津港南疆港区神华煤炭码头建设工程2座廊道的实测数据进行分析。廊道的一端与圆形结构的翻车机房相连，廊道基坑支护结构为带有内撑的2道平行地下连续墙，内撑将二道平行的地下连续墙联结成一个整体，共同承担外部压力。廊道结构外形为直线形，由54片地下连续墙组成，墙厚0.8 m，顶标高设为±0.0 m。

每道地下连续墙设置2个观测断面，观测断面分别设置在第7、13片地下连续墙上， 2座廊道基坑4道地下连续墙共计8个观测断面。本文选取2-A2和1-B2两个断面进行分析，其中2-A2断面的墙底标高为-29.0 m；1-B2断面的墙底标高为-26.0 m。

每个观测断面沿地下连续墙外侧埋设7个土压力传感器为1组，2座廊道共8组。土压力仪器编号从上至下依次为T-1～T-7，安装标高从-3.0～-21.0 m，每隔3 m安装1个，其具体埋设标高如表3。

表3 仪器埋设标高一览表Table 3 Table for the embedding evolution of the instrument

廊道基坑设第一、二道混凝土内撑和第三道钢内顶撑（具体标高如图1）。基坑分4次开挖，边开挖边支护。根据开挖深度和支撑情况的不同，可分为4个工况。一（二）号廊道岩土层主要物理力学性质指标如表4。

3.2 实测各断面在不同工况下的位移变化图

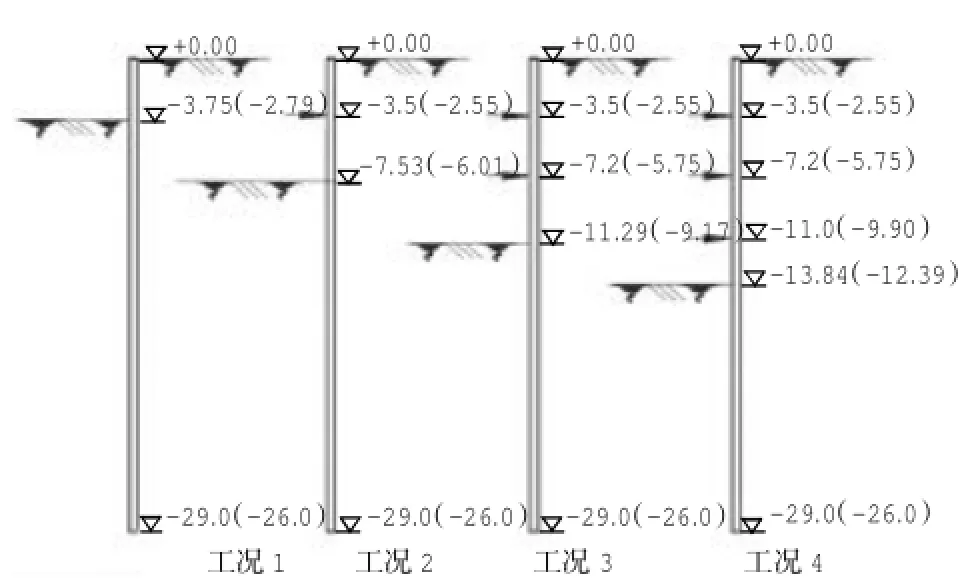
图1 廊道A（B）断面开挖工况图Fig.1 Corridor A(B)section excavation working condition diagram

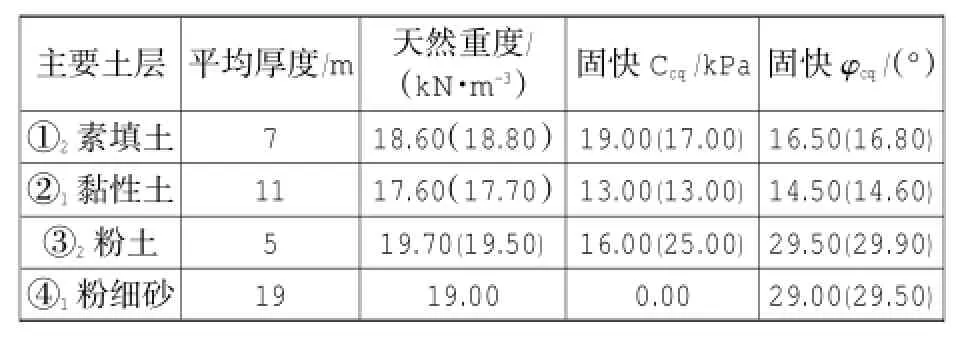
表4 一（二）号廊道岩土层主要物理力学性质指标Table 4 The main physicalmechanicalproperties indicators of1st(2nd)corridor geotechnical layers

各断面在不同工况下的位移变化曲线如图2所示。图中指向基坑内部的位移为正，反之为负。曲线编号为深层位移曲线的测量日期，如7-4指的是7月4日测量的变形曲线。图2中所示每个断面有6个观测日期的位移曲线，前4个观测日期从前到后分别为开挖第1～4层土后（即工况1～工况4）第2日的连续墙位移曲线。第5个观测日期为在A（B）断面-13.64 m（-12.19 m）标高处浇筑混凝土底板后的位移曲线。第6个观测日期是在两道连续墙内回填土方后的观测位移曲线。由于影响因素复杂，本文未对第5、6两个观测日期的位移曲线进行分析。

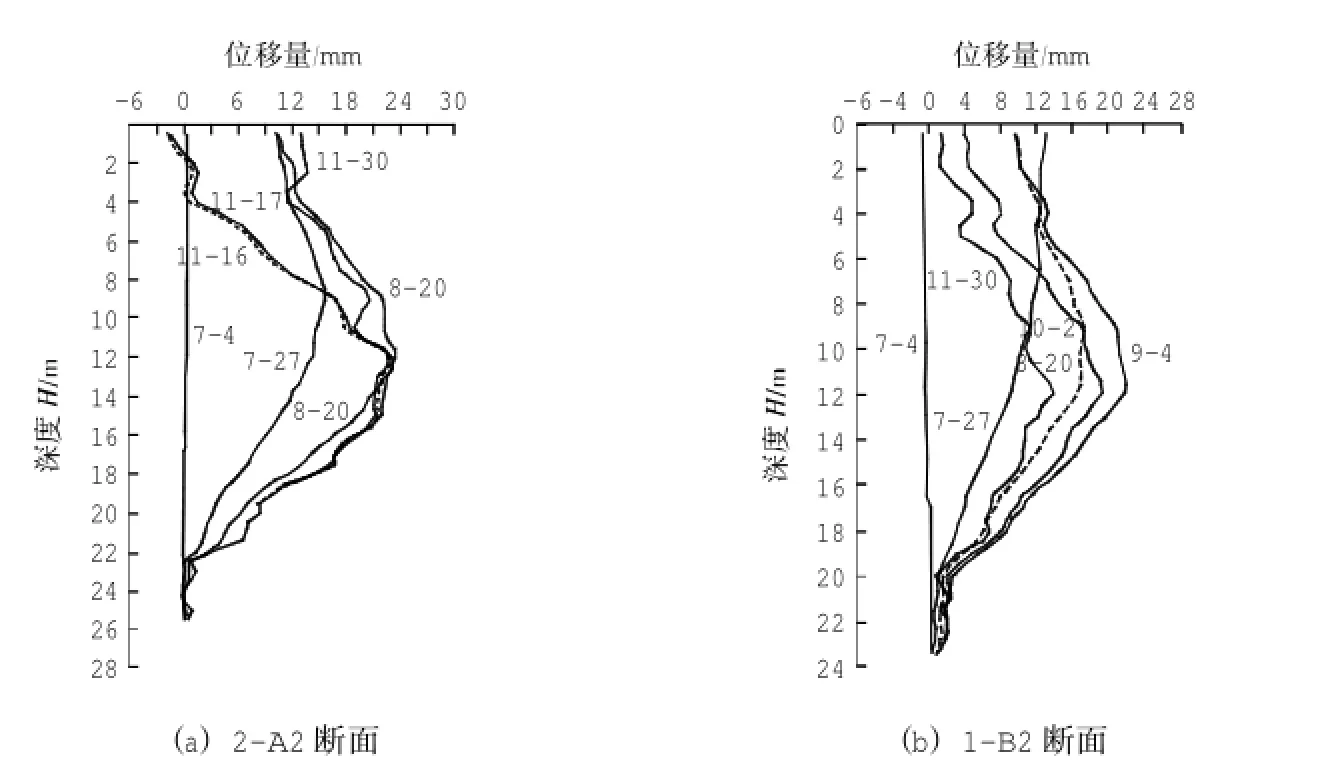
图2 深层侧向位移与深度关系曲线Fig.2 Relation curve between deep lateraldisplacement and depth

从图2可以看出，开挖初期由于开挖深度较浅，墙体以墙底为中心整体倾斜，墙体的最大挠度出现在墙顶，此时的位移曲线仍呈现直线状；随着开挖深度的增加，墙体内外侧的压力差，以及顶撑应力使墙体的最大弯矩所在标高下移，引起墙体的最大挠度所在标高也下移，测斜曲线在此处凸出，位移曲线呈抛物线状，在基坑开挖到

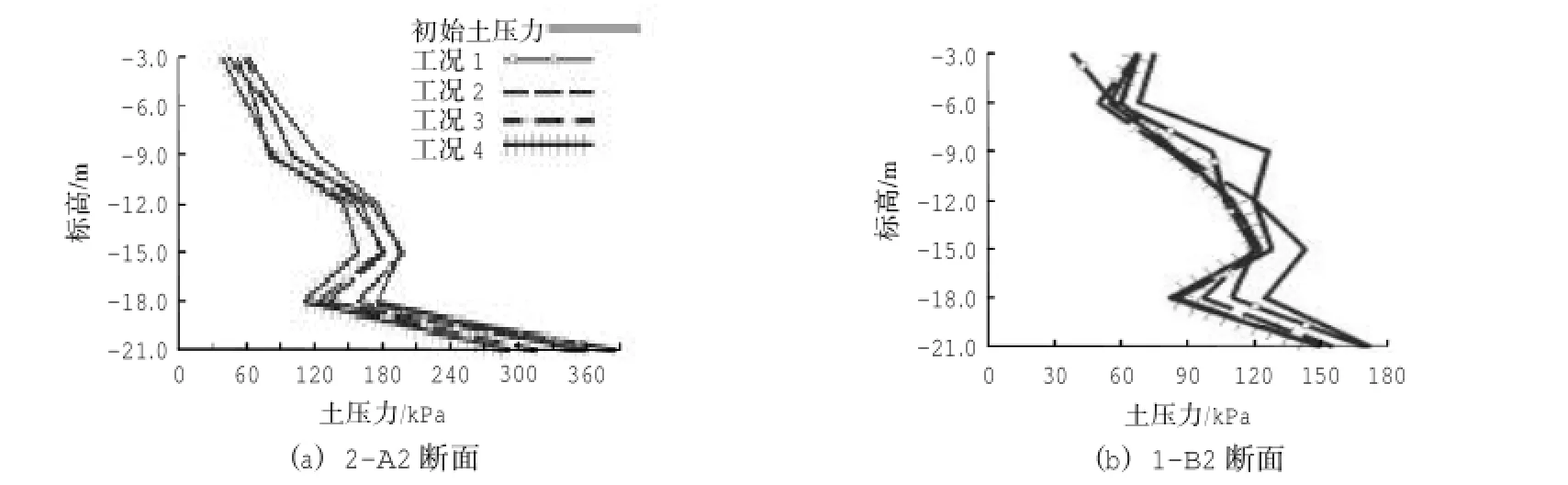
图3 不同工况下各断面土压力分布图Fig.3 Earth pressure distribution curve of every section under differentworking conditions

结合土层分布情况可发现，土压力减小位置大体在③2粉土层，对比③2粉土与②1黏性土的抗剪强度指标可知，③2粉土的抗剪强度指标远大于②1黏性土，由此可推断-18.0 m土压力减小是由于土层抗剪强度指标增大的原因。因此，可认为在各工况下土压力沿深度在墙后呈线性分布。

由图2可知，墙体位移类型在开挖初期为绕墙底转动，随着开挖深度的增加逐渐变为向墙中设计标高后，墙体最大挠度出现在基坑底面附近，深度在11～13 m。

3.3 实测各工况土压力分布图

在各工况下的土压力分布图如图3所示。从图中可以看出，在各工况下的土压力从墙顶开始随深度的增加而逐渐增大，在-18.0 m标高处略有减小后，随深度的增加继续增大。部凸起的抛物线形。但整个过程当中，土压力的分布情况沿深度始终为线性分布，说明土压力的分布情况未受位移类型变化的影响。

3.4 计算公式验证

根据图2所示，由2-A2和1-B2断面在各工况下的位移采用式（1）和式（2）计算出相应的土压力（式中σ0取开挖前实测初始土压力，σa按朗肯土压力计算），并与实测的土压力进行比较（见图4）。

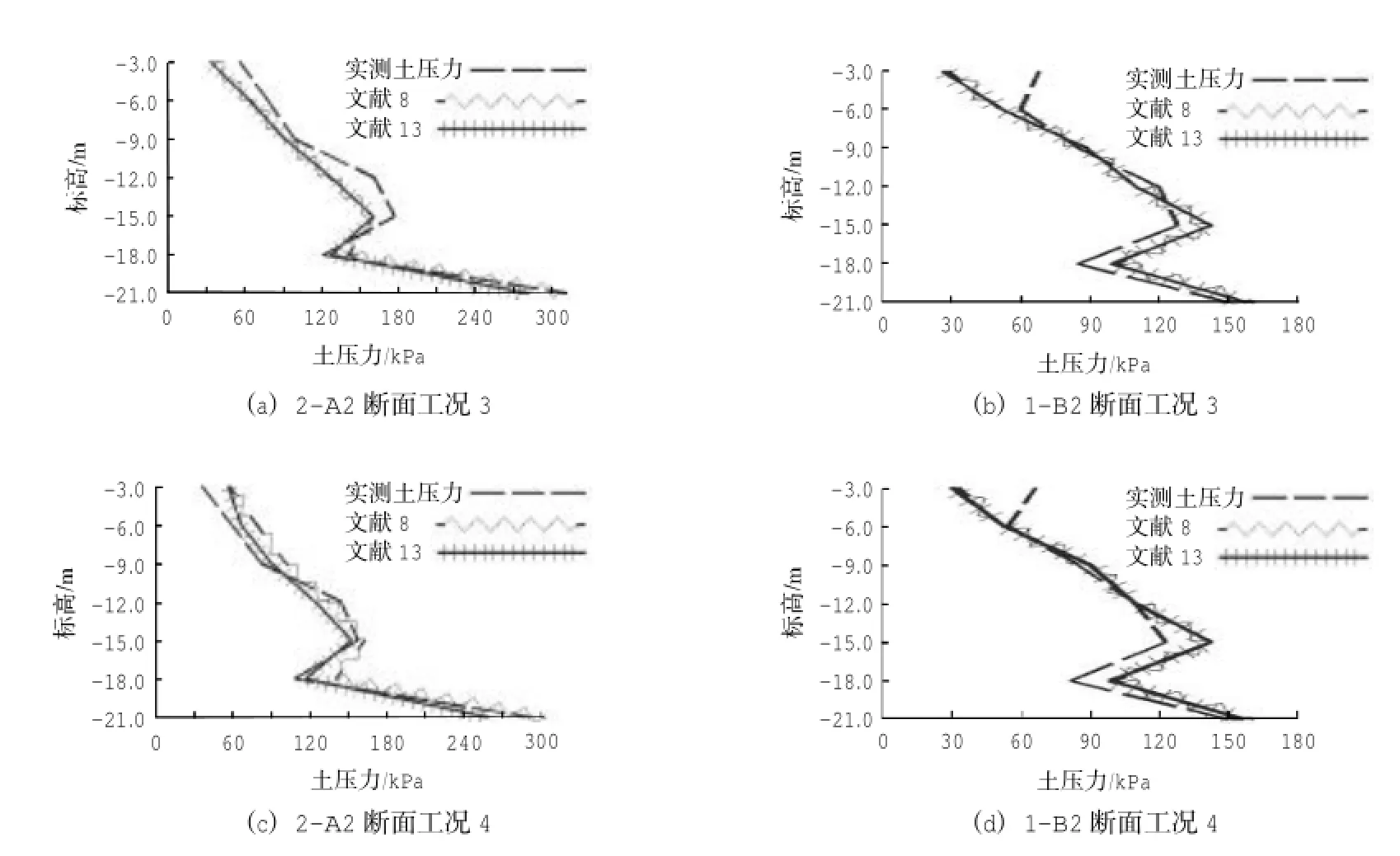
图4 土压力-深度曲线Fig.4 The curve ofsoilpressure and depth

从图4可以看出，式（1）与式（2）的计算结果相近，与前述模型计算结果一致，并且与实测土压力曲线能较好地拟合。因此，式（1）和式（2）的合理性得到了很好的验证。

4 结语

本文通过对天津港南疆港区神华煤炭码头建设工程2座廊道的土压力和位移实测数据的分析，可以看出：

1）墙体位移类型从绕墙底转动逐渐变为向墙中部凸起的抛物线形的过程中，土压力的分布情况未受位移类型变化的影响，沿深度始终为线性分布。

2）土压力和位移关系的实测曲线，能与式（1）正弦模型和式（2）双曲线模型的计算曲线较好的拟合。

当然，挡土结构土压力的计算是个相当复杂的问题，影响因素众多。本文的分析结果是否适用，还需要大量工程数据进行验证。希望本文能对土压力与位移问题的进一步研究起到一定的借鉴和参考作用。

[1]TERZAGHI K.Record earth pressure testing mechine[J].Engineering News Record,1932,109:365-369.

[2] FANG Y S,ISHIBASHII.Static earth pressures with various wall movements[J].Journalof Geotechnical Engineering,1994,120(8): 317-333.

[3] 周应英，任美龙.刚性挡土墙主动土压力的试验研究[J].岩土工程学报，1990，12（2）：19-26. ZHOU Ying-ying,REN Mei-long.An experiment study on active earth pressure behind rigid retaining wall[J].Chinese Journal of Geotechnical Engineering,1990,12(2):19-26.

[4]岳祖润，彭胤宗，张师德.压实黏性填土挡土墙土压力离心模型试验[J].岩土工程学报，1992，14（2）：90-95. YUE Zu-run,PENG Yin-zong,ZHANG Shi-de.Centrifugalmodel test of soil pressure of compacted cohesive soil retaining wall[J]. Chinese Journalof GeotechnicalEngineering,1992,14(2):90-95.

[5]徐日庆，陈页开，杨仲轩，等.刚性挡土墙被动土压力模型试验研究[J].岩土工程学报，2002.24（5）：569-575. XU Ri-qing,CHEN Ye-kai,YANG Zhong-xuan,et al.Experimentalresearch on the passive earth pressure acting on a rigid wall [J].Chinese Journal of Geotechnical Engineering,2002,24(5): 569-575.

[6] 陈国兴，韩爱民.关于基坑支护结构土压力计算的若干意见[J].工程兵工程学院学报，1999，14（1）：33-37. CHEN Guo-xing,HAN Ai-min.Some opinion on the earth pressure computing ofthe fender structures on the excavation engineering[J].Journal of Nanjing Engineering Institute,1999,14(1):33-37.

[7] 徐日庆.考虑位移和时间的土压力计算方法[J].浙江大学学报：工学版，2000，34（4）：370-375. XU Ri-qing.Methods of earth pressure calculation for excavation [J].Journal of Zhejiang University:Engineering Science,2000,34 (4):370-375.

[8] 张吾渝，徐日庆，龚晓南.土压力的位移和时间效应[J].建筑结构，2000，30（11）：58-61. ZHANG Wu-yu,XU Ri-qing,GONG Xiao-nan.Displacementand time effectof earth pressure[J].Building Structure,2000,30(11): 58-61.

[9]杨斌，胡立强.挡土结构侧土压力与水平位移关系的试验研究[J].建筑科学，2000，16（2）：14-20. YANGBin,HULi-qiang.Teststudy on relationship between lateral earth pressure on retaining structures and horizontal displacement [J].Building Science,2000,16(2):14-20.

[10]宰金珉，梅国雄.考虑位移的土压力模型研究[J].南京建筑工程学院学报，2001（1）：9-20. ZAIJin-min,MEIGuo-xiong.Rankine earth pressure modelconsidering deformation[J].Chinese Journal of Rock Mechanics and Engineering,2001(1):9-20.

[11]卢国胜.考虑位移的土压力计算方法[J].岩土力学，2004，25（4）：586-589. LU Guo-sheng.A calculation method ofearth pressure considering displacement[J].Rock and SoilMechanics，2004,25(4):586-589.

[12]张文慧，田军，王保田，等.基坑围护结构上的土压力与土体位移关系分析[J].河海大学学报：自然科学版，2005，33（5）：575-579. ZHANG Wen-hui，TIAN Jun,WANG Bao-tian,etal.Relationship between earth pressure on support structure of foundation pits and displacementof earth mass[J].Journalof Hohai University:Natural Sciences,2005,33(5):575-579.

[13]卢坤林，杨扬.考虑位移影响的主动土压力近似计算方法[J].岩土力学，2009，30（2）：553-557. LU Kun-lin,YANG Yang.Approximate calculation method of active earth pressure considering diaplacement[J].Rock and Soil Mechanics,2009,30(2):553-557.

[14]魏焕卫，杨敏，贾强，等.基于Mindlin解的土压力位移计算模型[J].岩土力学，2011，32（2）：495-502. WEIHuan-wei,YANG Min,JIA Qiang,etal.Calculation modelof soilpressure displacementbased on Mindlin solution[J].Rock and SoilMechanics,2011,32(2):495-502.

[15]陈页开，汪益敏，徐日庆，等.刚性挡土墙主动土压力数值分析[J].岩石力学与工程学报，2004，23（6）：989-995. CHEN Ye-kai,WANG Yi-min,XU Ri-qing,et al.Numerical analyses ofactive earth pressure on rigid retaining wall[J].Chinese JournalofRock Mechanics and Engineering,2004,23(6):989-995.

Relations analysis on earth pressure and displacement of flexible retaining structure

JIN Xue-mei1,LISuo-zhu2
（1.ShanxiInstitute of Technology,Yangquan,Shanxi045000,China; 2.CCCC First Harbor Engineering Company Ltd.,Tianjin 300461,China）

In order to further study on earth pressure variation with flexible retaining structure displacement and the relationship between earth pressure and displacement on the flexible retaining structure,according to the measured data of the earth pressure and the displacement on the flexible retaining structure,through the analysis of variation of earth pressure with displacementofthe structure,we found that the wall displacement type has gradually changed from around the structure at the end of the rotation to a parabola shaped structure raised in the middle,the earth pressure along the depth is linear distribution in the whole process.In addition,according to the measured displacements offlexible retaining structure under various working conditions,we respectively calculated the earth pressure value by sine model and hyperbolic model,found that the two results are very similar,and are close to the measured earth pressure.Therefore,the two models can be used to fit the relationship between pressure and displacementof the project.

earth pressure;displacement;actual measurement;flexible retaining structure

U655.54；TU432

A

2095-7874（2017）02-0028-05

10.7640/zggwjs201702006

2016-08-30

2016-11-17

靳雪梅（1975— ），女，山西阳泉人，硕士，副教授，主要从事岩土工程方面的研究与教学工作。E-mail：jxm19750520@163.com