基于PFC-COMSOL的砂井地基固结过程数值模拟分析

侯宏伟，戴先平，徐霞

（1.浙江省建筑科学设计研究院有限公司，浙江 杭州 310012；2.浙江省吉安县城西北开发有限公司，浙江 安吉 313399）

基于PFC-COMSOL的砂井地基固结过程数值模拟分析

侯宏伟1，戴先平2，徐霞2

（1.浙江省建筑科学设计研究院有限公司，浙江 杭州 310012；2.浙江省吉安县城西北开发有限公司，浙江 安吉 313399）

采用PFC-COMSOL联合的方法进行了砂井地基固结过程的数值模拟，建立了砂井地基细观模型和渗流场模型，从而对固结过程中，土颗粒的压缩及排列、土体各深度处孔隙率及渗透系数的变化进行了分析。得出结论：采用PFC-COMSOL联合求解方案模拟砂井地基固结，可较直观地得到不同时刻地基的沉降量以及内部渗流场分布情况；随着固结时间的推移，土体颗粒排列均匀且紧密；在地基固结过程中，不同深度土层处的孔隙率及渗透系数均随固结时间呈减小的趋势。

PFC-COMSOL联合方案；细观分析；数值模拟；孔隙率变化

0 引言

在我国沿海沿江地区的工程建设过程中常面临大面积的软土地基，由于此类软土地基的渗透性较差，其固结时间较长，实际工程中通常采用排水固结法处理软土地基，通过在软土地基中添加砂井或塑料排水板达到加快地基固结排水速度的目的。

目前众多学者对软土排水固结沉降特性进行了大量的研究。从Terzaghi[1]提出一维固结理论以来，研究者根据实际情况提出了新的固结理论，如Hansbo[2]、谢康和[3]等提出的软土固结理论，使整个宏观固结理论体系不断完善。同时，对于竖井地基固结的数值模拟研究，常采用有限元法、边界元法等进行分析[4]，传统的固结理论及数值模拟大部分是从宏观角度分析土体固结问题，而对软土体细观层面的变化特征研究较少。对于土体细观结构的研究，王宝军[5]等将GIS数据提取技术与图像处理技术结合，通过对土体细观结构图像进行分析，实现了利用分形定理研究土体细观结构定量方法；对于软土微观结构的数值分析方面，高彦斌[6]等根据黏粒的微观形态特征，利用PFC-2D软件建立黏性土的微观模型，分析了微观结构对其力学性质的影响；陈蕾[7]等采用PFC-2D软件从微观方面出发，利用颗粒流中的clump单元来模拟黏性土无侧限抗压试验的基本颗粒和“柔性边界”，具有良好的模拟效果。但在软土地基砂井排水固结过程的数值模拟分析中，对软土体内的细观结构研究较少。

本文为对软土地基砂井固结进行细观分析，将以某沿海公路工程为依托，采用颗粒流软件PFC建立逼近真实软土结构特征的细观模型，以分析在固结压缩过程中土体颗粒的重新排列情况，从细观上分析土体的固结压缩特性；同时针对PFC软件关于砂井地基渗流场分析方面的不足，引入了COMSOL软件进行渗流场模型的计算分析，并编写数据转换平台，实现 PFC模型与COMSOL模型的信息交互运算，联合求解砂井地基固结问题；同时通过PFC-COMSOL的联合模拟结果，对比分析地基土体的压缩沉降及孔隙率等的变化规律。

1 PFC-COMSOL联合求解方案的实现

1.1 PFC既有渗流分析方案

软土固结是水从土体内部排出的过程，因此对土体的排水固结的数值模拟分析需要考虑渗流场的模拟方法。PFC用于细观地分析软土固结过程，本身具有了流场计算功能[8]。其自带的两种流场计算方案分别为管-域网格模型和粗糙网格模型，如图1。

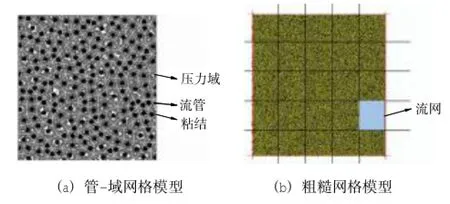
图1 流场分析方法示意图Fig.1 Sketch of flow field analysis method

对于前者，压力域的形成需要依托颗粒组成孔隙，土体孔隙率较大时，模型中颗粒极有可能不完全接触，此时，无法形成封闭的孔压域，因此，该方案用于分析孔隙率较大的软黏土固结存在一定的缺陷。对于后者适用于砂土等多孔介质的渗透系数，但并不适用于软土，因为软土存在结构性，其渗透系数计算较为复杂，因此在分析过程中，无法完成软土渗透系数的标定工作。

针对上述问题，采用COMSOL Multiphysics软件对土体内部的渗流场进行模拟。COMSOL是专为描述和模拟各种物理现象而开发的基于有限元分析的软件，利用其达西定律模块对土体内部流场进行模拟，计算过程简单方便。

1.2 PFC-COMSOL耦合原理

倪小东等[8]根据固-液两相间的相互作用条件，由土体颗粒组成的多孔介质中，首先取单位土体进行受力分析，考虑单位土体内颗粒受力平衡，求得颗粒与流体作用时，作用在单个颗粒上的力。

本文将COMSOL中当前时步的渗流场转换为每一个颗粒受到的渗流力，导入PFC细观模型中，在渗流力与荷载的共同作用下计算至稳定状态，然后将PFC中模型的尺寸信息以及孔隙率变化情况导出，在COMSOL中建立对应尺寸的新模型，将新的孔隙率信息转换为新的渗透系数导入COMSOL中，开始下一轮计算，图2为联合求解过程数据交换示意图。数据转化过程通过编写的VB程序完成，数据转换平台用户界面，可以根据需要实现PFC与COMSOL数据相互转换。

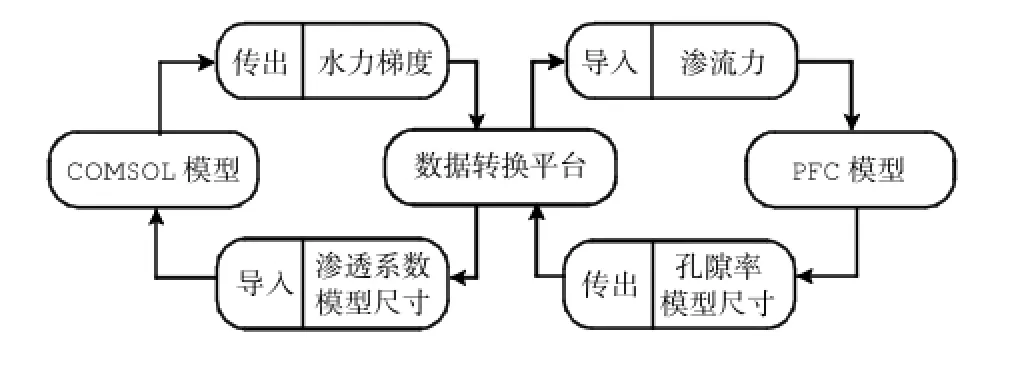
图2 PFC-COMSOL数据交换示意图Fig.2 Sketch of the PFC-COMSOL data exchange

2 砂井地基排水固结数值模拟

2.1 砂井地基细观模型

本文依托某沿海公路建设工程建立简化的饱和软土地基模型，采用堆载预压联合砂井排水固结法处理，砂井直径0.3 m，间距2 m，贯穿整个软土层，以等边三角形的方式布置，荷载为100 kPa（约6 m高填土，且假设荷载1次施加）。

为优化运算，本次模拟仅考虑单井固结条件下地基的固结情况。借鉴单井固结理论[4]假定，认为砂料及涂抹区土体只有渗透系数与未扰动土体不一样，其余性质一致；土体仅发生竖向变形且孔隙水渗流服从达西定律。

单井固结模型中，软土地基关于砂井对称，因此计算时只需要考虑一边土体的压缩情况，在等应变条件成立的前提下，可以只考虑未扰动区的压缩情况，同时适当增大未扰动区模型的宽度，以减小模型边界对计算结果的影响。

本文建立3 m×7 m的软土未扰动区细观模型（图3），使用聚粒（CLUMP）为基本单元建立模型，经过标定之后的细观参数如表1所示。

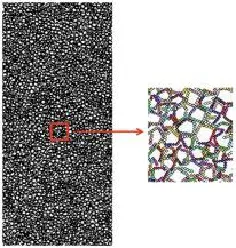
图3 均质软土地基未扰动区模型Fig.3 Softunperturbed homogeneous zone model

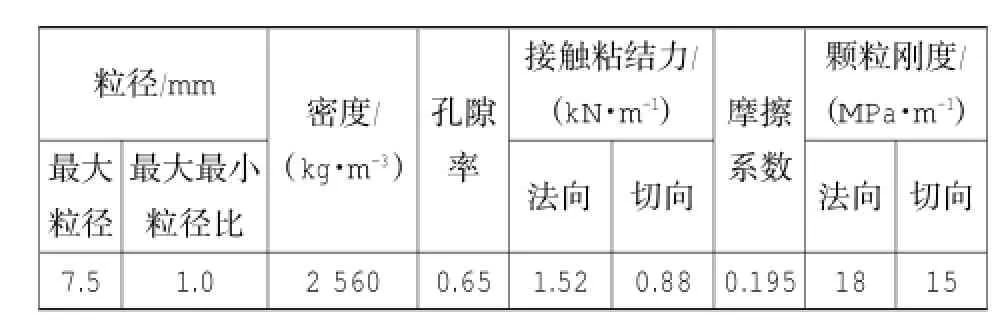
表1 PFC模型细观参数表Table 1 PFC microscopic modelparameters table

模型的初始孔隙率为0.65，考虑到天然地基在自重应力的作用下发生固结，因此本文建立均质的软土地基模型后，通过调整模型中wall的速度控制，让其在自重应力下完成固结，形成正常固结的软土地基模型，此时模型高度为6.51 m。

2.2 砂井地基渗流场模型

在COMSOL下的达西定律模块中建立软土地基单井固结的渗流场模型，图4为COMSOL模型示意图（为了标注方便，示意图尺寸与实际模型存在差异）。

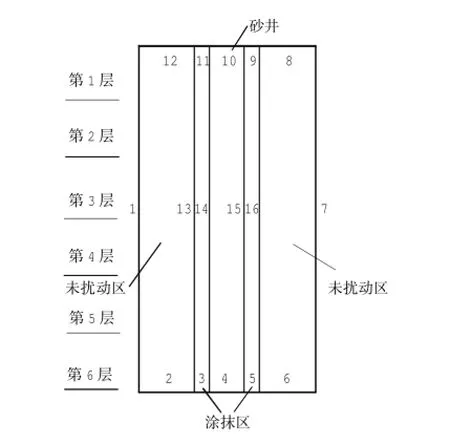
图4 COMSOL模型示意图Fig.4 Sketch of COMSOL model

模型的高度与上文建立的自重固结后的软土地基细观模型高度一致，为6.51 m。同时，对于孔隙率的监测需要分层进行，在计算过程中将模型分成等厚度的6层（图4所示），利用测量圆监测每层土样孔隙率随时间的变化情况。

在计算过程中软土地基未扰动区土体的渗透系数根据PFC模型导出的孔隙率计算得到，其中孔隙率为0.65时对应的竖向渗透系数kv为3.2× 10-9m/s。根据单井固结理论，假定砂井以及涂抹区的渗透系数不发生变化，且水平向与竖向渗透系数相同，求解域具体设置见表2。

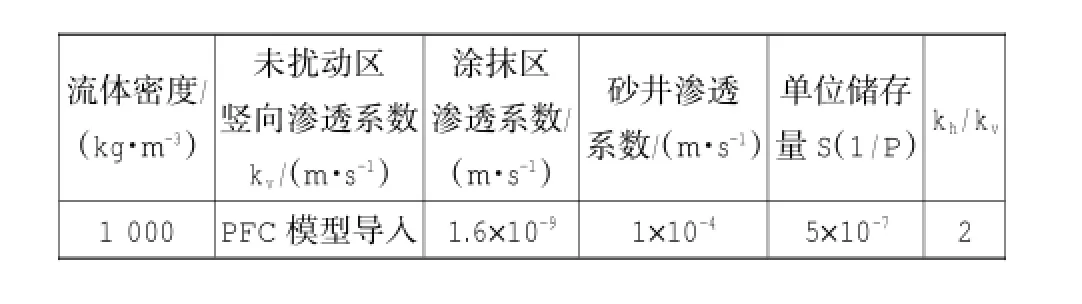
表2 求解域参数设置表Table 2 Solving domain parameter setting table

对于模型边界条件的设置主要如下：图4中边界1～7设为不透水边界；8～12设为水头边界；13～16设为连续边界。

需说明的是，由于砂井的存在，土体内部存在径向渗流和竖向渗流，因此即使两点处在同一深度也可能因为水平位置不同导致其孔压不同，借鉴经典单井固结理论引入径向平均孔隙水压力的概念，以未扰动区竖向中轴线位置处各深度的孔压（实质上是超孔压，简称孔压）作为整个软土地基未扰动区对应深度的平均孔压，并以该位置的水力梯度作为计算颗粒渗流力的依据。由于假定砂料及涂抹区土体只有渗透系数与未扰动土体不一样，其余性质一致，故将整个渗流场模型的单位储存量设为一个定值。

2.3 模型结果分析

2.3.1 土体压缩沉降及孔压分析

经多次交互运算后，完成了砂井软土地基固结过程的模拟。并选取砂井地基固结3 d和11 d的模型压缩量进行对比，其中固结3 d后PFC的压缩模型图及COMSOL的孔压云图如图5所示。

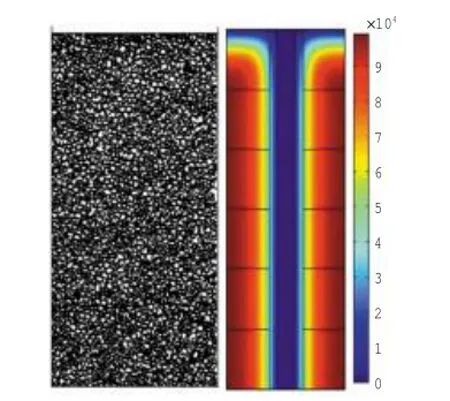
图5 2.63×105s时PFC模型压缩及COMSOL模型孔压云图Fig.5 PFC modelcompression and COMSOL modelpore pressure contours at 2.63×105s

由图5，此时模型的压缩量为0.121 m，从图中可以发现，PFC模型上层部分的颗粒分布更为密集，同时COMSOL模型上层部分孔压消散更快，表明此刻地基上部土体固结度更高，压缩量更大。

同样的方式选取固结11 d后的固结压缩模型进行分析，此时模型的压缩量为0.286 m，相比于3 d时刻，PFC模型压缩量及COMSOL模型孔压消散程度均增大，同时PFC模型依然存在上层颗粒分布更密集的现象。很好地反映出随固结时间的增长，土体持续固结压缩且土体内的孔压继续消散。为从细观上对比研究砂井地基排水过程前后，地基土体的压缩量，绘出了PFC模型的最终压缩图（图6）。

图6中，模型的最终压缩量为0.622 m。对比于初始阶段（图3），此时模型颗粒分布较为均匀，通过模型局部放大图可以发现，此时颗粒比模型初始状态时排列更紧密。

图6 PFC模型最终压缩图Fig.6 Diagram of PFC finalcompression model

整个砂井地基固结过程中沉降时程曲线如图7所示。从图中可以发现压缩速度随着时间逐渐减小，这一点与工程实际是符合的。

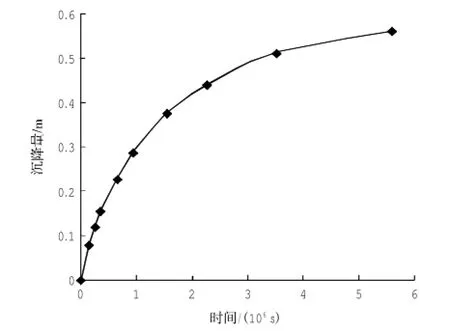
图7 沉降量随时间变化曲线Fig.7 Curve ofsettlement changing with time

2.3.2 土体孔隙率变化规律分析

在模拟砂井地基固结时，地基各层土体的孔隙率随着固结时间的推移而变化，分别绘出图4划分的各个土层的孔隙率随固结时间的曲线，如图8所示。

由图8可见，由于该模型是在自重应力下完全固结的正常固结土，因此，初始时刻（未施加荷载时）各土层的孔隙率随着深度的增加而减小，图8中土层1至土层6的初始孔隙率依次减小。从图8中可看出固结前期土层1的孔隙率减小的速度较快，土层2次之，土层3、土层4、土层5与土层6孔隙率减小的速度相对较慢，走势也较为接近，表明靠近地基顶面的土层压缩量更大，土层内部颗粒排列更密集，这一特点与图5中PFC模型压缩图以及COMSOL模型孔压分布云图反映的特点一致。

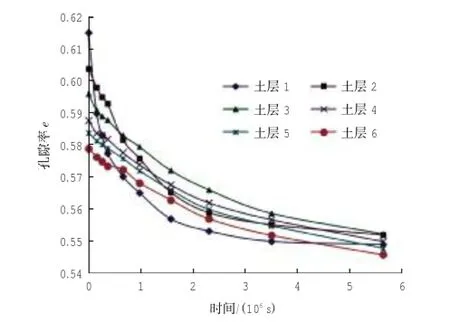
图8 模型各土层孔隙率时程变化曲线Fig.8 Each soilporosity curves by time of the model

在软土地基固结模拟过程中，模型随着固结时间的推移而产生压缩，且孔隙比减小，这都会使得地基内各深度土层的渗透性有所变化。考虑到不同土层的渗透系数是根据其孔隙比计算得到的，因此各土层竖向渗透系数随时间的变化趋势与图8中对应土层孔隙率变化曲线走势接近。

即随着软土地基固结过程的推进，各土层的渗透系数均明显减小。渗透系数决定了水排出地基的速度，直接影响了固结进程发展的快慢，因此在模拟地基固结过程时，考虑渗透系数的变化可以提升结果的准确性。

3 结语

本文利用离散元软件PFC进行颗粒的细观分析，并针对其不足，引入COMSOL进行渗流场分析，建立了PFC-COMSOL联合模拟软土砂井固结的方案。结合工程建立砂井地基细观模型及其渗流场模型，分析了PFC-COMSOL联合使用时，砂井地基固结过程中，土体的压缩沉降、孔隙率及渗透系数随时间的变化规律。得出结论主要如下：

1）建立简化的砂井软土地基模型，采用PFC-COMSOL联合求解方案模拟砂井地基固结过程，可弥补PFC软件关于渗流场分析的不足，较直观地得到不同时刻地基沉降量以及内部渗流场分布情况。

2）砂井地基的细观模型反映出，随着固结时间的推移，土体颗粒排列趋于均匀且紧密。从细观上较显著地反映出砂井地基固结压缩情况。此数值分析方法可为软土地基砂井固结的细观分析提供一个思路。

3）PFC-COMSOL联合数值分析结果表明，在地基固结过程中，不同深度土层处的孔隙率及渗透系数均随固结时间呈减小的趋势。同时，渗透系数决定了水排出地基的速度，直接影响了固结进程发展的快慢，因此在模拟地基固结过程时，考虑渗透系数的变化可以提升结果的准确性。

[1] TERZAGHI K.Erdbaumeehanik and boden physikalischer grundlage[M].Deutieke,1925.

[2] HANSBO S.Consolidation of fine-grained soils by prefabricated drains[C]//Proceedings 10th international conference on soil mechanics and foundation engineering,Stockholm,1981:667-682.

[3] 谢康和，曾国熙.等应变条件下的砂井地基固结解析理论[J].岩土工程学报，1989（2）：3-17. XIE Kang-he,ZENG Guo-xi.Consolidation theories for drain wells under equal strain condition[J].Chinese Journalof Geotechnical Engineering,1989(2):3-17.

[4]邓岳保.竖井地基固结解析理论与有限元分析[D].杭州：浙江大学，2013. DENG Yue-bao.Analytical theory and finite element analysis for consolidation ofsoftsoils by verticaldrains[D].Hangzhou:Zhejiang University,2013.

[5]王宝军，施斌，刘志彬，等.基于GIS的黏性土微观结构的分形研究[J].岩土工程学报，2004（2）：244-247. WANG Bao-jun,SHI Bin,LIU Zhi-bin,et al.Fractal study on microstructure ofclayey soilby GIS[J].Chinese Journal of GeotechnicalEngineering,2004(2):244-247.

[6]高彦斌，王江锋，叶观宝，等.黏性土各向异性特性的PFC数值模拟[J].工程地质学报，2009，17（5）：638-642. GAO Yan-bin,WANG Jiang-feng,YE Guan-bao,et al.PFC numerical simulation on anisotropic properties of cohesive soil [J].Journalof Engineering Geology,2009,17(5)：638-642.

[7]陈蕾，洪宝宁.黏性土无侧限抗压试验颗粒流软件（PFC）模拟的微观分析[J].科学技术与工程，2014，14（16）：62-66. CHEN Lei,HONG Bao-ning.PFC numericalsimulation on unconfined compressive testofcohesive soil[J].Science Technology and Engineering,2014,14(16):62-66.

[8]倪小东，赵帅龙，王媛，等.岩体水力劈裂的细观PFC-CFD联合分析[J].岩石力学与工程学报，2015（S2）：3 862-3 870. NI Xiao-dong,ZHAO Shuai-long,WANG Yuan,et al.Numerical analysis ofhydraulic fracturing ofrock mass on mesoscopic levelby coupled PFC-CFD method[J].Chinese Journal of Rock Mechanics and Engineering,2015(S2):3 862-3 870.

Numerical simulation analysis on sand drains ground consolidation process based on PFC-COMSOL

HOU Hong-wei1,DAIXian-ping2,XU Xia2
（1.Zhejiang Academy of Building Research&Design Co.,Ltd.,Hangzhou,Zhejiang 310012,China; 2.Anji County in the Northwest Development Co.,Ltd.,Anji,Zhejiang 313399,China）

We used the method of PFC-COMSOL to simulate sand drains ground consolidation process and establishing sand drain ground microscopic model and seepage field model,and analyzed the compression and the arrangement of soil and the changes ofsoilporosity and the permeability in differentdepth.The conclusions show that PFC-COMSOL simulation method of sand drains ground consolidation can obtain the settlement and the distribution of the internal seepage field of different time intuitively.Over time,the soil particles were arranged uniformly and intimately with the consolidation.The porosity and permeability coefficientatdifferentdepths in the soildecreased with consolidation time..

PFC-COMSOL joint programs；microscopic analysis;numerical simulation;porosity change

U655.54；TU471.8

A

2095-7874（2017）02-0016-05

10.7640/zggwjs201702003

2016-09-09

2016-11-21

浙江省建设科研项目（2015K31）

侯宏伟（1979— ），男，江苏滨海人，高级工程师，从事钢筋混凝土结构试验检测及研究工作。E-mail：867664687@qq.com