基于角度变化的服饰图案几何形变
高先科,徐蓼芫,徐平华,周 佳
(南通大学 纺织服装学院,江苏 南通 226019)
基于角度变化的服饰图案几何形变
高先科,徐蓼芫*,徐平华,周 佳
(南通大学 纺织服装学院,江苏 南通 226019)
从服饰图案设计的实际需求出发,利用角度变化原理和函数绘图实现图案的几何形变。确定像素点相对于图案中心点的位置,根据角度变化建立几何曲线关于中心点的方程,基于比例系数和新边界点的距离确定像素点新的坐标位置,实现多种几何形状的图案变形。该方法的实现有利于提升传统图案的设计加工效率和外观效果,满足快时尚的设计需求。
图案;角度变化;几何形变;方程
当前快时尚的消费需求对服饰图案设计提出了更高的要求,图案设计已经成为纺织品生产中的一个重要环节。造型独特、富有创意的图案往往更能吸引消费者的眼球,产品更具市场竞争力。图案的流行性和复杂性对企业设计部门提出更高的要求,图案的几何形变是图案设计与创新的重要方向之一。目前众多企业在图案几何形变的设计方面仍以人工结合绘图软件为主,导致设计效率不高、变形的形状随意性强和无法批量化操作等诸多问题。因此,需要一种高效且切实可行的方法,以提高图案形变快速、准确和高效的设计效率,弥补专业设计软件的不足。
几何形态不仅在纺织领域有着重要的运用,在室内装饰、家具设计和建筑设计行业等领域也有着广泛的运用[1-2]。图像变形算法已有很多学者做过这方面的研究。在变形的算法上,经典的算法有时永杰、黄武、杨金钟[3-5]等提出的基于网格交互、控制线段和控制点的图案变形方法;有基于多特征融合技术、路径周长比例等变形算法[6-7];还有基于轮廓线、扩展的移动最小二乘法等变形算法[8-10]。在变形运用的研究上,有医学上影像技术应用,还有视频技术、图像融合等领域的广泛运用[11-14]。上述的图像变形算法和运用,通常只是某一算法的创新和改进,并不适用于服饰图案领域的设计创造,或者图像变形比较单一,不具有通用性等。
从图案设计的实际需求出发,提出利用像素点的角度变化,建立相关方程,用以表示目标图像的边界,根据不同方程变形出图案的各种复杂、新颖的几何形状。该方法有利于提高纺织品图案设计质量和效率,满足行业快速发展的需求。
1 算法主要流程
基于像素点的角度变化以实现图案不同形状变形的算法主要流程为:
(1)确定图案中心点。一般设为原矩形图像的几何中心,坐标可通过数学计算获得,中心点是建立方程的极坐标系的极点;
(2)获取像素点位置。像素点位置指相对于(1)中的中心点(极点)而言,长度由距离公式计算得出,角度由反正切角函数atan(α)获得;
(3)建立坐标系方程。方程需要转化为极坐标系下方程,方程的函数图像即是变形的目标图像形状,极角和极径确定目标图像的边界;
(4)像素点比例系数。指认(2)中距离除以对应有相同反正切角的原图边缘像素点到中心点长度距离的值,这是像素点位置变换的主要依据;
(5)像素点坐标转换。用(4)中角度对应方程的极径长度乘以比例系数就是像素点到中心点的新距离,再转换成直角坐标,以此确定像素点新的坐标位置。
按(1)~(5)步骤完成,遍历原图中的每个像素点完成像素点位置的变换,最终实现图案的几何形态变换。
图案变形的算法流程可以用流程图简单地表示,如图1所示。
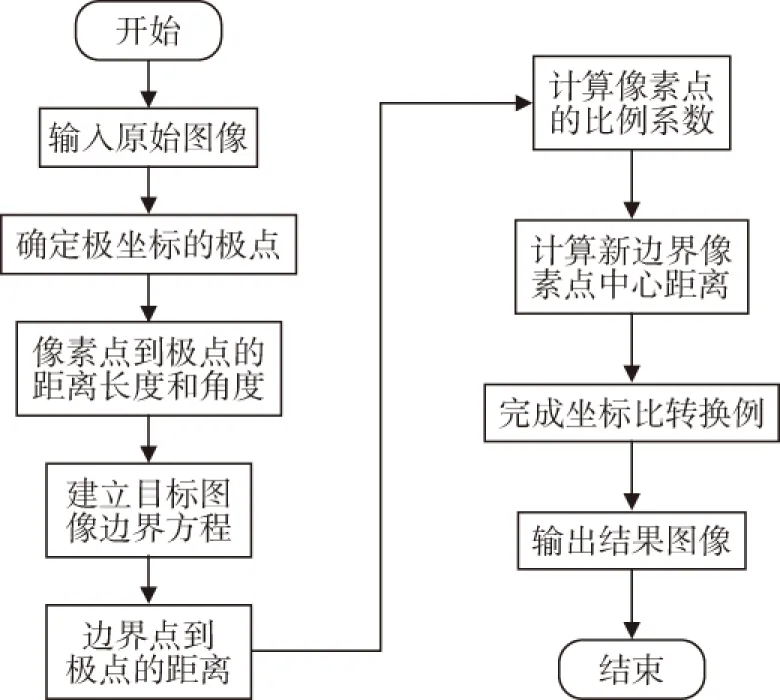
图1 算法流程示意图
2 算法主要原理
2.1 位置关系确定
任何一幅RGB彩色位图图像可以看成一个矩阵,而矩阵中的每一个元素就是位图中对应的一个像素点[15]。如图2所示,反应像素点P相对于中心点O的位置关系。P为图像中的任意一像素点,O点为图像的中心点,P点到O点的位置方向可以用α表示,本文中指四象限反正切值函数atan(α)的值,此值的范围在-π到π之间。另外,根据直角坐标系与极坐标系的位置转换关系:

(1)
根据极径OP的长,则代入(1)式求得P点相对于O点的直角坐标(x,y),即确定了P点相对于O点的具体位置。原图中任意一像素点相对与中心点的反正切值在-π到π之间,根据反正切值求得具体坐标,则相对位置都可以一一确定。

图2 像素点相对位置
2.2 图案变形原理
以目标图像是椭圆形为例,对原图进行变形,图像变形的关键是如何确定椭圆边界点的位置。如图3中,已知正方形ABCD(矩形图案变形之前需要变为正方形),极点为O点(正方形几何中心),P为任意一像素点,点O、M、P、B在同一条直线上,∠α为P点的反正切角。图像变形主要是通过改变像素点的位置实现的,即像素点坐标按一定的比例变换。图中的点P需要变换到椭圆以内OM线段上的某一点,变换的比例系数为r:
r=OP÷ON
(2)
而P点新位置坐标为(x,y):
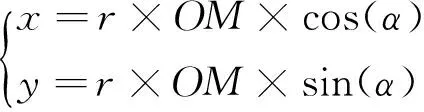
(3)
OP的距离可以用距离公式计算得出,ON和OM的长度可以看成正方形、椭圆的极坐标方程的在极角为∠α时的极径。那么ON和OM与建立方程关系:
(4)
ON的长度在α时通常固定,如上述ON的值可以通过解直角三角形OEN获得,ON=OE/cos(α)。通常原正方形图案中同一α对应的ON长度不变,图案的形变的形状有ρ1(α)确定。综上所述,极坐标方程的OM=ρ1(α)决定目标图像的形状,根据不同曲线的极坐标方程可以获得不同几何形状的变形效果。当然相关参数方程、直角坐标方程也可以转化为极坐标方程进行运用。
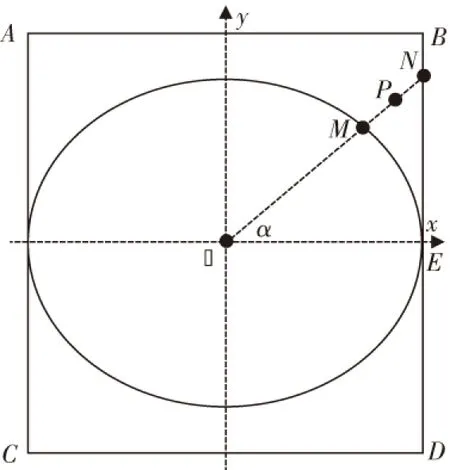
图3 图案椭圆变形原理
3 结果与分析
采用MATLAB.2014a软件对试验数据进行处理。该软件具有强大的图像处理功能,有实用性强、程序移植性高的特点。图像处理工具箱里的函数包含许多算法,可以直接使用,这样提高了编写程序的效率。试验中所用到的图案均为企业生产中的印、绣花图案。
试验结果如图4所示,对于椭圆的变形试验选取了logo图案、几何图案、花型图案和线条图案等4类不同类型的图案。极点在中心点的椭圆的极坐标方程设为:
(5)
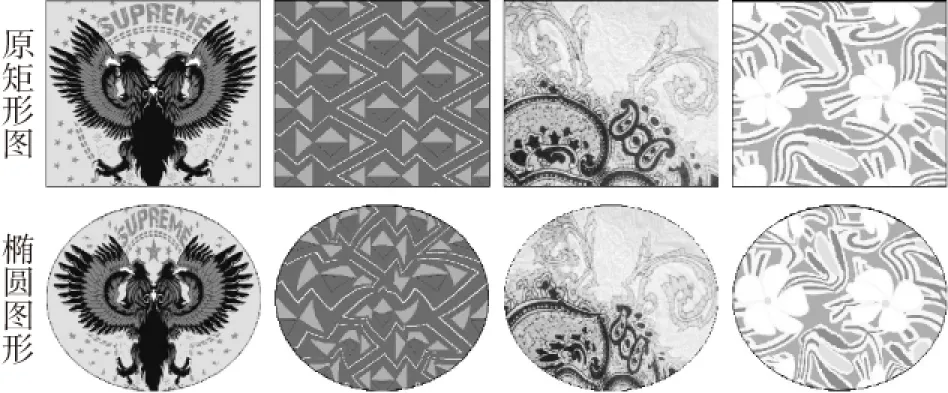
(a) (b) (c) (d)图4 不同图案的椭圆变形效果
从图案整体上看,图案变形只是改变图案的形状和轮廓,并未对图案色彩、纹理等造成任何不利影响,反而给人新颖感;从视觉效果上看,变形后的图案造成周围像素点向图案几何中心点(极点)挤压的视觉感;从像素点上看,像素点变换距离由像素点到中心的距离(OP)和对应相同反正切值的新边界像素点到中心的距离(OM)共同决定。
不同的ON=ρ2(α)坐标方程,得到不同的变形形状。为此,不失一般性,以图4(a)中的原图为例,设定6种类型的曲线方程(a,b为>0的常数,其取值与形变的几何形状无关),结果如图5所示。

y=asin3(α)(a) (b) (c)

y=asin3(α)(d) (e) (f)图5 不同曲线的变形效果
本文算法不仅可以解决一类图案的变形问题,而且变形后的图案保留原有的全部像素点,使得图像的色彩、纹理等内容可以完整地保留。而传统的图像压缩变形算法在变形后的图像中,会出现部分像素点丢失,严重的可能会影响图案的使用,如图6所示。这是由于传统算法中,有些像素点的坐标值经过计算后不可避免地出现小数,而图像处理软件中坐标必须是正整数,因此,必然会对非正整数的坐标数值进行四舍五入运算或直接舍去,造成变形后的图案信息不够完整。本文的算法从数学中函数图像的绘图角度考虑,利用MATLAB软件中surf函数的三维图像的绘图功能(surf函数通常是用来绘制三维彩色图像的)。将像素点计算后的横、纵坐标值看成是surf(X,Y,Z,C)函数的X轴、Y轴的两个参数值(由于本文研究的是平面图像,故Z取值为0),而该点的像素值可以用参数C表示,以此绘制变形后的图案。函数的参数可以是非整数数值,这样就保留了所有的像素点,这是本算法区别与传统算法的最大创新之处。

传统算法 本文算法图6 算法的比较
选取原图几何中心点(原点)作为极点,这是因为从视觉效果考虑对称的因素。而极点的选取是可以根据实际需要改变的,如图7给出了极点在左焦点的椭圆与极点在原点的椭圆比较,可以看出随着极点位置的不同,图像的内容发生变化,像素点按一定的比例依据极点发生相对位置改变,但图像的形状并未发生任何变化。

极点在左焦点 极点在原点图7 不同极点位置的变形效果
4 结语
利用角度变化建立方程,结合surf函数绘图实现图案的各种几何变形,并与传统的变形算法进行比较和分析。结果表明,该方法可以很好地实现不同类型图案的形态变换,有助于图案设计效率的提高,进而在一定程度上提高产品的品质,易获得消费者青睐,也满足当前服饰行业高档时尚的发展需求。此外,该方法的图案几何形变对广告设计、艺术绘画同样具有一定的促进作用,不足之处是对于边界为非规则曲线的方程就很难准确确定,这将是后续研究的重点之一。
[1] 曾双双.几何形态在室内设计中的应用研究[D].长沙:中南林业科技大学,2014.
[2] 杨晓英.几何形态在现代家具设计中运用研究[D].长春:吉林大学,2016.
[3] 时永杰.基于等边三角形网格的交互式二维图像变形技术[D].昆明:云南大学,2013.
[4] 黄 武,姚淑波,关胜亮,等.利用控制线段的实时图像变形方法[J].计算机辅助设计与图形学学报,2010,22(12):2 067-2 072.
[5] 杨金钟,刘政凯,俞能海,等.基于控制点的图像变形方法及其应用[J].中国图像图形学报,2001,6(11):1 070-1 074.
[6] 冯伯乐.织物图像变形技术的研究[D].杭州:浙江大学,2008.
[7] 肖红光,肖树根,刘 净,等.多特征图像融合技术[J].中国图像图形学报,2014,19(7):1 012-1 020.
[8]ChenPengfei,WangJing.Imagedeformationbasedoncontour[J].JournalofComputationalInformationSystems,2014,10(20):8 637-8 643.
[9]CAtanasoaei,FMoldoveanu.ExtensionstotheMLSmethodforimagedeformation[J].JournalofMathematicalImage&Vision,2012,42(1):50-63.
[10]陈 鸿.人脸图像变形技术研究[D].昆明:昆明大学,2013.
[11]AlexandraNasonova,AndreyNasonov,AndreyKrylov,etal.Imageanalysisandrecognition[M].Berlin:SpringerInternationalPublishing,2014.
[12]MShahidFarid,ArifMahmood.ImagemorphinginfrequencyDomain[J].JournalofMathematicalImagingandVision,2012,42(1):50-63.
[13]王 松,朱正平,杨景玉,等.基于图像变形的全景平滑漫游算法研究[J].兰州交通大学学报,2014,33(3):82-86.
[14]张 军,戴 霞.基于图像变形融合时空域滤波的视频微运动增强算法[J].计算机科学,2015,42(6):175-179.
[15]张 铮,徐 超,任淑霞,等.数字图像处理与计算机视觉:2版[M].北京:人民邮电出版社,2014.
Geometrical Distortion of Dress Pattern Based on Angle Variation
GAO Xian-ke,XU Liao-yuan*,XU Ping-hua,ZHOU Jia
(School of Textile and Clothing, Nantong University, Nantong 226019, China)
Based on the design requirement of dress pattern, multiple geometric distortion of pattern was realized by angle variation theory and function plotting knowledge. First determining pixel position that was relative to the pattern center point, according to angle variation establish geometric curve equation which was relative to the pattern center, and determining new coordinate position of the pixel based on scale coefficient and distance from new pixel to center, diverse geometric pattern distortions were finally obtained. The design processing efficiency and appearance effects of traditional pattern were improved to meet the requirement of the pattern design of fashion industry.
pattern; angle variation; geometric distortion; equation
2016-10-11
江苏省大学生实践创新项目(201610304051Z);南通大学纺织服装学院研究生自主创新项目(FZ201507)
高先科(1989-),男,硕士研究生,研究方向:纺织品数字化研究。
*通信作者:徐蓼芫(1957-),女,副教授,硕士生导师,E-mail:xu.ly@ntu.edu.cn。
TS941.2
A
1673-0356(2017)01-0052-04

