圆心设站测设平曲线的精度分析

罗清松，王涛，卢燚

(1.四川化工职业技术学院信息工程系，四川 泸州 646005； 2.泸州职业技术学院建筑工程系，四川 泸州 646005)

圆心设站测设平曲线的精度分析

罗清松1*，王涛2，卢燚1

(1.四川化工职业技术学院信息工程系，四川 泸州 646005； 2.泸州职业技术学院建筑工程系，四川 泸州 646005)

圆心设站测设曲线是近年提出来的道路平曲线测设方法。基于检验该方法测设结果的可靠性，对不同精度等级全站仪使用该方法测设道路平曲线的测设结果进行分析，其结果表明圆心设站测设曲线的精度完全满足现行规范所规定的桩位限差要求。

曲线测设；圆心设站；平曲线；精度分析

1 引 言

圆心设站测设平曲线是由文献[1]提出的，针对自由设站极坐标法测设曲线的一种特殊情况，它是在平曲线圆心上架设全站仪采用极坐标法一次性完成平曲线的测设。它不需要自由设站测设曲线方法中的坐标转换，而是通过两次余弦定理和一次正弦定理，建立一个数学模型从而计算出放样的极角和极距，大大减少了计算的工作量。相比其他放样方法，偏角法存在误差积累，切线支距法、弦线支距法计算复杂，使用麻烦，工作量大的特点[2]，圆心设站测设曲线的方法具有独特的优势，例如该方法所用公式具有规律性，适合计算机及计算器编程；由于放样各相邻点之间没有联系，所以放样点之间没有误差积累，提高了放样点的点位精度。因而本文对该方法放样精度进行研究，通过不同精度等级的全站仪使用圆心设站测设道路平曲线的精度进行分析，验证该方法测设结果是否满足相关规范中的有关要求。

2 圆心设站测设平曲线原理

文献[1]中所述的圆心设站测设平曲线的方法，即为全站仪在圆心上设站，然后通过后视ZH点(或HZ点)，转角一定的角度(极角μi)，定向后再距离放样一定的距离(极距di)，则可确定平曲线的中桩点Pi位置，如图1所示。

图1 圆心设站测设平曲线原理

在圆心设站放样带有缓和曲线的平曲线中桩位置时，将放样元素计算分为缓和曲线和圆曲线两部分。其中缓和曲线放样元素(极距和极角)为：

μi=arcsin(GPisinηi/OPi)

圆曲线放样元素(极距和极角)为：

di=OPi=R

其中对GO、GPi、ηi、∠OGV的计算已由文献[1]中做出相应介绍，在此不阐述。li为ZH(HZ)点到Pi点的长度，l0为缓和曲线长度，L为曲线总从长度，R为圆曲线半径。

3 圆心设站测设平曲线的精度分析

3.1 极坐标法测设圆心点精度分析

圆心设站测设平曲线的精度分析实质为全站仪两次采用极坐标法放样圆心点和平曲线中桩点位的纵向和横向偏差大小的分析。

在放样圆心点时，可采用极坐标法、双测站前方交会法等方法进行测设。本文选择放样精度相对较低的极坐标法进行精度分析及参与后续计算。

如图2，JD点往往是已知的。如果在JD点架设全站仪，则可后视平曲线起点(ZH点)或端点(HZ点)，然后根据现场情况左转或右转180°-α/2(β角，见图2)，距离放样R+E便可得出圆心点。当然如果现场有其他控制点，也可以将该控制点作为后视点，极角或极距则可通过简单的计算得出。

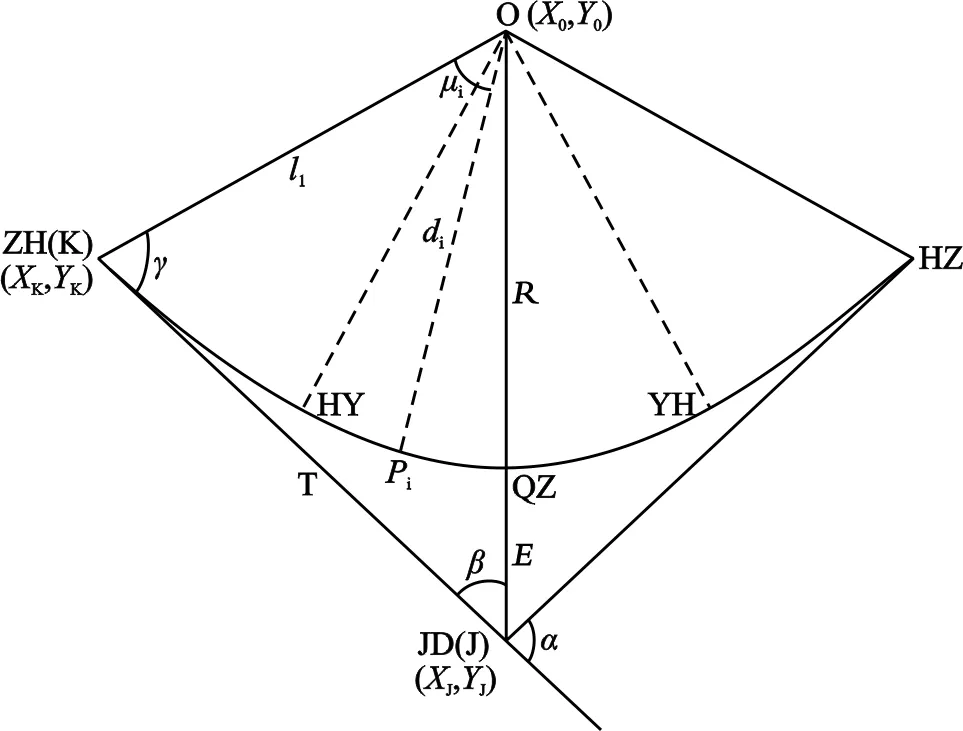
图2 圆心设站测设平曲线精度分析

设JD点坐标为(XJYJ)、ZH点坐标为(XKYK)、圆心O的坐标为(X0Y0)，JO边的方位角为αJO，β=(180°-α)/2，D=R+E，如图1，则：

(1)

将式(1)求全微分得：

(2)

上式由误差传播定律可得：

(3)

式中：mX0、mY0——放样圆心点纵向、横向误差；

mD——测距中误差，即全站仪的标称测距精度；

mαJO——即全站仪的标称测距精度mβ；

ρ=206265″

3.2 圆心设站测设平曲线的误差分析

假设本次放样(包括平曲线圆心和平曲线中桩点放样)使用的全站仪标称测角精度为mβ，标称测距精度为mD，则由上文放样圆心点中误差推导公式可知：

(4)

式中：mXPi、mYPi、mPi——平曲线中桩点Pi纵向误差、横向误差、点位中误差；

αJO、αOPi——JD点到圆心点、圆心点到平曲线放样点的方位角；

mdi——全站仪标称测距精度(式中mD=mdi)；

mαOPi——全站仪标称测角精度mμi(式中mαJO=mαOPi=mμi)。

4 不同精度等级全站仪测设精度计算分析

当我们对某个量进行观测时，总是会受到对中误差、操作误差、测角误差、测距误差、频率误差、大气折光和地球曲率等的影响。这些影响中的每一个都会引起基本误差项，而某个量总的测量误差则是这些影响引起的基本误差项的总和。如果每个基本误差项对其总和的影响是均匀的小，那么对某个量进行测量的误差是服从正态分布的随机变量。按照测量误差理论[4]“绝对值大于二倍中误差的偶然误差出现的概率为4.5%，特别是绝对值大于三倍中误差的偶然误差出现的概率仅为0.3%”的特性，工程实践中常取2倍中误差为测量的桩位偏差。则式(4)可整理为：

(5)

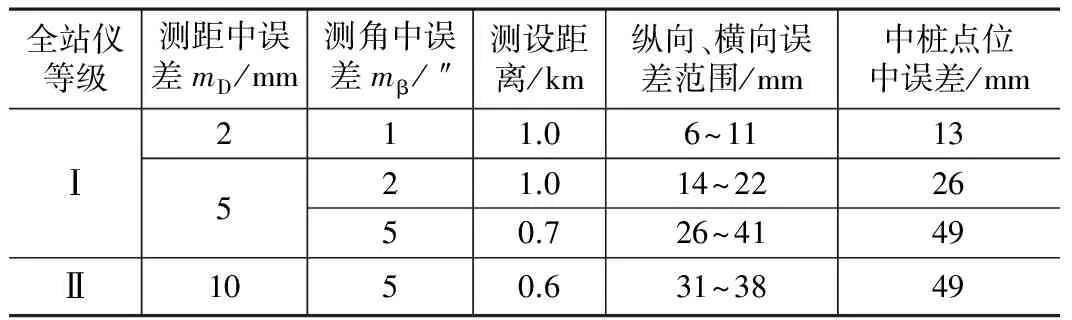
平曲线中桩桩位误差由圆心点误差和极坐标法放样平曲线误差累积而来，由式(5)可知，影响平曲线放样点误差的因子有JO的方位角和长度，OPi的方位角和长度。考虑到平曲线放样点中误差影响因子较多，为了便于分析，本文将测设圆心点的纵横向误差的最大值引入平曲线中桩桩位误差公式中进行分析。文献[3]和文献[6]都提出了，放样点误差随着极距的增大而增大，为了控制放样点误差，极坐标法放样距离应控制在 500 m以内。则选取极距为 500 m，引用该情况下不同精度等级全站仪放样出的圆心点的纵向和横向误差最大值进行后续分析。依据《公路勘测规范》对光电测距仪器的分级标准和当前公路建设单位常用全站仪类型和精度指标，通过式(3)(D=500 m)可计算出不同精度等级全站仪随着方位角的变化测设出的圆心点纵向和横向偏差(误差)最大值，如表1所示[6]。

不同精度等级全站仪放样圆心点的纵向、横向最大误差计算结果 表1

结合式(5)、表1可得出放样点Pi的横向和纵向误差应有以下关系：

(6)

此处便将(6)式的“小于”号默认为“等于”号(即圆心点纵向和横向误差取其最大值)进行后续分析，则通过该式可以导出不同精度等级的全站仪采用圆心设站法测设平曲线的桩位纵向和横向误差(偏差)计算公式，如表2所示。

圆心设站放样平曲线桩位的纵向和横向误差计算公式 表2

从表2的计算公式中可以看出，影响平曲线桩位的纵向和横向误差的因素便缩减为两个，分别为平曲线放样的测设距离和方位角。则选取不同的测设距离和方位角大小计算出不同精度等级全站仪测设中桩桩位时的纵横向允许误差、桩位点位中误差与测设距离、方位角间的关系，如图3～图6(图中X轴为方位角(弧度制)，Y轴为测设距离(极角)，Z轴为误差大小)。

《公路勘测规范》中对放样点点位及纵向和横向限差有明确的规定(以平原微丘高速公路、一级公路为例)，桩位限差不应超过以下规定：

中桩位置中误差：±5cm

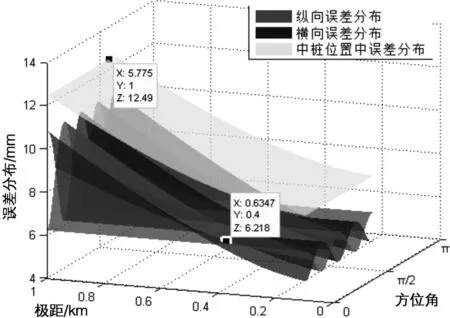
图3 Ⅰ级全站仪(mD≤±2 mm，mβ≤±1″)测设平曲线桩位误差分布

图4 Ⅰ级全站仪(mD≤±5 mm，mβ≤±2″)测设平曲线桩位误差分布

图5 Ⅰ级全站仪(mD≤±5 mm，mβ≤±5″)测设平曲线桩位误差分布

图6 Ⅱ级全站仪(mD≤±10 mm，mβ≤±5″)测设平曲线桩位误差分布

横向误差：±5 cm

则从图3～图6可以得出：

①表3是根据图3～图6的统计所得。按《公路勘测规范》规定的限差要求，使用圆心设站测设平曲线时，Ⅰ级全站仪(mD≤±5 mm，mβ≤±5″)的测设距离应控制在 700 m以内，Ⅱ级全站仪(mD≤±10 mm，mβ≤±5″)测设距离应控制在 600 m以内。但如果使用Ⅰ级全站仪(mD≤±5 mm，mβ≤±2″及mD≤±2 mm，mβ≤±1″)则测设距离可达 1 km以上，考虑到在使用仪器中其他误差的影响，也完全能够满足《公路勘测规范》中的各项限差要求。

圆心设站放样平曲线中桩误差统计 表3

②随着测设方位角的增大，桩位纵向误差变化具有余弦函数规律；桩位横向误差具有正弦函数规律。但随着测设边长的增加正余弦函数的振幅将变小。不同精度等级全站仪有个不同的测设距离，使得纵横向误差的振幅将变得一样，此时，桩位的纵横向误差不受方位角大小的影响，因而为了减少方位角测设误差的影响，Ⅰ级全站仪(mD≤±2 mm，mβ≤±1″)、Ⅱ级全站仪(mD≤±10 mm，mβ≤±5″)测设距离在 400 m左右为宜，Ⅰ级全站仪(mD≤±5 mm，mβ≤±2″)测设距离在 500 m左右为宜，Ⅰ级全站仪(mD≤±5 mm，mβ≤±5″)测设距离在 200 m左右为宜。

5 结 论

本文对圆心设站测设道路平曲线的测设精度进行了分析，结果表明只要正确规范的使用不同精度等级的全站仪，圆心设站法测设道路平曲线桩位的各项误差便能完全符合《道路勘测规范》的限差要求。因而该方法在合适的施工条件下，值得推广。

[1] 罗清松，罗尧东. 圆心设站测设曲线的实用方法研究[J]. 城市勘测，2013(3)：146～149.

[2] 张正禄，李广云，潘国荣等. 工程测量学[M]. 武汉：武汉大学出版社，2005.

[3] 赵一飞. 极坐标法放样公路中线的精度保证[J]. 交通科技，2003(4)：34～36.

[4] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉：武汉大学出版社，2009.

[5] JTJC10-2007. 道路勘测规范[S].

[6] 张还在. 用全站仪测设公路平曲线的精度分析[J]. 内蒙古交通运输，2008(2)：17～19.

[7] 彭仪普. 任意站极坐标法测设线路平面曲线探讨[J]. 铁道工程学报，2001(3)：11～13.

[8] 谯生有. 缓和曲线坐标计算误差分析[J]. 测绘通报，2001(11)：38.

[9] 杨存吉，李全信. 线路中线测设的统一数学模型[J]. 测绘通报，2001(2)：14～15.

[10] 高利平，刘霖，林敏等. 带缓和曲线的长大曲线实用测设方法研究[J]. 中国公路学报，2002，15(4)：25～27.

Accuracy Analysis of Surveying and Designing the Curve on the Center

Luo Qingsong1，Wang Tao2，Lu Yi1

(1.Department of Information Engineering，Sichuan Vocational College of Chemical Technology，Luzhou 646005，China； 2.Department of Architecture，Luzhou Vocational Technical College，Luzhou 646005，China)

Surveying and designing the curve on the center is proposed in recent years. Surveying the results of the test method based on reliability，this article indicates that different accuracy obtained in surveying of horizontal curve can meet fully the requirements form of error stipulated in current edition of specifications.

arrangement of curve；survey on the center；horizontal curve；accuracy analysis

1672-8262(2017)01-111-05

P258

B

2016—07—07 作者简介：罗清松(1990—)，男，助理工程师、助教，研究方向：工程测量、摄影测量等。