基于三次样条曲线拟合的激光拉曼光谱基线校正研究

聂 磊， 陶 明 ， 翟中生

(湖北工业大学机械工程学院， 湖北 武汉 430068)

基于三次样条曲线拟合的激光拉曼光谱基线校正研究

聂 磊， 陶 明 ， 翟中生

(湖北工业大学机械工程学院， 湖北 武汉 430068)

拉曼光谱基线校正是拉曼分析技术的重要环节，特别是将拉曼光谱用于定量分析时，光谱基线校正的准确性直接影响定量分析的精度。三次样条函数具有平滑作用，拟合的数值稳定而且具有较好的收敛性。用其校正拉曼光谱基线，既能对拉曼光谱基线进行拟合，又能突出三次样条曲线对基线的平滑作用，达到一定去噪功能，提高拉曼光谱的信噪比，为拉曼光谱基线校正提供了一种有效方法。将三次样条函数应用于某种炔烃化合物气体拉曼光谱的基线校正，采用单峰法和三点面积法计算拉曼光谱强度，实验结果证明，分段三次样条曲线拟合达到了理想的基线校正效果，而且相比其他方法其误差最小。

拉曼光谱；信噪比；三次样条函数；内标法

拉曼光谱包含探测试样的有关分子信息，是分子极化率改变的结果,被称为分子的“指纹谱”[1]，其分析技术不需要对试样进行预处理,具有非破坏性、快速高效的优点，因此得到广泛应用。但是，由于受到环境噪声和荧光背景的影响[2]，拉曼光谱会产生基线漂移、峰值位置不准确等现象，给其分析带来不利影响[3]。特别是在定量分析中，基线漂移会造成拉曼特征峰峰高或峰面积无法准确计算，无法标定拉曼峰值强度与物质浓度之间的关系[4]，给定量分析带来困难[5]。

拉曼光谱基线校正的方法主要包括导数法、小波变换法、平滑法等[6]。常用的基线校正方法是根据噪声和背景的特点，对拉曼光谱数据采用不同的方法进行重构，分离出基线信号和光谱信号，然后去除基线信号，达到基线校正的效果。但这种方法在分离基线和光谱信号时，有许多参数需要人为设定，对原始光谱干涉比较大，导致拉曼光谱数据在一定程度上失真，而且分离和复现数据麻烦，有时会放大噪声，甚至会改变拉曼光谱曲线的形状[7]，影响预测模型的精度。基线校正的另一种常用方法是对基线采用多项式曲线拟合，但是此方法对拟合阶数难以确定，若阶数选取不当则无法得到理想的校正效果[8]。因此，本文针对上述问题，提出一种基于三次样条函数的基线校正方法，利用三次样条曲线分段拟合拉曼光谱基线，保留了拉曼光谱数据的原始信息[9]，克服了人为干涉光谱信号的问题，又利用三次样条曲线的平滑特点，进一步对光谱信号做平滑去噪处理,从而得到了比较理想的校正效果。

1 分段拉曼光谱基线校正原理

每一种物质的拉曼光谱特征峰个数和位置不尽相同，在对其进行基线校正时，要尽可能保留特征峰信息，可采用拉曼光谱特征峰分段的处理方法[3]。将拉曼光谱分为波峰区间和非波峰区间，根据光谱仪CCD像素值与波数之间的对应关系、两波峰之间的距离，选择保留各个特征峰峰值点前后的数据点(一般选择前后各5点)作为波峰区间[10]，非波峰区间则处在波峰区间两侧。非波峰区间的光谱信号，由于不含分析物质的特征光谱信息，可以直接作为基线处理[11]，对于波峰区间的光谱信号，包含了基线信号，需要将基线去除实现校正[12]。其具体方法是，对波峰区间前后两侧的非波峰区间信号进行曲线拟合，得到拟合的基线曲线，再将波峰区间点代入到拟合曲线中，得到波峰区间基线信号强度值，最后用波峰区间拉曼光谱强度值减去拟合的基线信号强度值，即可得到基线校正后的波峰区间信号。

分段拉曼光谱基线校正的方法不但避免了分离背景噪声的处理步骤，更能对每个波峰区间进行单独分析，比较完整地保留了非峰值区间基线的真实数据，这样实现了拉曼光谱特征峰数据的真实性与准确性，从而达到提高拉曼光谱信噪比的效果。

1.1 分段三次样条曲线拟合基线方法

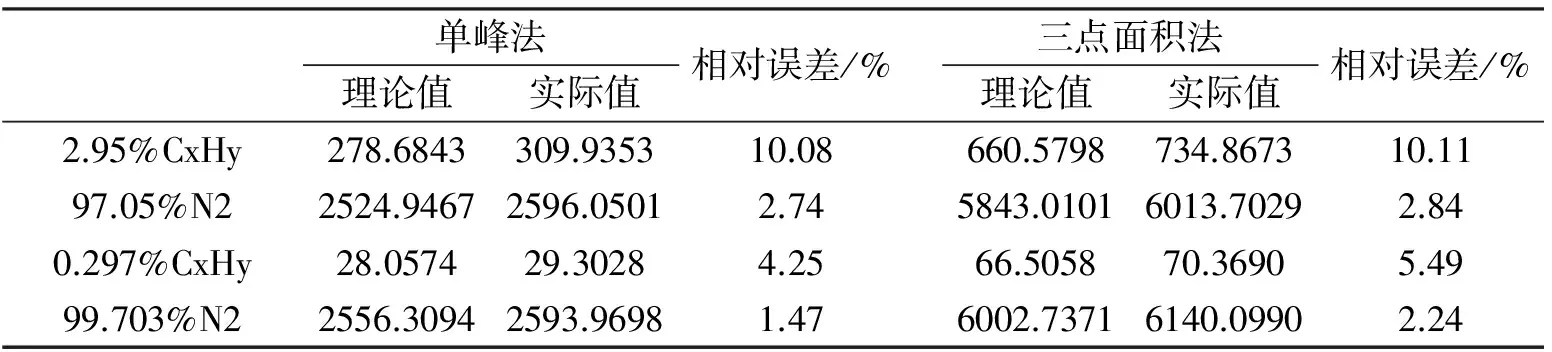
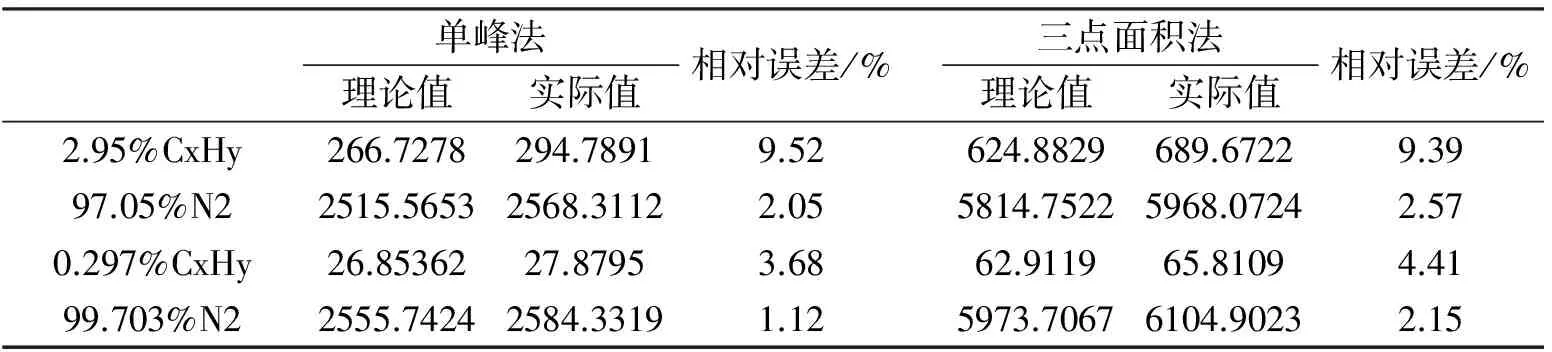
若函数s(x)∈C2[a,b]，且在每个小区间[xj,xj+1]上是三次多项式，其中a=x0

s(xj)=yj(j=0,1,…,n)

(1)

成立，则称s(x)为三次样条插值函数。要求出s(x),每个小区间[xj,xj+1]上要确定4个待定系数，共有n个小区间，故应确定4n个参数，根据s(x)在[a,b]上二阶导数连续，在节点xj(j=1,2,…,n-1)处应满足连续性条件

s(xj-0)=s(xj+0)

(2)

s′(xj-0)=s′(xj+0)

(3)

s″(xj-0)=s″(xj+0)

(4)

共有3n-3个条件，再加上s(x)满足式(4)插值条件，共有4n-2个条件，则还要2个条件才能确定s(x)，考虑采用分段拉曼光谱基线校正方法，要满足分段处的首尾两端点x0和xn各与其前后基线连接具有连续性和光滑性，在首尾分段点处各加一个条件，使分段首尾两端点满足三次样条第一类边界条件，但是理想实验环境下基线信号应该是一个稳定的数值，f′(xj)=0，则加入的边界条件满足

s′(x0)=f′(x0)=0

(5)

s′(xn)=f′(xn)=0

(6)

联合式(1)、(2)、(3)、(4)、(5)、(6)即可得到三次样条函数。

采用三次样条函数对拉曼光谱基线分段校正，根据三次样条曲线本身的光滑性，能够保证校正后的基线具有光滑连续性。

1.2 浓度求取原理

在气体成分的测试中，对校正后的拉曼光谱曲线，采用内标法[13]测量被测气体拉曼峰值强度与浓度之间的关系。通常选取N2为标定气体，主要是因为N2特征峰相对稳定，信号较强，而且一般与被测气体的拉曼谱峰没有重叠。试验对定制浓度的被测气体进行标定，标定过程将被测气体的光谱强度统一转化成N2的光谱强度，然后根据N2的拉曼峰值强度和浓度之间成正比关系，即可得出被测气体的拉曼峰值强度与浓度的关系。

用N2作为内标物，需要知道单位浓度N2和单位浓度被测气体的拉曼峰值强度之比，即被测气体峰值强度转换成N2峰值强度的转换系数[14]，简称拉曼效率比(Ramanefficiencyratio)，根据每种气体固有的分子特性，拉曼效率比在同一条件下理论上是定值，拉曼效率比

(7)

式中：HN、HU分别表示N2和被测气体标定时的光谱强度，DN、DU分别表示N2和被测气体标定时的浓度。

若已知h为测量的被测气体拉曼峰值强度，d为测量时被测气体的浓度，K2为N2拉曼峰值强度与其浓度之间的线性比例系数。则被测气体的拉曼峰值强度与浓度之间的关系

d=K1K2h

(8)

由此可见，只有准确标定被测气体转换成N2峰值强度的拉曼效率比K1，才能准确得到被测气体拉曼峰值强度与浓度的关系，而标定K1的准确性与基线校正的好坏有很大关系。

2 实验

为了验证分段三次样条曲线拟合基线处理方法的效果，对炔烃化合物与N2的混合气体进行了拉曼光谱数据采集。计算基线校正后单位浓度(即炔烃化合物在混合气体中的浓度为1%)下混合气体的拉曼光谱强度，并利用该值预测其他浓度的同种混合气体拉曼光谱强度；比较预测值与实际测得值，计算相对误差，与常用的最小二乘法多项式拟合基线方法进行对比，发现三次样条曲线拟合基线方法相对误差最小，校正效果更佳。

2.1 实验系统

光谱仪采用Ocean Optics公司的QEPB6500，其感光器件CCD是1044个像素的线性阵列，对应其拉曼光谱测量范围537.38～738.43 nm。激光器采用532 nm单色激光，激光器波长不在光谱仪测量范围内,避免瑞利散射对拉曼散射的影响[15]。

2.2 实验设计

实验系统压强为0.5 MPa，采集不同浓度被测气体和N2混合气体的拉曼光谱数据。混合气体的体积分数如表1所示，每一组数据采集100次取平均值作为最终拉曼光谱数据。

表1 混合气体成分

被测气体存在多个拉曼谱峰，计算拉曼峰值强度时选择主峰作为目标峰[16]，其拉曼频移在1 984 cm-1处，对应的位置在594.62 nm处，N2的主峰拉曼频移在2 331 cm-1，对应的波长在607.45nm处。

实验以混合气体①作为标定气体，分别采用分段最小二乘法二阶、三阶多项式，分段三次样条曲线对基线进行拟合校正，计算被测气体与N2的拉曼峰值强度。拉曼峰值强度的计算方法采用单峰法和三点面积法[17]，单峰法即直接选取波峰区间的峰值点作为拉曼峰值强度，三点面积法即累加波峰区间的峰值点及其左右两点的值作为拉曼峰值强度，在数字信号中累加即可代表面积。

计算混合气体①的拉曼峰值强度后，求取单位浓度被测气体以及单位浓度N2的拉曼峰值强度，并以此值为依据，预测混合气体②以及混合气体③的拉曼峰值强度理论值。实验中采集的混合气体②和混合气体③拉曼光谱数据，直接采用分段最小二乘法二阶、三阶多项式，分段三次样条曲线对基线进行拟合校正，并用单峰法和三点面积法计算拉曼峰值

强度作为实际值，比较理论值与实际值并计算其相对误差[18]，以此对比各种基线校正方法的效果。

3 结果与讨论

图1是混合气体①在积分时间3 s，采用分段三次样条曲线对基线进行拟合校正后的结果，图中可以看到原始拉曼光谱数据由于受到噪声影响，基线不仅不平滑而且还具有一定的高度，不在水平坐标轴上，这样的数据不能计算拉曼峰值强度且不能进行定量分析，必须进行基线校正，使基线与水平坐标轴重合。

图 1 被测气体和N2混合气体拉曼光谱基线校正

单峰法理论值实际值相对误差/% 三点面积法理论值实际值相对误差/%2．95%CxHy278．5805309．604710．02660．2700733．880710．0397．05%N22532．96352593．67972．345867．04576024．57762．610．297%CxHy28．046929．77625．8166．474670．69275．9799．703%N22564．33782602．20571．486027．42986179．16982．46

图2是混合气体①在积分时间3 s时原始拉曼光谱图以及采用分段三次样条曲线拟合基线，分段最小二乘法二阶、三阶拟合基线图。图3是采用不同基线拟合方法拟合被测气体主峰处的基线效果图。

图 2 混合气体拉曼光谱基线拟合图

图 3 被测气体拉曼主峰处基线拟合图

从图3可以看出，分段最小二乘法拟合拉曼光谱基线，其拟合结果是基于拟合光谱基线与实际光谱基线之间的最小误差。此种方法在一定程度上保持了原始拉曼光谱基线信号信息，但是无论二阶或三阶基线拟合，其效果与原曲线均存在较大差异，容易出现欠拟合和过拟合现象[14]。而图3中分段三次样条曲线拟合基线最大程度保持了原始拉曼光谱基线信号信息，因此拟合出的峰值区域基线较为准确，充分体现了分段三次样条曲线平滑的优点。

对混合气体①基线校正后，利用单峰法和三点面积法计算出单位浓度被测气体和单位浓度N2的拉曼峰值强度，预测混合气体②和混合气体③拉曼峰值强度理论值，并对实际测得的混合气体②和混合气体③拉曼光谱数据，采用对应的方法进行基线拟合校正，计算被测气体拉曼峰值强度实际值，其数据如表2所示。

通过数据对比发现，无论是采用峰值法还是三点面积法，分段三次样条曲线对基线拟合校正，其校正后预测的理论值与实际值相对误差最小，而采用分段最小二乘法对基线进行拟合校正，其相对误差都大于分段三次样条曲线拟合校正后的相对误差。其原因有以下几点。

表3 压强0.5 MPa，积分时间3 s分段最小二乘法三阶拉曼光谱基线校正

表4 压强0.5 MPa，积分时间3 s分段三次样条曲线拉曼光谱基线校正

其一，分段最小二乘法拟合基线是基于拟合最小误差理论。理想实验环境下，虽然可以把拉曼光谱基线看作一个稳定值，但是实际实验环境中基线信号还是会轻微波动。采用分段三次样条曲线拟合基线，在光谱仪采集的数据点上保留了基线信号信息，在非数据采集点上，插值出基线信号值，这样最大程度逼近了实际实验环境的基线信号信息。

其二，采用分段拉曼光谱基线校正时，拟合的区间只包括波峰区间左右两侧，中间的波峰区间被隔离，会出现数据的突变，且分段后每一段基线的特点各不相同，但是基线信号只是轻微波动，拟合出的波峰区间两侧基线应该具有光滑连接的特点。采用分段最小二乘法基线拟合校正，做到的只是在一定程度上保持了原始拉曼基线信号信息，并没有保证分段拟合基线连接的光滑性，会使拟合出的基线效果不够理想。而三次样条曲线具有二阶光滑度，即有二阶连续导数，比最小二乘法曲线拟合的光滑性好，其本质是分段的三次多项式拼合而成的曲线，在拼接处不仅函数是连续的，且一阶二阶导数也是连续的[9]，采用分段三次样条曲线拟合基线会实现基线连接平滑过渡的作用。

综上，采用分段三次样条曲线拟合校正拉曼光谱基线信号，不仅最大限度保留了原始拉曼光谱基线信号信息，还能对基线进行平滑作用，拟合出的峰值区域基线十分理想，从而达到进一步去噪功能，提高了拉曼光谱的信噪比。

4 结论

分段三次样条曲线拟合校正拉曼光谱基线，不仅能使拟合基线更加真实，还使基线更加平滑，拟合出的峰值区域基线效果较为理想，既满足了一定去噪功能，又保证了后面拉曼光谱数据定量分析的准确性。因此，基于三次样条的拉曼光谱基线校正方法的提出，为激光拉曼基线校正提供了一种有效的参考方法。

[1] 李津蓉. 拉曼光谱的数学解析及其在定量分析中的应用[D]. 杭州：浙江大学, 2013：20-21.

[2] 高国明, 李雪, 覃宗定,等. 消除拉曼光谱荧光背景的新方法及其应用[J]. 光学学报, 2013, 33(2):258-266.

[3] 林漫漫，牛丽媛，覃赵军，等.分段式线性拟合校正拉曼光谱基线漂移[J]．光子学报，2012，41(1)：112.

[4] 张保华, 江永成, 沙文,等. 特征提取算法在福美双表面增强拉曼光谱定量分析中的应用[J]. 光谱学与光谱分析, 2015(2):390-393.

[5] 阮华, 戴连奎, RuanHua,等. 支持向量机分类与回归联合建模方法及其在拉曼光谱分析中的应用[J]. 仪器仪表学报, 2010, 31(11):2440-2446.

[6] 郭忠, 廖海洋, 陈益,等. 一种改进小波阈值函数在拉曼光谱去噪的应用[C]// 2009全国虚拟仪器大会论文集(一). 2009.

[7] 杨桂燕, 李路, 陈和,等. 基于广义Whittaker平滑器的拉曼光谱基线校正方法[J]. 中国激光, 2015(9):360-368.

[8] 高鹏飞, 杨蕊, 季江,等. 拉曼光谱的局域动态移动平均全自动基线校准算法[J]. 光谱学与光谱分析, 2015(5):1281-1285.

[9] 张玲.基于三次样条曲线拟合公路平面线形方法研究[D].武汉：武汉理工大学，2007.

[10] Jr C H C, Cicerone M T. Chemically sensitive bioimaging with coherent Raman scattering[J]. Nature Photonics, 2015, 9(5)：295-305.

[11] 高小玲. 应用拉曼光谱法进行定量分析的几个关键性技术问题[J]. 分析试验室, 1995(4):52-56.

[12] 李庆波, 于超, 张倩暄. 基于净信号的乙醇含量拉曼光谱分析方法研究[J]. 光谱学与光谱分析, 2013, 33(2):390-394.

[13] 陈玉锋, 庄志萍, 魏林博,等. 激光拉曼光谱内标法直接测定甲醇含量[J]. 理化检验-化学分册, 2015, 51(4):558-559.

[14] Hansen S B, Berg R W, Stenby E H. High-pressure measuring cell for Raman spectroscopic studies of natural gas[J]. Applied Spectroscopy, 2001, 55(1): 55-60

[15] 姜承志, 孙强, 刘英,等. 基于多尺度局部信噪比的拉曼谱峰识别算法[J]. 光学学报, 2014, 34(6):299-305.

[16] Alfonso-García.Alba,Mittal.Richa ,Lee.Eun Seong,Potma.Eric.O. .Biological imaging with coherent Raman scattering microscopy :A tutorial .Journal of Biomedical Optics, v 19, n 7, July 2014，19(7)：071407.

[17] Seruga B, Pond G R, Hertz P C, et al. Comparison of absolute benefits of anticancer therapies determined by snapshot and area methods[J]. Annals of oncology, 2012, 23(11):2977-2982.

[18] 费业泰. 误差理论与数据处理[M]. 北京：机械工业出版社，2006：57-73.

[责任编校： 张 众]

Correction of Raman Spectroscopy Baseline Based on Cubic Spline Curve Fitting

NIE Lei, TAO Ming, ZHAI Zhongsheng

(SchoolofMechanicalEngin.,HubeiUniv.ofTech.,Wuhan430068,China)

The baseline correction is an important step in the Raman analysis technology, especially in the Raman spectroscopy for quantitative analysis. Whether the Spectral baseline correction is good or not directly affects the accuracy of quantitative analysis. With the capability of smoothing data curve, cubic spline function can realize stable fitting curve which has good convergence. Thus, cubic spline fitting is a proper baseline correction method for Raman spectroscopy. It can not only fit the spectroscopy curve, but also improve the signal-to-noise ratio. Using the baseline correction method, the Raman spectroscopy of an alkyne gas mixed with N2was processed. Single peak and the three-point area methods were applied to calculate the intensity of the Raman spectrum. The experimental result shows that the cubic spline fitting correction method achieves satisfactory effect and has the relatively low error.

Raman spectroscopy; signal-to-noise ratio; cubic spline function; internal standard method

2016-10-15

湖北省科技支撑计划(142142407)

聂 磊(1978-)，男，湖北武汉人，工学博士，湖北工业大学副教授，研究方向为电子制造工艺可靠性

1003-4684(2017)01-0063-05

O657.3

A