基于精英协同的多种群分布估计算法
周 丹 谢 敏 刘 方 韦 剑
(南京邮电大学通达学院计算机工程系 江苏 扬州 225127)
基于精英协同的多种群分布估计算法
周 丹 谢 敏 刘 方 韦 剑
(南京邮电大学通达学院计算机工程系 江苏 扬州 225127)
针对传统分布估计算法局部搜索能力弱,易陷入早熟收敛的问题,在分布估计算法的基础上引入精英策略并采用划分子种群独立进化的方式,提出一种基于精英协同的多种群分布估计算法。该算法混合了两种后代产生的策略:一种是进化过程采用精英协同操作用于进行局部搜索并开辟出新的搜索空间,另一种是采用划分子种群独立进化方式保证种群间个体的多样性。基准测试函数实验结果表明,该算法在收敛性和多样性方面均表现出明显优势。
分布估计算法 早熟收敛 精英协同 子种群
0 引 言
多目标优化问题在工程实践和科学研究中一直是非常重要的研究课题之一[1],现实生活中的优化问题往往受到多个相互冲突目标的影响,该类多目标优化问题存在一个Pareto[2]最优解。为了研究解决多目标优化问题,国内外学者分别提出了不同的多目标进化算法,比如:NSGA-II[3]、MOPSO[4]、RM-MEDA[5]、NNIA[6]等。
分布估计算法EDA(Estimation of Distribution Algorithm)是一类新型的优化算法。EDA首先采用统计分析的方法对较优秀的个体进行统计分析,然后根据分析结果建立概率模型并通过采样产生下一代解, 最后经过不断的重复统计建模和采样过程,得到问题的最优解。分布估计算法与传统进化算法不同:没有类似遗传算法中的交叉、变异操作,是基于对种群的进化趋势进行统计,根据统计结果建立模型,利用进化思想对建立的模型进行进化。综上,EDA算法是一种“宏观”层面的进化,具有良好的全局搜索能力,但与此同时局部搜索能力不足。
分析EDA局部搜索能力差,易陷入早熟收敛的原因:(1) EDA没有类似于交叉、变异等基于“微观”层面上的进化操作或建模。(2) 在整个进化期间随着进化代数的增加,种群间个体不断接近,降低了种群的多样性。为了解决以上不足,学者们提出了不同的改进方案:Zhang等学者针对多目标优化问题提出了RM-MEDA[5];程玉虎等在传统EDA基础上结合混沌变异操作提出了EDA-DP[7];Madera等结合子种群划分独立进化提出了dEDA[8]。
在上述算法的基础之上,提出一种基于精英协同的多种群分布估计算法。该算法将初始种群的非支配个体根据网格选择,分为两个不同级别的精英种群,两个精英种群协同操作,促进精英个体的进化。将初始种群根据子种群划分,划分为若干个子种群,每一个子种群对应一个概率分布模型,结合子种群精英个体的浓度各自独立的进化,以保证该算法不仅具有更好的全局收敛性,且能够更好地保证种群的多样性。
1 网格选择
为进一步发挥精英个体的优势地位,为每一个非支配解确定级别。首先对种群中个体进行非支配排序,可得到非支配解集合Elite,采用网格选择将非支配解集合Elite分为级别1的精英种群EH和级别2的精英种群EL。
网格选择基本思想如下:为解分配辨识向量的ε支配计算方法[13](ε是一个可以事先预设的参数),在为每一个解分配一个辨识向量,即给该解分配了一个生存区域,划分生存区域的机制可根据解本身的取值来自适应地分配。在进化初期,由于非支配个体较少,可适当将ε的值取大,后期随着进化代数的增加,非支配个体较多,可适当降低ε的取值。
如图1所示,对图中非支配个体进行网格选择,其中个体‘1’、‘2’和‘3’处于同一生存区域内,个体‘2’距它们共同的辨识向量‘A’较近,所以被保留,而‘3’和极端解‘1’由于距A较远而被删除。由于极端解对应某一目标函数的极值,对整个解集的分布和最终决策的选择具有重要意义,所以极端解‘1’不应被删除。最终该区域中‘1’、‘2’都会被保留。该生存区域网格选择结果为:个体‘1’、‘2’定义为级别1种群EH中的精英个体,个体‘3’定义为级别2种群EL中的精英个体。

图1 网格选择示意图
2 子种群划分
传统EDA随着进化代数的增加,种群间个体逐步接近,种群多样性差。为提高算法多样性,将整个种群分成若干个子种群,每个子种群独立的建模进化,设将目标函数空间划分成S个子种群,具体划分方式如下:(1) 种群中全部个体划分到第一象限,为单位超球面选择S个分布均匀的单位向量,S个子种群的中间向量为w1,w2,…,ws。(2) 所有个体结合目标方程计算个体与S个中间向量(w1,w2,…,ws)的夹角,夹角值为(v1,v2,…,vs)若vi(i=1,2,…,s)最小,则将该个体分配给i子种群。
如图2所示二目标为例,将种群分成S(S=6)个子种群。w1,w2,…,w6为S个子种群的中间向量,计算个体A和B与S个中间向量的夹角并进行比较,通过比较将A分配给w5所在的子种群,将B分配给w6所在的子种群。

图2 子种群划分方法
3 精英分级协同进化
为了提高算法的收敛性,级别1精英种群EH和级别2精英种群EL采用协同进化策略[11]推动精英个体的进化。EH内个体采用长方体交叉算子CCOI算子相互协作,产生高质量解;EH对EL进行引导,引导操作时采用CCOI[15]算子,并根据个体之间的距离,离散交叉算子DCO[15]算子、翻转交叉算子FCO[15]算子交互使用,推进相似个体的进化,避免进化陷入局部最优。
3.1 精英协作
精英协作是指两个EH中的个体合作进化,提高父代解质量。CCOI算子中的新个体由式(1)产生,其中λk=U(0,2)。用x和y表示来自EH的两个父代个体,用zu和zv表示中间状态,用u和v分别表示x和y在精英协作之后产生的个体。
(1)
用式(2)判断新产生的个体是否超出解空间的约束范围,未超出解空间的新个体若可支配其父代个体,则更新到子代中。
(2)
3.2 精英引导
精英引导是指一个EH个体对EL个体的引导,促进EL中个体向EH中个体靠近。用x和y表示来自EH和EL的两个父代个体,用zu和zv表示中间状态。用式(2)判断新产生的个体是否超出解空间的约束范围,未超出解空间的新个体若可支配其父代个体,则更新到子代中。


(3)
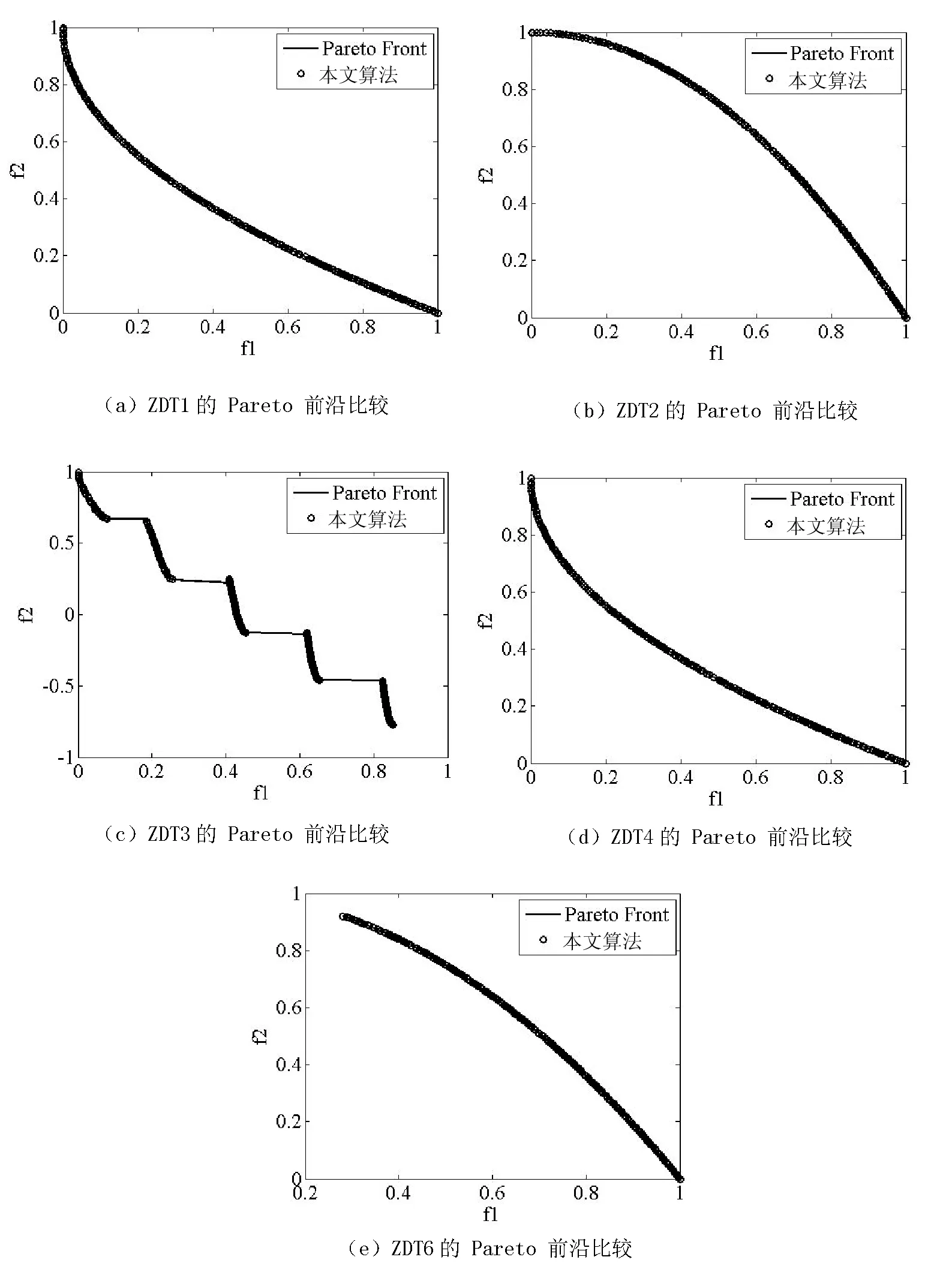
FCO算子中的新个体由式(4)产生,其中1 (4) 为进一步提高传统分布估计算法解决多目标优化问题的性能,本文结合精英协同和多种群划分独立进化,提出一种基于双精英协同的多种群分布估计算法。基本思想如下:一方面采用精英协同思想对种群进行“微观”层面的进化,另一方面各个子种群结合该子种群中精英个体的浓度建模,确定进化的方向和规模,保证种群的多样性。具体算法步骤如下所示: Step1 设置算法中的参数,种群规模为N,设置评价次数Max_e(参考文献[18]中实验设计,Max_e设置为90 000次),当前评价次数Current_e=0(每次使用评价函数后Current_e=Current_e+1,Current_e=Max_e算法结束),交叉概率Pcu=0.4,当前代数t=0,随机产生初始种群Pop(t)。 Step2 通过对种群中个体非支配排序得到精英种群Elite,采用网格选择为精英个体分级为:级别1的精英种群EH,级别2的精英种群EL。 Step3 根据子种群划分得到S=6个子种群,确立各种群中的所有个体。 Step5 通过统计子种群中精英个体浓度确定分布估计算法方向与规模:根据精英个体在各个子种群中分布的浓度确定高斯分布的方向和规模,新生成的种群与父代种群合并个体浓度选取N个个体组成下一代种群Pop(t+1)。算法步骤如下: (1) 子种群进化方向确定:经精英协同操作之后,种群EH和种群EL合并得精英种群ET,采用轮盘赌策略,根据ET种群中个体在各个子种群中分布的浓度比例确定各个子种群被选中建立概率模型的机率。具体如下:设种群数为S,种群ET在各个子种群的总浓度为eTotal=e1+e2+…+es=1,根据ei(i=1,2,…,s)的高低采用轮盘赌策略选择一个子种群建立概率模型,轮盘赌策略原则为:精英个体浓度高的子种群被选中的概率低,精英个体浓度低的子种群被选中的概率高。 (2) 子种群进化规模确定:按建立的概率模型为选定的子种群产生N/ei(i=1,2,…,s)个新的个体。 (3) 后代种群选择:新生成的个体与父代种群根据采用NSGA-II中拥挤距离比较算子[3],选取规模为N的下一代种群Pop(t+1)。 Step6 判断当前评价次数Current_e是否等于Max_e,如果相等算法结束输出种群Pop,否则转入Step2。 5.1 实验设计 何泽说,代价真的不小,给老百姓付成本去了五万,工钱四万,运输和路上的缴费花了近两万,打点关系一万,我这棵树的本钱就花了十四五万。何泽说的数字,完全是自由发挥,让一点都不懂数字和经济的我都有点好笑。其实他们盘弄我的总价,最多两万块钱。 为检验本文算法的性能,在同一台计算机的MatlabR2010b环境中,采用如表1中设置的实验参数,结合著名的ZDT1、ZDT2、ZDT3、ZDT4、ZDT6[17]这5个测试函数对本文算法独立运行30次进行测试,ZDT问题于2000年由Zitzler,Deb以及Thiele提出,其中ZDT1、ZDT2、ZDT3比较简单。ZDT4与ZDT6的求解难度大,因为在ZDT4的搜索空间中,一共有219个不同的局部最优前沿;ZDT6问题的Pareto前沿上的最优解分布不均匀,且越接近Pareto前沿其解分布越不均匀。对ZDT1、ZDT2、ZDT3、ZDT4、ZDT6函数的求解,能有效检验算法的性能。将实验结果与NSGA-II算法[3]、DEPEA算法[16]进行对比并根据实验结果分析算法性能。NSGA-II算法采用基于种群个体分级快速非支配排序方法和拥挤距离比较算子提高算法进化性能;DEPEA算法采用基于子种群分级的方式结合多种算子推动算法进化。 表1 实验参数设置 5.2 评价指标 采用以下指标[3]来评价算法的优劣:(1)时间测度T(相同评价次数下算法所用的时间);(2)收性测度M1;(3)分布性测度SD;(4)覆盖指标C,并画出Pareto前沿的图形进行比较。 5.3 实验结果与分析 表2和表3给出了5个标准测试函数独立运行30次以下本文算法和NSGA-II算法(1)T、(2)M1、(3)SD、(4)C指标的平均值。表4给出了5个标准测试函数独立运行30次以下本文算法和DEPEA(1)M1(2)SD指标的平均值。图3(a)、(b)、(c)、(d)及(e)给出本文算法算法对5个标准测试函数的优化结果与它们的真实Pareto前沿。 如表2和表3所示,本文算法在测试函数ZDT1、ZDT2、ZDT3、ZDT4及ZDT6上的测试结果T、M1、SD和C指标的平均值都明显优于NSGA-II。由于本文算法对精英种群的划分是根据非支配解结合网格选择得到两个不同级别的精英种群,不同于NSGA-II基于种群个体分级快速非支配排序确定多个级别的种群的方式,因而本文算法的时间消耗(T)要明显低于NSGA-II。NSGA-II只有单一的模拟二进制交叉算子[3],而本文算法采用了多种算子配合推进算法进化,尤其当个体较为接近时,配合使用翻转交叉算子FCO,能够将某些维上好的结果迅速地传到其他维上,因而算法不易陷入局部最优,收敛性较好(M1)。为保证种群多样性,本文算法划分多个子种群,每个子种群建立概率模型并根据精英个体的浓度独立的进化,保证种群多样性,因而算法有较好的分布性(SD)。 表2 本文算法在T、M1、SD和C测度上的比较 表3 NSGA-II在T、M1、SD和C测度上的比较 如表4所示,本文算法在测试函数ZDT4、ZDT6这2个标准测试函数上面实验结果明显都优于DEPEA算法。ZDT4、ZDT6问题求解的难度较大,本文算法能够搜索出ZDT4函数219个其中的唯一的全局的Pareto最优前沿,说明该算法有较好的全局搜索能力,与DEPEA算法相比,由于采用了基于子种群进化的方式,在进化的同时有考虑精英个体的浓度,因而有效的保证种群的多样性,避免陷入局部最优,所以保证了收敛性(M1)和分布性(SD)。本文算法求解ZDT6问题时最终得到的解都是收敛的,未出现不收敛的解,由于在划分两个精英种群时采用了网格选择,可以更好地选择出高级别的精英个体。结合三种交叉算子能够更好地对不同级别的精英个体进行进化操作,推进算法持续进化,避免陷入局部最优,保证算法的勘探和探索能力。 表4 本文算法、DEPEA在CM、SD测度上的比较 图3 五种测试函数的优化结果 本文在分布估计算法的基础上引入精英协同进化和多种群独立进化思想,提出了一种基于精英协同的多种群分布估计算法本文算法。该算法采用精英协同策略将精英个体分成不同级别的种群,对不同级别的精英个体采用不同的进化操作,可避免算法陷入局部最优。它的多种群独立进化方式能将整个种群分成若干个子种群,各个子种群独立进化,解决传统EDA个体随进化代数增加逐步接近,种群多样性差的问题,避免陷入早熟收敛。通过以上策略保证算法的探查和探究能力,结合实验结果分析可见:该算法与NSGA-II算法、DEPEA算法相比,Pareto最优解收敛更快,分布更加均匀。 [1] 公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报,2009,20(2):271-289. [2] Horn J,Nafpliotis N,Goldberg D E.A Niched Pareto Genetic Algorithm for Multi-objective Optimization[C]//Proceedings of the lst IEEE Conference on Evolutionary Computation.Piscataway:IEEE Press,1994:82-87. [3] Deb K,Pratap A,Agaiwal S,et al.A Fast and Elitist Multi-objective Genetic Algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197. [4] Coello C A C,Lechuga M S.MOPSO:A proposal for multiple objective particle swarm optimization[C]//Proceedings of the 2002 Congress on Evolutionary Computation.IEEE,2002,2:1051-1056. [5] Zhang Q,Zhou A,Jin Y.RM-MEDA:A regularity model-based multiobjective estimation of distribution algorithm[J].IEEE Transactions on Evolutionary Computation,2008,12(1):41-63. [6] Gong M,Jiao L,Du H,et al.Multiobjective immune algorithm with nondominated neighbor-based selection[J].Evolutionary Computation,2008,16(2):225-255. [7] 程玉虎,王雪松,郝名林.一种多样性保持的分布估计算法[J].电子学报,2010,38(3):591-597. [8] Madera J,Alba E,Ochoa A.A parallel island model for estimation of distribution algorithms[M].Towards a New Evolutionary Computation.Springer,2006:159-186. [9] Hastie T,Stuetzle W.Principal curves[J].Journal of the American Statistical Association,1989,84(406):502-516. [10] Liu H,Li X.The multiobjective evolutionary algorithm based on determined weight and sub-regional search[C]//IEEE Congress on Evolutionary Computation.IEEE,2009:1928-1934. [11] 刘全,王晓燕,傅启明,等.双精英协同进化遗传算法[J].软件学报,2012,23(4):765-775. [12] Zhou S,Sun Z.A survey on estimation of distribution algorithms[J].Acta Automatica Sinica,2007,33(2):113-124. [13] Deb K,Mohan M,Mishra S.Towards a quick computation of well-spread pareto-optimal solutions[C]//Proceedings of the 2nd International Conference on Evolutionary Multi-criterion Optimization.Springer,2003:222-236. [14] Potter M A,Jong K A D.A cooperative coevolutionary approach to function optimization[C]//The Third Conference on Parallel Problem Solving from Nature (PPSN III).London:Springer,1994:249-257. [15] 慕彩红,焦李成,刘逸.M-精英协同进化数值优化算法[J].软件学报,2009,20(11):2925-2938. [16] 周丹,耿焕同,贾婷婷,等.一种基于双精英种群的协同进化算法研究[J].计算机应用与软件,2015,32(2):244-248,271. [17] Zitzler E,Deb K,Thiele L.Comparison of multiobjective evolutionary algorithms: Empirical results[J].Evolutionary Computation,2000,8(2):173-195. [18] 耿焕同,朱海峰,张茜,等.均衡分布性与收敛性的协同进化多目标优化算法[J].控制与决策,2013,28(1):55-60. MULTI-POPULATION ESTIMATION OF DISTRIBUTION ALGORITHM BASED ON ELITE COOPERATION Zhou Dan Xie Min Liu Fang Wei Jian (DepartmentofComputerEngineering,TongdaCollege,NanjingUniversityofPostsandTelecommunications,Yangzhou225127,Jiangsu,China) Aiming at the problem of weak ability of local search and falling into premature convergence easily which exist in the traditional estimation of distribution algorithm(EDA), a new algorithm based on the distributed estimation algorithm is proposed to solve the problems. In this algorithm,the elite strategy is introduced and the method of dividing the sub populations is adopted. The algorithm combines two types of reproducing strategies,one is using the elite cooperative operation for local search the evolution process and developing new searching areas, the other is dividing population into sub ones to ensure the diversity by independent evolution. Experimental results of benchmark test functions show that the algorithm has obvious advantages in both convergence and diversity. Estimation of distribution algorithm Premature convergence Elite cooperation Sub population 2015-11-26。周丹,助教,主研领域:智能计算。谢敏,助教。刘方,助教。韦剑,助教。 TP183 A 10.3969/j.issn.1000-386x.2017.01.0514 基于双精英协同的多种群分布估计算法
5 仿真实验




6 结 语

