一种求解混合零空闲置换流水车间调度禁忌分布估计算法

张晓霞 吕云虹

(辽宁科技大学软件学院 辽宁 鞍山 114051)

一种求解混合零空闲置换流水车间调度禁忌分布估计算法

张晓霞 吕云虹

(辽宁科技大学软件学院 辽宁 鞍山 114051)

结合混合零空闲置换流水车间调度问题MNPFSP(Mixed no-idle permutation flowshop scheduling problem)的特性，运用基于概率模型的分布估计算法解决该问题。算法将启发式算法融入分布估计算法中提高了初始解的质量。为了避免算法陷入局部最优，将禁忌算法融入分布估计算法中，提出一种禁忌分布估计算法求解混合零空闲置换流水车间问题。为了提高种群的多样性，加入了三种邻域搜索。实例测试结果显示，该算法求解混合零空闲置换流水车间问题具有很好的优势。

混合零空闲置换流水车间调度问题算法 分布估计算法 启发式算法 禁忌算法

0 引 言

置换流水车间调度问题属于经典的调度问题，它是在流水车间调度问题约束的基础上，进一步增加所有工件在任一台机器上的加工顺序均相同的约束后形成的生产调度问题[1]。零空闲置换流水车间调度问题NPFSP(No-idle permutation flowshop scheduling problem)是在置换流水车间调度问题的前提下，设置一台机器一旦开始加工就不能中断，直到加工完所有的工件。当前关于NPFSP的研究，在实际生产过程中，NPFSP是很少存在的，更多的是混合零空闲调度问题，因此研究混合零空闲置换流水车间调度问题MNPFSP具有十分重要的意义。

MNPFSP是典型NP难题。对于问题规模较小的MNPFSP，可以采用精确算法来求得问题的解，例如启发式算法等。但在解决实际问题的情况下，MNPFSP问题规模相对较大，问题相对复杂，此时不适合用精确算法求解该问题。智能优化算法作为一种经常求解NP问题的方法，人们对于求解大规模生产调度问题更多地采用智能优化算法。当前用于解决生产调度问题的算法有遗传算法[2]、蚁群算法[3]、分布估计算法[4]和人工蜂群算法[5]等。

分布估计算法EDA(Estimation of distribution algorithm)兴起成为最近几年里研究的热点问题，它的思想来源于遗产算法。在遗产算法的基础上，EDA采用概率分布模型来替换遗传算法中的交叉和变异等操作，并根据概率模型的信息，运用各种策略对种群进行采样，产生新种群，通过反复地进化得到最终结果。概率分布模型很好地克服了遗传算法构造模块破坏的问题。这种算法具有很强的自适应能力和自学习能力，不依赖问题的具体领域[6]。根据概率模型的复杂度，分布估计算法大致分为三类：变量无关、双变量相关和多变量相关[7]。

EDA引起在各个领域的专家学者广泛的研究，并取得了不错的进展。例如巡航导弹航迹规划中的应用[8]、旅行商问题的应用、图像处理和过程控制等。本文将分布估计算法应用于求解混合零空闲置换流水车间调度问题，结合问题的特点，将启发式算法与禁忌算法融入到算法中，来提高算法的搜索效率。为了防止算法陷入局部最优的状况，在算法中加入局部搜索策略。通过实例验证了本文的混合分布估计算法在求解该问题上有很大的优势。

1 MNPFSP问题的描述

混合零空闲置换流水车间调度问题就是NPFSP与PFSP调度的混合，主要是指在加工过程中，存在某些机器一旦开始加工就不能停止，直到加工结束，而其余的机器在加工过程中是可以停止的。

MNPFSP的数学描述如下：Π(π1，π2，…，πk，…，πn)是工件加工的一个调度。其中下标表示在加工序列中的位置。用l表示工件在加工序列的位置，Ci,[l]表示l位置上的工件在机器i上的加工完成时间，用Si,[l]表示l位置上的工件在机器i上开始加工时间。用Pi,j表示工件j在机器i上加工所消耗时间。用ai表示位置1的工件要在开始加工时延迟加工时间，为了便于描述，公式中把推延时间放在后面出现延迟的地方，最终结果是相同的。将NPFSP的机器集合记为M1，空闲的记为M。这里将最大完成时间makespan设为调度指标。其公式为[9]：

(1)

(2)

(3)

(4)

Cmax(π)=Cm,[n]

(6)

式(1)计算了位置1的工件在第一个机器的起始与终止时间。式(2)是计算位置1的工件在各个机器上的起始与终止时间。式(3)是计算不同位置的工件在机器1上的起始与终止时间。式(4)是计算不同位置上的工件在机器2上的起始与终止时间。式(5)是计算不同位置的工件在剩余机器上的起止时间。式(6)是调度的目标函数。

2 分布估计算法

分布估计算法这一概念最初是在1996年被提出，近年来国际上进化计算领域的各大学术会议(如ACM SIGEVO、IEEE CEC等)都将分布估计算法作为重要专题予以讨论[7]，并成功解决了一些实际的问题。分布估计算法运用概率模型来替换遗传算法中的交叉、变异操作，根据概率模型产生新一代的种群。基本步骤如下：

(1) 产生初始化种群。

(2) 计算个体的适应值，选择群体中的优势群体。

(3) 根据优势群体的信息，建立概率模型，来产生下一代。

(4) 根据优势群体的概率模型，采用一定的策略来产生新个体并进行更新操作。

(5) 重复以上步骤，如果满足终止条件，则算法停止；否则，转步骤(2)继续执行。

3 改进的分布估计算法求解MNPFSP

为了提高算法的收敛速度，在初始化种群的过程中，引入了NEH启发式算法，提高初始种群的质量。为了提高算法的局部搜索能力，将2-opt、逆序、交换等操作融入到算法中。同时算法将禁忌搜索算法加入到分布估计算法中，提高算法的全局搜索能力。实验表明这些操作对算法的效率和性能具有很大的提升，能够有效地取得算法较好的解。

3.1 产生初始种群

对于混合零空闲置换流水车间调度问题，直接使用十进制数来编码。用自然数来表示工件的加工顺序，即每个自然数代表一个工件。随机产生T条加工顺序作为初始种群。为了保证种群的多样化和提高收敛速度，这里运用NEH启发式算法对初始种群进行优化，使其产生一个局部最优解，将其放入到初始种群中。

NEH启发式算法是1983年Nawaz、Enscore和Ham共同提出来的[10]。该算法是求解加工时间周期性能最好的。其具体的操作：

(1) 计算工件i在各个机器上的总的加工时间；

(2) 根据工件总的加工时间，非递增的顺序排列N个工件；

(3) 取位于顺序的前两个工件，使部分最大流程时间达到极小；

(4) 令k=3到N，把第k个工件插入到k个可能的位置，求得子调度最优。为了提高种群的质量，剩下的随机产生。

3.2 计算适应值选择优势群体

按照各个工件i在机器上的排列作为加工顺序，所有工件加工完成所使用的时间作为适应度值。时间越长，适应度值越小，反之亦然。按照适应度值将工件进行排序。从适应值较高的种群中选择m个个体作为优势群体。

3.3 建立概率模型

在分布估计算法中，概率模型的构造方式多种多样。本文采用位置概率和连接概率相结合的方式来建立概率模型，即建立两个概率模型。根据种群中的优势群体两两连接出现的工件频率来建立一个频率矩阵。

(7)

式中，ei,j表示在工件i后面的连接工件是j的频率，如果δ(xl)的值为1，表示加工顺序l中工件i和工件j两两相邻出现，否则为0。

类似建立一个频率矩阵来记录优势种群的位置概率模型。统计计算在各个加工机器上工件出现的频率，即在序列Π(π1，π2，…，πk，…，πn)中πk表示排在k位置上的工件号。

在构建概率矩阵时，采用了文献[11]的概率矩阵优化方法，将PBIL[7]算法的Heb规则运用到概率矩阵构造中，即：

(8)

式中，λ∈(0,1)，λ越大，对下一代的影响也就越大，反之越小。

3.4 禁忌算法产生新种群

为了产生新一代种群，防止算法早熟，本文将禁忌算法融入到EDA算法中，提出了一种禁忌思想的改进分布估计算法。禁忌算法对搜索过的区域进行封锁避免迂回搜索，同时赦免禁忌区域中一些优良状态，进而保证搜索的多样性，防止陷入局部最优[12]。利用禁忌算法的特点，首先初始化了长度为K的禁忌列表，然后将要进化的优势群体赋值给禁忌列表。当最优解在KT代内不再进化时，更新禁忌列表。将该局部最优解个体作为禁忌对象，从而禁止产生相同适应度值的新一代个体。反复抽样，产生新一代群体。

算法利用轮盘赌法根据位置概率的分布产生新个体的第一个工件，为了保持种群的多样性，其余的部分则随机产生第一个工件。剩下的工件利用轮盘赌法根据禁忌算法中的禁忌列表产生。判断种群进化的收敛性，若达到收敛则算法结束，否则更新概率模型，选择新的优势群体继续进化。

3.5 更新概率模型

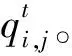
(9)

4 邻域搜索策略

为了算法避免陷入局部最优，增强算法的局部搜索效率。在算法中加入了2-opt操作、逆序操作[13]和交换操作[13]。

2-opt邻域搜索算法是一种简单的启发式邻域搜索算法[12]。其基本思想是：对一条有向路径，选择两条不相邻边，如(x1，x2)和(x3，x4)；将这两条边断开，以某种方式连接成新有向路径，如有向路径的边变成(x1，x3)和(x2，x4)；使新的路径长度满足约束并小于原来的路径长度，如C(x1，x2)+C(x3，x4)>C(x1，x3)+C(x2，x4)，新的路径作为当前路径。由于2-opt操作是从第一个工件开始搜索遍历的，而生产调度的问题跟它有所不同，第一个工件和最后一个工件不参与2-opt操作，所以将2-opt操作用于每一代的优势群体。

逆序操作在工件排列的顺序中随机选定两个位置x和y，将选定的两个位置中间的工件顺序逆序排列。即工件顺序为(2，5，3，4，1，6，7)，选定的点为x=2，y=6，则工件的排列顺序为(2，6，1，4，3，5，7)。

为了提高种群的多样性，在算法中还添加了交换操作。交换操作与逆序操作不同，即在工件序列中随机选定两个位置x和y，但是对这两个选定的位置进行交换。即设工件序列(2，5，3，4，1，6，7)，选定的点为x=2，y=6，则工件的排列顺序为(2，6，3，4，1，5，7)。

5 仿真实验

由于研究MNPFSP方面的问题非常少，目前没有经典的测试实例，本文运用测试NPFSP问题的实例来测试MNPFSP问题，并将NPFSP问题的最优解作为MNPFSP问题的最优解。采用了Taillard提出的120个经典Benchmark问题进行测试，为了证明数据的有效性，每个问题测试5次。该算法的仿真环境为：处理器为2.27 GHz,内存为2 GB，32位操作系统，系统为Windows 7，编译环境为Visual Studio 2010。本文在求得最优解或运行到最大代数时，程序结束运行。本文算法的设置参数为：种群规模Scale=100，学习效率AF=0.5，优势群体的规模为T=30，禁忌表长度L=10，最大运行代数5000，最小限定值为0.00001×α/n，最大限定值为0.0001×α/n。

针对MNPFSP的特性将每个测试实例分为7种问题进行测试：

(1) 前50%的机器是NIPFSP，后50%的机器是PFSP：FRTST50。

(2) 后50%机器是NIPFSP，前50%的机器是PFSP：SECOND50。

(3) 空闲与零空闲机器交替出现：ALTERNATE。

(4) 有25%的机器是NIPFSP的并且是随机指定的：RANDOM25。

(5) 有50%的机器是NIPFSP的并且是随机指定的：RANDOM50。

(6) 有75%的机器是NIPFSP的并且是随机指定的：RANDOM75。

(7) 全部是零空闲机器：ALL。

七种情况的的测试结果如表1和表2所示。

表1 前三种情况的测试结果

表2 后四种情况的测试结果

表中PRD表示平均相对百分比偏差，即算法的最优解的平均相差百分比。SD表示平均标准差，即所求解的平均偏离程度，体现算法的稳定性[2]。从表1和表2中可以看出，任意混合零空闲置换流水车间调度的PRD都小于全部是零空闲置换流水车间的调度，并且随着种群规模的不断增加，MNPFSP问题中的PRD明显优于NPFSP问题。虽然MNPFST测试实例中的SD不小于NPFST调度，但是基本接近于零空闲调度。所以混合零空闲置换流水车间问题运用本文算法解决具有良好的优越性和全局搜索能力。

因为MNPFSP问题是相对复杂的车间调度问题，目前关于混合零空闲置换流水车间问题的研究非常少，在Benchmark问题中MNPFSP问题的最优解目前尚未求得。为了更好地验证本文算法对解决流水车间问题的优良性，将禁忌分布估计算法(TEDA)的第七组测试数据，即解决零空闲置换流水车间问题，与遗传算法(GA)[14]、离散粒子群算法(DPSO)[14]和离散蛙跳算法(DSFLA)[15]，进行解决NPFSP问题的比较。文中的参数数据来自相应文献，四种算法的对比结果如表3所示。

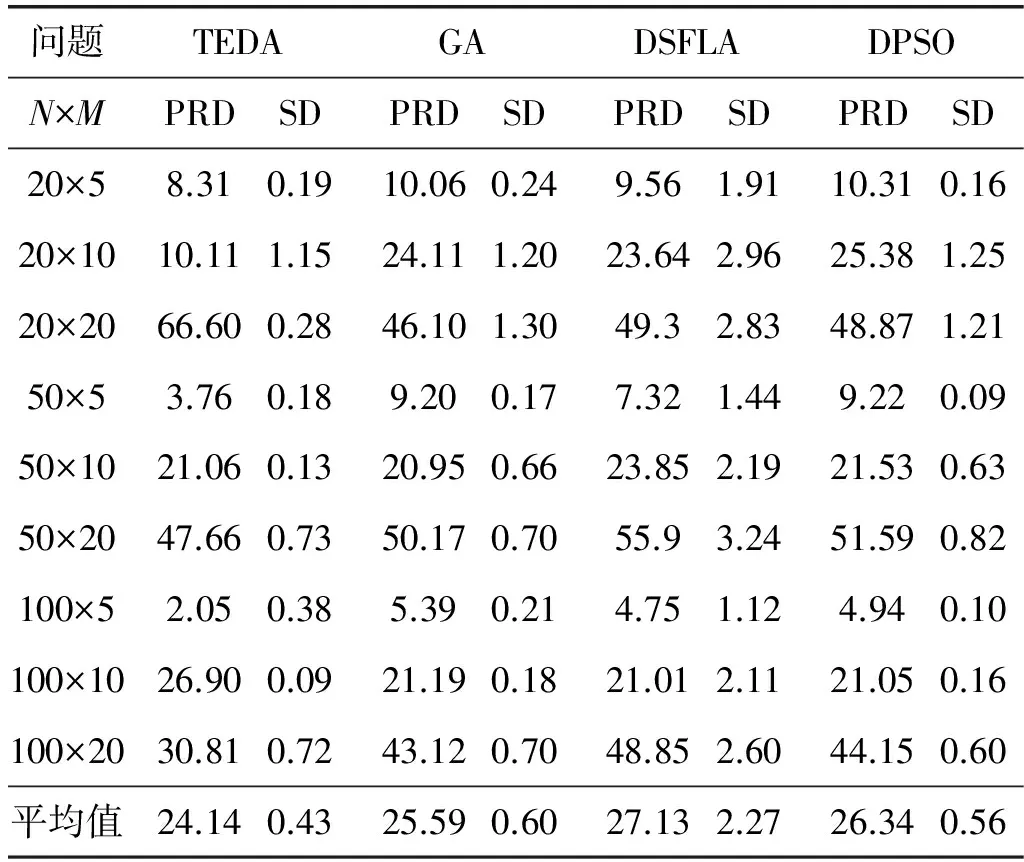
表3 四种算法的对比结果

表3中测试实例数据中，本文算法除了20×20和100×10中PRD的数据稍大于其他算法，剩下的PRD数据都小于其他算法，并且TEDA的PRD平均值优于其他算法，因此可以验证TEDA具有更好寻优搜索能力和全局搜索能力。TEDA算法的平均标准差都小于其他算法，表明该算法具有很好的稳定性。

为了更好地体现算法的性能，将TEDA算法与DPSO算法进行算法最优解平均标准差的折线图比较，如图1所示。

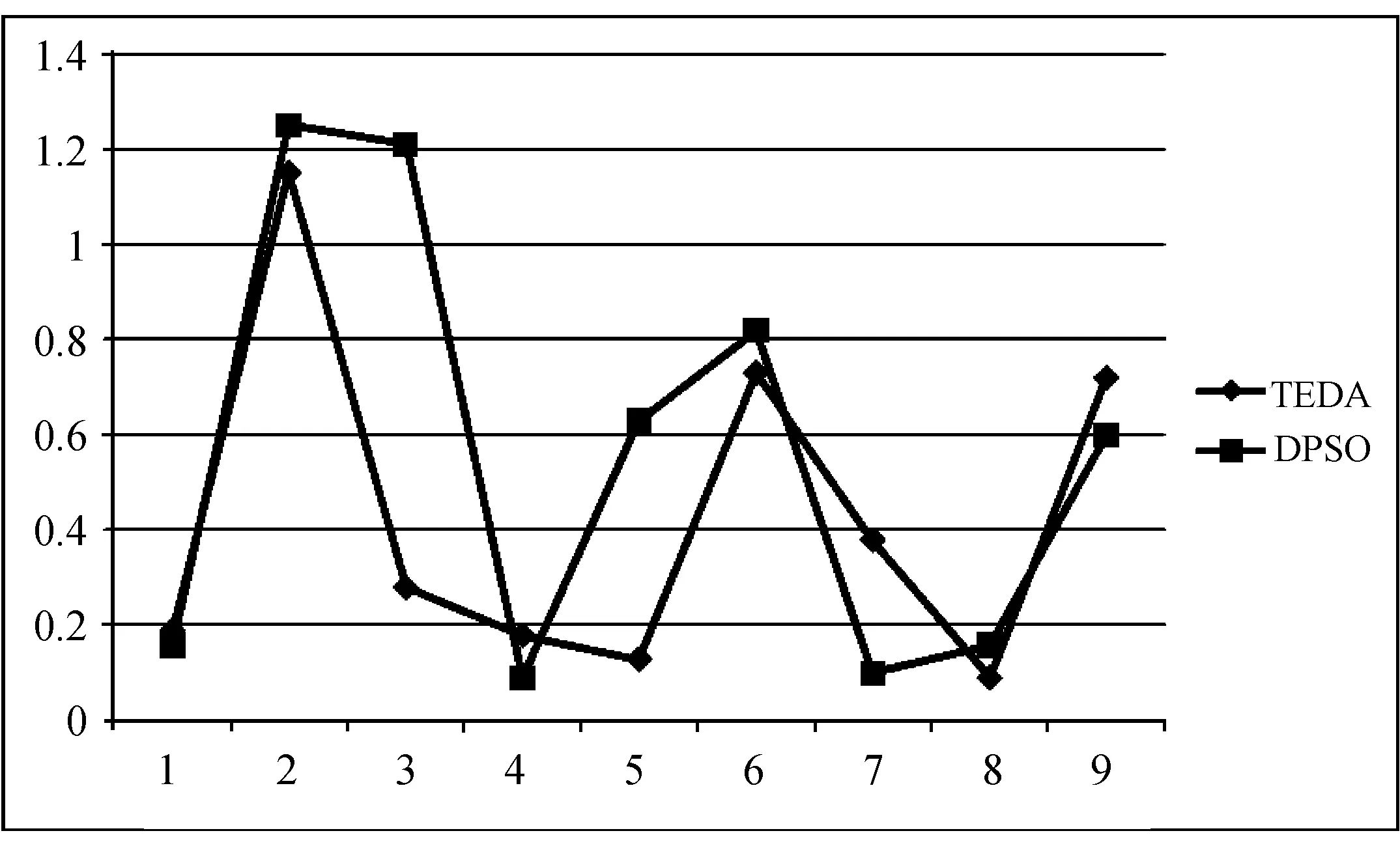
图1 TEDA算法与DPSO算法的SD比较折线图

根据表3中SD的数据，画出TEDA算法与DPSO算法的最优解平均标准差折线图，横坐标表示问题N×M，其中点1就代表规模20×5，纵坐标表示SD。从图1中可以看出，除了在规模50×5、100×5和100×20，即点4、点7和点9的位置，TEDA算法的SD小于DPSO算法，而且TEDA算法SD的平均值明显低于DPSO算法。这表明TEDA算法在解决混合零空闲置换流水车间问题时表现出很好的稳定性。

为了更好地说明算法的收敛性，图2给出了TEDA算法求解中规模50×5问题的收敛曲线图。由图可见，TEDA具有较快的收敛性。

图2 TEDA算法的收敛曲线

6 结 语

本文根据分布估计算法与禁忌算法各自的特点，提出了一种融合了禁忌算法的混合分布估计算法求解MNPFSP问题。算法将禁忌算法与分布估计算法融合在一起，通过引入禁忌列表来控制种群的进化方向，有效避免了算法陷入局部最优的陷阱。为了提高算法的收敛速度，引入三种局部搜索策略；同时引入了NEH算法，提高了初始种群的质量。通过仿真测试表明，本文提出的混合分布估计算法在求解MNPFSP问题时具有一定的优越性。但是MNPFSP问题是一个非常新颖的问题，目前关于此类问题的研究十分少，本文中用于测试的实例的最优解目前尚未求得，因此本文算法用于求解MNPFSP的优越性还需进一步的研究。

[1] 刘长平，叶春明.求解置换流水车间调度问题的布谷鸟算法[J].上海理工大学学报，2013,35(1)：17-20.

[2] 郭海东.遗传算法及其在生产调度中的应用研究[D].浙江：浙江工业大学,2004.

[3] 张丽萍.改进的蚁群算法求解置换流水车间调度问题[J].微型机与应用,2014,33(12):66-68，72.

[4] Quan Ke Pan,Rubén Ruiz.An estimation of distribution algorithm for lot-streaming flow shop problems with setup times[J].OMEGA,The International Journal of Management Science，2012，40(2):166-180.

[5] M Fatih Tasgetirena,Quan Ke Pan,P N Suganthan,et al.A discrete artificial bee colony algorithm for the no-idle permutation flowshop scheduling problem with the total tardiness criterion[J].Applied Mathematical Modelling,2013,37(10/11):6758-6779.

[6] 张凤超.改进的分布估计算法求解混合流水车间调度问题研究[J].软件导刊,2014,13(8):23-26.

[7] 周树德，孙增圻.分布估计算法综述[J].自动化学报,2007，33(2)：113-124.

[8] 吴红，王维平，王磊，等.分布估计算法在巡航导弹航迹规划中的应用[J].电光与控制,2010,17(7):6-10.

[9] Quan Ke Pan,Rubén Ruiz.An effective iterated greedy algorithm for the mixed no-idle permutation flowshop scheduling problem[J].OMEGA,The International Journal of Management Science,2014,44: 41-50.

[10] 韦有双，杨湘龙，冯允成.一种新的求解Flow Shop问题的启发式算法[J].系统工程理论与实践,2000,20(9)：41-47.

[11] 何小娟，曾建潮.基于优良模式连接的分布估计算法求解TSP问题[J].模式识别与人工智能,2011，24(2):185-193.

[12] 汪定伟，王俊伟，王洪峰，等.智能优化方法[M].北京：高等教育出版社,2007.

[13] 刘长平，叶春明.求解零空闲置换流水车间调度问题的离散萤火虫算法[J].系统管理学报,2014,23(5)：723-727.

[14] 潘全科，王凌，赵保华.解决零空闲流水线调度问题的离散粒子群算法[J].控制与决策，2008,23(2):191-194.

[15] 王亚敏，冀俊忠，潘全科.基于离散蛙跳算法的零空闲流水线调度问题的求解[J].北京工业大学学报，2010,36(1):124-130.

A TABU ESTIMATION OF DISTRIBUTION ALGORITHM TO SOLVE THE MIXED NO-IDLE PERMUTATION FLOWSHOP SCHEDULING PROBLEM

Zhang Xiaoxia Lü Yunhong

(SchoolofSoftware,UniversityofScienceandTechnologyLiaoning,Anshan114051,Liaoning,China)

According to the characteristics of the mixed no-idle permutation flowshop scheduling problem,an estimation of distribution algorithm based on probability model is used to solve this problem.What’s more,the heuristic algorithm is designed into the estimation of distribution algorithm in order to improve the quality of the initial solution.In order to avoid the algorithm into local optimum,the tabu algorithm is designed into the estimation of distribution algorithm.The tabu estimation of distribution algorithm is proposed to solve the mixed no-idle permutation flowshop scheduling problem with three added kinds of local searches in order to improve the diversity of population.Experimental result shows that the algorithm has advantages to solve this problem.

Mixed no-idle permutation flowshop scheduling problem Estimation of distribution algorithm Heuristic algorithm Tabu algorithm

2015-09-03。辽宁省教育厅科学研究项目(L2015265)。张晓霞，教授，主研领域：智能优化算法，组合优化问题。吕云虹，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2017.01.049