基于相关拓扑势的社团发现算法

赵文涛 赵好好 孟令军

1(河南理工大学计算机科学与技术学院 河南 焦作 454000)2(河南省普通高等学校矿山信息化研究重点实验室 河南 焦作 454000)

基于相关拓扑势的社团发现算法

赵文涛1,2赵好好1孟令军1

1(河南理工大学计算机科学与技术学院 河南 焦作 454000)2(河南省普通高等学校矿山信息化研究重点实验室 河南 焦作 454000)

针对传统算法社团划分精度较低以及模块度函数分辨率低的问题，提出一种基于相关拓扑势的社团发现算法，简称BITP算法。该算法考虑节点的相关性因素，引入相关拓扑势来衡量节点的影响力，寻找出其中的极大势值点，采用标签传播的思想对社团的规模进行控制。在人工合成网络和真实网络上，与多种算法进行实验对比，结果表明该算法多次运行结果相对稳定且社团划分精度较高。算法时间复杂度为O(n)，且不需要先验知识，更适合大规模复杂网络上的社团结构挖掘。

社团结构 复杂网络 相关拓扑势 标签传播

0 引 言

复杂网络的结构特性是现实系统中个体之间复杂关系的真实表现。大量实证研究结果表明，真实网络结构不仅普遍具有小世界和无标度等特性，而且呈现出明显的社团结构[1-3]。社团结构是指网络中的节点根据某种共同属性，子集合内部节点之间的连接相对紧凑，子集合之间节点之间的连接相对稀疏[2]。

Girvan和Newman最先提出了基于边界数的社团发现算法，称为GN算法[1]，但算法效率和社团划分精度较低。随后，Newman等人又引入模块度函数[3]来对社团划分质量进行评价。之后，人们采用多种方法来对模块度进行优化以达到更好的社团划分效果，例如FASTGREEDY算法[4]、MULTILEVEL算法[5]等。然而近期研究表明，模块度定义存在分辨率的限制，不适合划分社团规模大小不一的网络结构。而真实网络结构通常存在异质性，社团大小不均匀，模块度优化方法很难保证社团结构挖掘的准确性。另外，其他一些快速算法虽然效率很高，却是以损失精度为代价，诸如LPA算法[6]、WALKTRAP算法[7]、LEC算法[8]、SPINGLASS算法[9]、INFOMAP算法[10]等。

鉴于模块度定义存在的缺陷，为了有效揭示网络内在的社团结构，淦文燕等[11]提出了一种基于拓扑势的网络社团发现算法，将数据场中拓扑势的概念引入至社团发现。随后，张健沛[12]、石立新[13]、张桂杰[14]等人基于拓扑势并结合其他方法进行相关算法的优化，验证其各自算法的有效性。

这些基于拓扑势的社团发现算法均是基于传统拓扑势函数，本文提出了一种基于相关拓扑势的社团发现算法(简称BITP算法)。在传统拓扑势的基础上，结合节点之间的相关性定义，引入相关拓扑势的概念。该方法不需要先验知识，通过相关拓扑势来衡量网络中节点的影响力，采用标签传播的方法进行社团结构的挖掘，算法相对稳定，社团划分精度较高。

1 相关概念

1.1 相关性

文献[15]中相关性定义了无向无权网络中用于衡量节点之间关系的紧密度，具体定义如下：

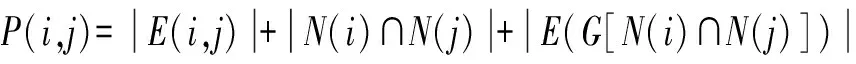
(1)

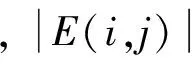
1.2 拓扑势

物理学中用场来描述物质粒子间的相互作用。物理场是其中的一种，用来描述拓扑场的标量势函数。势场分为长程场和短程场。在长程场中，势值的大小与距离成反比，在距离场源很远的地方仍然存在着场力的作用(如重力势场和静电势场)。而在短程场中，中心势场的势值会随着距离的增大而急剧下降，相应的场力也会很快衰减至零。受物理场思想的启发，诸多研究倾向于采用代表短程场且具有良好数学性质的高斯势函数描述节点间的相互作用。

给定网络G=(V,E)，其中，V={1,2,…,n}为节点的非空有限集。根据拓扑势场中势函数定义[16]，任意节点i∈V的拓扑势可表示为：

(2)

其中，dij表示节点i与j之间的最短路径长度；影响因子σ用于控制每个节点的影响范围；mi表示节点i(i=1,2,…,n)的固有属性(如质量等)。

传统的拓扑势计算[11-14]中将每个节点视为均质的，拓扑势TP(TopologicalPotential)计算式可表达为：

(3)

1.3 相关拓扑势

节点的相关性从网络拓扑结构的角度出发，充分考虑节点之间连边的数目对节点之间关系的影响。给定网络，节点之间的相关性是固定的、不可改变的，故可以将其视为网络中节点的固有属性。

式(3)中传统的拓扑势计算方法忽略了节点固有属性对节点拓扑势的影响作用，而实际复杂网络中不同节点对单个节点影响程度不同，即相关程度不同。故本文考虑节点之间的相关性，提出节点的相关拓扑势函数，表示方式如下：

(4)

其中，P(i,j)为节点相关矩阵P中第i行第j列的元素值，即节点i与节点j的相关性。

势函数中影响因子σ用来控制节点的影响力跳数，节点的影响力跳数定义为：

(5)

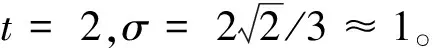
考虑节点的影响力跳数，节点的相关拓扑势ITP(InterrelatedTopologicalPotential)可由式(6)推出：

(6)

在无向无权网络中(以Karate网络为例)，计算所有节点的TP和ITP指标，并画出其分布，如图1和图2所示。网络中节点ITP指标呈局部聚集状态，社团的区分效果要比TP指标更加明显。分别将采用TP指标和ITP指标的社团发现算法简称为BTP算法和BITP算法，后面将对这两种算法作对比分析。

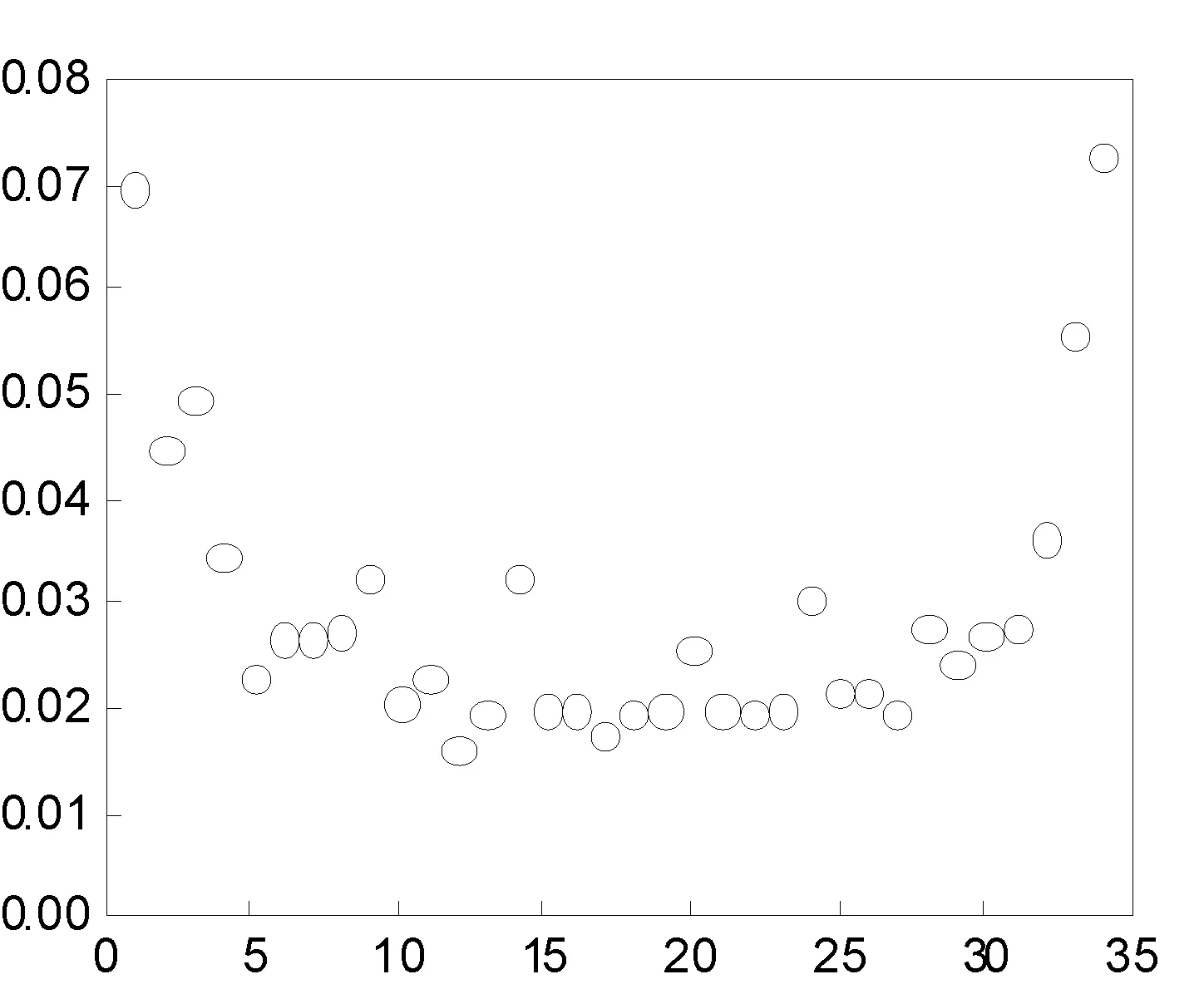
图1 TP指标

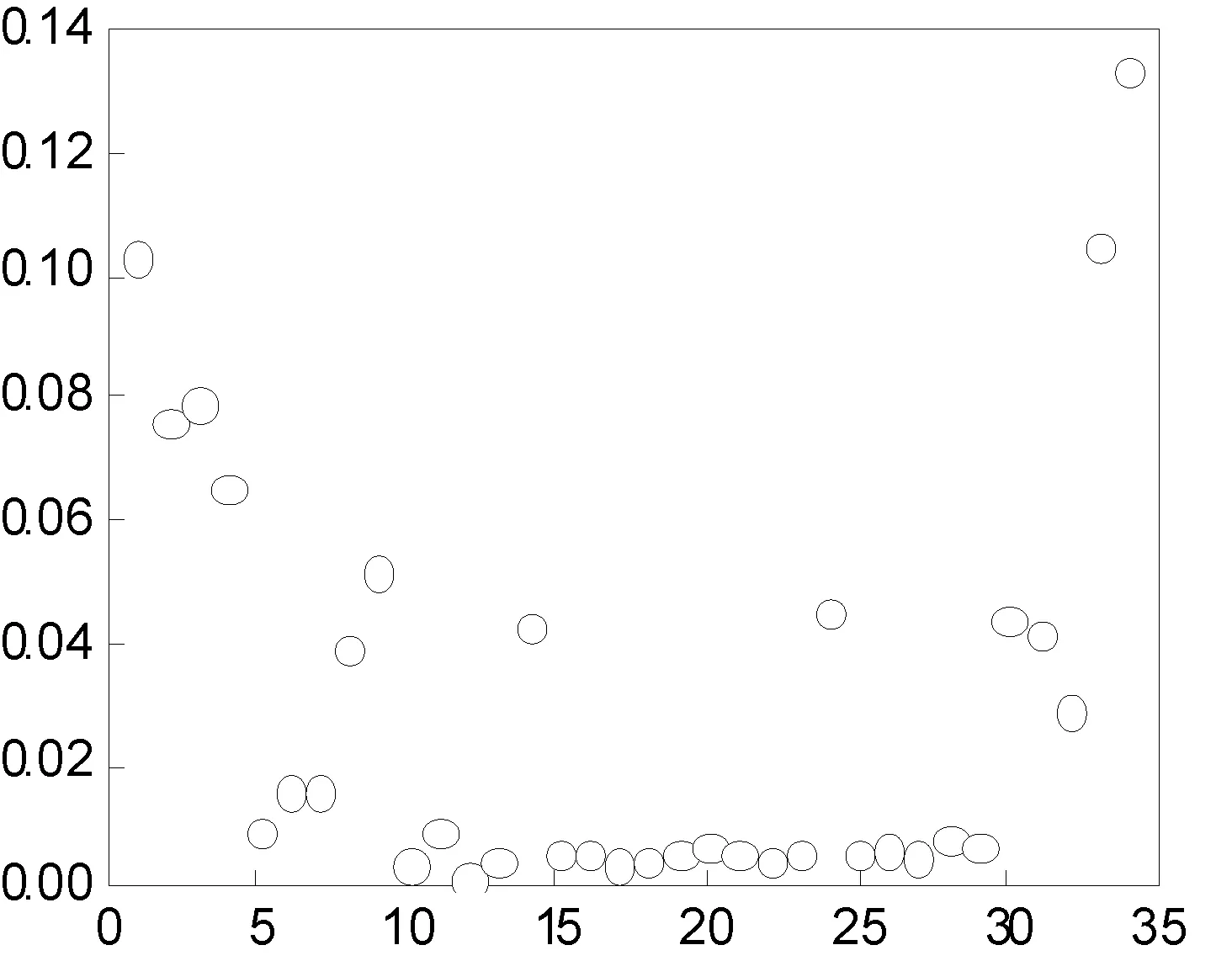
图2 ITP指标

2 算法描述

本文考虑网络中节点之间的相关性，引入节点的相关拓扑势。算法采用贪婪局部搜索的方法搜索网络中的局部极大势值节点，初始化极大值节点的标签为各自的节点标号，然后采用标签传播的方法更新其余节点的标签。

在传统的LPA算法[6]中，节点标签传播规则分为两步：第一步，将节点i的标签更新为其邻居节点中标签数目最多的标签；第二步，若其邻居节点中标签数目最多的标签有多个时，则随机选择其中一个作为节点i的标签。这样的随机操作容易造成算法的不稳定，社团划分结果不够准确。因此，本文的标签传播规则为：

Step1 将节点i的标签更新为其邻居节点中标签数目最多的标签；

Step2 若其邻居节点中标签数目最多的标签有多个时，选择其中相关拓扑势最大的作为节点i的标签。

BITP算法

输入：无向无权网络G=(V,E)，其中，V={1,2,…,n}。

输出：局部社团C={C1,C2,…,Ck}，其中k为局部社团数目。

算法步骤：

(1) 计算所有节点相关拓扑势；

(2) 采用贪婪局部搜索的方法寻找网络中的局部极大势值节点；

(3) 将这些极值点的标签分别初始化为它们各自的节点标号，网络中的其他节点的标签初始化为0。

(4) 按照上述标签传播规则依次对网络中其余节点进行标签更新。

(5) 标签相同的节点同属于同一个局部社团，输出局部社团{C1,C2,…,Ck}。

在BITP算法中，计算节点的相关拓扑势的时间复杂度为O(2n)，n为网络中节点数；贪婪局部搜索极大值的时间复杂度为O(n)，标签更新的时间复杂度为O(n)。本文算法总的时间复杂度为O(2n+n+n)=O(n)。

3 实验评价标准

3.1 模块度指标

模块度[3]用来比较社团划分结果与随机图之间的差异。定义如下：

(7)

其中，m为网络中节点的数目；∑in表示一个社团内部的连边数目；∑tot表示一个社团内部所有节点度的总和。

3.2NMI指标

标准化互信息NMI[17](NormalizedMutualInformation)常用来衡量社团划分结果与真实社团结构之间的相近程度。定义如下：

(8)

其中，A、B分别为两个不同的局部社团所代表的向量；I(A,B)是向量A和向量B的互信息；H(A)是向量A的信息熵；H(B)是向量B的信息熵。NMI的取值为[0,1]，NMI值越大说明社团划分结果与真实社团结构越相似，越小则反之。

3.3VI指标

信息差异VI[18](VariationofInformation)常用来衡量社团划分结果与真实社团结构之间的差异。定义如下：

VI=H(A|B)+H(B|A)

(9)

其中，A、B分别为两个不同的局部社团所代表的向量；H(A|B)是向量A对于向量B的条件熵；H(B|A)是向量B对于向量A的条件熵。VI的取值为[0,log(m)]，m为网络中节点的数目。VI值越小说明社团划分结果与真实社团结构差异越小，越大则反之。

4 实验结果与分析

为了验证BITP算法的准确性与有效性，分别在人工合成网络和真实网络上与多种算法进行实验对比。

4.1 人工合成网络

实验采用LFR(Lancichinetti-Fortunato-Radicchi)[19]基准网络来生成人工合成网络。网络中的节点度和社团大小均符合幂律分布。混合参数μ用来控制局部社团内部连接数与外部连接的比例，取值为[0,1]。其值越小说明内部连接比较紧密，社团结构较强；反之，社团结构较弱。本文仅取其值0.1～0.8。根据μ取值不同对应生成8个不同的人工合成网络，并分别在这些网络上多次运行GN、CNM、LPA、WALKTRAP、LEC、SPINGLASS、INFOMAP、MULTILEVEL、BTP、BITP等十种社团发现算法。人工合成网络具体参数设置分别如表1所示。

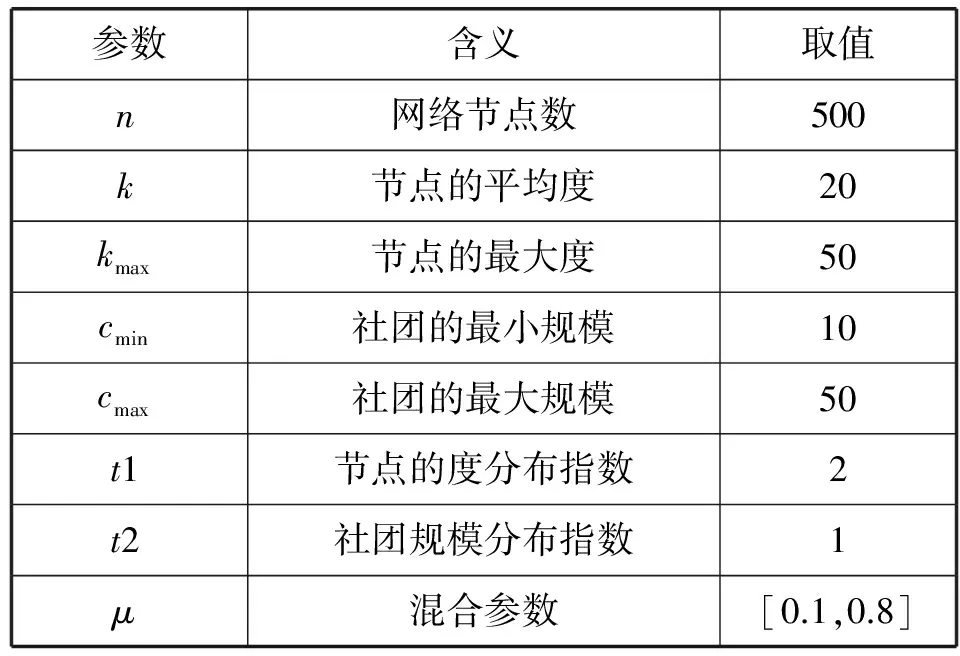
表1 人工网络参数设置

为了比较这些算法社团划分结果与真实网络结构之间差异，分别记录它们划分结果的模块度指标、NMI指标和VI指标，这些指标通过算法运行100次求算术平均值而来。图3反映了十种算法在人工网络上划分结果的各种指标随μ值变化的对比情况。

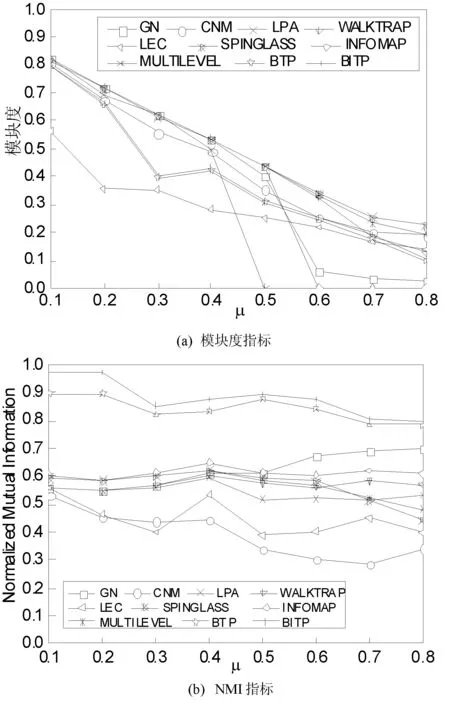
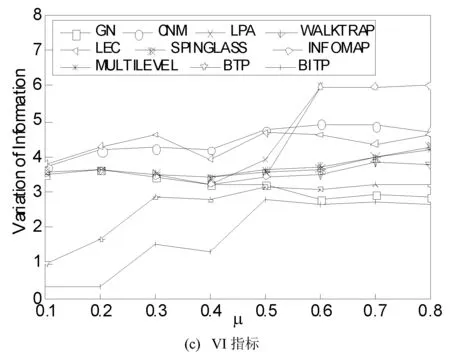
图3 十种算法在500节点网络上各种指标变化曲线图

总体上，各种算法的模块度指标随μ值的增大均有所下降。GN、LPA和INFOMAP三种算法尤为明显，随μ值增大，模块度逐渐趋向于零，说明这些算法运行时不稳定，而其他几种算法相对较稳定。NMI指标和VI指标随μ值的变化，即社团结构的不明显，均呈现出一定程度的波动。基于拓扑势的两种算法BTP和BITP比其他几种算法效果好，与真实网络结构更为相近。与BTP算法相比，BITP算法的NMI指标较高，VI指标较低。这是由于BITP算法考虑到真实网络中节点的相关性信息，划分出来的社团结构要比BTP算法更加合理，与真实网络结构也更为接近，差异也较小。

4.2 真实网络数据集

为了进一步验证本文算法社团划分的效果，在真实网络数据集对其进行测试，以空手道俱乐部网络[20]和宽吻海豚网络[21]为例。

空手道俱乐部网络可表示为G=<34,78>，即网络中节点数为34、边的数目为78。采用BITP算法对其进行社团结构挖掘，首先计算网络中所有节点的相关拓扑势，节点的相关拓扑势分布如图4(a)所示。其中，极大势值为节点1和节点34，分别初始化这两个节点的标签为各自的标号(即标签分别设为1和34)。然后按照上述标签传播规则更新其余节点的标签。最终社团划分结果如图4(b)所示。多次运行BITP算法，与真实网络结构相比，均只有节点3被划分错误，准确率为94.4%，模块度为0.3600。

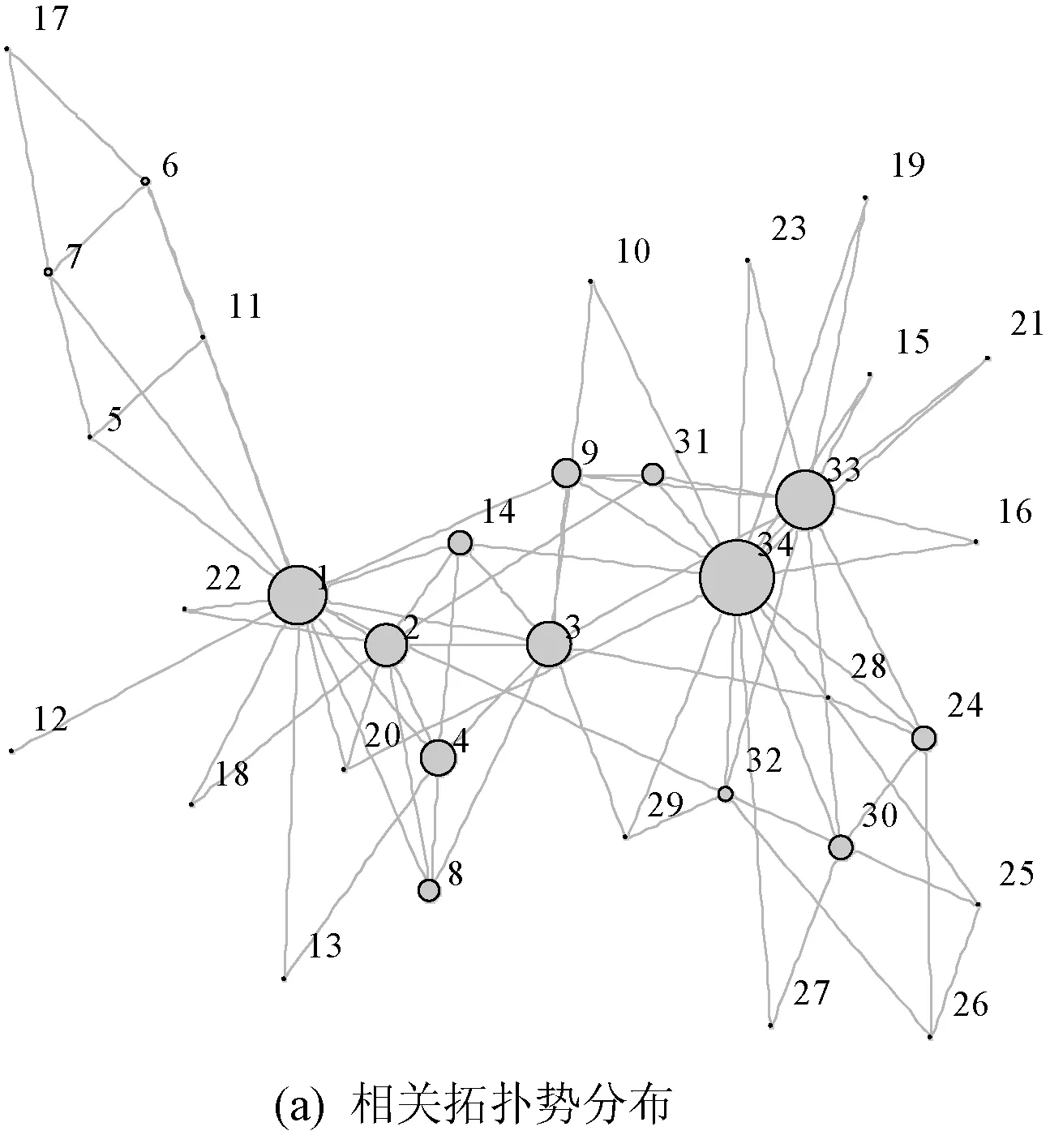
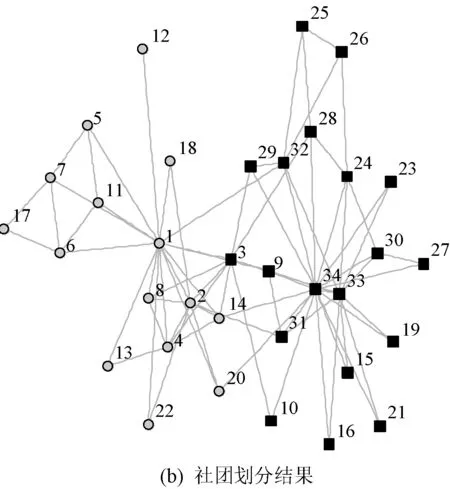
图4 空手道俱乐部网络社团结构

宽吻海豚网络可表示为G=<62,159>，即网络中节点数为62、边的数目为159。节点的相关拓扑势分布如图5(a)所示。极大势值为节点46和节点58，分别初始化这两个节点的标签为46和58。然后按照上述标签传播规则更新其余节点的标签。最终社团划分结果如图5(b)所示。多次运行BITP算法，与真实网络结构相比，均只有节点28和节点40被划分错误，准确率为93.8%，模块度为0.3735。

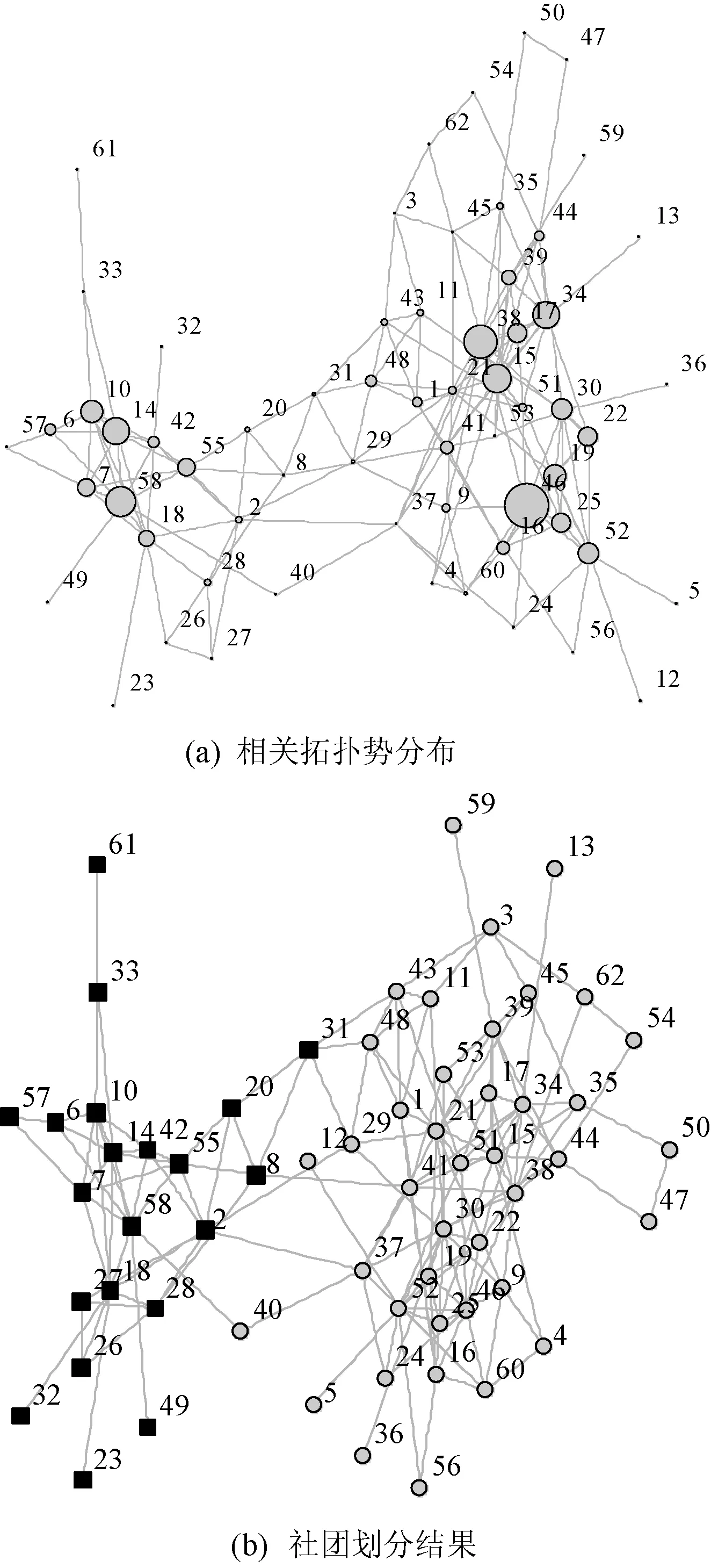
图5 宽吻海豚网络社团结构

将BITP算法和其他几种算法在这两个真实网络数据集上进行社团结构挖掘的结果进行对比分析。表2反映了这几种算法对应的模块度指标、NMI指标和VI指标。可以看出，本文算法在两个真实网络数据集上的NMI指标最高，VI指标最低。

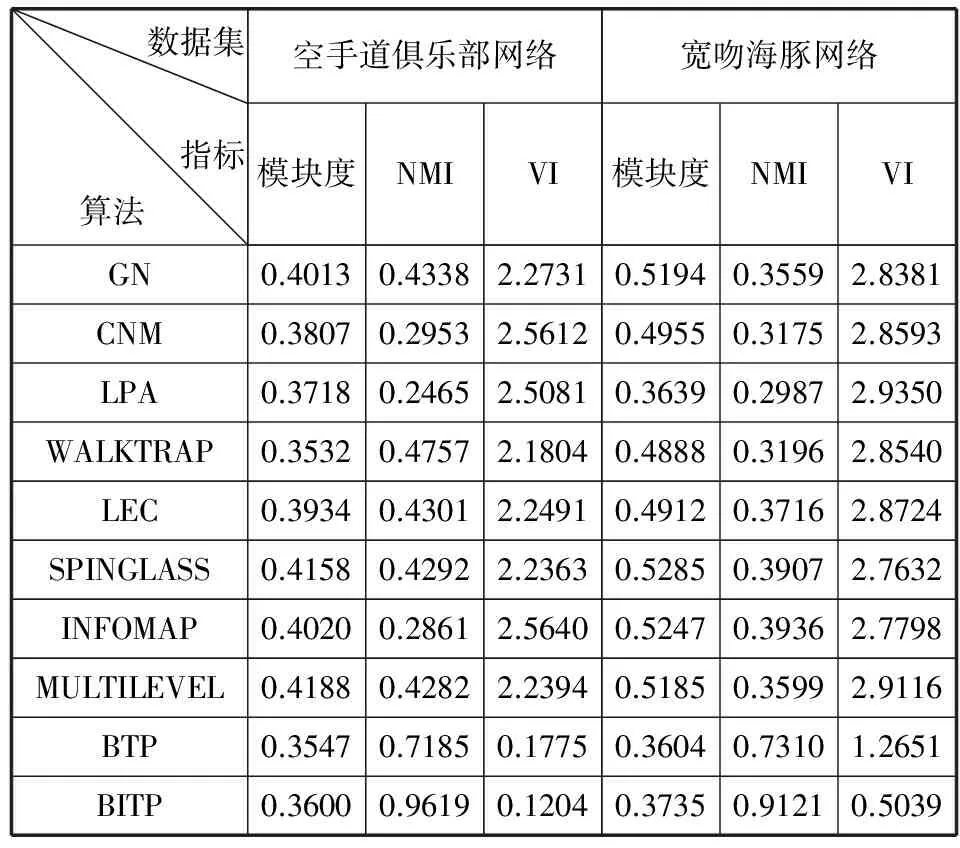
表2 几种算法对应的各种指标对比

5 结 语

本文提出了一种基于相关拓扑势的社团发现算法。算法将节点的相关性引入到拓扑势的计算中，并采用标签传播的方法控制社团规模。与几种传统的社团发现算法在人工合成网络和真实网络上进行验证，结果表明本文算法相对稳定且能够取得较高的社团划分精度。整个算法时间复杂度为O(n)，适合于大规模复杂网络的社团结构挖掘。针对现有社团结构研究大部分针对无向无权网络，下阶段考虑将基于拓扑势的算法应用到加权网络中，并进一步提高算法各方面的性能。

[1]GirvanM,NewmanMEJ.Communitystructureinsocialandbiologicalnetworks[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2002,99(12):7821-7826.

[2]NewmanMEJ.Detectingcommunitystructureinnetworks[J].TheEuropeanPhysicalJournalB-CondensedMatterandComplexSystems,2004,38(2):321-330.

[3]NewmanMEJ,GirvanM.Findingandevaluatingcommunitystructureinnetworks[J].PhysicalReviewE,2004,69(2):026113.

[4]ClausetA,NewmanMEJ,MooreC.Findingcommunitystructureinverylargenetwork[J].PhysicalReviewE,2004,70(6):066111.

[5]BlondelVD,GuillaumeJL,LambiotteR,etal.Fastunfoldingofcommunitiesinlargenetworks[J].JournalofStatisticalMechanics:TheoryandExperiment,2008(10):P10008.

[6]RaghavanUN,AlbertR,KumaraS.Nearlineartimealgorithmtodetectcommunitystructuresinlarge-scalenetworks[J].PhysicalReviewE,2007,76(3):036106.

[7]PonsP,LatapyM.Computingcommunitiesinlargenetworksusingrandomwalks[C]//Proceedingsofthe20thInternationalSymposiumonComputerandInformationSciences,2005:284-293.

[8]NewmanMEJ.Findingcommunitystructureusingtheeigenvectorsofmatrices[J].PhysicalReviewE,2006,74(3):036104.

[9]GfellerD,DeLRP.Spectralcoarsegrainingandsynchronizationinoscillatornetworks[J].PhysicalReviewLetters,2008,100(17):174104.

[10]RosvallM,BergstromCT.Mapsofrandomwalksoncomplexnetworksrevealcommunitystructure[J].ProceedingsoftheNationalAcademyofSciencesoftheUnitedStatesofAmerica,2008,105(4):1118-1123.

[11] 淦文燕,赫南,李德毅,等.一种基于拓扑势的网络社区发现算法[J].软件学报,2009,20(8):2241-2254.

[12] 张健沛,李泓波,杨静,等.基于拓扑势的网络社区节点重要度排序算法[J].哈尔滨工程大学学报,2012,33(6):745-752.

[13] 石立新,张俊星.基于势函数的标签传播社区发现算法[J].计算机应用,2010,34(3):738-741.

[14] 张桂杰,张健沛,杨静,等.基于拓扑势的局部化重叠社区识别[J].吉林大学学报:理学版,2015,53(4):730-738.

[15]ZhangY,WangJ,WangY,etal.Parallelcommunitydetectiononlargenetworkswithpropinquitydynamics[C]//Proceedingsofthe15thACMSIGKDDConferenceonKnowledgeDiscoveryandDataMining,2009:997-1006.

[16]GanWY.Studyontheclusteringproblemindatamining[D].Nanjing:NanjingUniversityofScienceandTechnology,2003.

[17]DanonL,Díaz-GuileraA,DuchJ,etal.Comparingcommunitystructureidentification[J].JournalofStatisticalMechanics:TheoryandExperiment,2005(9):P09008.

[18]MeilăM.Comparingclusteringsbythevariationofinformation[C]//16thAnnualConferenceonLearningTheoryand7thKernelWorkshop,2003:173-187.

[19]LancichinettiA,FortunatoS,RadicchiF.Bechmarkgraphsfortestingcommunitydetectionalgorithms[J].PhysicalReviewE,2008,78(4):046110.

[20]ZacharyWW.Aninformationflowmodelforconflictandfissioninsmallgroups[J].JournalofAnthropologicalResearch,1977,33(4):452-473.

[21]LusseauD,SchneiderK,BoisseauOJ,etal.ThebottlenosedolphincommunityofDoubtfulSoundfeaturesalargeproportionoflong-lastingassociations[J].BehavioralEcologyandSociobiology,2003,54(4):396-405.

COMMUNITY DETECTION ALGORITHM BASED ON INTERRELATED TOPOLOGICAL POTENTIAL

Zhao Wentao1,2Zhao Haohao1Meng Lingjun1

1(SchoolofComputerScienceandTechnology,HenanPolytechnicUniversity,Jiaozuo454000,Henan,China)2(KeyLaboratoryofMineInformationResearchatGeneralUniversitiesinHenanProvince,Jiaozuo454000,Henan,China)

Since the traditional methods obtain low precision in division and low resolution in module function, an algorithm of community detection BITP is proposed based on the interrelated topological potential. The algorithm introduces the interrelated topological potential to evaluate the influence of nodes by considering the correlation factor between nodes. The nodes with extreme potential are searched at first. The sizes of the local communities are controlled by adopting the method of label propagation. The experimental results on synthetic and real-world networks show that the proposed algorithm is relatively stable and achieves higher precision. It is more suitable for detecting community structure in large-scaled and complex networks with a time complexity ofO(n)andnopriorknowledge.

Community structure Complex network Interrelated topological potential Label propagation

2015-09-17。河南省科技攻关计划项目(142102210435)；河南省高等学校矿山信息化重点学科开放实验室开放基金项目(ky2012-02)。赵文涛，教授，主研领域：数据库，数据挖掘，大数据。赵好好，硕士生。孟令军，硕士生。

TP

ADOI:10.3969/j.issn.1000-386x.2017.01.047