重型车辆重心高度在线自适应估计方法研究

付志军，谢伟东

(浙江工业大学 机械工程学院，浙江 杭州 310014)

重型车辆重心高度在线自适应估计方法研究

付志军，谢伟东

(浙江工业大学 机械工程学院，浙江 杭州 310014)

为准确获取影响重型车辆侧向稳定性控制的关键参数重心高度，提出了一种由参数误差信息驱动的新的重型车辆重心高度在线自适应估计方法.该方法与一般的递推最小二乘(RLS)估计方法不同的是，在设计在线自适应学习律时考虑了参数误差信号，从而提高了算法的鲁棒性和收敛速度，并且该方法只需要知道侧倾角和侧向加速度信号，避免了一般观测方法所需的侧倾角速度和侧倾角加速度等高阶信号所带来的噪声干扰问题.李雅普诺夫方程证明了所提重心高度在线观测方法的稳定性，仿真结果也验证了所提估计方法的有效性.

重型车辆；参数估计；重心高度；侧向稳定性

安全、节能和环保成为汽车发展的三大主题，而安全性则是从事汽车设计的研究人员与车辆使用者最关心的问题之一.在所有交通事故中，车辆侧翻是一种极其危险的恶性交通事故，常常会带来严重的后果.由于较高的重心高度和较低的轮宽与重心高度之比值使得重型车辆比一般车辆更容易丧失侧向稳定性.美国高速公路交通安全管理局(NHTSA)研究表明，侧翻事故在非碰撞导致的第一类有害致命交通事故中大约占90%的比例，相比其他事故，重型车辆侧翻事故往往造成更严重的伤害，对经济社会和个人造成很大影响.《国家中长期科学和技术发展规划纲要(2006—2020年)》中明确将重点开发交通故预防预警、主动安全控制及应急处理技术列为交通运输业领域作为优先主题.重心高度的在线估计对开发有效的侧翻预警和防侧翻控制系统意义重大.通过对重心高度的在线估计，可获得车辆侧翻静态稳定阈值(SSF)[1]和侧拉率(SPR)[2]及车辆的动态侧翻预警指标[3].

有关车辆重心高度在线估计可分成3类：1) 基于传递函数的估计方法[4-5]；2) 基于卡尔曼滤波观测器的估计方法[6-7]；3) 递推最小二乘算法(RLS)估计方法[8-10].基于传递函数的估计方法的缺点是需要通过大量的离线训练数据来获得相关参数，不能在线更新.卡尔曼滤波是以最小均方误差为估计的最佳准则，来寻求一套递推估计的算法，其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，当运动目标长时间被遮挡时会存在目标跟踪丢失的情况.递推最小二乘(RLS)估计方法被证明是一种比较有效的在线估计方法[11-13].其缺点在于:当信噪比较小时可能存在多个局部极小点，使得估计结果不能保证收敛到全局最小点，即参数真值.面对实际工程问题，除了系统的收敛性外，往往更关心其有限时间收敛问题[14].控制领域的最近研究表明[15-16]：把参数误差信息考虑到在线自适应学习率中可以提高收敛速度和增强鲁棒性.受此启发，提出一种参数误差信息驱动的重型车辆重心高度在线自适应估计方法.该方法可以保证在状态估计误差收敛的同时参数估计误差也收敛到实际值.该方法通过设计递归滤波矩阵仅需要侧倾角和侧向加速度信号就可以实现重心高度的估计，避免了侧倾角速度和侧倾角加速度等高阶信号所带来的噪声干扰问题，便于实际应用.

1 估计模型

侧翻指标是用来衡量车辆侧翻的可能性，并且及时的触发防侧翻控制系统预防车辆侧翻的发生，其定义为

(1)

其中：FL，FR分别为左、右车轮受地面垂向载荷；R为侧翻指数.当R=±1时，代表一侧车轮离地，这时车辆将发生侧翻；汽车在平直路面上直线行驶时R=0.

假设簧载质量的侧倾主要是由车辆的侧向加速度引起的，忽略路面垂直激励和非簧载质量的影响，则侧翻指标可以进一步被表示为

(2)

其中：a为侧向加速度；φ为侧倾角；h为重心高度；T为轮距.

由式(2)可以看出：侧翻指标需要知道侧向加速度、侧倾角外和重心高度，而重心高度一般不能直接获得，需要通过相关方法进行在线估计(图1).图1为常用的重心高度估计模型.

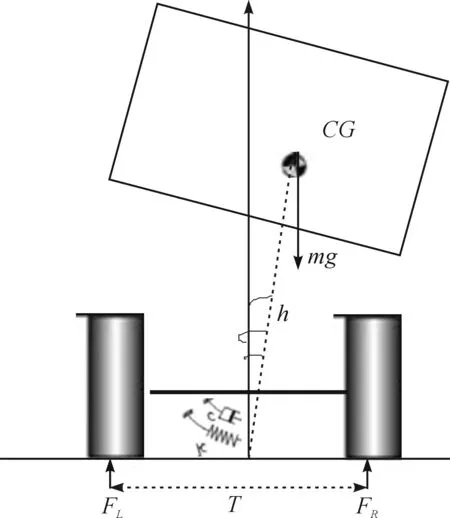
图1 车辆侧倾模型Fig.1 Vehicle roll plane model

根据动力学基本原理可以得到如下的车辆侧倾动力学方程为

(3)

式中：Jxeq=Jxx+mh2为等效侧倾转动惯量；Jxx为侧倾转动惯量；c为侧倾阻尼；k为侧倾刚度.

进一步可以把式(3)写成一般的参数辨识的形式，即

y=ψTθ+ξ

(4)

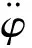
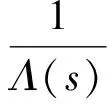
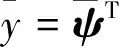
(5)

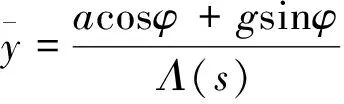
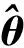
(6)

2 估计方法

受文献[15]正弦信号的估计方法的启发，提出了一种由参数误差信息驱动的估计方法.首先设计相关滤波辅助变量，即

(7)

式中：l>0,η>0分别为设计的滤波常数.

进一步设计滤波回归矩阵E(t)和F(t)方程分别为

(8)

于是可以得到在线适应学习率，即

(9)

式(9)可以保证在状态估计误差指数收敛的同时参数估计误差也指数收敛到零，在有外界干扰的情况下一致最终有界(UUB).

证明 构建李雅普诺夫函数为

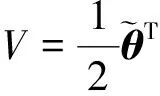
(10)

由式(7，8)可得

(11)

在外界干扰等于零的情况下，由(10，11)可得

(12)

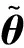
在外界干扰不等于零的情况下，得

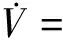
(13)

3 仿真验证

在MATLAB/Simulink中编写估计算法，与多体动力学仿真软件进行联合仿真，验证所提重心高度估计方法的准确性.所用车辆选择为中型的长途客车，车辆类别为Tour Bus 5.5T/10T，簧载质量为6 360 kg，簧载质量转动惯量Jxx=7 695.6 kg·m2，参考质心高度为1.2 m，轮距为1.75 m，悬架侧倾刚度为303 767 N·m/rad，悬架侧倾阻尼为15 910 N·m·s/rad.

所提估计方法(图2)将和带遗忘因子的递归最小二乘法(RLS)做比较，即

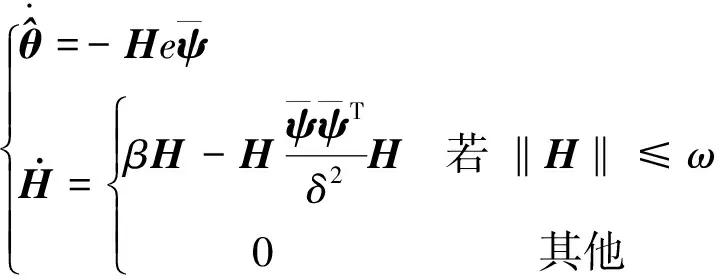
(14)

其中：β为遗忘因子；ω为设计常数.

图2 估计方法系统框图Fig.2 The block diagram of estimation method

客车的行驶速度为60km/h，方向盘转角输入如图3所示，仿真结果如图4～6所示.

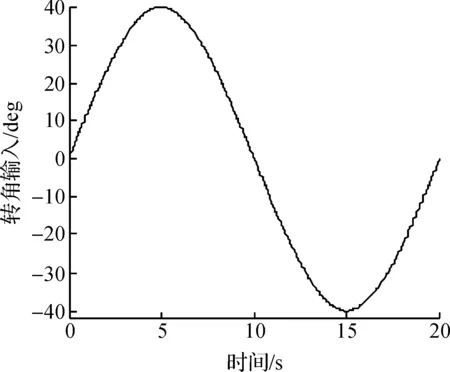
图3 方向盘转角Fig.3 Steering angle input

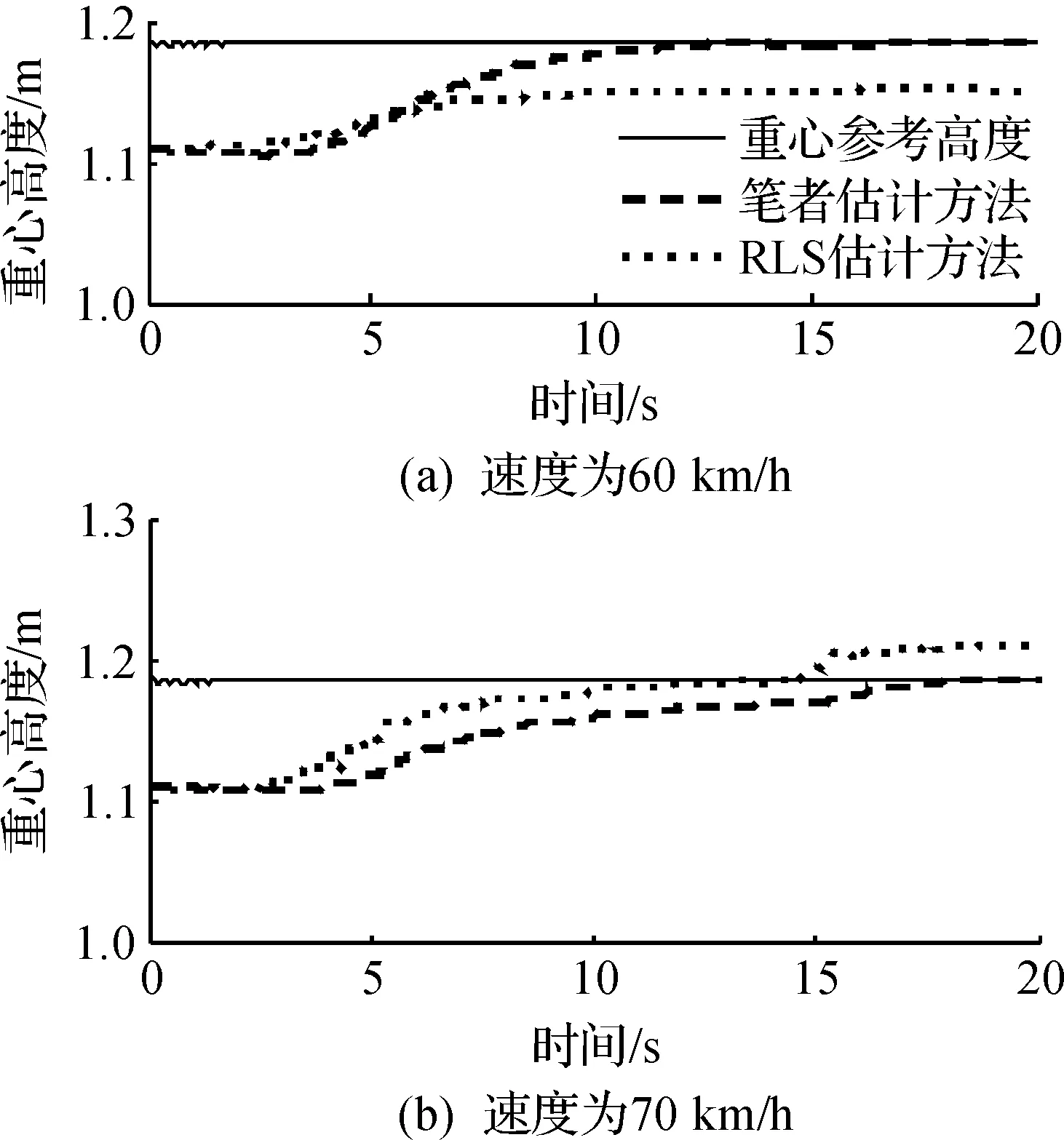
图4 重心高度估计结果Fig.4 Estimation result of CG height

图5 侧倾刚度Fig.5 Roll stiffness

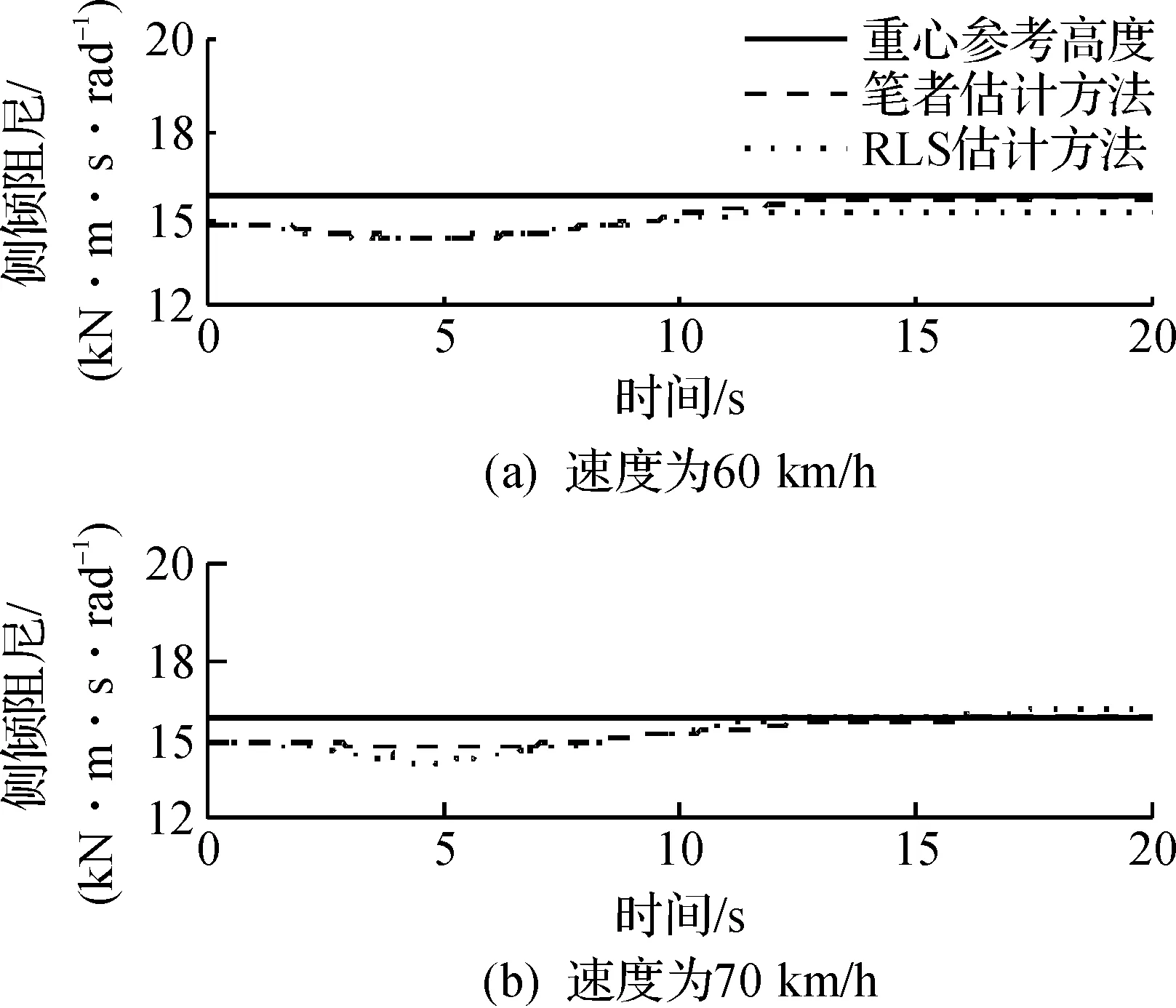
图6 侧倾阻尼Fig.6 Roll damping

由图4可知：图4(a)估计方法具有可以很快的跟踪到实际参考值，而对于RLS估计方法则存在一定的稳态误差；当速度变化时，图4(b)估计方法依然可以很快的跟踪的实际参考值，而RLS估计方法则存在较小的波动，且依然存在稳态误差.其主要原因是RLS估计方法的收敛性主要由观测误差来决定，因此，不能保证收敛到全局最小点，即参数真值.而笔者所提的估计方法，由于在设计自适应率时，考虑了参数误差因素，使得其具有更快的收敛速度和较好的鲁棒性能.相似的估计结果可以从图5的侧倾刚度的估计结果和图6的侧倾阻尼的估计结果中得到进一步验证.综上，图4～6的估计结果验证了所提估计方法的有效性.

4 结 论

设计了一种基于参数误差信息驱动的重型车辆重心高度在线估计方法.该估计方法由参数误差信息来驱动自适应率，而不像一般的RLS估计方法由观测误差所驱动，从而大大提高了收敛速度和稳态性能.该方法能实现在线估计重心高度的情况下，同时估计侧倾刚度和阻尼；准确在线估计重心高度为将来开发侧翻预警系统奠定了基础.仿真结果验证了所提估计方法的有效性.下一步的研究工作可在此研究基础上开发有效的防侧翻预警和控制系统.

[1]WALZMC.Trendsinthestaticstabilityfactorofpassengercars,lighttrucks,andvans[R].Virginia:Springfield,2005.

[2]CHOUT,CHUTW.Animprovementinrolloverdetectionofarticulatedvehiclesusingthegreysystemtheory[J].Vehiclesystemdynamics,2014,52(5):67-177.

[3]CHADL,DAMRONGRITP,VASILIOST,etal.Anewpredictivelateralloadtransferratioforrolloverpreventionsystems[J].IEEEtransactiononvehicletechnology,2013,62(7):2928-2936.

[4]FUJIOM.Gravitycenterheightestimationfortherollovercompensationsystemofcommercialvehicles[J].JSAEreview,1999,20:493-497.

[5] WESEMEIER D, ISERMANN R. Identification of vehicle parameters using stationary driving[J]. Control engineering practice,2009,17(12):1426-1431.

[6] HUANG X, WANG J. Center of gravity height real-time estimation for lightweight vehicles using tire instant effective radius[J]. Control engineering practice,2013,21:370-380.

[7] CHENG C, CEBON D. Parameter and state estimation for articulated heavy vehicles[J]. Vehicle system dynamic,2011,49(1):399-4182.

[8] HUANG X, WANG J. Longitudinal motion based lightweight vehicle payload parameter real-time estimations[J]. ASME journal of dynamic system and measurement control.2013,135(1):1-10.

[9] RAJAMANI R, PIYABONGKARN D, TSOURAPAS V et al. Parameter and state estimation in vehicle roll dynamics[J]. IEEE transaction on intelligent transportation system,2011,12(4):1558-1567.

[10] RAJAMANI R，PIYABONGKARN D，TSOURAPAS V，et al. Real-time estimation of roll angle and CG height for active rollover prevention applications[C]// American Control Conference. Saint-Louis: IEEE,2009.

[11] 杨秀建，李海青，高晋，等.基于递推最小二乘法的半挂汽车列车结构参数估计[J].昆明理工大学学报(自然科学版)，2014，39(3)：43-49.

[12] 王卫红，琚波，杨洁，等.一种基于最小二乘估计的LTEMR电平信号定位方法[J].浙江工业大学学报，2015，43(5)：487-491.

[13] 王理同.生长曲线模型中最小二乘估计与极大似然估计的近似等价性.[J].浙江工业大学学报，2012，2(2)：233-236.

[14] 孙明轩，余轩峰，孔颖.终态神经计算：有限时间收敛性与相关应用[J].浙江工业大学学报，2015，4(3)：311-317.

[15] NA J，YANG J，WU X，et al. Robust adaptive parameter estimation of sinusoidal signals[J]. Automatic，2015，53：376-384.

[16] LI G，NA J，REN X. Adaptive neural network feedforward control for dynamically substructured systems[J]. IEEE transaction on control system technology，2014，22(3)：944-954.

[17] 陈慧，高博麟，徐帆.车辆质心侧偏角估计综述[J].机械工程学报，2013，49(24)：76-94.

Adaptive online estimation of center of gravity height of heavy vehicle

FU Zhijun, XIE Weidong

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

In order to get the center of gravity (CG) height of heavy vehicle which is key parameter affecting the vehicle lateral stability, a novel parameter error driven robust estimation method is proposed for online estimation of CG height of heavy vehicle. Unlike the commonly used RLS method, a parameter error driven updating law is synthesized to ensure rapid and robust convergence. Moreover, the proposed method is directly based on measurable roll angle of the sprung mass, while the high order signals like roll rate and roll acceleration are not needed, so the noise disturbance is avoided. The stability of the proposed estimation method is illustrated using the Lyapunov approach. The validity of the proposed estimation method is verified with the simulation results.

heavy vehicle; parameter estimation; CG height; lateral stability

(责任编辑：刘 岩)

2016-04-27

国家自然科学基金资助项目(51405436)；浙江省公益性基金资助项目(2014C31101)

付志军(1982—)，男，河南林州人，讲师，博士后，研究方向为车辆动力学建模与控制，E-mail：fuzhijun@zjut.edu.cn.

U461.6

A

1006-4303(2017)01-0104-04