变结构遗传最小二乘支持向量机法预测日用水量

陈 磊，石 也

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

变结构遗传最小二乘支持向量机法预测日用水量

陈 磊，石 也

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

为解决日用水量预测模型的动态参数估计问题，提出了基于变结构遗传最小二乘支持向量机的预测模型.以日用水量的主要影响因素和相关日用水量为输入，利用遗传算法对基于LSSVM的历史日用水量模型参数进行寻优，获得模型结构参数序列；采用扩展卡尔曼滤波器估计基于最小二乘支持向量机的预测日用水量模型参数，进而预测下一日用水量.实例分析表明：提出的模型具有较高的预测精度，预测的最大绝对相对误差仅为9.3%，平均绝对相对误差为2.09%.

遗传算法；最小二乘支持向量机；变结构；扩展卡尔曼滤波；日用水量

科学的管网调度能节省大量的供水能耗，全面提高管网的安全性和可靠性，但调度方案是否可行很大程度上取决于日用水量的预测精度.针对日用水量的非线性特征，学者们一般以预测日用水量的相关日用水量和主要影响因素为输入，采用具有较强非线性映射能力的神经网络[1-2]和支持向量机[3-4]进行预测，但他们都未提及预测前是否需要以及如何持续动态更新模型参数的方法.BAI Yun等[5]提出根据历史日用水量模型的参数，采用卡尔曼滤波法估计预测日用水量的模型参数，实现了日用水量模型参数的动态更新.然而其采用交叉验证法确定历史日用水量模型参数耗时较长，获得的优化模型参数也很大程度上取决于模型参数区间以及参数网格的划分，难以保证获得较优的模型参数，并且其模型输入仅考虑日用水量历史序列，当日用水量变化较大时，采用更新参数的模型仍会出现较大的预测误差.为此，模型的输入增加了日用水量的主要影响因素，并利用具有较强全局寻优能力的自适应遗传算法对历史日用水量模型的参数组寻优，得到较优的参数组序列.根据参数组序列采用卡尔曼滤波法估计预测日模型的参数，实现预测日用水量的更高精度预测.

1 遗传最小二乘支持向量机(GA-LSSVM)模型

1.1 最小二乘支持向量机

最小二乘支持向量机[6](LSSVM)是对支持向量机[7](SVM)改进的算法，它采用等式约束替代SVM的不等式约束，将SVM的二次规划转变为线性问题，寻优空间从SVM的三维降低到LSSVM的二维.与SVM相比，LSSVM具有更少的参数和更快的训练速度.

(1)

式中：ω为权矢量，ω∈Rnf；ei为误差，ei∈R；γ为惩罚因子；φ(·)为核函数，φ(·):Rn→Rnf；b为偏置.

为求解最小值，可构造函数式

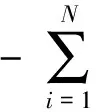
(2)

式中αi为拉格朗日系数.

根据KKT条件，对式(2)求偏导，即

(3)

消去ω和e后变为线性方程

(4)

式中：y=[y1,y2,…,yn]T,1v=[1,1,…,1]T，α=[α1,α2,…,αn]T；I为N×N的单位矩阵；Ωij=φ(xi)Tφ(xj)=K(xi,xj),i,j=1,2,…,N.

根据式(4)得到α和b，则LSSVM的估计函数为

(5)

式中径向基核函数K(x,xi)=exp{-‖x-xi‖2/σ2}.

LSSVM一般采用网格交叉验证法来确定宽度系数σ和惩罚因子γ两个参数，但该方法耗时长，并且如何选择参数范围和划分网格对结果影响较大.

1.2 遗传算法优化LSSVM参数

传统遗传算法(GA)简单实用，但是收敛速度较慢，采用随个体适应值自适应调整交叉和变异概率，具有较强全局搜索能力的自适应遗传算法[8]来优化LSSVM的参数σ,γ.

优化步骤如下：

1)σ,γ的取值范围：σ∈[0.01,50]，γ∈[0.01,50].两参数采用12位二进制编码，遗传算法的每个个体为24位.

2)根据个体的适应值，利用轮盘赌法从父代选出相同数目的较优个体.

3)自适应交叉和变异.

采用两位交叉，自适应交叉概率计算表达式为

(6)

式中：f′为两个体中较大的适应值；favg为种群平均适应值；fmax为种群最大适应值.

变异方式为：对所有个体的每位二进制编码从0～1的范围内随机产生一个数，若其大于个体的变异率，则编码将从0变1或从1变0，否则不变.

自适应变异概率计算方法为

(7)

式中f为变异个体的适应值.

4)保留较优个体.父代中一半适应值较小的个体由子代中适应值较大的个体替代.

2 扩展卡尔曼滤波器(Extended kalman filter, EKF)

由于所建模型涉及非线性系统状态及参数估计问题，因此采用扩展卡尔曼滤波器[9].该算法利用一个系统状态方程和一个测量更新方程来描述线性动态过程，形成一种递推滤波.

系统的状态方程和测量方程分别为

x(k)=f(x(k-1),u(k-1))+w(k-1)

(8)

y(k)=g(x(k))+v(k)

(9)

式中:u为控制矢量；x为状态矢量；y为观测矢量；w和v分别为过程噪声和观测噪声，假设它们独立，并分别服从正态分布的高斯白色噪声w～N(0,Q),v～N(0,R)，则

E[w(k-1)]=0，E[v(k-1)]=0

(10)

过程噪声Q和观测噪声R的方差分别为

E[w(k-1)wT(l-1)]=Q(k-1)

E[v(k-1)vT(l-1)]=R(k-1),k≠l

(11)

利用EKF计算模型参数，计算过程可分两个阶段：

1)预测阶段

2)更新阶段

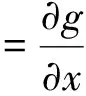
3 变结构遗传最小二乘支持向量机模型(VSG-LSSVM模型)

由于隔年变化的日用水量具有很强的相似性，因此模型采用365 d的等维样本长度.采用等维的数据，以预测日用水量的主要影响因素(包括平均温度、最低温度、最高温度、阴晴量、相对湿度及星期量)和高度相关日用水量为输入，以预测日用水量为输出，建立遗传最小二乘支持向量机模型(GA-LSSVM模型).通过计算日用水量序列的自相关系数[10]，发现预测日与预测日前第7 d的日用水量高度相关，因此取预测日前第7 d的日用水量为输入.

由于相同季节内有相似的气候和用水量情况，日用水量模型参数也存在相似性，因此EKF模型参数组序列取92组(1年中最大的季节天数).为了确定预测日用水量的模型参数，需先分别采用GA确定对预测日前92 d的日用水量进行预测的92个模型参数，根据92个模型参数组利用扩展卡尔曼滤波估计预测日模型参数，建立变结构遗传最小二乘支持向量机模型(VSG-LSSVM模型)，从而对预测日用水量进行预测.

建模和预测具体过程如下：

图1 VSG-LSSVM建模Fig.1 Daily water consumption forecasting modeling based on VSG-LSSVM

2) 若t=1，模型参数组序列保持不变；否则，将最新获得(t+455) d的日用水量数据加入到用于确定最新模型参数(σt+91,γt+91)的等维365组的训练样本，抛弃该样本中第(t+90) d的日用水量数据，以(t+91)～(t+455) d共365组数据构建新的训练样本，将该样本5等分，利用自适应遗传算法对LSSVM的模型参数进行寻优(采用5折交叉验证来评价遗传算法个体适应函数值)，得到(σt+91,γt+91)，去掉原模型参数序列中的(σt-1,γt-1)，组成新的92组较优参数(σt,γt)，(σt+1,γt+1)，…，(σt+91,γt+91).

5) 判断t是否等于预测天数274：若是，转步骤6)，若否，t=t+1，返回步骤2).

6) 程序结束.

实际日用水量与GA-LSSVM模型、VSG-LSSVM模型预测结果的对比见图2.GA-LSSVM模型预测的最大绝对相对误差为13.7%(第645 d)，VSG-LSSVM模型预测的最大绝对相对误差为9.3%(第484 d).

图2 实际日用水量和2种模型预测值对比Fig.2 Comparison of daily water consumption between real and two prediction models

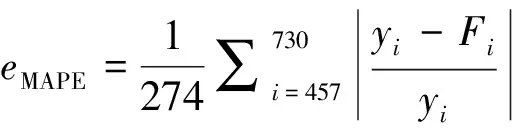
表1 两模型预测误差分布对比

Table 1 The comparison of predicted relative error between two models

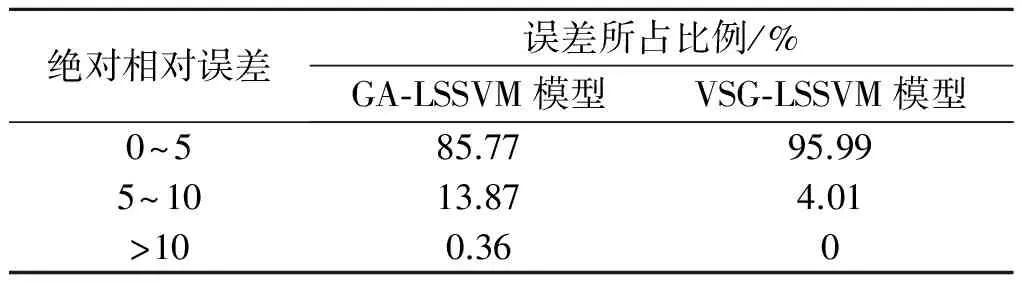
绝对相对误差误差所占比例/%GA⁃LSSVM模型VSG⁃LSSVM模型0～585．7795．995～1013．874．01>100．360

由图2以及两模型预测误差的分布可知：VSG-LSSVM模型总体的预测精度明显高于GA-LSSVM模型.在预测前期(457～486 d)，扩展卡尔曼滤波参数需要根据模型参数组序列进行调整，因此30 d中仅有7 d的VSG-LSSVM模型预测结果优于GA-LSSVM模型.但在第487 d后，244 d中有165 d的VSG-LSSVM模型预测结果优于GA-LSSVM模型，VSG-LSSVM模型的预测精度有显著提高.

4 结 论

对传统日用水量模型参数的预测方法进行了改进，提出了日用水量模型参数的动态预测方法.利用具有较强全局搜索能力的自适应遗传算法对历史日用水量的模型参数进行寻优，得到较优的模型参数序列；根据序列采用具有较强非线性估计能力的卡尔曼滤波法推断基于最小二乘支持向量机的预测模型参数，实现参数的精确估计.实例分析结果表明：该模型预测的最大绝对相对误差、平均绝对相对误差以及预测误差分布都较大程度优于传统基于遗传最小支持向量机的预测模型，可用于长期日用水量预测.

[1] BABEL M S, SHINDE V R. Identifying prominent explanatory variables for water demand prediction using artificial neural networks: a case study of Bangkok [J]. Water resources management,2011,25(6):1653-1676.

[2] 袁一星，兰宏娟，赵洪宾，等.城市用水量BP网络预测模型[J].哈尔滨建筑大学学报,2002,35(3):56-58.

[3] 王亮，张宏伟，牛志广.支持向量机在城市用水量短期预测中的应用[J].天津大学学报，2005，38(11)：1021-1025.

[4] 陈磊，余翔.遗传最小二乘支持向量机法预测日用水量[J].节水灌溉，2012(8):4-7.

[5] BAI Yun, WANG Pu, LI Chuan, et al. Dynamic forecast of daily urban water consumption using a variable-structure support vector regression model[J]. Journal of water resource planning and management，2015，141(3):1-10.

[6] SUYKEN J A K, VAN G T, DE M B, et al. Least squares support vector machines[M]. Singapore: World Scientific，2002.

[7] 陈磊，董志勇.支持向量机在短期用水量预测中的应用[J].浙江工业大学学报，2007，35(4)：448-451.

[8] 王小平，曹力明.遗传算法-理论、应用与软件实现[M].西安：西安交通大学出版社，2002.

[9] ANDERSON B, MOORE J. Optimal filtering [M]. New Jersey: Prentice-Hall，1979.

[10] 丁晶,邓育仁.随机水文学[M].成都：成都科技大学出版社，1988.

Daily water demand forecasting method based on variable structure genetic least squares support vector machine

CHEN Lei, SHI Ye

(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

To dynamically estimate the parameters of daily water consumption model，a new variable-structure genetic least squares vector machine(LSSVM)-based model is proposed. The principal factors of daily water consumption and the correlative daily water consumption are used as the model inputs. With genetic algorithm, the parametersseries of LSSVM-based historical daily water consumption models aredetermined. With the series, Extended Kalman Filter(EKF) is applied to estimate the parameters of LSSVM-based next-day prediction modeland the next-day daily water consumption is forecasted. Case study shows that the proposed model has higher forecasting performance in term of a maximum absolute relative error of 9.3% and a mean absolute relative error of 2.09%.

genetic algorithm; least squares vector machine; variable structure; extended Kalman Filter; daily water consumption

(责任编辑：刘 岩)

2016-04-07

国家自然科学基金资助项目(50908165)；浙江省饮用水安全保障与城市水环境治理重点科技创新团队项目(2010R50037)

陈 磊(1977—)，男，浙江衢州人，副教授，博士，主要从事给水管网系统建模和优化研究，E-mail：zj_chen_lei@sina.com.cn.

TU991.33

A

1006-4303(2017)01-0069-04