一类分数阶反应扩散方程的差分方法

刘桃花，侯木舟

(1.中南大学数学与统计学院，中国 长沙 410083; 2.邵阳学院理学系，中国 邵阳 422004)

一类分数阶反应扩散方程的差分方法

刘桃花1,2，侯木舟1

(1.中南大学数学与统计学院，中国 长沙 410083; 2.邵阳学院理学系，中国 邵阳 422004)

分数阶反应扩散方程可以用来模拟反常扩散运动，它是由传统的反应扩散方程演变而来的.本文对带变系数的空间分数阶反应扩散方程的初边值问题进行了数值研究，采用了移位的Grunwald公式对空间分数阶导数进行离散，在此基础上建立了经典的隐性Euler差分格式.然后讨论了该格式的解的存在唯一性，分析了该方法相容性、稳定性及收敛性，得到了O(τ+h)收敛阶.最后用数值实验证明了该格式的有效性.

分数阶反应扩散方程； 隐性Euler差分格式；相容性；无条件稳定；收敛性

分数阶(空间分数阶、时间分数阶和空间-时间分数阶)反应扩散方程是传统的整数阶反应扩散方程的推广,即用分数阶导数代替相应的整数阶导数[1].由于分数阶微分方程比整数阶方程更精确地描述了客观世界,因此它在描述自然界扩散现象中起到非常重要的作用,已广泛地应用于物理[2-4]、化学[5]、环境[6]等领域.空间分数阶反应扩散方程被用来模拟反常扩散运动，若粒子以连续方式扩散，就是经典的布朗模型.

本文将考虑如下带变系数的空间分数阶反应扩散方程：

(1)

初边值条件为：

c(x,0)=s(x),L≤x≤R,

(2)

c(L,t)=0,c(R,t)=b(t),t≥0.

(3)

其中扩散系数d(x)≥0;v(x)≥0,耗散系数 p(x)≥0，均为[L,R]上的连续函数.

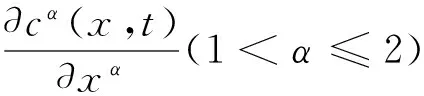
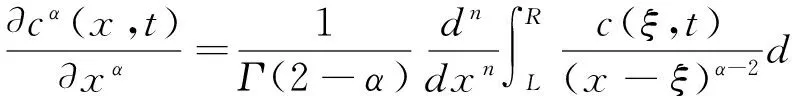
(4)

目前,已有很多学者研究其解的存在性和唯一性，取得了很好的结果[9-10].关于同类别的问题的数值方法有很多学者进行了研究[11-14]，Xie等[15]在研究空气中PM2.5的扩散情况时，给出了此类分数阶扩散方程的Crank-Nicholson格式.本文在采用移位Grunwald公式对空间分数阶导数进行离散，构造了经典的隐性Eluer差分格式来求出此方程的数值解.

文章其它部分安排如下：第2部分，对带变系数的空间分数阶的分数阶扩散方程构建了隐性Eluer差分方法并证明其解的存在唯一性，以及稳定性、收敛性.第3部分，给出一个数值实验，来检验此方法的有效性.

1 差分格式的建立

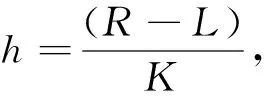
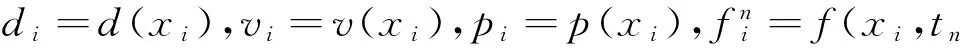
(5)

其中gk为Grunwald权系数

定义一阶空间及时间导数：

其中，τ=Δt，因此，可得到

(6)

存在M为正常数，使得：

|Ri,n+1|≤M(τ+h).

由上式，对问题(1)～(3)可以建立隐性的Eluer格式如下：

(7)

(8)

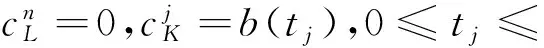
(9)

由上可知式(7)～(9)与带初边值条件方程(1)～(3)相容.

方程(7)通过整理得如下形式

(10)

(Ei=viΔt/h,Bi=diΔt/hα).

可进一步将分数阶方程改写为矩阵形式

ACn+1=Cn+ΔtFn+1,

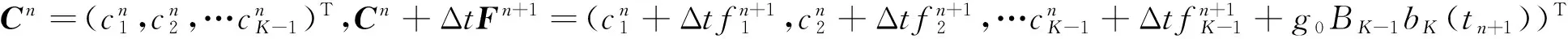
A=[Ai,j]是一个(K-1)×(K-1)系数矩阵，当i=1,…,K-1和j=1,…,K-1时

(11)

2 差分格式的差分解的存在唯一性以及稳定性及收敛性分析

引理1[10]当1<α≤2时，Grunwald权系数gi(i=0,1,2,…)满足：

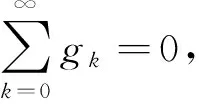
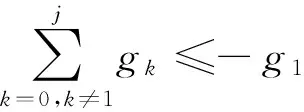
定理2 差分格式(6)～(8)的解存在唯一，而且差分格式是无条件稳定的.

证 假设λ为矩阵A的特征值，X为其对应的特征向量，即AX=λX，设

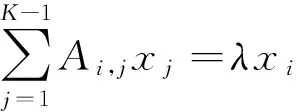
(12)

将式(11)代入式(12)得

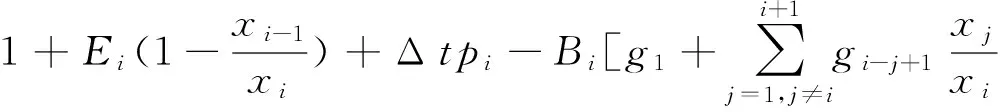
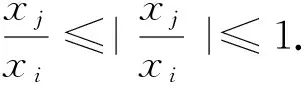
命题1 上面分析时，已知该方法是相容的，且得到该方法的截断误差为O(τ+h).根据Lax等价定理[16]，差分格式(6)～(8)的解cn以‖·‖∞收敛到初边 值问题的解，且收敛阶为O(τ+h).

3 数值实验

考虑如下分数阶反应扩散方程(α=1.5)

图1 数值结果Fig.1 Numerical results

此方程的精确解为c(x,t)=x2e-t

图1数值结果表明，在T=1时刻，取相同的空间、时间步长(τ=h=1/10)时，方程数值解与精确解相吻合，即所给出差分格式是有效的.

表1为T=1时刻，取相同的空间、时间步长时，数值解的最大误差及误差阶.在表1中，当空间步长和时间步长都减半时，误差接近原来的一半，这表明差分格式的收敛阶为O(τ+h).

表1 最大误差及误差阶

Tab.1 Max error and error rate

τ=h最大误差误差阶1/108.03228×10-31/204.21272×10-31.906671/402.17059×10-31.940821/801.22580×10-31.77075

[1] METZLER R,KLAFTER J.The random walk’s guide to anomalous diffusion:A fractional dynamics approach[J].Phys Rep,2000,339(1):1-77.

[2] SAICHEV A I,ZASLAVSKY G M.Fractional kinetic equations:solutions and applications[J].Chaos,1997,7(4):753-764.

[3] ROSSILIHIN Y,SHITIKOVA M.Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids[J].Appl Mech Rev,1997,50(2):15-67.

[4] METZLER R,KLAFTER J.Boundary value problems for fractional diffusion equations[J].Phys A:Stat Mech Appl,2000,278(1-2):107-125.

[5] YUSTE S B,LINDENBERG K.Subdiffusion-limited A+A reactions[J].Phys Rev Lett,2001,87(11):118-301.

[6] BENSON D A,WHEATCRAFT S W,MEERSCHAERT M M.Application of a fractional advection-dispersion equation[J].Water Resour Res,2000,36(6):1403-1412.

[7] TADJERAN C,MEERSCHAERT M M,SCHEFFLER H P.A second-order accurate numerical approximation for the fractional diffusion equation[J].J Comput Phys,2006,213(1):205-213.

[8] TUAN V K,GORENFLO R.Extrapolation to the limit for numerical fractional differentiation[J].Z Agnew Math Mech,1995,75:646-648.

[9] KEMPPAINEN J.Existence and uniqueness of the solution for a time-fractional diffusion equation with Robin boundary condition [J].Abstr Appl Anal Article,2011,(11):ID321903.

[10] PODLUBNY I.Fractional Differential Equations,Volume 198.An introduction to fractional derivatives,fractional differential equations,to methods of their solution and some of their applications[M].San Diego:Academic Press,1998.

[11] MEERSCHAERT M M.TADJERAN C.Finite difference approximations for fractional advection-dispersion flow equations[J].J Comput Appl Math,2004,172(1):65-77.

[12] LIU F,ANH V,TURNER I.Numerical solution of space fractional Fokker-Planck equation[J].Comp Appl Math,2004,(166):209-219.

[13] 尹修草，周 均，胡 兵.分数阶对流-弥散方程的有限差分方法[J].四川大学学报(自然科学版),2013,50(3):409-413.

[14] FIX G J,ROOP J P.Least squares finite-element solution of a fractional order two-point boundary value problem[J].Comput Math Appl,2004,48(7-8):1017-1033.

[15] XIE C P,LI L,HUANG Z Z,etal.Fractional difference approximations for fractional reaction-diffusion equations and the application in PM2.5[C].International Symposium on Energy Science and Chemical Engineering,2015-12,Guangzhou.

[16] CHAVES A.Fractional diffusion equation to describe Levy flights[J].Phys Lett A,1998,239(1-2):13-16.

(编辑 HWJ)

Finite Difference Approximations for Fractional Reaction-Diffusion Equations

LIUTao-hua1,2*,HOUMu-zhou1

(1.School of Mathematics and Statistics,Central South University,Changsha 410083,China；2.Department of Science,Shaoyang University,Shaoyang 422004,China)

Fractional reaction-diffusion equations are generalizations of classical reaction-diffusion equations,which are used in simulating the anomalous diffusion motion.In this paper,we examine a practical numerical method,which is called Euler method to solve a class of initial-boundary value a fractional reaction-diffusion equation with variable coefficients.Then we discuss the existence and uniqueness of solutions for the format.The stability,consistency and convergence of the method are established to get the convergence order ofO(τ+h).Finally,we use a numerical experiment to prove the effectiveness of the proposed format.

fractional reaction-diffusion equations; implicit Euler method; consistency; unconditional stability; convergence

10.7612/j.issn.1000-2537.2017.01.014

2016-09-04

国家自然科学基金资助项目(61672356,61375063,61271355,11271378,11301549)；中南大学2015年实验室研究项目

* 通讯作者,E-mail：liutaohua2005@163.com

O241.82

A

1000-2537(2017)01-0091-04