双馈风电场AVC系统协调优化控制策略研究

杨 森，郭权利，李胜辉，杨宇昕，赵化锋

(1.沈阳工程学院，辽宁 沈阳 110136；2.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

专论

双馈风电场AVC系统协调优化控制策略研究

杨 森1，郭权利1，李胜辉2，杨宇昕1，赵化锋1

(1.沈阳工程学院，辽宁 沈阳 110136；2.国网辽宁省电力有限公司电力科学研究院，辽宁 沈阳 110006)

针对当前风电场AVC系统无功出力分配算法功能单一，无法实现风电场电压调节成本最低这一问题，提出了风电场AVC系统协调优化控制策略。该策略通过二阶震荡粒子群法对带有罚函数的风电场无功优化模型进行求解以降低风电场有功损耗，并通过调整无功源的工作方式实现电网电压的稳定。以辽宁地区某风电场为例，建立了该风电场的优化计算模型和包含所提控制策略的仿真模型。仿真结果表明，该策略可在保证风电场并网点电压稳定的同时，有效减小风电场稳态运行过程中的有功损耗，并在电网发生故障时为电网提供一定的无功支撑。

风电场AVC系统；罚函数；二阶震荡粒子群法

风电场自动电压控制(automatic voltage control，AVC)系统是风电场加强自身运行安全性及电压稳定性的关键技术[1]。其控制目标是通过调节成本最小的方式使公共连接点(PCC)电压稳定在要求范围。目前国内外学者关于AVC系统控制策略的研究多集中于稳定风电场PCC点电压。如文献[2]中推导出了适用于风电场AVC系统的分区图简化策略，为风电场无功设备的协调优化提供了一种实用化的方法；文献[3]提出的风电系统无功功率实时协调控制策略，可在稳态运行时有效抑制风电场的无功功率波动，提高风电场PCC点电压稳定性；文献[4]在风电场AVC系统中引入了风功率预测信息，并在此基础上建立了包含风电场计划、在线、紧急模式的多层动静态电压协调控制模型。

在实际运行中，AVC系统在我国风电场中的应用尚未成熟，缺乏统一的设计规范，不同地区的控制策略不尽相同[5-7]。如辽宁地区的风电场AVC系统控制策略采用等功率因数分配策略分配各风电机组的无功出力值，当机组无功出力不足投入动态无功补偿装置进行快速调节。此种控制策略虽能保证风电场PCC点的电压稳定在要求范围内，但无法保证风电场处于最经济的运行状态。

结合当前AVC系统存在的问题以及目前的研究现状，本文提出了风电场AVC系统的协调优化控制策略。

1 无功协调优化控制策略

1.1 风电场主要无功源

目前我国双馈风电场中主要的无功源有SVC、SVG和双馈风力发电机(DFIG)。SVC和SVG具有响应速度快且无功容量较大的特点，故在风电场中常作为动态无功补偿装置使用，但由于其损耗较大，多用于暂态调节或作为无功备用。DFIG本身具有较大的无功容量且能够自由调节，其无功出力受AVC系统的控制。但由于AVC系统需要在通信过程中花费较多时间，因此DFIG的无功调节速度较慢，一般为秒级，而电网的暂态过程为毫秒级。所以DFIG只能用于稳态调节，而无法用于暂态调节。

1.2 稳态控制模式

为了保证风电场经济运行，同时为了避免多个无功源在完成同一补偿任务时出现相互冲突的情况，当风电场稳态运行时，以AVC系统为主控系统，协调控制风电场内所有具有无功能力的DFIG及动态无功补偿装置。

当电网下达风电场PCC点电压要求时，AVC系统根据PCC点电压、电流、功率因数的测量值以及PCC点功率因数角参考值等按式(1)计算出当前风电场的无功出力参考值，若此时风电场内DFIG无功出力上限大于该值，则AVC系统令风电场内具有无功能力的DFIG中无功裕度最大的1台(假设为第m台)工作于恒电压模式(电压参考值设定为UN)，其余DFIG工作于恒无功模式，由AVC系统经优化计算得到无功出力值(无功出力约束由式(2)计算得到)。若DFIG无功出力总上限小于该值，则先将DFIG切换至恒无功模式，AVC系统对所有具有无功能力DFIG下达最大无功出力命令，之后投入动态无功补偿装置并使其工作于恒电压模式。具体控制逻辑如图1所示。

Qref=UsIscosφstanφref

(1)

式中：Us为PCC点电压测量值；Is为PCC点电流测量值；cosφs为PCC点功率因数测量值；φref为PCC点功率因数角参考值，此值由给定的功率因数参考值cosφref求得。

Qw1+Qw2+…+Qw(m-1)+Qw(m+1)+…+Qwn

(2)

式中：Qwi(i=1，2,…，m-1,m+1,…，n)为第i台DFIG的无功出力参考值；Qwm max为无功裕度最大的DFIG的无功出力上限；Qref为根据式(1)计算得到的风电场无功出力参考值。

1.3 暂态控制模式

根据上文的论述可知，动态无功补偿装置是暂态过程中风电场内唯一可调的无功源。因此，当检测到风电场PCC点电压越限时，置脱离AVC系统控制，并切换至恒电压模式，通过场内闭环控制模式控制PCC点电压。当检测到PCC点电压恢复到正常范围时，动态无功补偿装置保持当前状态，并准备接收AVC系统指令，AVC系统则根据当前电网调度指令按稳态模式运行。控制策略具体如图2所示。

动态无功补偿装

图2 暂态控制策略逻辑框图

2 计及动态无功补偿装置的风电场无功优化模型

2.1 无功优化模型的建立

a.目标函数

为达到在满足电网无功需求的前提下降低风电场损耗的目的，本文将以风电场有功损耗最小作为目标函数。计算风电场有功损耗时，计及DFIG损耗、线路损耗、变压器损耗以及动态无功补偿装置的损耗。目标函数：

min∑PG+PT+PL+Ploss

(3)

式中：PG为风电场全部处于运行状态的DFIG有功损耗；PT为风电场所有运行中变压器的有功损耗；PL为风电场输电线路的有功损耗；Ploss为动态无功补偿装置的有功损耗。

b.约束条件

潮流约束条件：

(4)

式中：PGi、QGi分别为节点i的有功、无功发电功率；PLi、QLi分别为节点i的有功、无功负荷功率；Ui、Uj为节点i、j的电压幅值；Gij、Bij、δij分别为支路ij的电导、电纳和节点i、j之间的相角差。

不等式约束条件：

(5)

式中：PG、QG为机组的有功和无功出力；UPCC为风电场PCC点电压；C为并联电容器投切容量；T为有载调压变压器分接头位置；cosφ为DFIG的功率因数。

风电场无功出力等式约束条件：等式约束条件如式(2)所示。

c.增广目标函数

为了提高优化模型的运算效率，本文将以罚函数的形式对目标函数和无功出力等式约束条件进行处理，处理后的增广目标函数：

(6)

式中：rk为罚因子，c为缩小系数。

2.2 无功优化模型的求解

标准粒子群优化(PSO)算法易陷入局部最优解，为了改善算法的局部收敛性，本文采用二阶震荡粒子群算法对无功优化模型进行求解。

算法流程如下。

步骤1：输入DFIG、线路、变压器、动态无功补偿装置的相关参数，当前处于运行状态的DFIG的运行数据，测得的实时风电场潮流数据。

步骤2：设置收敛条件及最大迭代次数。

步骤3：对粒子群维数、位置、速度、个体最优解和全局最优解进行初始化。

步骤4：由式(6)计算每一粒子的适应度值。

步骤5：将每一粒子的适应度值与该粒子当前的个体最优解进行比较，若适应度值小于个体最优解，则将该粒子的适应度值赋值给个体最优解。

步骤6：从整个粒子群中找到最小的个体最优解，将该个体最优解同群体最优解进行比较，若个体最优解小于群体最优解，则将个体最优解的值赋值给群体最优解，反之则保持不变。

步骤7：按式(7)和式(8)更新每一粒子的速度与位置。在更新完成后检查粒子位置是否越限，若越限则将越限的粒子位置用其最大(最小)约束值代替。

vi,j(t+1)=ωvi,j(t)+c1r1[pi,j-(1+ξ1)xi,j(t)+ξ1xi,j(t-1)]+c2r2[pg,j-(1+ξ2)xi,j(t)+ξ2xi,j(t-1)]

(7)

xi,j(t+1)=xi,j(t)+vi,j(t+1)

(8)

其中，若当前进化代数小于最大进化代数的一半时，取：

(9)

若当前进化代数大于最大进化代数的一半时，取

(10)

步骤8：当迭代结果满足误差要求或循环次数达到最大时终止计算，否则调回步骤4。

3 算例分析

为了验证优化算法是否能够降低风电场有功损耗提高运行经济性，根据上文所述的风电场建模方法及辽宁地区某风电场相关设备的数据，在MATLAB中编写了带有罚函数的二阶震荡粒子群法的风电场无功优化程序。并编写了等功率因数分配DFIG无功出力的风电场损耗计算程序与之进行对比。程序中风电场内的所有DFIG的有功出力均设为额定值，功率因数取±0.95。计算结果如图3所示。

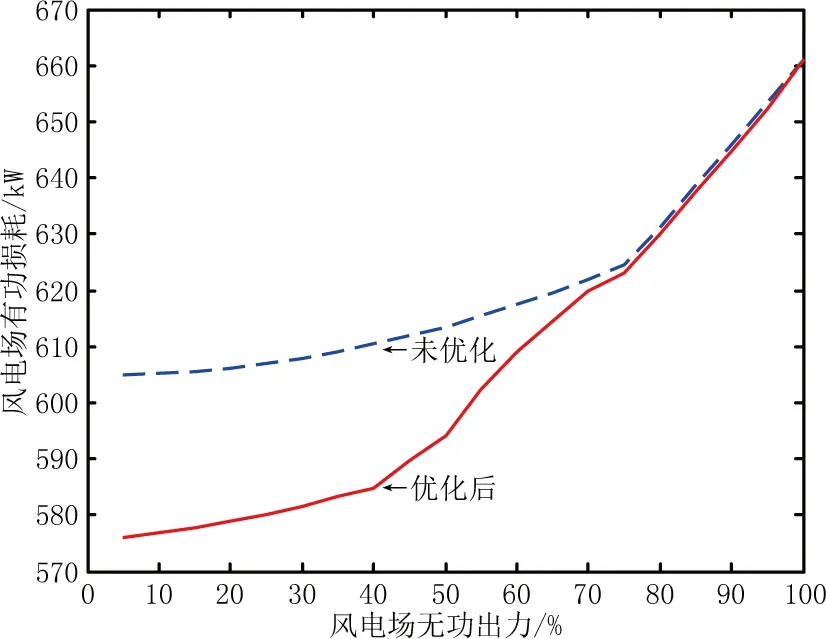
图3 优化前后风电场有功损耗

从图3中可以看出，当风电场无功出力低于75%时，优化后的损耗较未优化时的损耗小很多，而当无功出力大于75%时，优化效果则并不明显，但也小于未进行优化的结果。

为了验证本文所提控制策略能够保证风电场的稳定运行，本文以辽宁地区某风电场为例，在SIMULINK中搭建了该风电场的离散仿真模型。风电场由31台1.5 MW的DFIG及1台5 Mvar的SVG组成，接入66 kV电网中。风速设为12±1 m/s，66 kV系统短路容量设为1 050 MVA。将本文所提控制策略加入仿真模型中。风电场PCC点电压有效值的仿真波形如图4所示。

通过图4的电压波形可以看出，在稳态运行过程中说明本文所提的稳态控制策略可以保证风电场的正常运行。结合上文所述的优化算法仿真结果，可以证明本文所提的稳态优化控制策略的有效性。

通过设置66 kV电网电压三相电压跌落至85%来模拟电网故障，故障时间设为300 ms。电压跌落时风电场PCC点电压有效值(pu)仿真波形如图5所示。图5中，虚线为未使用本文所提暂态控制策略时风电场PCC点电压波形，实线为使用本文所提暂态控制策略后的电压波形。从图5中可以看出，当电网由于故障出现电压跌落时，系统电压的最低值由之前86%上升至88%，说明本文所提的暂态控制策略可以在暂态过程中为电网提供一定的电压支撑，能够在一定程度内减轻暂态过程对电网稳定的危害。

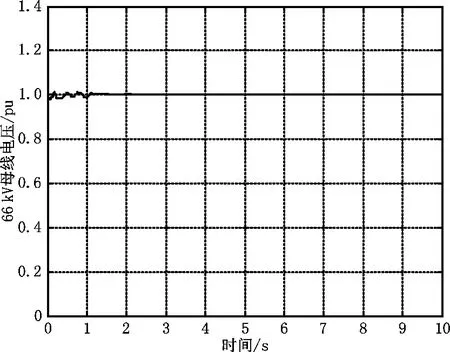
图4 风电场PCC点电压仿真波形

4 结论

根据风电场内不同无功源的响应速度及现场实际情况提出了风电场AVC系统的协调优化控制策略，在策略中建立了包含罚函数的无功优化模型，并利用二阶震荡粒子群法对其进行了求解。仿真结果表明，本文提出的优化控制策略可以在保证风电场正常运行的前提下 有效降低风电场稳态运行过程中的有功损耗，并在电网发生故障时对电网进行无功支撑，提升了暂态过程的PCC点电压，降低了暂态过程对风电场及电网的危害。

[1] 乔 颖，陈惠粉，鲁宗相，等.双馈风电场自动电压控制系统设计及应用[J].电力系统自动化，2013，37(5)：15-22.

[2] 乔 颖，鲁宗相，徐 飞.双馈风电场自动电压协调控制策略[J].电力系统自动化，2010，34(5)：96-101.

[3] 王成福.风电场并入电网的调控理论研究[D].济南：山东大学，2012.

[4] 张乐丰.风电场风机有功、无功协调优化调度研究[D].北京：华北电力大学，2015.

[5] 赵晶晶，符 杨，李东东.考虑双馈电机风电场无功调节能力的配电网无功优化[J].电力系统自动化，2011，35(11)：33-38.

[6] 陈 蕊，夏安邦，马玉龙.电力系统无功优化算法综述[J].东北电力技术，2006，27(6)：38-41.

[7] 许睿超，罗卫华.大规模风电并网对电网的影响及抑制措施研究[J].东北电力技术，2011，32(2)：1-4.

Research on Coordinating Control Strategy of AVC System in DFIG Based Wind Farm

YANG Sen1,GUO Quanli1,LI Shenghui2,YANG Yuxin1,ZHAO Huafeng1

(1.Shenyang Institute of Engineering,Shenyang,Liaoning 110136,China;2.Electric Power Research Institute of State Grid Liaoning Electric Power Co.,Ltd.,Shenyang,Liaoning 110006,China)

The function of distributing reactive power algorithm is single.The AVC system of wind farm can’t reduce the cost of regulating voltage.To rich arithmetic functions,this paper presents a coordinating control strategy.This strategy uses the second-order oscillation particle swarm optimization to solve theoptimization model with penalty function which can reduce the loss of wind farm.Steady voltage is realized by adjusting the work methods of reactive power sources.Given wind farm in Liaoning is taken as the research object in this study,optimization and simulation model with the strategy is established.The simulation results show that this streategy can reduce the active loss and decrease the damage to the power grid.

wind farm AVC system;penalty function;second-order oscillation particle swarm

TM614

A

1004-7913(2017)01-0001-04

杨 森(1992)，男，在读硕士，研究方向为风电场无功优化。

2016-09-30)