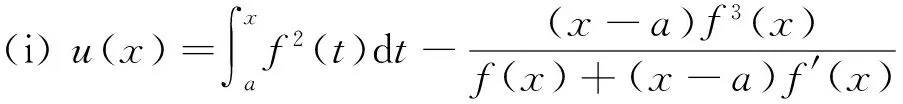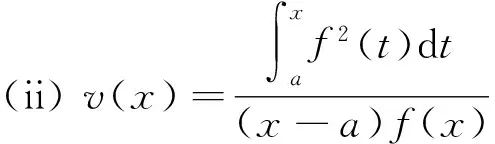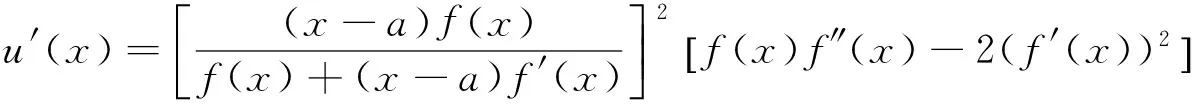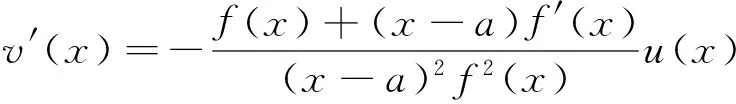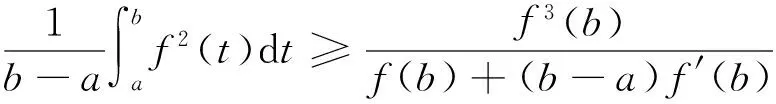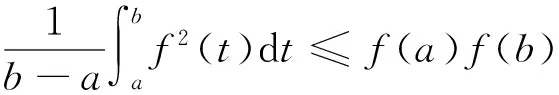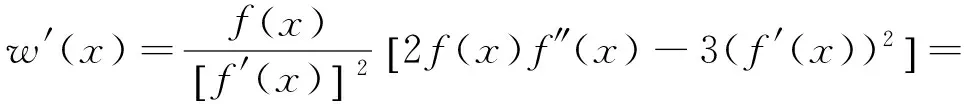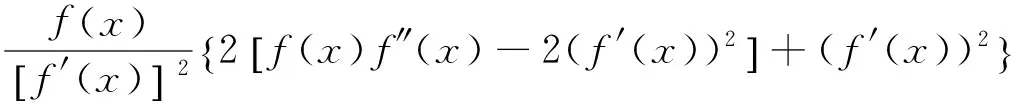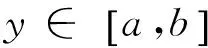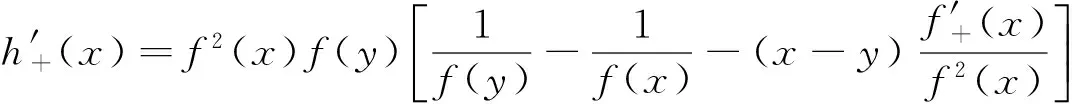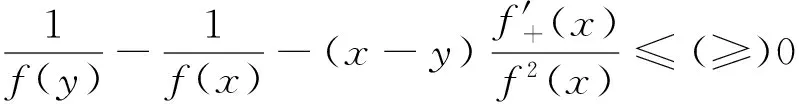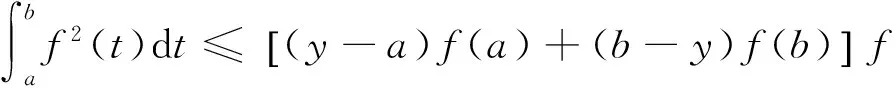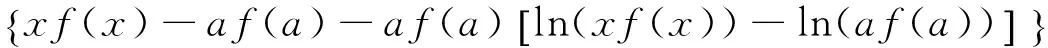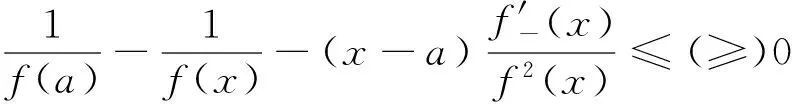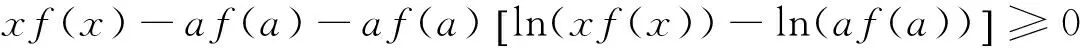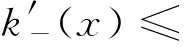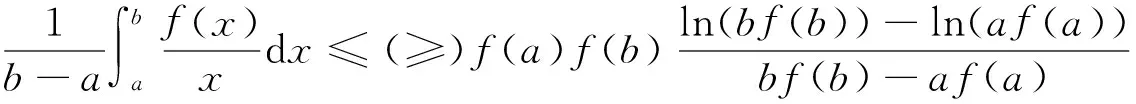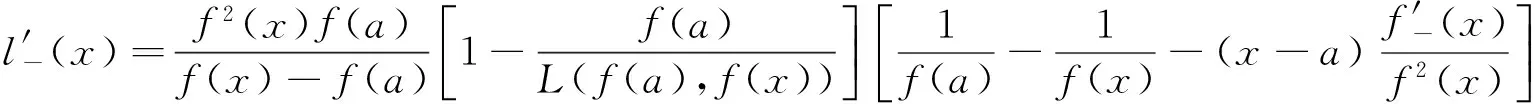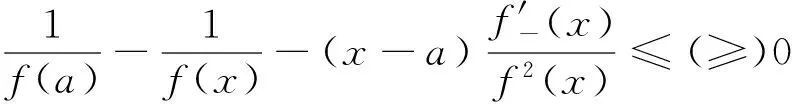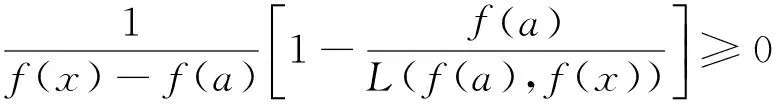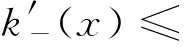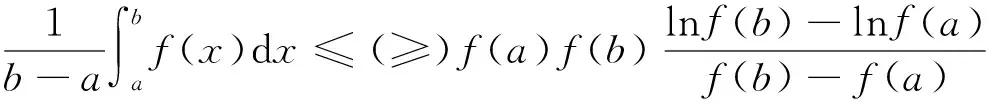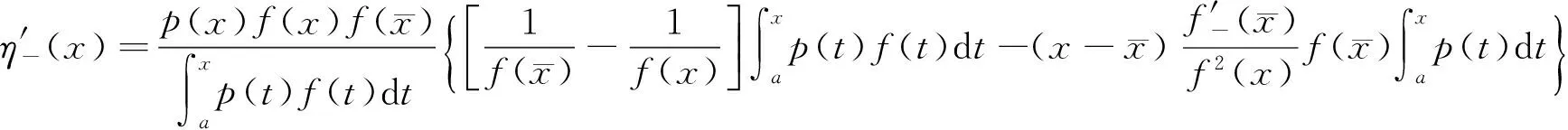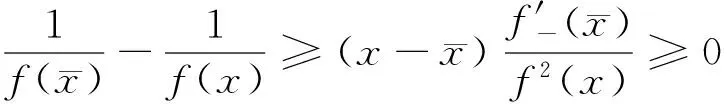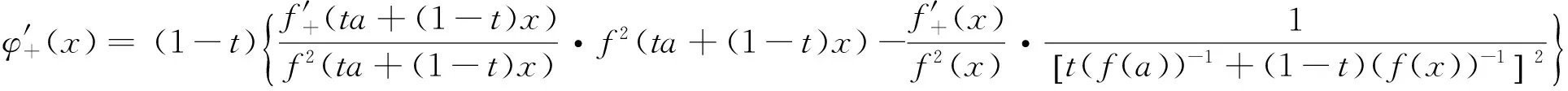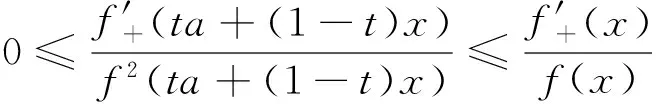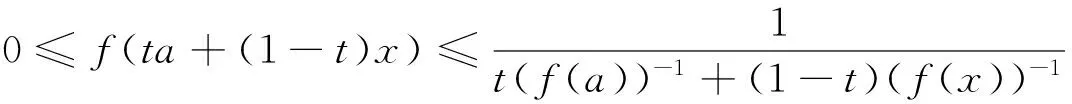与AH凸函数有关的若干单调函数
时统业, 秦 华, 王 斌
(1. 海军指挥学院信息系,江苏 南京 211800; 2. 海军蚌埠士官学校航海系,安徽 蚌埠 233012)
与AH凸函数有关的若干单调函数
时统业1, 秦 华1, 王 斌2
(1. 海军指挥学院信息系,江苏 南京 211800; 2. 海军蚌埠士官学校航海系,安徽 蚌埠 233012)
利用AH凸函数的定义和基本性质,证明了与AH凸函数有关的若干函数的单调性,并利用这些单调性定理,得到几个与AH凸函数有关的积分不等式.
AH凸函数;单调性;单侧导数
1 预备知识
定义1[1-2]设I⊆R,f:I→(0,+∞),若对任意x1,x2∈I和任意t∈[0,1],有
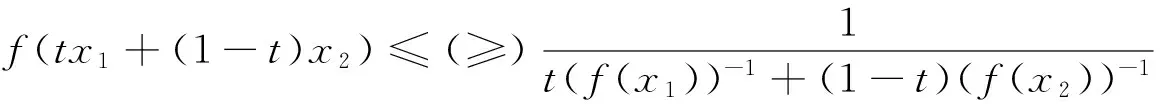
则称f(x)是区间I上的AH凸(凹)函数.
引理1[2]区间[a,b]上二阶可导正值函数f(x)为AH凸(凹)函数的充要条件是
2(f′(x))2-f(x)f″(x)≤(≥)0.
引理2[3]设f:[a,b]⊆R→(0,+∞)为AH凸(凹)函数,x,y∈(a,b),则
(i)f在(a,b)内任意点处的单侧导数存在;
(ii)若x 引理3 设f:[a,b]⊆(0,+∞)→(0,+∞)是AH凸函数,则 (i) (x-a)f(x)在(a,b)上严格单调增加; (ii) 若f在(a,b)上可导,则有f(x)+(x-a)f′(x)>0. 由此得(x1-a)f(x1)<(x2-a)f(x2),故证得(x-a)f(x)在(a,b)上严格单调增加. 引理4[3]设f:[a,b]⊆R→(0,+∞)是连续的AH凸(凹)函数,p(x)是正的可积函数,则 其中 定理1 设f:[a,b]⊆(0,+∞)→(0,+∞)是连续的AH凸函数,且在[a,b]上二阶可导,则 证明 (i)对任意x∈[a,b], 由引理1有f(x)f″(x)-2(f′(x))2≥0,于是在[a,b]上有u′(x)≥0,故u(x)在[a,b]上单调增加. (ii)对任意x∈(a,b], 由引理3有f(x)+(x-a)f′(x)>0,由(i)知u(x)>0,故在(a,b)上有v′(x)<0,因此v(x)在(a,b]上单调减少. 推论1 设条件同定理1,则有 (1) (2) 定理2 设f:[a,b]⊆(0,+∞)→(0,+∞)是二阶可导的AH凸函数,且严格单调,则函数 在[a,b]上的严格单调增加. 因f严格单调,故(f′(x))2>0,又由引理1有f(x)f″(x)-2(f′(x))2≥0,故w′(x)>0,即w(x)在[a,b]上严格单调增加. 推论2 设条件同定理2,则有 (3) 证明 由定理2有w(b)≥w(a),由此证得式(3). 推论3 设f:[a,b]⊆(0,+∞)→(0,+∞)是二阶可导的AH凸函数,且严格单调增加(减少),则函数 是[a,b]上的AH凸(凹)函数. 证明 因w(a)≤w(x),又当f在[a,b]上单调增加(减少)时有f′(x)>(<)0,故2(l′(x))2-l″(x)l(x)≤(≥)0,由引理1,f是[a,b]上的AH凸(凹)函数. 在[a,b]上单调减少(增加). 证明 对任意x∈(a,b), 推论4 设条件同定理3,则有 定理4 设f:[a,b]⊆(0,+∞)→(0,+∞)是连续的AH凸(凹)函数,且当x≠a时,有xf(x)≠af(a),则函数 在(a,b]上单调减少(增加). 证明 对任意x∈(a,b), 因为 推论5 设条件同定理4,则有 (4) 证明 由定理4有k(b)≤(≥)k(a),由此证得式(4). 定理5 设f:[a,b]⊆(0,+∞)→(0,+∞)是连续的AH凸(凹)函数,且当x≠a时,有f(x)≠f(a),则函数 在(a,b]上单调减少(增加). 证明 对任意x∈(a,b), 因为 推论6[6]设条件同定理5,则 (5) 证明 由定理5有l(b)≤(≥)l(a),由此证得式(5). 定理6 设f:[a,b]⊆(0,+∞)→(0,+∞)是连续的AH凸函数,且单调增加,p(x)是正的可积函数,则函数 在(a,b]上单调增加. 定理7 设f:[a,b]⊆(0,+∞)→(0,+∞)是连续的AH凸函数,且单调增加,t∈(0,1),则函数 在[a,b]上单调减少. 证明 对任意x∈(a,b), 因为x≥ta+(1-t)x,由引理2及f的单调增加性有 又由AH凸函数的定义得 [1] 张天宇,王淑红.关于算术调和凸函数的Hermite-Hadamard型不等式[J].内蒙古民族大学学报(自然科学版),2012,27(4):397-399. [2] 陈少元.AH-凸函数及其应用[J].湖北职业技术学院学报,2013,16(2):106-109. [3] 时统业,李照顺,秦华.与AH凸函数有关的若干积分不等式[J].杭州师范大学学报(自然科学版),2016,15(3):307-311. [4] 杨军.用单侧导数判断函数的单调性[J].四川师范学院学报(自然科学版),2000,21(1):108-109. [5] 李丹衡,邓远北.函数的左、右导数的应用[J].高等数学研究,1999,2(3):26-28. [6] 何晓红,许谦.AH凸函数的几个积分不等式及其应用[J].上海大学学报(自然科学版),2014,20(3):368-373. Some Monotone Functions Related to AH-convex Functions SHI Tongye1, QIN Hua1, WANG Bin2 (1. Department of Information, PLA Naval Command College, Nanjing 211800, China; 2. Department of Navigation,PLA Bengbu Naval Petty Officer Academy, Bengbu 233012, China) The monotonicity of several functions related to AH-convex functions are proved by means of the definition and basic properties for AH-convex functions, and sever integral inequalities for AH-convex functions are obtained by using these theorems. AH-convex function; monotonicity; unilateral derivative 2016-03-09 时统业(1963—),男,副教授,硕士,主要从事基础数学教学和研究.E-mail:shtycity@sina.com 10.3969/j.issn.1674-232X.2017.01.022 O178 MSC2010:26B25;26D15 A 1674-232X(2017)01-0103-05
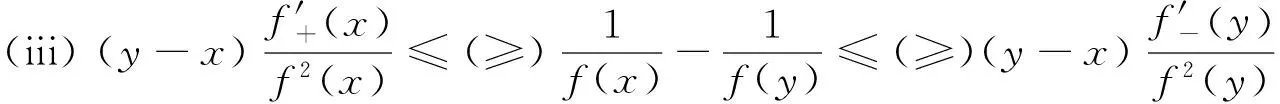
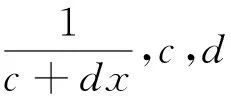
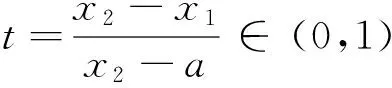
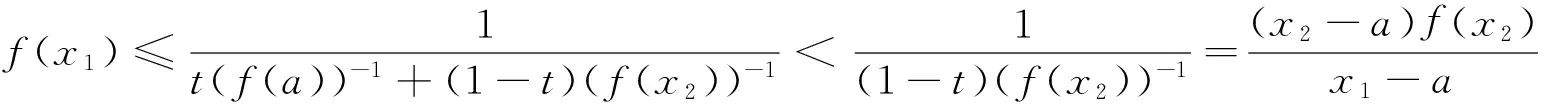
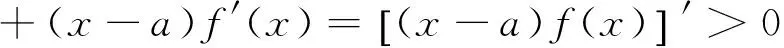

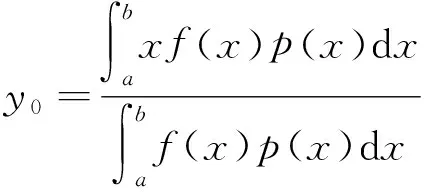
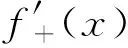
2 主要结果