振动频率法检测吊杆索力试验研究

江 聪 聪

(兰州交通大学土木工程学院，甘肃 兰州 730070)

振动频率法检测吊杆索力试验研究

江 聪 聪

(兰州交通大学土木工程学院，甘肃 兰州 730070)

介绍了振动频率法的基本原理，并利用振动频率法，对某悬索桥吊杆索力进行现场检测，检测结果与工程实际情况相符合，表明振动频率法能够保证吊杆索力测试的精度要求。

悬索桥，振动频率法，吊杆，索力，精度要求

1 工程概况

该悬索桥为180 m跨度的柔性吊桥，矢高为15 m，矢跨比为1/12，两侧主缆各由14根φ45 mm钢丝绳组成，桥面跨中原设计拱度0.92 m，其余各点按抛物线设计。全桥共设44对吊杆，上下游两侧对称布置，每一侧吊杆均沿由北岸至南岸依次为1号～44号吊杆，悬索桥立面图见图1。

2 检测原理及测点布置

2.1 检测原理

利用附着在吊杆上的高灵敏度加速度传感器拾取吊杆在环境激励或人工激励下的振动信号，经过滤波、放大和频谱分析，再由频谱图确定拉索的自振频率，最后根据频率与索力的关系确定索力[1]。

其结果的准确性关键在于吊杆索力与自振频率这两者之间关系的准确性。频率法测试吊杆索力的方法最早采用的是传统的弦振动理论，即忽略吊杆的抗弯刚度与边界条件对自振频率的影响，将吊杆当成一根拉紧的弦进行计算。此方法在测试索力时有其局限牲，因为其测量精度仅对较长的吊杆可以得到保证[2]。

2.2 测点布置

由于短吊杆的抗弯刚度对于固有频率的影响不可忽略，而且无论是采用两端固结模型还是两端铰支模型，最后求得的吊杆索力误差都比较大，因此对于短吊杆，假如使用传统的频率法来测试索力，由于此方法的局限性，最后将会产生很大的误差，故为保证测试的精确性，对该桥小于3 m的吊杆不采用振动频率法测试索力[3]。

测试采用INV信号采集分析仪和INV9808加速度传感器。传感器固定在上游侧吊杆距桥面约1.5 m位置处。加速度传感器安装见图2。

3 吊杆索力的现场测试

现场采用振动法测试吊杆的激振频率，根据频率与索力的关系计算出构件拉力，了解吊杆在恒载作用下的受力状况。检测时，考虑振动法测试条件要求，现场选取上游侧长度超过3 m的吊杆进行测试，吊杆索力测试见图3。

表1 吊杆拉力测试及分析结果

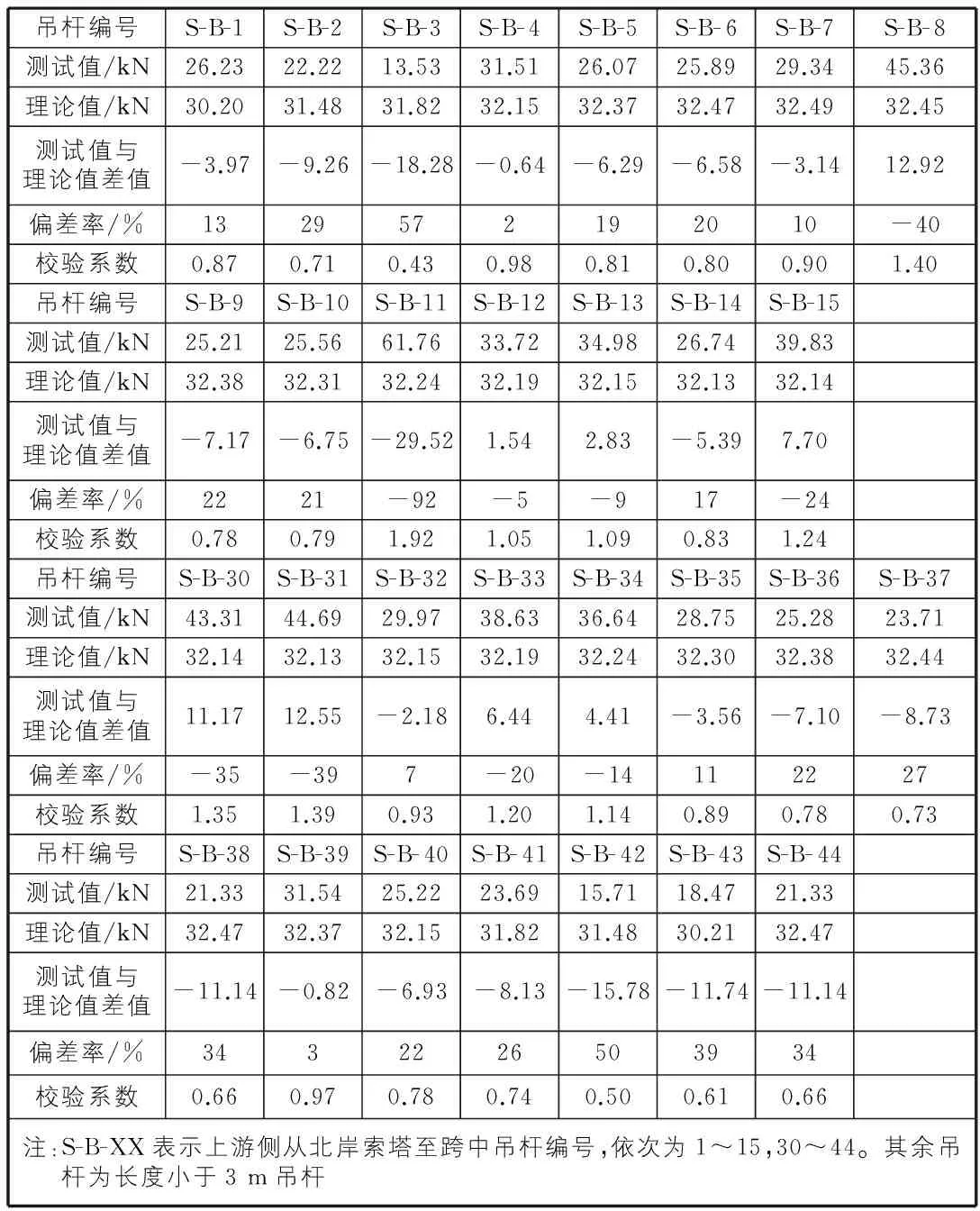
吊杆编号S-B-1S-B-2S-B-3S-B-4S-B-5S-B-6S-B-7S-B-8测试值/kN26.2322.2213.5331.5126.0725.8929.3445.36理论值/kN30.2031.4831.8232.1532.3732.4732.4932.45测试值与理论值差值-3.97-9.26-18.28-0.64-6.29-6.58-3.1412.92偏差率/%1329572192010-40校验系数0.870.710.430.980.810.800.901.40吊杆编号S-B-9S-B-10S-B-11S-B-12S-B-13S-B-14S-B-15测试值/kN25.2125.5661.7633.7234.9826.7439.83理论值/kN32.3832.3132.2432.1932.1532.1332.14测试值与理论值差值-7.17-6.75-29.521.542.83-5.397.70偏差率/%2221-92-5-917-24校验系数0.780.791.921.051.090.831.24吊杆编号S-B-30S-B-31S-B-32S-B-33S-B-34S-B-35S-B-36S-B-37测试值/kN43.3144.6929.9738.6336.6428.7525.2823.71理论值/kN32.1432.1332.1532.1932.2432.3032.3832.44测试值与理论值差值11.1712.55-2.186.444.41-3.56-7.10-8.73偏差率/%-35-397-20-14112227校验系数1.351.390.931.201.140.890.780.73吊杆编号S-B-38S-B-39S-B-40S-B-41S-B-42S-B-43S-B-44测试值/kN21.3331.5425.2223.6915.7118.4721.33理论值/kN32.4732.3732.1531.8231.4830.2132.47测试值与理论值差值-11.14-0.82-6.93-8.13-15.78-11.74-11.14偏差率/%3432226503934校验系数0.660.970.780.740.500.610.66注:S-B-XX表示上游侧从北岸索塔至跨中吊杆编号,依次为1～15,30～44。其余吊杆为长度小于3m吊杆

采用Midas Civil有限元分析软件建立有限元模型(见图4)，分析吊杆恒载作用下的吊杆索力。

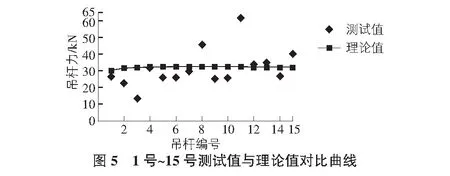
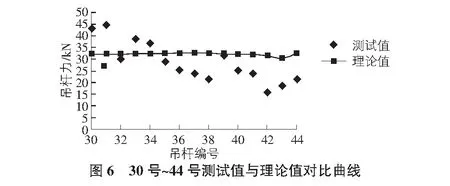
吊杆测试及理论分析结果见表1，图5，图6。

吊杆的部分测试时程曲线及频谱曲线见图7，图8。

从测试结果可见，1号，4号，5号，7号，12号～14号，32号，34号，35号，39号等吊杆的偏差率未超过20%，但其余吊杆拉力测试值与理论值偏离较大，吊杆在恒载状态时受力与计算值偏差较大。

4 结语

根据采集的振动频率测试吊杆的索力。通过测试数据与理论数据进行对比，结果基本上能满足精度要求。振动频率法测试简单、快捷，能较真实地测试出吊杆的索力。

[1] 冯东明，李爱群，李枝军，等.基于频率法的自锚式悬索桥吊索力测试与分析[J].东南大学学报，2009(S2)：106-110.

[2] 周科平.大型钢结构室内吊桥的吊杆索力测试分析参数优化研究[D].合肥：合肥工业大学，2015.

[3] 曾军伟.悬索桥吊杆张力分析与振动测试研究[D].重庆:重庆大学，2008.

On detection of suspender force test with vibration frequency method

Jiang Congcong

(CollegeofCivilEngineering,LanzhouJiaotongUniversity,Lanzhou730070,China)

The paper introduces the basic principle of the vibration frequency method, adopts the vibration frequency method to undertake the site detection of the suspender force of some suspension bridge, indicates the consistency between the tested results and the engineering circumstance, and proves the vibration frequency method can ensure the accurate demands for the test of the suspender force.

suspension bridge, vibration frequency method, suspender, cable force, accuracy requirement

1009-6825(2017)01-0189-03

2016-10-23

江聪聪(1993- )，男，在读硕士

U448.25

A