声波在电站锅炉含颗粒介质气体中的衰减特性

姜根山， 许伟龙， 安连锁

(1.华北电力大学 数理系，河北保定 071003；2.华北电力大学 能源动力与机械工程学院，北京 102206)

声波在电站锅炉含颗粒介质气体中的衰减特性

姜根山1， 许伟龙2， 安连锁2

(1.华北电力大学 数理系，河北保定 071003；2.华北电力大学 能源动力与机械工程学院，北京 102206)

采用数值计算方法研究了可听声频率范围内声波在电站锅炉炉膛中的衰减机理，建立了电站锅炉含颗粒介质气体中的声衰减系数计算公式，得到了声衰减系数与声频率、颗粒介质体积分数、颗粒粒径及烟气温度的关系.根据多体多次散射理论，对颗粒介质体积分数较大的循环流化床锅炉中的声波衰减特性进行了讨论，并对其声衰减系数进行了修正.结果表明：对于一般燃煤锅炉，随着烟气温度的升高以及颗粒介质体积分数和声频率的增大，声衰减系数增大，随着颗粒粒径的增大，声衰减系数减小；循环流化床锅炉中的声波衰减主要来源于颗粒介质表面的热传导耗散.

电站锅炉； 声传播特性； 声衰减系数； 多体多次散射理论

近年来，将声学技术应用于电站设备状态监测与控制已经受到广泛的关注及研究，如炉内声源(炉管泄漏源)的检测与定位，炉内温度场、流场和声场等物理量场的测量，炉内声波除灰以及声波助燃等技术[1-4].这些技术均涉及到炉内声传播特性，其作为理论基础对研究声学应用技术起着至关重要的作用.电站锅炉炉膛中环境复杂多变，煤粉随一次风喷入炉膛中进行燃烧，颗粒进入炉膛后随机分布在燃烧层，煤粉燃尽之后产生的飞灰也会随机分布在炉膛中，因此声波在炉膛含颗粒介质气体中的传播是一个十分复杂的问题，之前笔者研究了强声波在电站锅炉炉膛中的传播特性，然而并未考虑颗粒介质的影响.

针对颗粒介质中的声波衰减理论，最早Stokes[5]以水中的钟摆为模型研究了作用在小球上的黏滞力.Rayleigh研究了小颗粒对光波的散射，提出了散射截面反比于波长四次方的长波散射理论.Sewell[6]研究了黏滞流体中不动球形硬粒子的声波衰减特性，并对Rayleigh的结果进行了修正.而Lamb[7]则研究了黏滞流体中可自由运动球形硬粒子的声波衰减特性.然而，以上理论仅在颗粒介质体积分数很小时才成立，当其体积分数接近于0.1或更大时，实验结果与理论结果相差很大[8].Allegra等[9]联立质量守恒、动量守恒和能量守恒方程求出考虑粒子散射、黏滞及热传导效应时的声吸收系数，给出了考虑声吸收因素最为全面的理论.Sheng等[10]根据Johnson提出的高通模型，建立了球形粒子散射衰减系数的高通模型表达式，该式也是目前计算散射衰减系数的通用表达式.钱祖文[11]以海洋浅层沉积和液体中的气泡为例，采用多体多次散射理论研究了高浓度颗粒介质中的声传播特性.杨文泽[12]在冷态工况下初步测试了气固两相流介质中的声波衰减特性.Valverde[13]研究了强声波的声流效应对循环流化床锅炉炉膛中颗粒的影响，分析了强声波在循环流化床锅炉中的衰减特性.目前，颗粒介质中声传播特性研究主要集中在水声学或气液两相流中，有关气固的研究相对较少，且所研究的声波多集中在高频段，对于可听声频率范围内的声波在颗粒介质中衰减特性的研究十分缺乏.

结合电站锅炉炉膛中的实际情况，笔者分析了可听声频率范围内的声波在炉膛中的衰减机理，研究了衰减机理与声频率、颗粒介质体积分数、烟气温度和颗粒粒径的关系，给出了炉膛中声衰减系数计算公式，并根据多体多次散射理论对颗粒介质体积分数较大的循环流化床锅炉中的声衰减系数进行了讨论和修正.

1 颗粒介质间无相互作用时声波的衰减特性

若某种流体中出现物理性质不同的其他颗粒物时，将其称为颗粒介质(或悬浮流体).当颗粒物的体积分数很小，以至于颗粒之间的相互作用可以忽略时，可将其称为低浓度颗粒介质(或稀悬浮流体)，否则称为高浓度颗粒介质(或浓悬浮流体)[14].

1.1 媒质的黏滞吸收和热传导吸收

在可听声频率范围内，媒质的弛豫效应可以忽略，根据声吸收的经典公式可以得到声吸收系数

(1)

式中：αf为媒质的声吸收系数；ω为振荡角频率；ρ为媒质的密度；c为媒质的声速；μ为切变黏滞系数；μ′为容变黏滞系数，一般情况下在可听声频率范围内，μ′可以忽略；λ为热传导系数；cp为比定压热容；cv为比定容热容.

电站锅炉炉膛中烟气的声吸收系数为

(2)

从式(2)可以发现，媒质的声吸收系数与其物理性质有关，表1给出了炉膛压力为101 225 Pa(即负压为100 Pa)时烟气的物性参数，其中T和ν为烟气温度和运动黏度.

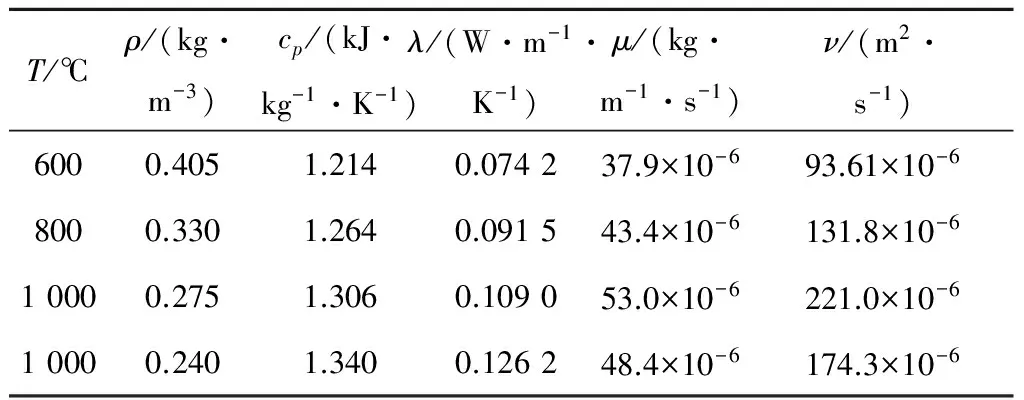
表1 烟气的物性参数

图1给出了不同烟气温度下声吸收系数随声频率f的变化.从图1可以看出，相同烟气温度下，声吸收系数随着声频率的增大而变大；相同声频率下，烟气温度越高，声吸收系数越大.从图1还可以看出，烟气温度的变化对声吸收系数的影响并不大.

1.2 颗粒介质对声波衰减特性的影响

声波在颗粒介质中的衰减主要包括颗粒表面热传导耗散、颗粒对媒质作相对运动的摩擦损耗(黏滞衰减)以及声波对粒子的散射引起的附加能量耗散，同时颗粒自激产生的声波也会影响其衰减特性[13].

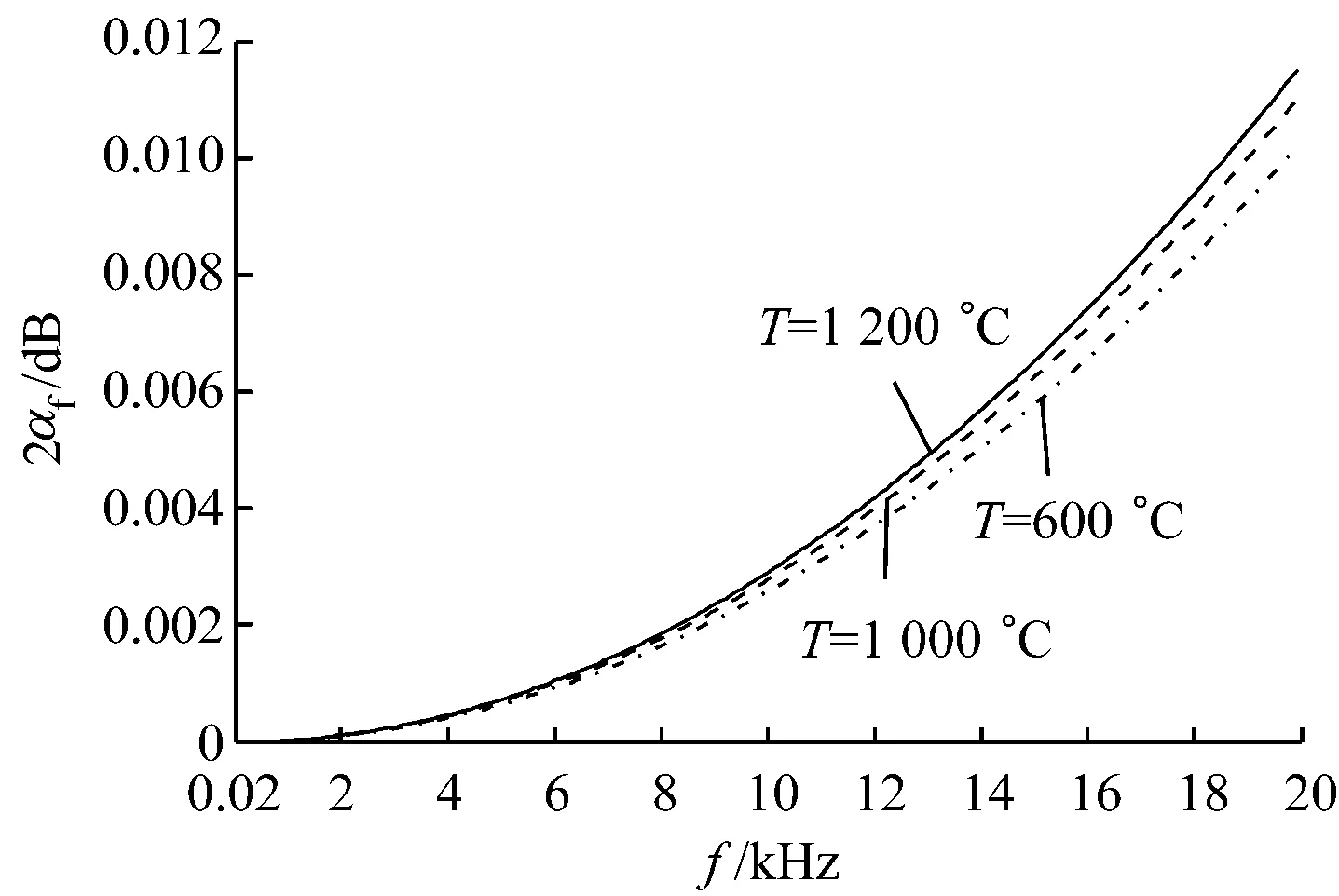
图1 不同烟气温度下声吸收系数随声频率的变化

1.2.1 颗粒自激作用及颗粒表面热传导耗散

炉膛中燃烧的煤粉颗粒温度远高于周围烟气温度，两者的温度梯度使得热量从煤粉颗粒流向烟气，发生热量交换即热传导，煤粉颗粒表面不可逆的热传导过程会引起声波的耗散.

假设煤粉颗粒为刚性球形颗粒，则半径为R的颗粒声吸收有效截面积σ为

(3)

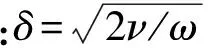
若单位体积内有N个这样的颗粒，则由单位体积内颗粒表面热传导引起的声衰减系数αa为

(4)

式中：N=3φ/(4πR3)，φ为煤粉在烟气中的体积分数.

从式(4)可以看出，颗粒表面热传导引起的声衰减系数与颗粒介质体积分数、颗粒粒径、声频率以及烟气的物性参数有关.

1.2.2 颗粒介质中的黏滞衰减和散射衰减

在颗粒介质中，颗粒介质会引起声波的散射；而在黏性流体中，颗粒的声散射场除了散射波外还会产生黏滞波.假设入射波是平面波，表达式为φi=eikZ，Z为入射波的传播方向，为了简化问题，假设入射波振幅为1，则有:

(5)

式中：k为波数，k=ω/c；r为到球心的距离；jn(kr)为n阶球贝塞尔函数；Pn(cosθ)为勒让德多项式；θ为入射角度.

散射的分离变量解可表示为

(6)

式中：An,1为第一次散射解的第n阶展开系数，由边界条件确定；hn(kr)为n阶汉克函数.

对于黏滞波，取矢量势A，有A=(Ar,Aθ,Aϑ),由于方位对称，Ar=0，Aθ=0，所以矢量势A=(0,0,Aϑ).分离变量并展开Aϑ，若省去下标，可得

(7)

式中：Cn,1为待定系数.

根据文献[13]，当kR<<1时有:

(8)

(9)

(10)

在电站锅炉炉膛中，颗粒粒径大约为100 μm且m>>1，而在可听声频率范围内，又有z<1，因此式(10)可以简化为

(11)

若在单位体积的流体中存在N个颗粒，颗粒之间无相互作用，耗散函数为

(12)

式中：Re(·)表示求实部.

入射波声强为

(13)

由此可得，相应的声衰减系数为

(14)

当kR<<1时，An,1中仅有n=0、1时为有限值，n>2时An,1为高阶无穷小，因此式(14)可以简化为

(15)

通过式(15)即可得到颗粒介质中黏滞衰减系数和散射衰减系数.

根据瑞利散射，单位体积内有N个小颗粒的理想流体中的散射衰减系数为

(16)

对于电站锅炉炉膛中煤粉颗粒的粒径范围以及可听声频率范围，根据式(11)和式(16)，进一步简化式(15)可得

(17)

式(17)等号右边第一项为声波黏滞衰减系数，第二项为声波散射衰减系数.

根据式(17)可以发现在电站锅炉炉膛中，在可听声频率范围内，声波的黏滞衰减系数要远大于散射衰减系数.

1.3 颗粒介质中的声衰减系数

电站锅炉中声衰减系数为

(18)

为了研究声衰减系数的相关性，引入穿透深度d10，d10=10/(2α),即为声波声强减少10 dB所需要的距离.

图2给出了烟气温度为1 200 ℃、颗粒粒径为100 μm时，不同颗粒介质体积分数下穿透深度随声频率的变化.从图2可以看出，在可听声频率范围内，颗粒介质体积分数越大，穿透深度越小，即声衰减系数越大；颗粒介质体积分数相同时，穿透深度随着声频率的增大而减小，即声衰减系数增大.这是因为颗粒介质体积分数越大，颗粒数目相应增加，黏滞衰减以及颗粒表面热传导耗散相应变大.而声频率越大，声波的波长越小，越容易衰减.

图3给出了烟气温度为1 200 ℃、颗粒介质体积分数为0.2时，不同声频率下穿透深度随颗粒粒径的变化.从图3可以看出，当烟气温度和颗粒介质体积分数一定时，随着颗粒粒径的增大(仍然需要满足kR<<1)，穿透深度增大，即声衰减系数减小；而当颗粒粒径一定时，声频率越大，穿透深度越小，即声衰减系数越大.这是因为随着颗粒粒径的增大，相同颗粒介质体积分数下颗粒数目减少，颗粒表面热传导耗散及黏滞衰减会相应减小，从而导致声衰减系数减小.

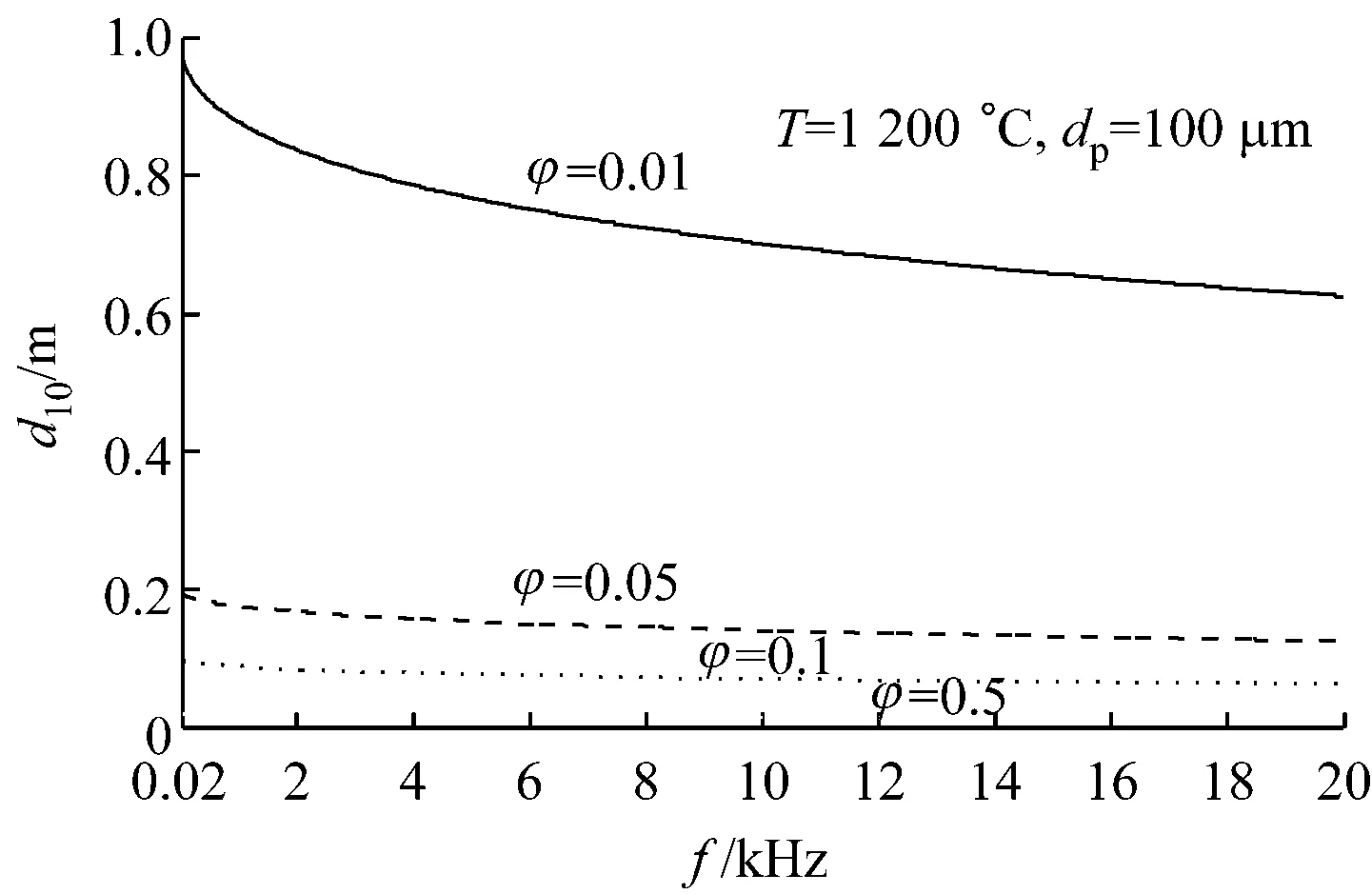
图2 不同颗粒介质体积分数下穿透深度随声频率的变化

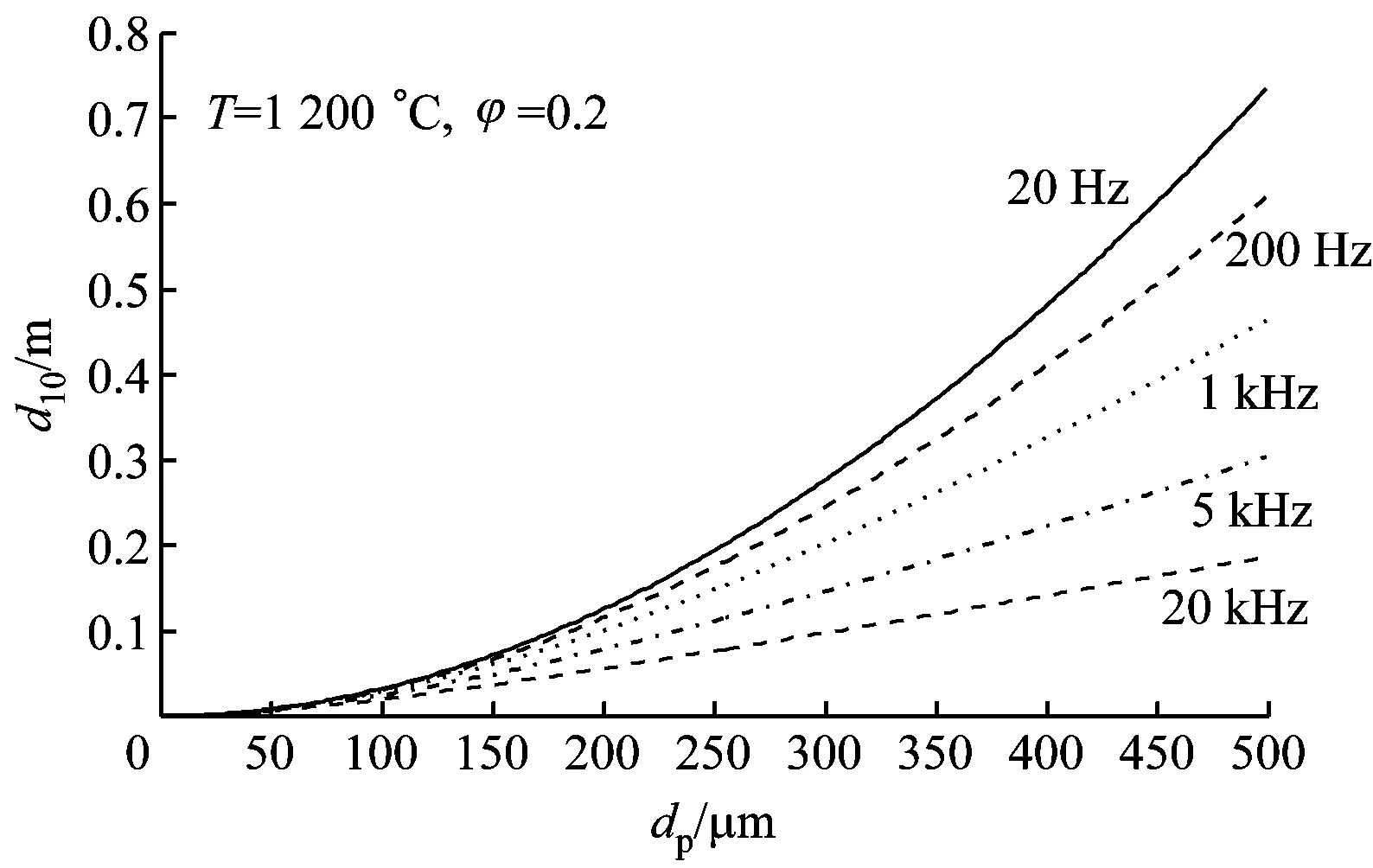
图3 不同声频率下穿透深度随颗粒粒径的变化

图4给出了烟气温度为1 200 ℃、颗粒粒径为100 μm时，穿透深度与声频率和颗粒介质体积分数的关系.

图4 不同声频率下穿透深度随颗粒介质体积分数的变化

图5(a)给出了声频率为5 kHz、颗粒介质体积分数为0.1时，穿透深度与烟气温度和颗粒粒径的关系.从图5(a)可以看出，颗粒粒径相同时，烟气温度越高，穿透深度越小，即声衰减系数越大.图5(b)给出了声频率为5 kHz、颗粒粒径为100 μm时，穿透深度与烟气温度和颗粒介质体积分数的关系.从图5(b)可以看出，当颗粒介质体积分数相同时，烟气温度越高，穿透深度越小，即声衰减系数越大.图5(c)给出了颗粒介质体积分数为0.1、颗粒粒径为100 μm时，穿透深度与烟气温度和声频率的关系.从图5(c)可以看出，当声频率保持不变时，烟气温度越高，穿透深度越小，即声衰减系数越大.综上分析，烟气温度升高，穿透深度减小，声衰减系数增大，这主要是因为随着烟气温度的升高，烟气中的气体分子运动更加活跃，增加了颗粒表面的热传导耗散、黏滞衰减以及媒质的声吸收，使得声衰减系数增大.

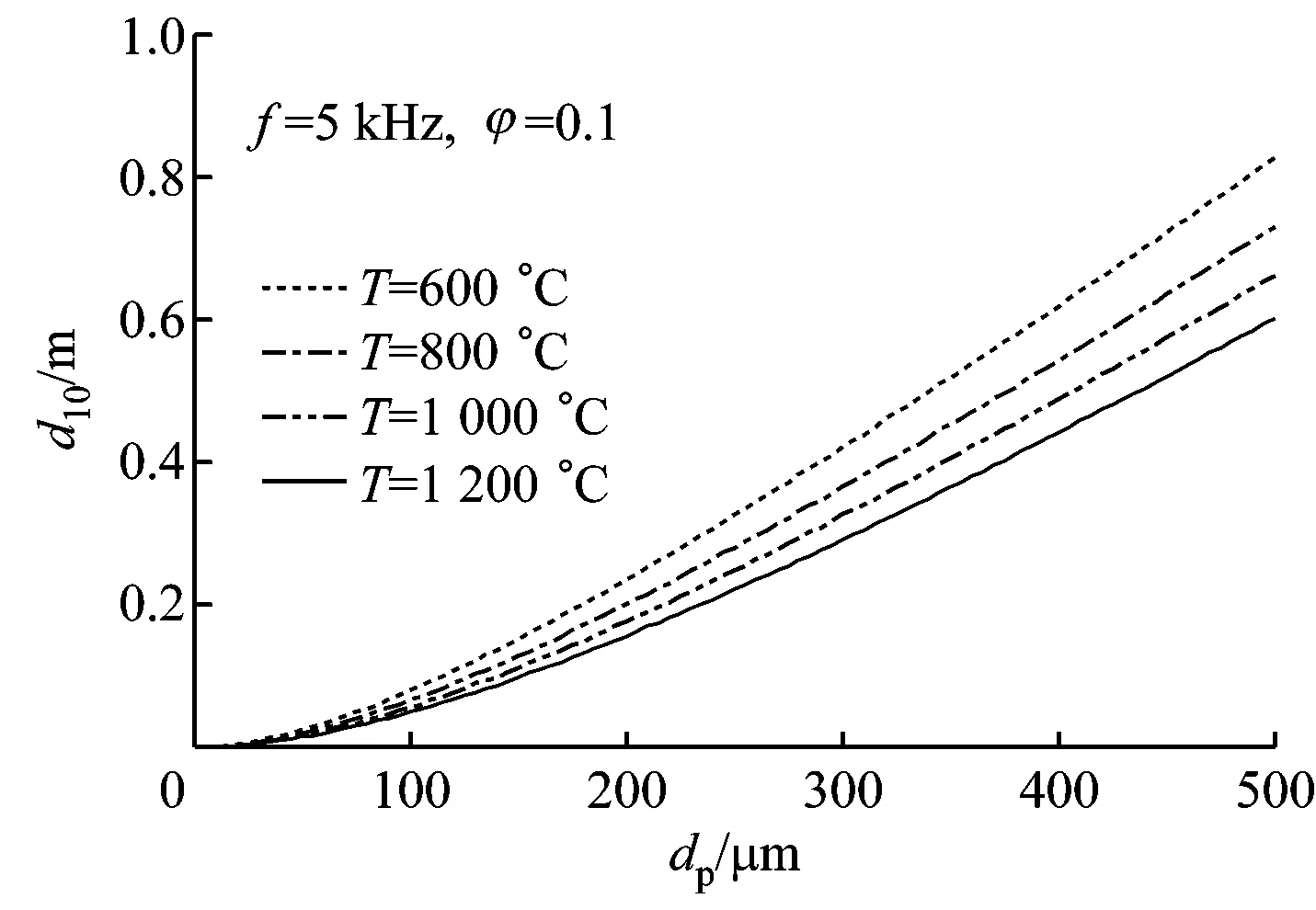
(a)

(b)

(c)

综上分析，由于电站锅炉炉膛中煤粉颗粒粒径在100 μm量级范围且所研究的声波在可听声频率范围内，根据式(18)可以发现，颗粒介质中声波衰减机理主要是由黏滞衰减以及颗粒表面热传导耗散引起的，而由煤粉颗粒引起的散射衰减以及媒质的黏滞吸收和热传导吸收几乎可以忽略.当不考虑烟气温度变化时，以上声波衰减变化规律与实验结果吻合[12].

2 颗粒介质间有相互作用时声波的衰减特性

通常燃煤锅炉炉膛中颗粒介质体积分数很小，而循环流化床锅炉对于炉膛中颗粒介质的体积分数一般在0.1～0.5，颗粒之间的相互作用不能忽略，采用多体多次散射理论研究循环流化床锅炉中高浓度颗粒介质的声波衰减特性.

2.1 散射波相互作用的颗粒介质中的声波衰减特性

当一列平面波在单位体积中有N个颗粒的流体中传播时，颗粒构成了声场中的散射体，任何颗粒除了受到原始入射波(平面波)的作用外，还受到其他颗粒在其所在处产生的次级场作用，将这2部分场称为该颗粒的等效入射场.根据多体多次散射理论，一列平面波沿x轴方向入射到颗粒介质中，P点为介质中某一颗粒所在位置，(rO，θO)为P点的极坐标；s为另一散射体，(rOs，θOs)为s点的极坐标；P点相对于s点的极坐标为(rs，θs)，则P点的原始入射波为

(19)

根据式(19)可以发现，此时入射波的振幅不再等于1，而是等于eikrOscos θOs.经过第一次多体散射后，P点的第二次等效入射场为原始入射场与第一次多体散射场之和:

(20)

由于kR<<1，散射场仅需取零阶和一阶量，φ0,1(P)和φ1,1(P)分别为P点处的零阶散射场和一阶散射场:

(21)

根据式(19)和式(21)，式(20)可以改写为

奶牛春秋两季配种受胎率最高，而夏季最低，这是由于热应激影响精子的成熟和精液成分，造成公牛性欲低下。另外，影响母牛卵细胞的分化、发育、着床，发情频率明显下降。

(22)

式中：W=γ0A0,1+γ1A1,1.

考虑多体n次散射，则P点的第n次等效入射场为

(23)

因此,考虑了多体多次散射相互作用后，散射衰减系数为

(24)

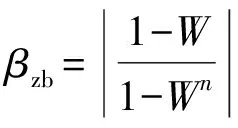
图6给出了烟气温度为1 200 ℃、颗粒粒径为100 μm时，遮蔽因子与颗粒介质体积分数和声频率的关系.从图6可以看出，低频段遮蔽因子几乎为0，颗粒介质体积分数不变时，随着声频率的增大，遮蔽因子增大，即散射衰减系数α0增大；声频率不变时，颗粒介质体积分数越大，遮蔽因子越小，即散射衰减系数α0越小.同样还可以发现，随着多体多次散射次数的增加，遮蔽因子不断减小.

图6 不同颗粒介质体积分数下遮蔽因子随声频率的变化

图7给出了烟气温度为1 200 ℃、颗粒介质体积分数为0.2时，遮蔽因子与声频率和颗粒粒径的关系.从图7可以清晰地看出，声频率为20 Hz时，经过多体多次散射后，遮蔽因子趋近于0；声频率不变时，随着颗粒粒径的增大，遮蔽因子增大；颗粒粒径不变时，声频率越大，遮蔽因子越大.

图7 不同声频率下遮蔽因子随颗粒粒径的变化

图8(a)给出了声频率为5 kHz、颗粒介质体积分数为0.2时，遮蔽因子与烟气温度和颗粒粒径的关系.从图8(a)可以看出，颗粒粒径不变时，随着烟气温度的升高，遮蔽因子减小，散射衰减系数α0减小.图8(b)给出了声频率为5 kHz、颗粒粒径为100 μm时，遮蔽因子与烟气温度和颗粒介质体积分数的关系.从图8(b)可以看出，颗粒介质体积分数不变时，烟气温度越高，遮蔽因子越小，散射衰减系数α0越小.图8(c)给出了颗粒介质体积分数为0.2颗粒粒径为100 μm时，遮蔽因子与烟气温度和声频率的关系.从图8(c)可以看出，声频率不变时，烟气温度越高，遮蔽因子越小，散射衰减系数α0越小.

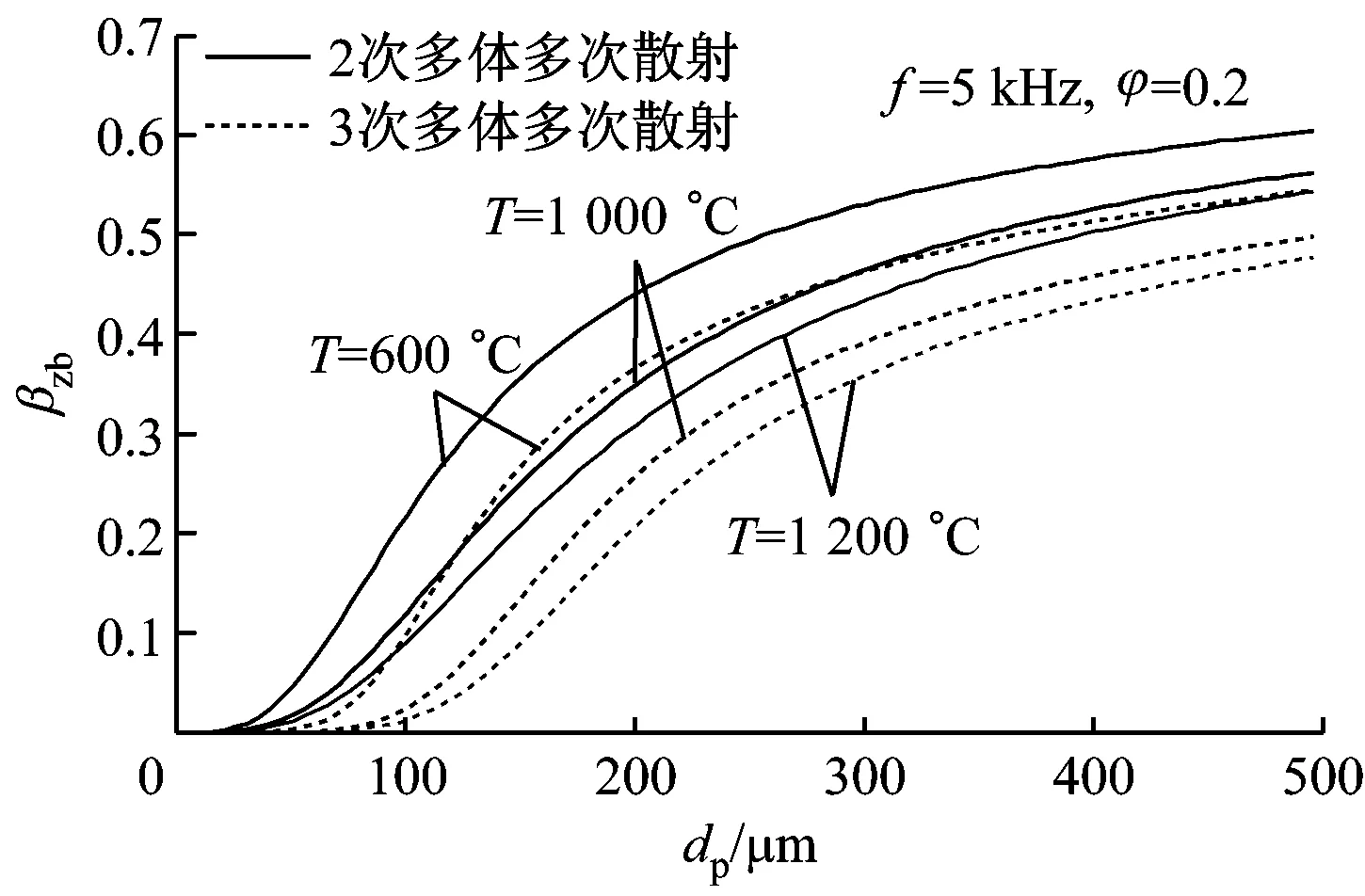
(a)

(b)

(c)

上文中得到了当n=2、3时遮蔽因子随烟气温度、颗粒粒径及颗粒介质体积分数的变化，而当n取无穷大时，可以得到在循环流化床锅炉炉膛参数下，可听声频率范围内有βzb≈0，即颗粒介质中由散射衰减和黏滞衰减引起的声衰减系数约为0，此时颗粒介质中的声波衰减主要由颗粒表面热传导耗散决定.这是因为散射波相互作用导致颗粒相互遮蔽，使被散射掉的部分声能重新回到入射方向，从而减小了声衰减系数.

2.2 散射波与黏滞波相互作用的颗粒介质中的声波衰减特性

(25)

(26)

(27)

当kR<<1时有：

(28)

(29)

(30)

根据数值计算，当n≥2时，βzb→0.因此，可以得到考虑散射波与黏滞波相互作用时，散射衰减和黏滞衰减引起的声衰减系数遮蔽因子约为0，即声衰减系数近似为0，此时炉膛中的声波衰减主要由颗粒表面的热传导耗散决定.考虑黏滞波的相互作用后声衰减系数进一步减小，主要原因是颗粒在黏滞流体中运动产生漩涡，将部分能量传给其周围的颗粒.

值得注意的是，在研究含颗粒介质气体中的声波衰减特性时对声波进行了平面波假设，实际传播过程中声波会出现球面发散，即发生球面传播衰减，但是当采取声阵列作为声源时，这部分衰减可以消除.

3 结 论

(1)在电站锅炉含颗粒介质的气体中，声波衰减主要来源于颗粒表面的热传导耗散以及黏滞衰减.

(2)颗粒介质体积分数较小时(燃煤锅炉中)，声衰减系数主要与烟气温度、颗粒介质体积分数、声频率及颗粒粒径有关.颗粒介质体积分数越大，声衰减系数越大；声频率越大，声衰减系数越大；颗粒粒径越大，声衰减系数越小；烟气温度越高，声衰减系数越大.当烟气温度不变时，所得声波衰减变化规律与实验结果吻合.

(3)颗粒介质体积分数较大时(如循环流化床中)，颗粒间的相互作用不能忽略.对于电站锅炉炉膛，由于散射波与黏滞波相互作用，散射衰减和黏滞衰减的声衰减系数几乎为0，声波衰减主要来源于颗粒表面的热传导耗散.

[1] 沈国清, 安连锁, 姜根山, 等. 基于声学CT重建炉膛二维温度场的仿真研究[J]. 中国电机工程学报, 2007, 27(2): 11-14.

SHEN Guoqing, AN Liansuo, JIANG Genshan, et al. Simulation of two-dimensional temperature field in furnace based on acoustic computer tomography[J]. Proceedings of the CSEE, 2007, 27(2): 11-14.

[2] 姜根山, 安连锁, 田静, 等. 炉管泄漏口喷流噪声的辐射特性[J]. 中国电机工程学报, 2010, 30(29): 24-29.

JIANG Genshan, AN Liansuo, TIAN Jing, et al. Acoustic radiation characteristics of jet noise from a boiler-tube leakage hole[J]. Proceedings of the CSEE, 2010, 30(29): 24-29.

[3] 姜根山, 安连锁, 杨昆. 锅炉换热器管道泄漏口声辐射指向性特征数值研究[J]. 中国电机工程学报, 2002, 22(6): 127-132.

JIANG Genshan, AN Liansuo, YANG Kun. Numerical study of directionality patterns for acoustic radiation from a leak source on a heat-exchanger cylinder in boilers[J]. Proceedings of the CSEE, 2002, 22(6): 127-132.

[4] 李言钦, 周怀春, 何其伟. 采用声波法监测四角切圆流场二维分布特性的模拟研究[J]. 中国电机工程学报, 2003, 23(11): 219-223.

LI Yanqin, ZHOU Huaichun, HE Qiwei. Simulation study on monitoring the two-dimensional characte ristics of the tangential flow field by using an acoustic method[J]. Proceedings of the CSEE, 2003, 23(11): 219-223.

[5] STOKES G G. On the effect of the internal friction of fluids on the motion of pendulums[J]. Transactions of the Cambridge Philosophical Society, 1851, 9: 8.

[6] SEWELL C J T. The extinction of sound in a viscous atmosphere by small obstacles of cylindrical and spherical form[J]. Phil Trans Toy Soc London, 1910, 210(566): 239-270.

[7] LAMB H. Hydrodynamics[M]. 6th ed. Cambridge, UK: Cambridge Univesity Press, 1945.

[8] QIAN Z W. Sound propagation in a medium containing bubbles and the splitting of the resonance peak[J]. Journal of Sound and Vibration, 1993, 168(2): 327-337.

[9] ALLEGRA J R, HAWLEY S A. Attenuation of sound in suspensions and emulsions: theory and experiments[J]. The Journal of the Acoustical Society of America, 1972, 51(5B): 1545-1564.

[10] SHENG Jinyu, HAY A E. An examination of the spherical scatterer approximation in aqueous suspensions of sand[J]. The Journal of the Acoustical Society of America, 1988, 83(2): 598-610.

[11] 钱祖文. 浓颗粒介质中的声传播和参数反演[J]. 自然科学进展, 1995, 5(1): 49-56.

QIAN Zuwen. Sound propagation and parameters inverse in concentrated suspension[J]. Progress in Natural Science, 1995, 5(1): 49-56.

[12] 杨文泽. 声波在气固两相流介质中传播特性的实验研究[D]. 保定: 华北电力大学, 2009.

[13] VALVERDE J M. Acoustic streaming in gas-fluidized beds of small particles[J]. Soft Matter, 2013, 9(37): 8792-8814.

[14] 钱祖文. 颗粒介质中的声传播及其应用[M]. 北京: 科学出版社, 2012.

Attenuation Characteristics of Acoustic Waves in Boiler Flue Gas Containing Solid Particles

JIANGGenshan1,XUWeilong2,ANLiansuo2

(1. Faculty of Mathematics and Physics, North China Electric Power University, Baoding 071003,Hebei Province, China; 2. School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China)

Numerical simulation was conducted on the attenuation mechanism of audio waves in the furnace of power plant boiler, based on which a formula of sound attenuation coefficient in the gas medium containing solid particles was built, so as to analyze the effects of following factors on the attenuation coefficient, such as the acoustic frequency, particle concentration, particle size and flue gas temperature, etc. Moreover, attenuation characteristics of acoustic waves in the furnace of fluidized bed boiler containing solid particles of higher volumetric fractions were also studied based on multi-body multiple scattering theory, and subsequently corresponding attenuation coefficients were corrected. Results show that for general coal-fired boilers, the sound attenuation coefficient increases with rising flue gas temperature, particle concentration and sound frequency, and with reducing particle size; whereas for fluidized bed boilers, the acoustic attenuation mainly originates from the thermal diffusion on the surface of medium particles.

power plant boiler; sound propagation; acoustic attenuation coefficient; multi-body multiple scattering theory

2016-02-01

2016-03-15

国家自然科学基金资助项目(11474091,11274111)；河北省自然科学基金资助项目(A2015502077)；中央高校基本科研业务费专项资金资助项目(2015XS105)

姜根山(1963-)，男，河北邢台人，教授，博士生导师，研究方向为锅炉声学理论及应用. 许伟龙(通信作者)，男，博士研究生，电话(Tel.):15632248235；E-mail：xuweilong@ncepu.edu.cn.

1674-7607(2017)02-0126-08

TV698.1+5

A 学科分类号：470.30