1 000 MW机组瞬态过程蓄热机理与煤耗计算

杨志平， 宋 阳， 郭喜燕， 孙伟鹏， 冯庭有

(1．华北电力大学 国家火力发电工程技术研究中心，北京 102206；2．华能海门电厂，广东汕头 515132)

1 000 MW机组瞬态过程蓄热机理与煤耗计算

杨志平1， 宋 阳1， 郭喜燕1， 孙伟鹏2， 冯庭有2

(1．华北电力大学 国家火力发电工程技术研究中心，北京 102206；2．华能海门电厂，广东汕头 515132)

建立了瞬态过程工质蓄热模型、金属蓄热模型和煤耗计算模型，对某1 000 MW机组瞬态工况试验过程进行了计算分析，得到了试验过程机组蓄热率和蓄热影响下机组发电标准煤耗增量曲线，分析了不同负荷下各受热面的蓄热分布情况，并与现场实测数据进行了对比.结果表明：机组总蓄热率与金属总蓄热率的变化趋势几乎一致，金属总蓄热率约为工质总蓄热率的1.5～2倍；工质蓄热率中水冷壁工质所占比例最大，过热器工质所占比例最小；受蓄热影响，机组升负荷试验过程中，发电标准煤耗最大增加了3.48 g/(kW·h)，而在降负荷试验过程中，发电标准煤耗最大减少了3.2 g/(kW·h).

1 000 MW机组； 蓄热模型； 瞬态工况试验； 煤耗

由于具有较低的设计煤耗和排放水平,超临界、超超临界燃煤发电机组已经成为优化我国火力发电结构的首选.截至2015年年底，我国已投产1 000 MW超超临界机组达85台.近年来,太阳能、风能等新能源快速增长，而新能源机组具有一次能源不能储存、功率输出随机等特点，使得新能源机组需要燃煤发电机组协同互补，因而燃煤发电机组面临更为频繁的调峰要求.我国火力发电年利用小时数逐年下降，2015年已降至4 329 h，大幅度瞬态工况逐渐成为燃煤发电机组运行的新常态.因此，深入分析大型燃煤发电机组在瞬态过程中的能耗，对于优化机组调峰运行方式、进一步挖掘机组节能潜力和提高机组运行经济性具有重要意义.

目前，对超超临界机组能耗的研究主要集中在稳态过程，仅有少数学者对其瞬态过程下的能耗进行了探讨.在机组大幅度调峰、启停等瞬态过程中，锅炉的汽水参数和金属壁面温度会发生较大改变，存在热量的存储和释放[1]，此时锅炉中工质吸收的热量并不等于燃料释放的热量，采用常规稳态模型计算机组煤耗必然会存在偏差.郭喜燕等[2-3]对瞬态过程锅炉内部热量分布情况进行了研究，定量分析了蓄热因素对机组煤耗的影响；成涛等[4]建立了超临界机组锅炉水冷壁瞬态过程蓄热模型；邓拓宇等[5]引入锅炉蓄热系数，对超超临界机组锅炉蓄热能力进行了定量计算；李爱娟[6]结合热力学第二定律对汽轮机侧瞬态工况下的能量分布进行了研究；Mishra等[7]对温度和流量扰动下换热器的瞬态特性进行了研究.上述对燃煤机组瞬态过程能耗的研究尚停留在模型建立阶段，缺乏现场实际数据验证.由于电厂各设备之间存在耦合作用从而相互影响，若直接取用电厂日常运行数据代入瞬态模型进行计算，会存在较多非瞬态因素干扰，对瞬态模型进行实际数据验证就需要电厂进行瞬态工况试验，隔离无关因素的干扰.然而，由于日常生产工作很难为机组安排试验，故国内外瞬态工况试验的案例较少.李学忠等[8-9]从试验数据层面分析了不同负荷升降率、负荷变动幅度和负荷波动次数对机组供电煤耗的影响，然而其研究未考虑蓄热因素的影响.

笔者基于热力学第一定律，在某1 000 MW超超临界燃煤机组瞬态工况试验数据的基础上采用集总参数法建立了金属壁面蓄热计算模型、按工质相态划分的工质蓄热计算模型以及瞬态过程机组煤耗计算模型，对试验过程中机组发电煤耗进行了计算和分析，并与正平衡发电煤耗进行了比较.

1 机组瞬态过程热力学模型

火电机组运行工况包括稳态工况和瞬态工况.系统负荷变化率较小的工况可近似视为稳态工况，而负荷变化率较大的工况(如机组启停、大幅度变负荷等)就必须考虑其间的过渡过程，其间各个工况为非稳态工况，也称为瞬态工况.对于稳态工况，忽略能量方程中的储能项，认为热侧流体释放的热量全部被工质吸收，不存在金属和工质的蓄热.对于瞬态工况，由于负荷和工质参数发生了较大变化，因此储能项不能忽略，需要考虑金属蓄热和控制体内工质蓄热的环节[10]，如图1所示.

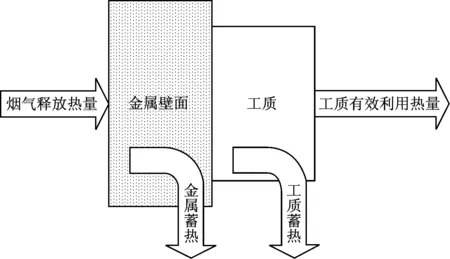
图1 瞬态过程能量的传递与转化

1.1 基本简化假设

为突出原理性分析，进行以下简化假设：

(1)在瞬态工况下，各个设备的金属和工质都存在蓄热现象，而锅炉的热惯性较大，故此处仅考虑锅炉蓄热.

(2)在实际瞬态过程中，水冷壁各段长度是动态变化的，但在某一负荷点附近，各段长度变化相对于各段的长度很小[11]，当负荷点确定时，水冷壁各段长度视为不变.

(3)受热面并排管束视为一根等效受热管，其面积为管束各受热面面积之和，等效受热管管壁厚度与各受热管管壁厚度相等.

(4)各受热面与外界环境没有热交换.

(5)水冷壁内工质的吸热量沿水冷壁长度方向均匀分布.

(6)水冷壁热水段选取工质进、出口比焓的算术平均值作为集总参数，水冷壁蒸发段选取蒸发段出口干度的一半作为集总参数[12]，其余受热面皆选取工质的出口压力和出口比焓作为集总参数.

1.2 工质蓄热模型

(1)

式中：U单相为单相工质控制体内能，kJ；τ为时间，s；ρ单相为单相工质控制体密度，m3/kg；h单相为单相工质控制体比焓，kJ/kg；t单相为单相工质控制体温度，℃；p单相为单相工质控制体压力，MPa；V单相为单相工质控制体体积，m3.

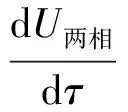
(2)

式中：U两相为两相工质控制体内能，kJ；p两相为两相工质控制体压力，MPa；V两相为两相工质控制体体积，m3；ρ′、ρ″分别为压力p两相下饱和水和饱和蒸汽的密度，m3/kg；h′、h″分别为压力p两相下饱和水和饱和蒸汽的焓值，kJ/kg；V′、V″分别为压力p两相下两相工质中液相和气相所占的体积，m3.

当水冷壁内工质处于亚临界状态时，将水冷壁划分为3段：热水段、蒸发段和蒸汽段.热水段和蒸汽段采用单相工质模型计算其蓄热率，而蒸发段则采用两相工质模型计算其蓄热率.当水冷壁内工质处于超临界状态时，就不存在两相蒸发区，此时水冷壁被划分为2段：热水段和蒸汽段，2段各自采用单相工质模型计算其蓄热率[13].

1.3 金属蓄热模型

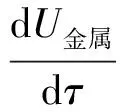
(3)

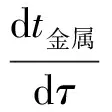
由式(3)可知，影响金属蓄热率的因素主要为金属质量、金属种类和金属壁面温度变化率.

1.4 瞬态过程煤耗计算模型

(4)

第i个受热面蓄热率为ΔQi，则n个受热面的蓄热率相加即为机组总蓄热率ΔQ总：

(5)

在传统的稳态过程发电煤耗计算模型基础上，笔者以机组蓄热影响发电煤耗增量ΔB作为修正项，得到了瞬态过程发电煤耗计算模型如下：

(6)

式中：B为瞬态过程发电煤耗；Bsteady为稳态过程发电煤耗；ΔB为机组蓄热影响发电煤耗增量.

(7)

(8)

式中：Qsteady为稳态工况下汽轮机热耗率，kJ/s；ηb为锅炉效率；Qd为燃煤低位发热量，kJ/kg.

进一步可得机组蓄热影响发电标准煤耗增量Δb为

(9)

式中：P为机组负荷.

2 超超临界燃煤机组瞬态工况试验

为进一步研究瞬态过程对超超临界燃煤机组发电煤耗的影响，对某1 000 MW超超临界燃煤机组进行了瞬态工况试验.该机组锅炉为东方锅炉股份有限公司生产的复合变压运行超超临界本生直流锅炉，型号DG3000/26.15-Ⅱ，锅炉采用一次再热、前后墙对冲燃烧、单炉膛、尾部双烟道结构，其受热面主要结构参数见表1.

表1 锅炉主要结构参数

机组进行瞬态工况试验期间负荷变动均采用手动控制，维持除氧器和凝汽器水位的稳定，对机组外漏点和补水进行彻底隔离，另外机组汽、水运行采用单元制.试验过程中还需注意滑压运行或定压运行时相应地维持主蒸汽温度、主蒸汽压力、再热蒸汽温度、再热蒸汽压力和排汽压力等参数稳定，并对其值进行修正.机组燃用煤种固定，煤种工业分析结果见表2，试验开始后每隔3 min对炉渣、飞灰取样化验一次，每隔0.5 min取一次机组热力数据.

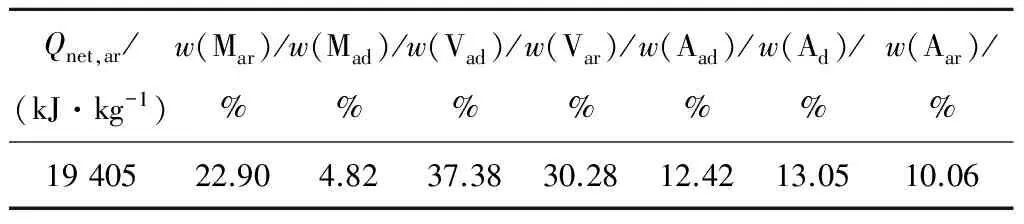
表2 试验煤种工业分析

试验时间共450 min，试验的整个负荷变化过程为400 MW→1 000 MW→450 MW，在0～25 min时间段机组负荷先稳定在400 MW；在25～125 min时间段机组负荷从400 MW升至1 000 MW；在125～400 min时间段机组负荷稳定在1 000 MW；在400～450 min时间段机组负荷再降至450 MW.试验过程机组负荷随时间的变化曲线如图2所示.

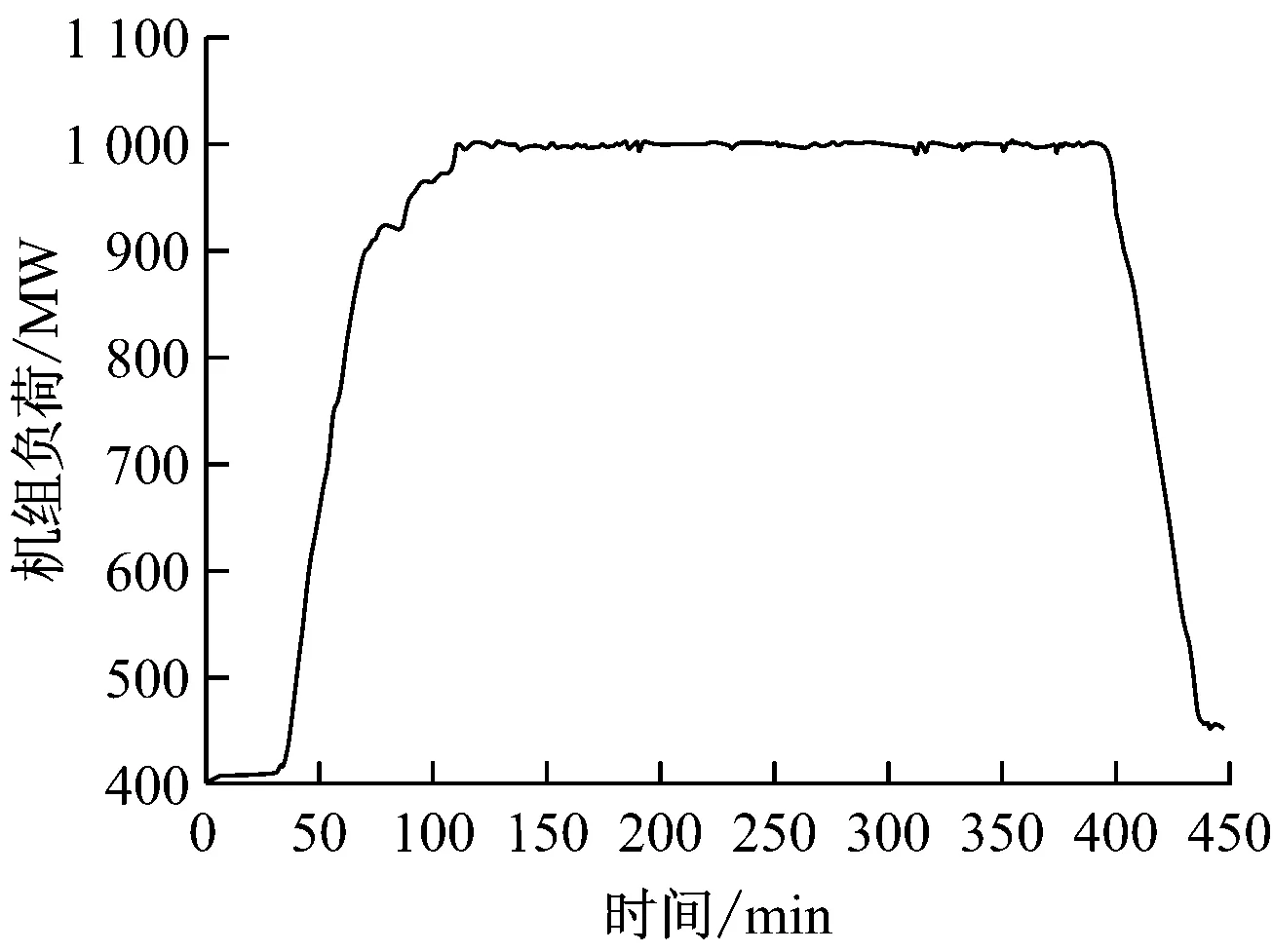
图2 试验过程机组负荷随时间的变化

瞬态工况试验过程机组负荷变化率随时间的变化曲线如图3所示，机组负荷变化率为“+”代表机组负荷升高，机组负荷变化率为“-”代表机组负荷降低.在试验过程中，机组负荷变化率应尽量维持在1～1.5 %/min锅炉最大连续蒸发量(BMCR)，最大不超过3 %/min BMCR.在升负荷阶段初期，机组负荷变化率随着机组负荷的升高而升高，极值达到17 MW/min，而后随着升负荷阶段的结束，机组负荷变化率也开始下降，直到机组负荷稳定在1 000 MW时机组负荷变化率重新变为0；在降负荷阶段机组负荷变化率负向变化，也是先增后降，与升负荷阶段相似，极值达-18 MW/min.

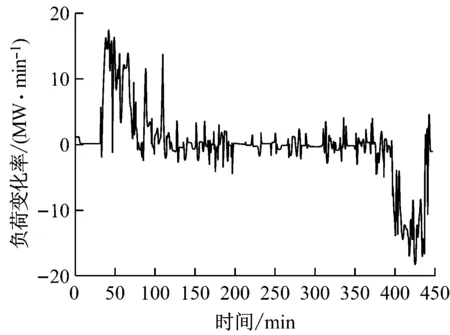
图3 试验过程机组负荷变化率曲线

瞬态工况试验过程中，锅炉效率曲线如图4所示.在升负荷阶段，锅炉效率随着机组负荷的升高而升高，在82.5 min时，机组负荷达到921 MW，此时锅炉效率达到最大值94.6%，而后机组负荷继续升高，锅炉效率反而下降，当机组负荷维持在1 000 MW稳态时，锅炉效率稳定在94.2%附近；但在降负荷阶段，锅炉效率的变化与升负荷阶段有较大不同，在机组负荷降至920 MW左右时锅炉效率并未出现明显提升，而是继续下降.

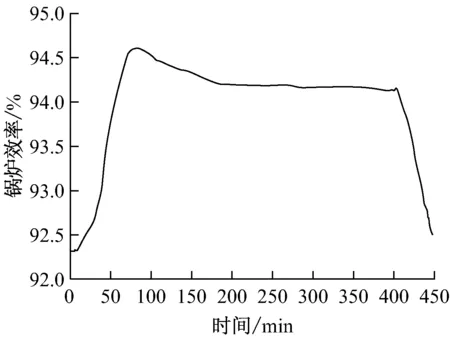
图4 试验过程锅炉效率曲线

3 案例计算结果

3.1 机组瞬态过程蓄热及分布结果

利用上述模型对瞬态工况试验过程中机组的蓄热特性进行计算，机组工质蓄热率、金属蓄热率和总蓄热率分别如图5、图6和图7所示，蓄热率为“+”代表吸热，为“-”代表放热.

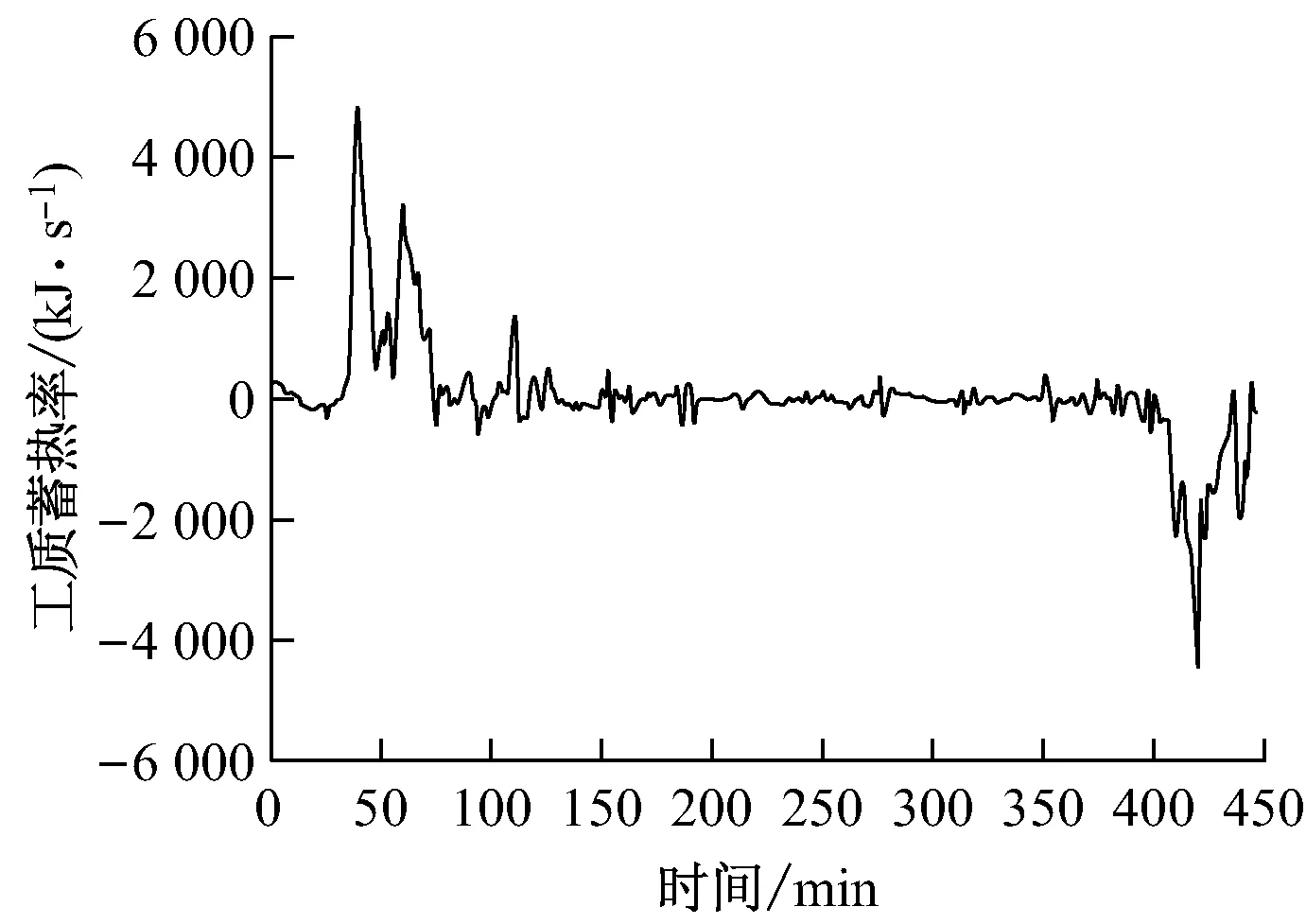
图5 工质蓄热率

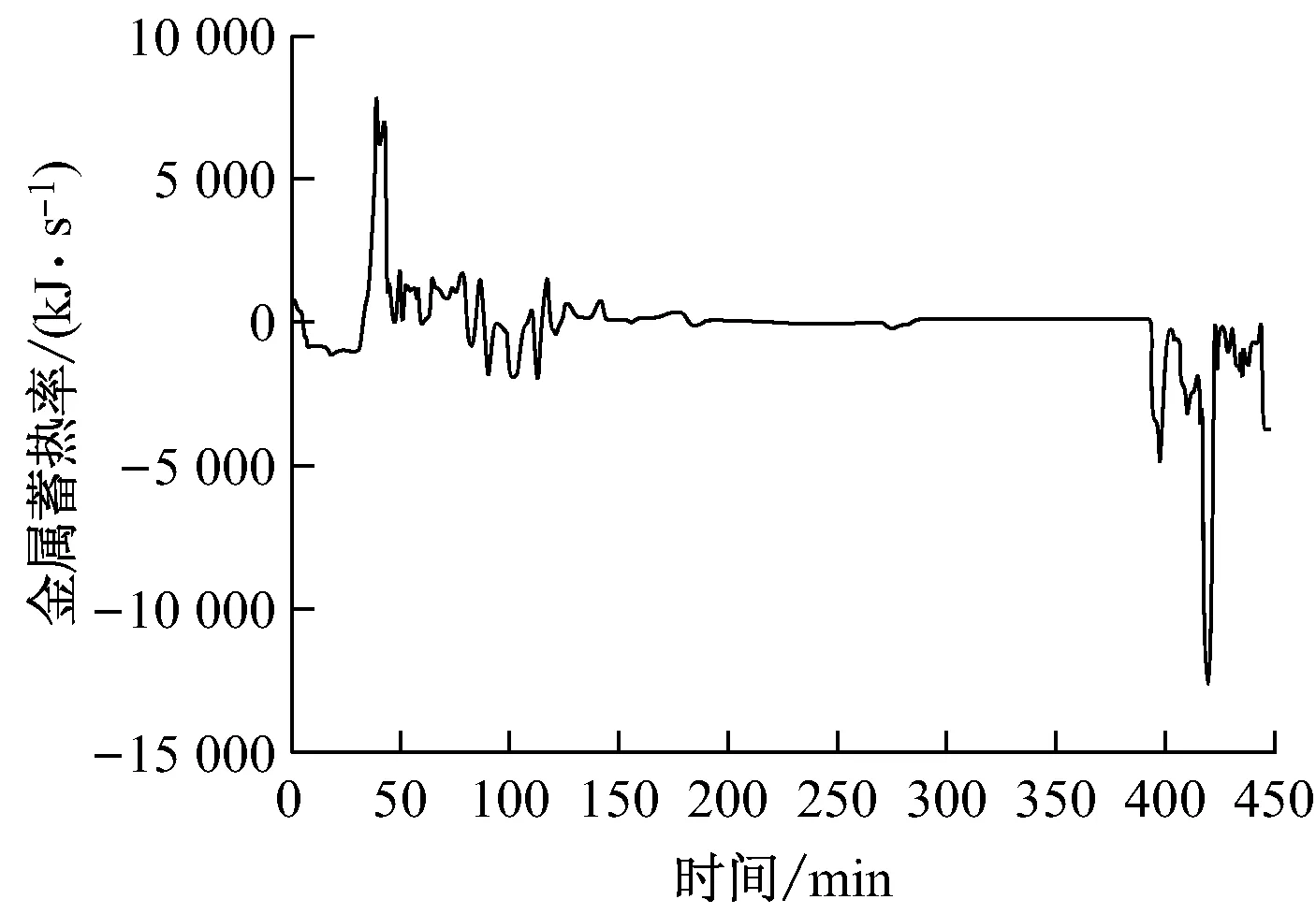
图6 金属蓄热率

比较图5和图6可知，同一时刻金属蓄热率比工质蓄热率大，为工质蓄热率的1.5～2倍，虽然各受热面金属壁面的温度变化率和工质的温度变化率相差不大，处于同一数量级，但金属壁面的质量却十分巨大，由表1可见各设备的金属质量处于千吨数量级，所以金属蓄热率远大于工质蓄热率，故总蓄热率更容易受金属蓄热率的影响，总蓄热率和金属蓄热率的图形几乎一致.另外需要注意的是，在75～150 min时间段内工质蓄热率和金属蓄热率均出现了较大波动，结合图2和图3分析其原因为:在升负荷阶段的末期机组负荷变化率不稳定，该情况属于不可控误差.

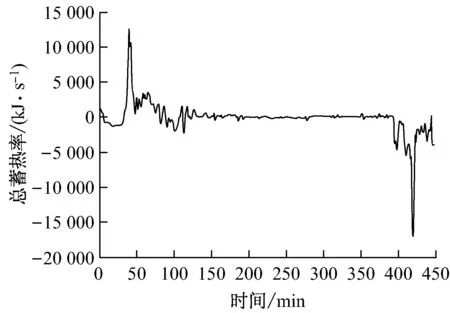
图7 总蓄热率

为了更好地比较不同设备受热面的工质蓄热率和金属蓄热率情况，分别选取升负荷阶段40%额定负荷(THA)、60%THA、80%THA和100%THA 4个工况,计算各受热面蓄热率所占比例，结果如表3和表4所示.

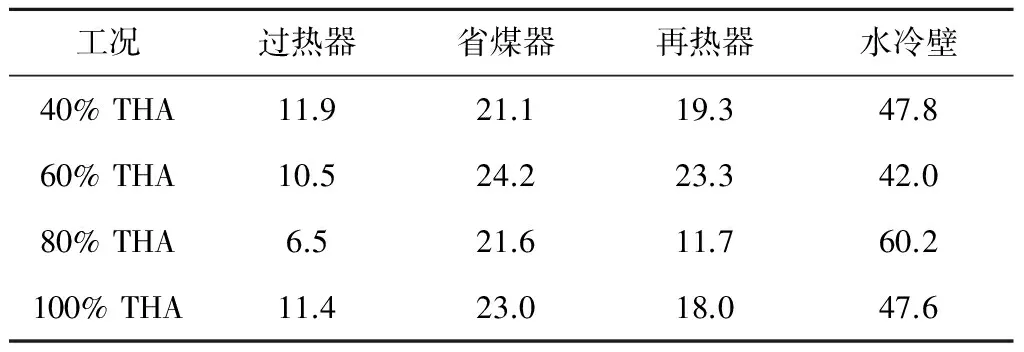
表3 不同机组负荷下各受热面工质蓄热率所占比例

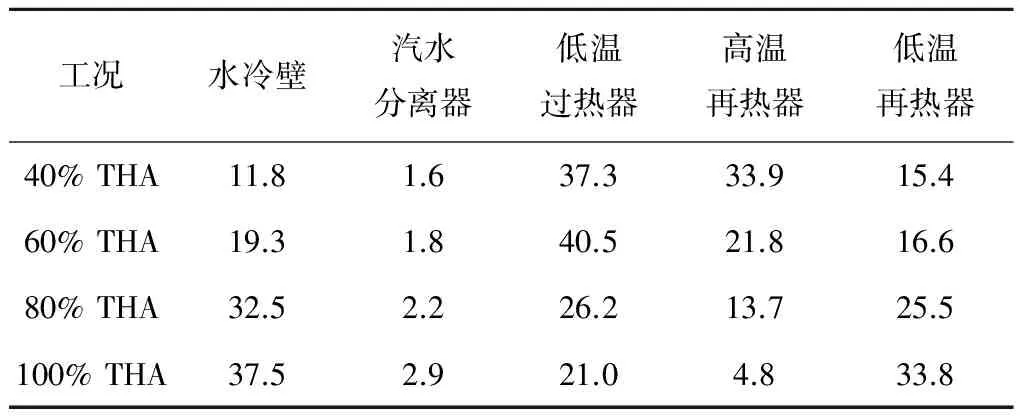
表4 不同机组负荷下各受热面金属蓄热率所占比例

由表3可见，在40%THA、60%THA、80%THA和100%THA 4个工况下，工质蓄热率最大的受热面均为水冷壁，分别占总工质蓄热率的47.8%、42.0%、60.2%和47.6%；其次是省煤器，再次是再热器，最后是过热器.

水冷壁内工质蓄热率所占比例最大，这是因为在水冷壁内工质经历了由热水变为高温高压蒸汽的相变过程，工质参数变化十分显著，尤其是当机组负荷从60%THA升至80%THA时，工质完成了从亚临界状态向超临界状态的转变，工质参数变化最为剧烈，并且工质蓄热特性参数有了较大的提升，此时水冷壁工质蓄热率比例提升了18.2%，而后随着机组负荷的逐渐稳定，工质蓄热率所占比例降至47.6%.对于过热器与再热器，由于在瞬态工况试验过程中需要根据运行方式对过热蒸汽的温度和压力、再热蒸汽的温度和压力进行维持，导致这2个受热面内工质的参数变化有限，故其工质蓄热率所占比例较低.

由于运行过程中电厂对过热蒸汽温度调控的要求较高，导致过热器出口蒸汽温度变化较小，故忽略过热器高温段金属蓄热.而省煤器的金属质量较小，导致其金属蓄热率较小，故也忽略省煤器金属蓄热.由表4可见，在40%THA和60%THA工况下，低温过热器金属蓄热率所占比例最大，分别为37.3%和40.5%；而在80%THA和100%THA工况下，水冷壁金属蓄热率所占比例最大，分别为32.5%和37.5%.就各受热面蓄热率所占比例的变化来看，水冷壁、汽水分离器和低温再热器的金属蓄热率所占比例均随着负荷上升而升高，水冷壁金属蓄热率比例从11.8%提升至37.5%，汽水分离器金属蓄热率比例从1.6%提升至2.9%，低温再热器金属蓄热率比例从15.4%提升至33.8%.而高温再热器金属蓄热率所占比例则随着负荷的上升而降低，从33.9%降至4.8%.

在低负荷时，机组采用的是定压运行，此时再热器出口蒸汽温度的变化率较大，故此时高温再热器的金属蓄热率也较大.而随着机组负荷上升，机组转而采用滑压运行，再热器出口温度趋于稳定，温度变化率减小，故高温再热器的金属蓄热率也随之变小.而水冷壁由于受炉膛辐射换热影响较大，其金属温度随机组负荷的变化更为敏感，故虽然水冷壁的金属质量并非最大但其蓄热率所占比例却是最大的.

图7为机组瞬态工况试验过程中总蓄热率的变化曲线.从25 min开始机组进入升负荷阶段，各受热面的工质和金属壁面开始吸热，在39.5 min机组负荷达到496.795 MW时，工质蓄热率和金属蓄热率达到正极大值，分别为4 926 kJ/s和8 169 kJ/s，总蓄热率为13 095 kJ/s，此后随着机组升负荷阶段结束进入稳定状态，机组负荷变化率开始下降,从而工质蓄热率和金属蓄热率也随之下降，直到机组负荷稳定蓄热结束.从400 min起机组开始进入降负荷阶段，各受热面的工质和金属开始放热，则蓄热率开始负增加，在420 min负荷达到698.909 MW时工质蓄热率和金属蓄热率达到负极大值，分别为-4 427 kJ/s和-12 638 kJ/s，总蓄热率为-17 065 kJ/s，此后随着机组降负荷阶段结束,负工质蓄热率和金属蓄热率也重新变为零.

3.2 机组瞬态过程煤耗计算结果

依据式(9)可计算工质蓄热率、金属蓄热率和总蓄热率影响下发电标准煤耗的增量，结果如图8～图10所示，“+”代表发电标准煤耗增加，“-”代表发电标准煤耗减少.

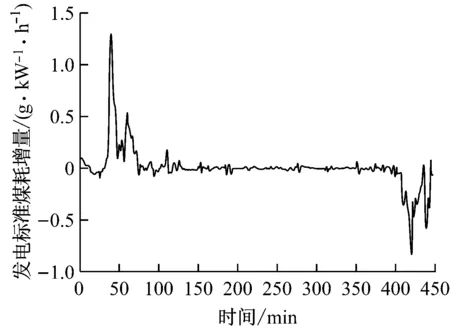
图8 工质蓄热率影响下的发电标准煤耗增量

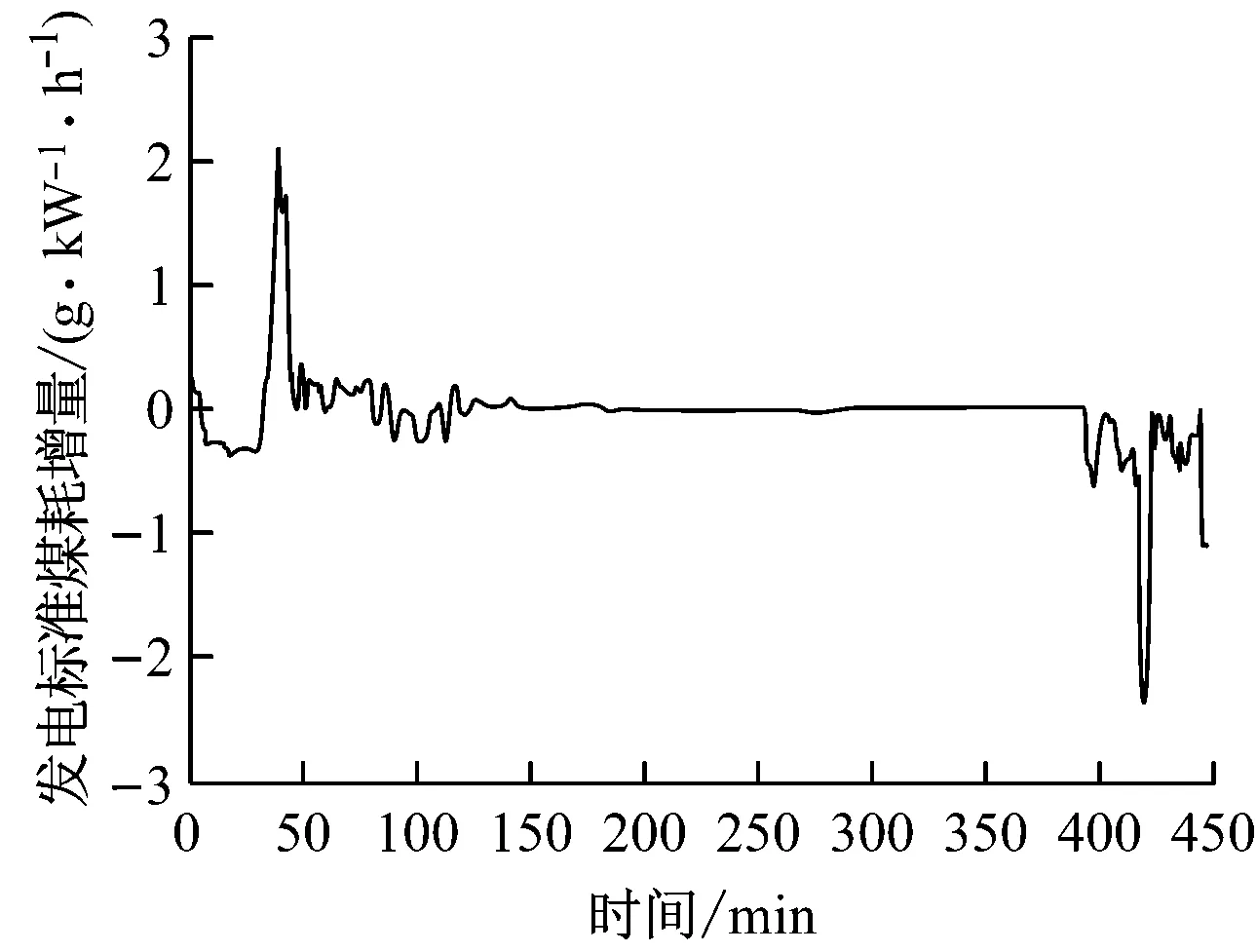
图9 金属蓄热率影响下的发电标准煤耗增量

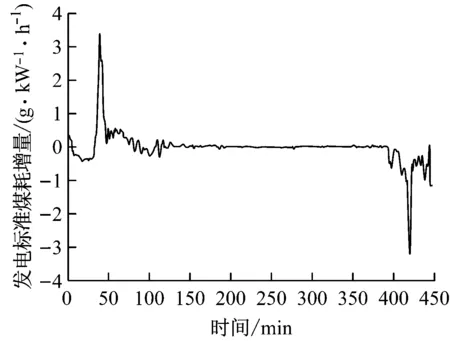
图10 总蓄热率影响下的发电标准煤耗增量

对比图8～图10可知，发电标准煤耗增量与蓄热率的变化趋势基本保持一致.在瞬态工况试验过程中锅炉效率虽然也有变化，但其变化范围仅为±2%，对发电标准煤耗增量的影响十分有限.发电标准煤耗增量的极值也出现在496.795 MW和698.909 MW，当机组负荷升至496.795 MW时，工质蓄热率影响下的发电标准煤耗增加1.31 g/(kW·h)，金属蓄热率影响下的发电标准煤耗增加2.17 g/(kW·h)；当机组负荷降至698.909 MW时，工质蓄热率影响下的发电标准煤耗减少0.83 g/(kW·h)，金属蓄热率影响下的发电标准煤耗减少2.37 g/(kW·h).

3.3 结果对比验证

综合考虑瞬态过程中蓄热率因素的影响，计算得到瞬态过程机组发电标准煤耗，并与机组正平衡发电标准煤耗进行比较，用以验证瞬态过程煤耗计算模型的精度.入炉煤量是计算正平衡发电标准煤耗的重要参数，目前常用的电厂入炉煤量确定方法包括利用给煤机自身附带的计量装置直接测量，或利用电子皮带秤计量并确定机组燃煤量，同时需要综合考虑计量设备校验和老化情况选择计量方法.试验电厂已对给煤机计量装置进行校验，称重精度在±0.5%以内.

特定负荷及工况(如x%THA)下，机组正平衡发电标准煤耗可由式(10)计算得到：

(10)

式中：b正平衡为机组正平衡发电标准煤耗，g/(kW·h)；Q1为达到(x-3)% THA负荷时记录的给煤机累计给煤量，t；Q2为达到(x+3)% THA负荷时记录的给煤机累计给煤量，t；P′为x% THA工况机组的发电功率，MW；Δτ为负荷变化时间，以升负荷过程为例，即机组负荷从(x-3)% THA升至(x+3)% THA的时间，min.

需要说明的是，考虑到给煤量计量值与机组负荷间存在延迟，选取二者之间的延迟时间为3 min.升负荷阶段选取40%THA、50%THA、75%THA和100%THA 4个工况进行煤耗对比，而由于降负荷时只降至450 MW，故只选取50%THA、75%THA和100%THA 3个工况进行煤耗对比，结果如表5和表6所示.

表5和表6所示为瞬态工况试验升负荷和降负荷时，蓄热率因素对发电标准煤耗增量的定量影响.考虑到变负荷过程中机组负荷变化率先增大后减小，蓄热率因素对发电标准煤耗增量的影响呈现先增大后减小的变化趋势.在瞬态工况下用常规方法求得稳态煤耗与现场测量煤耗差距较大，平均误差达0.4%以上.而考虑蓄热率因素影响后,求得瞬态过程发电标准煤耗与现场测量煤耗的正负误差均在0.3%以内，模型精度足以满足电厂实际运行要求.

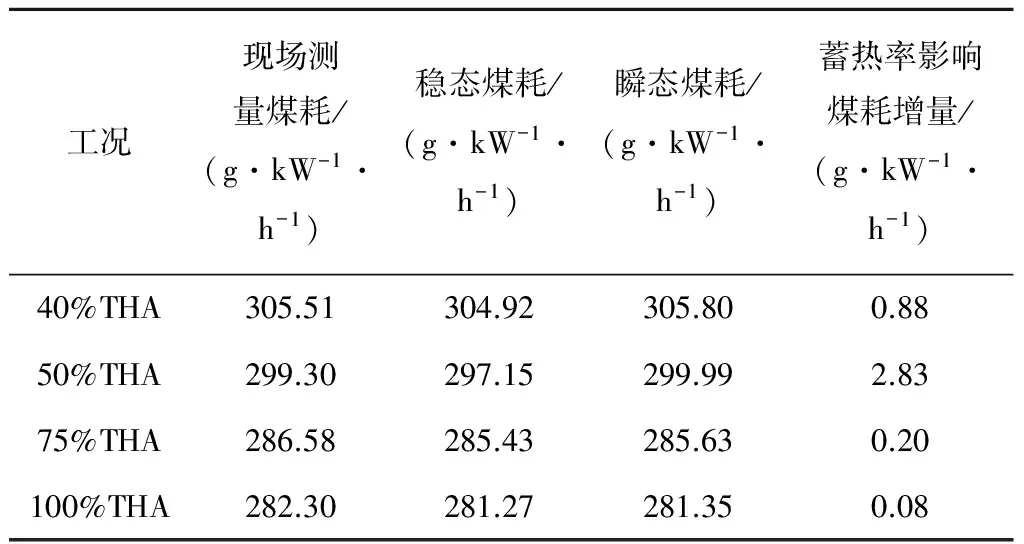
表5 升负荷阶段发电标准煤耗计算结果对比

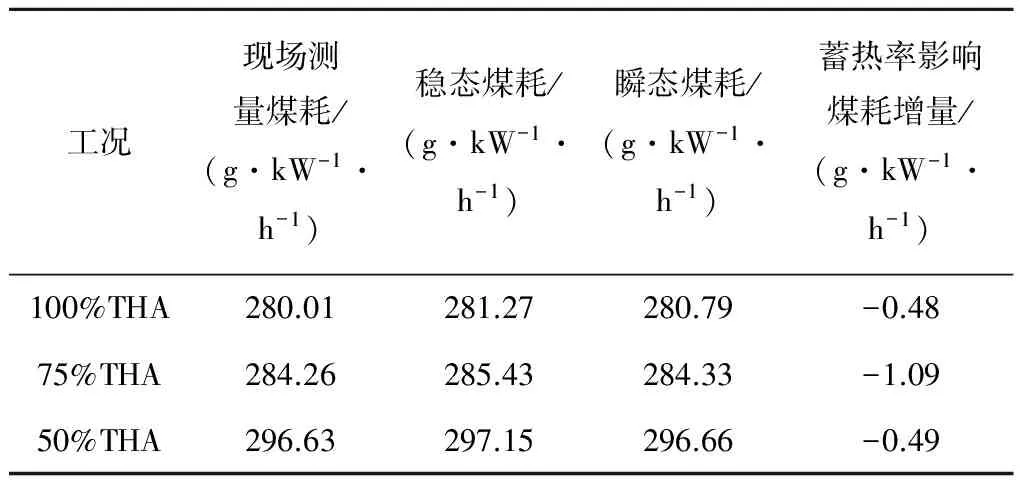
表6 降负荷阶段发电标准煤耗计算结果对比

4 结 论

(1)考虑到锅炉各受热面金属质量巨大，瞬态过程中总蓄热率变化趋势与金属蓄热率变化趋势基本一致，而金属蓄热率约为工质蓄热率的1.5～2倍.

(2)水冷壁内工质发生相变的过程中工质参数变化十分剧烈，所以水冷壁的工质蓄热率所占比例最大.由于机组运行过程中需要尽量维持过热蒸汽和再热蒸汽参数稳定，导致过热器和再热器内工质的参数变化有限，故其工质蓄热率所占比例最小.

(3)高温再热器金属蓄热率所占的比例随着机组负荷的上升而降低，这是机组由定压运行转为滑压运行，再热器出口蒸汽温度趋于稳定所致.而水冷壁、汽水分离器和低温再热器金属蓄热所占比例均随着机组负荷上升而升高，其中水冷壁金属蓄热所占比例最大，这是因为水冷壁受炉膛辐射换热影响较大，其金属温度随负荷的变化更为敏感.

(4)受蓄热率影响，机组升负荷试验过程中，发电标准煤耗最大增加了3.48 g/(kW·h)，而在降负荷试验过程中，发电标准煤耗最大减少了3.2 g/(kW·h)，模型计算瞬态过程发电标准煤耗与现场测量煤耗的正负误差不超过0.3%，模型精度满足电厂实际运行要求.

[1] 刘吉臻, 秦志明, 张栾英, 等. 汽包锅炉蓄热分析与计算[J]. 动力工程学报, 2012, 32(2): 96-100.

LIU Jizhen, QIN Zhiming, ZHANG Luanying, et al. Analysis and calculation of heat storage capacity in drum boilers[J]. Journal of Chinese Society of Power Engineering, 2012, 32(2): 96-100.

[2] 郭喜燕, 杨勇平, 王修彦, 等. 机组非稳态工况下锅炉中的热量分布[J]. 动力工程, 2007, 27(5): 667-671.

GUO Xiyan, YANG Yongping, WANG Xiuyan, et al. Heat distribution in utility boilers operating under unsteady operating conditions[J]. Journal of Power Engineering, 2007, 27(5): 667-671.

[3] 郭喜燕, 杨勇平, 王修彦, 等. 锅炉蓄热过程对机组煤耗的影响分析[J]. 中国电机工程学报, 2007, 27(26): 30-34.

GUO Xiyan, YANG Yongping, WANG Xiuyan, et al. Analysis on effect of heat storage in boiler upon coal consumption of power generating unit[J]. Proceedings of the CSEE, 2007, 27(26): 30-34.

[4] 成涛, 郭喜燕, 李季. 超临界直流锅炉水冷壁广义全工况能量分析[J]. 锅炉技术, 2015, 46(1): 1-7, 26.

CHENG Tao, GUO Xiyan, LI Ji. Energy analysis on generalized full work conditions of water cooled wall of supercritical once-through boiler[J]. Boiler Technology, 2015, 46(1): 1-7, 26.

[5] 邓拓宇, 田亮, 刘吉臻. 超超临界直流锅炉蓄热能力的定量分析[J]. 动力工程学报, 2012, 32(1): 10-14, 20.

DENG Tuoyu, TIAN Liang, LIU Jizhen. Quantitative analysis on heat storage capacity of ultra-supercritical once-through boilers[J]. Journal of Chinese Society of Power Engineering, 2012, 32(1): 10-14, 20.

[6] 李爱娟. 机组汽轮机系统瞬态工况能量分布的研究[D]. 北京: 华北电力大学, 2012.

[7] MISHRA M, DAS P K, SARANGI S. Transient behaviour of crossflow heat exchangers due to perturbations in temperature and flow[J]. International Journal of Heat and Mass Transfer, 2006, 49(5/6): 1083-1089.

[8] 李学忠, 孙伟鹏, 冯庭有, 等. 百万千瓦机组瞬变负荷能耗特性试验研究[J]. 现代电力, 2011, 28(2): 58-64.

LI Xuezhong, SUN Weipeng, FENG Tingyou, et al. Experimental research on the energy consumption of the instantaneous load in 1 036 MW unit[J]. Modern Electric Power, 2011, 28(2): 58-64.

[9] 孙伟鹏, 孙叶柱. 超超临界机组瞬变负荷对供电煤耗率的影响[J]. 中国电力, 2012, 45(1): 20-24.

SUN Weipeng, SUN Yezhu. The influence of instantaneously variable load on coal consumption rate in ultra supercritical unit[J]. Electric Power, 2012, 45(1): 20-24.

[10] 成涛. 大幅度变工况机组能耗分析[D]. 北京: 华北电力大学, 2014.

[11] 谷俊杰, 张永涛, 曹喜果, 等. 超(超)临界直流锅炉蓄热系数计算[J]. 动力工程学报, 2015, 35(3): 173-177.

GU Junjie, ZHANG Yongtao, CAO Xiguo, et al. Calculation of heat storage coefficient for ultra supercritical once-through boilers[J]. Journal of Chinese Society of Power Engineering, 2015, 35(3): 173-177.

[12] 梁庆姣. 超超临界机组核心模型的建立与仿真分析[D]. 北京: 华北电力大学, 2012.

[13] 秦志明, 刘吉臻, 张栾英, 等. 超临界直流锅炉蓄热的分析与计算[J]. 动力工程学报, 2013, 33(4): 250-255.

QIN Zhiming, LIU Jizhen, ZHANG Luanying, et al. Analysis and calculation of heat storage in supercritical once-through boilers[J]. Journal of Chinese Society of Power Engineering, 2013, 33(4): 250-255.

Heat Storage Mechanism and Coal Consumption Calculation of a 1 000 MW Power Unit Under Transient Conditions

YANGZhiping1,SONGYang1,GUOXiyan1,SUNWeipeng2,FENGTingyou2

(1. National Thermal Power Engineering & Technology Research Center, North China Electric Power University, Beijing 102206, China; 2. Huaneng Haimen Power Plant, Shantou 515132, Guangdong Province, China)

Models to calculate the coal consumption and heat storage rate of the working medium and metallic materials of a 1 000 MW power unit under trainent conditions were established, based on which, calculation and analysis were performed on the transient test process of the unit, so as to obtain the curves of standard coal consumption rate for power generation corresponding to the heat storage rate and under the heat storage effect during the test, analyze the distributions of heat storage on various heating surfaces at different loads, and to compare the test results with field data. Results show that the total heat storage rate of the unit varies in the same trend with that of metallic materials, and the latter is 1.5-2.0 times of the working medium. Water walls share the largest proportion in the heat storage of working medium, while superheaters share the least. Affected by heat storage, the standard coal consumption rate is at most increased by 3.48 g/(kW·h) during loading up period and decreased by 3.2 g/(kW·h) during loading down period.

1 000 MW unit; heat storage model; transient test; coal consumption

2016-04-05

2016-05-15

国家重点基础研究发展计划资助项目(973计划)(2015CB251505)；国家自然科学基金资助项目(U1261210，51306050)；中央高校基本科研业务费专项资金资助项目(2015MS43，2015XS81，2014XS19，2014XS13)

杨志平(1968-)，男，山西天镇人，高级工程师，博士，研究方向为火电机组热力系统节能理论与技术. 电话(Tel．)：13671002249；E-mail：yzprr@163.com.

1674-7607(2017)02-0140-08

TK122

A 学科分类号：470.20