基于免疫策略的债券投资组合实证研究
信怀义


摘 要:基于我国债券市场2003年1月-2016年6月的国债数据,采用利率免疫策略对债券投资组合管理、应用视图进行实证分析,研究表明有较多非平行因素影响我国银行间债券市场国债收益率曲线的变动。从实证结果看,在利用免疫策略构建债券投资组合规避利率风险时,单一久期匹配策略可能难以发挥较好的效果,多维久期匹配策略能够较好地规避利率波动对目标收益率的影响,免疫效果相对最差的是单一久期匹配策略,免疫效果相对最佳的是三维久期匹配策略,其他策略的免疫效果介于二者之间。
关键词:债券投资组合;久期匹配策略;免疫策略;单一久期策略
中图分类号:F832.5 文献标识码:A 文章编号:1003-3890(2017)01-0051-07
一、引言
中国经济正处在转型深化期,建立多层次债券市场体系是降低实体企业融资成本、促进金融市场内生动力、提升市场经济运行效率、深化经济体制全面改革的基本途径。因此,需要充分发挥金融资源在经济活动中的配置作用。
国务院于1981年1月颁布了《中华人民共和国国库券条例》,标志着重启国债发行,我国债券市场由此进入新阶段。经过30多年的探索和发展,我国债券市场发生了深刻变革,市场结构形成了由交易所市场、商业银行柜台市场、銀行间市场等构成的多层次市场体系;产品结构形成了由国债、金融债券、公司债券等构成的多元化品种;市场规模已经达到52.33万亿元(截至2016年3月底各类债券合计余额),在经济发展中发挥了巨大作用。
在这种情况下,债券投资者如何选择策略构建债券投资组合提高收益率,如何识别、度量和控制债券投资组合风险,从而提高债券投资管理水平、实现稳健经营,具有重要的现实意义。
本文在对主要的债券投资组合模型与方法进行简述后,基于银行间债券市场讨论和研究投资组合配置与风险防控之间的相关问题,并在债券投资组合管理策略中引入免疫策略,对其应用表现进行实证检验。
二、债券投资组合研究综述
从1952年Markowtiz提出现代投资组合理论(Modern Portfolio Theory,简称MPT),到1964年Sharpe et al.提出的资本资产定价模型(Capital Asset Pricing Model,简称CAPM)、1965年Fama提出的有效市场假说(Efficient Markets Hypothesi,简称EMH)、1976年Ross提出的套利定价理论(Arbitrage Princing Theory,简称APT)、1979年Kahneman提出的行为金融学(Behavioral Finance,简称BF)、2010年吴德俊提出的演化证券学(Evolutionary Analysis Theory of Security,简称EAS)。这些研究成果大大加快了现代投资组合理论演进的历程。
(一)国外研究综述
Markowitz(1952)[1]在其经典之作《资产选择》中首次用数学领域的均值和方差这两个概念来量化分析应用资产组合报酬,系统地阐述了资产组合及其选择问题,开启了金融数理分析的先河。Bieewag et al.(1983)[2]通过对债券投资组合的深入研究,首次构建了多期免疫策略,并对其基本原则进行了系统性的总结。Fisher et al.(1971)[3]、Fong et al.(1984)[4]将组合投资的免疫策略进行了重大改进,通过构建的凸性方法来测度利率风险,从此基于久期凸性套期保值法被理论界和实务界广泛应用和发展。但是Barrett et al.(1995)[5]以及Ho(1992)[6]对久期凸性套期保值法进一步研究发现此方法并不能适用于收益率曲线的非平行移动。从这些实证研究得出,美国国债利率期限结构风险隐含着三个典型的特征,分别是:短期利率的波动率大于长期利率的波动率,意味着风险也大;Sundaresan(2002)[7]研究得出,无论利率水平曲线还是利率波动率曲线都和收益率曲线具有相关性;Diebold et al.(2006)[8]研究得出,利率水平分布具有厚尾特性。
Litterman et al.(1991)[9]采用主成分分析方法对美国利率期限结构进行研究时发现有三个主要因素影响着96%的期限结构变动,分别是水平因素、斜率因素和曲率因素。Marida et al.(2005)[10]采用多因子模型对公司债券组合进行研究时形成了一套信用风险免疫组合管理方法。Soto(2004)[11]也采用主成分分析方法对西班牙国债收益率曲线进行了分析,发现同样有三个因素合计对收益率曲线波动的影响高达90%以上,这三个因素不完全相同,第一、第二个分别是长期利率、长短期利差,第三个因素也是曲率因素。
(二)国内研究综述
我国债券市场自1981年重新起步发展到2003年逐步成型,目前已初具规模。由此可见,国内学者和业界人士无论在债券市场的理论研究还是在实证研究方面都相对较晚,相关的研究还较为缺乏。目前主要集中于以下三个方面:
1. 基于利率期限结构视角的探究。陈雯 等(2002)[12]、郭涛 等(2007)[13]、宋逢明 等(2006)[14]、杨大楷 等(1997)[15]、姚长辉 等(1998)[16]、朱世武 等(2003)[17]、周荣喜 等(2004,2005)[18-19]、周子康 等(2008)[20]分别基于不同的利率期限结构视角对债券投资组合进行了实证探究。
2. 基于债券投资组合配置视角的探究。王实 等(1996)[21]研究债券投资组合时,构建了随机规划模型,并对其应用问题进行深入研究。黄兴 等(2000)[22]对银行债券投资组合的优化问题进行了研究,构建了资产负债久期匹配模型。朱世武 等(2004)[23]基于动态套期保值策略的崭新视角,采用上海交易所的数据,进一步实证研究了债券投资组合优化问题。刘琳琳(2006)[24]采用模型对债券投资组合的免疫策略进行了进一步研究,发现其免疫效果更佳。
3. 基于债券投资组合风险度量视角的探究。唐革榕 等(2003)[25]利用主成分分析方法,对上交所国债收益率曲线进行研究,与Litterman et al.(1991)[9]发现的三个主要因素相同,但只是影响收益率曲线的90%左右的变动。刘川巍(2004)[26]以内部管理角度,分析了银行债券资产的利率风险特性、成因和影响因素,并对如何控制这些风险给出了对策建议。王志强 等(2009)[27]采用上海证券交易所上市国债的交易数据,对比分析了Macaulay久期、修正久期、Fisher-Weil久期、方向久期、Nelson-Siegel部分久期和近似久期等6种久期配比策略,深入研究了它们的免疫效果及其稳定性,发现6个策略中最好的是Nelson-Siegel部分久期配比策略,最差的是方向久期配比策略,其他4种没有明显差异。
三、债券投资组合利率免疫策略
利率风险是债券投资组合面临的主要风险之一,其形成主要有两种可能性,其一是债券持有者在进行债券交易时的资本损失,其二是利息再投资时投资收益率低于债券购买时的收益率。
Fisher et al.(1971)[6]、Macaulay(1938)[28]、Willner(1996)[29]、王志强 等(2010)[30]、张继强(2004)[31]基于靜态利率期限结构的视角进行了研究,但是构建了不同类型的测度免疫方法,在不同程度上发展了投资免疫理论。Ingersoll et al.(1978)[32]、王克明 等(2010)[33]、曾黎(2010)[34]、朱峰(2013)[35]依托现代利率期限结构理论,构建了极有实用价值的随机测度免疫方法。
一般而言,可以把债券投资组合面临的利率风险分为因债券利率变动导致的价格变动风险和所获得的利息收入的再投资风险。当利率上升时,利息收入的再投资收益率会上升,同时又会导致债券价格下跌,而使得组合价值遭受损失;反之,当利率下降时,债券价格会上涨,使得债券组合的价值增值,但会引起利息收入的再投资收益率下降。可见,价格变动或再投资收益变动会引起债券组合价值的反向变动。因此,可以设定某种利率风险免疫管理策略来使得两者相互抵销、对冲,使利率波动不会影响债券投资组合的价值。
研究发现,可以利用更加复杂的久期度量方法,使其充分反映利率期限结构变动中的非线性特征,或者说利用久期向量来反映影响期限结构变化的各种风险因子。为了免疫利率期限结构的非平行移动风险,Fong et al.(1984)[4]通过利用模型对计划投资期内债券组合现金流的变异程度极小化,其模型为:
■M2p=■wiM2i
M2i=∑t(Ni)t=t(1)(t-H)2ctP(t)/Bi0
s.t.■wiDi=H
■wi=1(1)
其中,wi为持有第i个债券的权重,Ni为第i个债券的剩余付息次数,t(·)为付息日距构建投资组合时点的期间,H为组合计划持有期间,ct为t时期的现金流,P(t)为折现函数,Bi0为第i个债券的剩余现值,Di为第i个债券久期。
M2模型对久期免疫策略进行了改进,在一定程度上摆脱了对利率期限结构水平变动的假设,可是模型却无法对更复杂的收益率曲线扭曲变动形式进行免疫。但在此基础上,Nawalkha et al.(1997)[36]将M2拓展为M-Vector模型。债券组合终值的变化表示为[37]:
由公式(5)和(6)可知,参数Mm和Xm决定了债券投资组合终值变化幅度的大小。Mm取决于投资期限H,可以在配置组合时进行设定;而Xm则仅是期限H定义的期限结构变动参数。为了使利率波动不影响债券投资组合的价值,设定Mm=0(m=1,2,…Q),也就是M-Vector为零向量。当Q=1时,M-Vector简化为传统的久期免疫;当Q=2时,M-Vector简化为M2模型。
四、银行间的国债收益率曲线变动特征
由于利率是债券风险的主要驱动因素,因此构建免疫组合就需要研究利率期限结构的变动特征。国外学者针对利率期限结构进行了大量的实证研究,比较一致的看法是,对利率变动总体方差的绝大部分贡献归功于两个或者三个因子。比较典型的是Littennant et al.(1991)[9]的研究成果,他们认为驱动收益率曲线变动的三个主要因素是水平因素、倾斜因素和曲率因素。进一步可知,研究利率免疫策略实际上就是寻求债券的最佳组合。
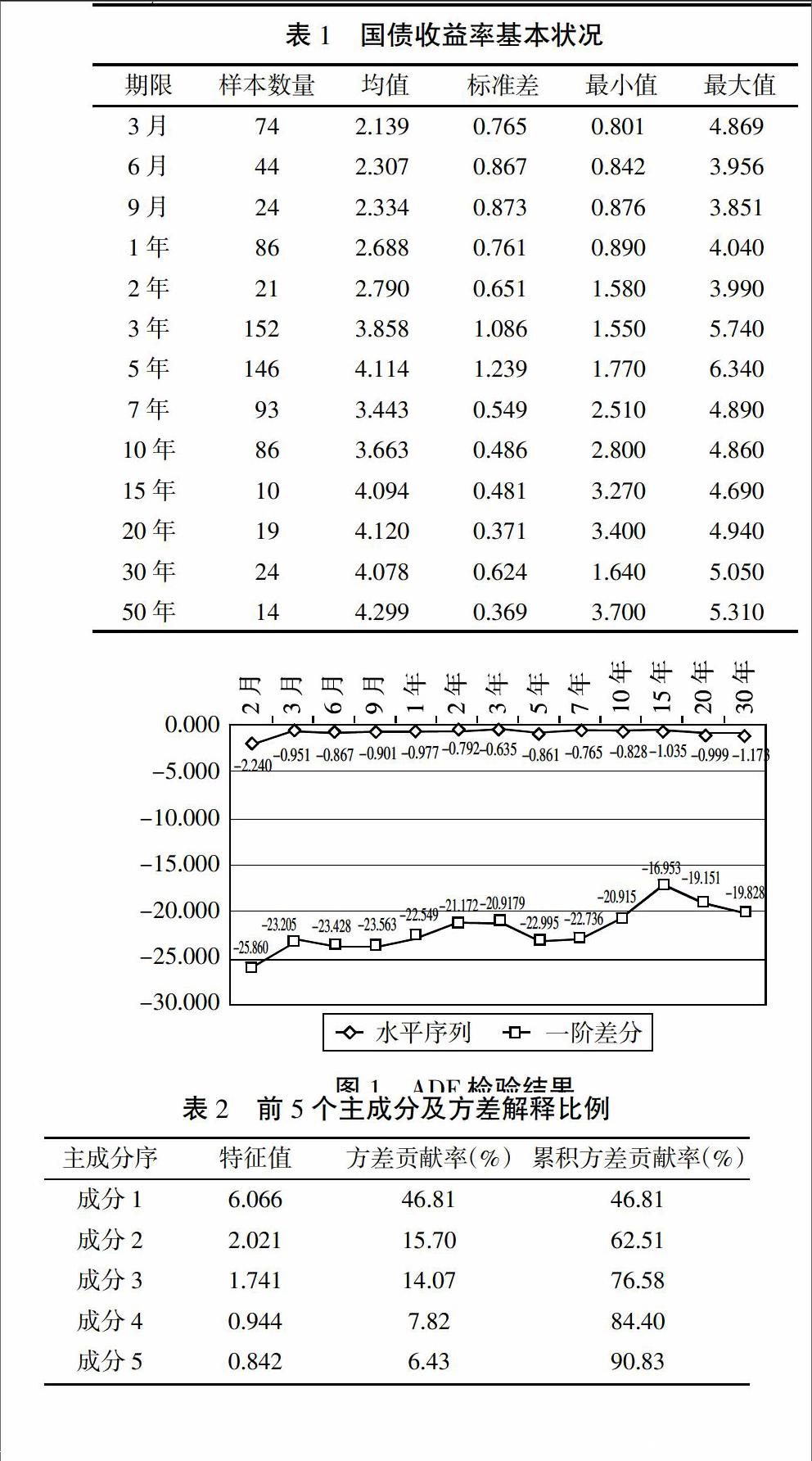
1. 国债收益率的基本特征。本文使用主成分分析法识别和分析收益率曲线的变动因素。我国银行间债券市场主要以国债、央票和政策性银行债为主,其中国债的流动性相对较高,因此将主要使用国债利率期限结构数据进行主成分分析。统计分析我国过去发行的国债,按照利率结构划分可以发现固定利率占大部分,浮动利率的相对较少。因此,样本选取银行间固定利率国债,样本数据选取2003年1月1日至2016年6月30日的数据。但是,由于银行间债券收益率容易受到极端事件的影响,为了避免收益率极端值对研究结果的干扰,并保留利率期限结构变动的主要特征信息,样本数据中剔除1%样本分位数以下的数据。最终,选定13个标准期限793个样本数据作为研究对象,每个期限的样本数量、均值、标准差、最大值、最小值如表1所示。
从样本总体上看,银行间国债利率期限结构并非呈现平坦化形态,而是呈现出一定的向上倾斜趋势,各个收益率的波动性也出现一定的差异,这说明可能存在多种不同的因素影响收益率曲线的变动,不同因素对期限收益率的影响不同。
一般而言,宏观经济变量通常具有水平增长趋势特征,若直接使用变量值进行相关性或回归分析,则会造成高度相关或伪回归的结果,很难或者无法得到变量之间真正的变动关系。现实经济社会中,利率是重要的宏观经济变量之一,利率变动大多存在着趋势特征,因此需要进行单位根检验[38]。从ADF的检验结果(图1)可以看出,13个期限的收益率水平时间序列显示出较为明显的非平稳特征,都没有通过10%的显著水平检验;可是这13个期限的全部一阶差分时间序列均呈现出较为平稳的特性。由此可知,进行主成分分析,应剔除趋势因素对收益率的固有影响,因此,本文中采用收益率的一阶差分(即收益率日变化量)数据进行主成分分析。
2. 收益率曲线变动的主要影响因素分析。主成分分析(表2)显示,从对收益率方差的贡献率来看,三个主要因素占比分别为水平因素占46.81%、倾斜因素占15.70%、曲率因素占14.07%,三个因素对方差的累计解释能力仅占76.58%。从这些数据可以看出,我国银行间市场的利率期限结构与前文分析的已有实证结果之间存在很大差异。虽然采用国外数据和国内数据进行的实证研究均显示水平因素在利率期限结构变动中占主导地位,倾斜因素和曲率因素占第二、第三位,从定性分析上一致。与国外市场相比,三个因素对银行间市场的影响力相比较弱,第四个主成分的方差贡献比达到7.82%,前五个主成分可以达到90%。但是,基本上述5个主成分因子可以刻画银行间市场国债利率期限结构的变化特征。
进一步分析,由于每个特征向量都独立影响利率曲线运行,同时,实证研究分析可以得出,影响银行间国债收益率曲线变动的因素比较复杂。国内外分析相比,成分1水平因素在国外市场可以影响收益率曲线变动的70%以上,而在我国的影响力不足50%;成分2倾斜因素在国外市场通常具有20%以上,而在我国的影响力不足16%;成分3曲率因素在国外市场通常只具有5%的解释力,但在国内却达到了14.07%;在国内,第4、5成分的特征向量代表的驱动因素的解释合计约14%左右。因此,在我国前两个主成分(水平因素与倾斜因素)对国债收益率曲线影响不足63%,则说明不可忽略其他更复杂因素对收益率的影响。
由前文可知,商业银行在银行间债券市场中占主导地位,投资主体的同质化容易形成相同的交易倾向而造成市场交易过度向局部进行集中,从而增加了收益率变化的复杂性。同时,由于国有商业银行的市场影响力更为巨大,因此个别交易产生的随机影响对于收益率曲线的影响也较为明显,进而造成形态更为复杂的变动因子的出现,如第四个和第五个特征向量所示曲线变动形态。
从主成分分析的结果来看,主要有五个驱动因素影响着我国银行间国债收益率曲线,其对收益率方差的累积解释力为90.72%①。而水平因素与倾斜因素对于收益率曲线的变动解释力仅有62%。因此,如果仅仅使用久期匹配模型用于构建利率免疫投资组合,那么有可能得到较差的效果;而曲率及其他更复杂的驱动因素的影响不可忽视(30%以上的解释力),因此需要使用更复杂的免疫策略来对冲,从而达到更佳的保值效果。通常为了规避利率风险,可以采用M-vector模型构建不同的投资组合来规避风险。
五、基于M-vector模型的多维久期配比免疫策略分析
1. 实证研究设计。本文构造利率免疫投资组合来规避利率风险,其目标是旨在计划持有投资期间内锁定对应期限的收益率,或者说利率期限结构变动不影响目标收益率②。
(1)免疫策略的选择。根据前文的主成分分析结果,可以发现影响国债收益率曲线的变动因素较多,通常的久期配比免疫策略可能难以起到较好的效果。因此,本文使用多维久期配比策略来对这些变动因素进行免疫,主要利用M-Vector模型来实现。在实证分析中使用以下五种约束条件来实现免疫策略:
Macauly久期,Dmac=H;
M-vector的前两个元素,Mm=0,m=1,2;
M-vector的前三个元素,Mm=0,m=1,2,3;
M-vector的前四个元素,Mm=0,m=1,2,3,4;
M-vector的前五个元素,Mm=0,m=1,2,3,4,5。
(2)持有期间的设定。结合本文所取得的数据资料,考虑到要对债券组合的免疫效果进行实际比较,为了增加观测时点数量,在样本期间内连续观察构造的投资组合,從研究样本初期,每个季度末构建债券组合并评价其表现。由此可以得到每个策略组合的54个观测点,从而在一定程度上避免随机因素对投资组合表现的影响。
(3)组合的优化模型设计。构建投资组合采用二次规划模型(公式7),目标函数设定为最小化交易额,也等同于最小化交易成本③,采用Macaulay久期匹配策略进行投资组合。
其中,pi为第i支债券的价格;ni为持有第i支债券数量,可以看作模型的决策变量;N为免疫组合的债券品种数量;wi=nipi/I0为免疫组合中某种债券占比;为免疫组合的投资数额。I0为简化计算,假设可以无限分割债券数量,也就是债券交易没有最小数量的限制。
(4)衡量免疫效果的指标。
未免疫比率指标,设定为未超过目标收益率次数与总观察次数的占比。
Fishburn风险度量指标:
其中,k=1,…,5为待考察的5种免疫策略;N为持有期间内对组合免疫的总观察次数;rj为第j组合在持有期间的年收益率;Rj(0,t)为第j组合中当日剩余期限为t的即期收益率;∑{r j,k RMSE和MAE指标,将组合持有期初的收益率曲线对应期限的收益率作为目标收益率,误差RMSE和MAE分别定义为: 2. 免疫策略效果分析。一方面,从各个组合的持有期收益率(图2)来看,使用免疫策略均获得了较高的组合收益水平,同时收益率的稳定性也较好。各免疫策略组合的标准差均低于基准组合的标准差2.26%;各免疫策略组合的平均收益率均高于基准组合的平均收益率1.76%;各种免疫策略之间收益率差异也较大,MV3组合达到最高3.73%。 综上所述,可知采用多维久期约束策略比传统的Macaulay久期约束策略表现更好,意味着除水平因素外,倾斜因素和曲率因素对银行间国债利率期限结构的影响也很明显,因此,免疫效果依靠单一的久期约束策略无法完全实现。 另一方面,从各项免疫效果度量指标(表3)来看,各项免疫策略的表现有所差异,从未免疫次数来看,基准组合的表现并不完全比免疫组合差,甚至好于Mac、MV4和MV5组合;MV2和MV3组合均明显优于其他免疫组合,其中MV3组合免疫效果最佳。从Fishburn、RMSE和MAE度量指标都可以看出,基准组合呈现出较大的波动性;免疫组合的效果优于基准组合,即免疫组合的持有期收益率接近于目标收益率;MV3组合的RMSE和MAE指标较高,且其未免疫率最低,可知其高于目标收益率的幅度较大,在最大化免疫效果的同时保证了较高的收益率。
六、总结
综上所述,我国债券市场与其他国家债券市场相比,我国国债收益率曲线变动的因素较为复杂,水平因素、倾斜因素和曲率因素具有的影响力以及三者之和的影响力均低于其他国家。传统的久期匹配策略难以对投资组合的利率风险起到较好的免疫效果,需要增加更多的约束条件来实现对倾斜和曲率等因素进行匹配对冲。
由于我国银行间债券市场的独特特性,例如市场投资者行为的趋同性、交易方式的单一性等,使影响收益率曲线变动的因素较为复杂,造成构建利率免疫组合的过程较为复杂。然而,随着我国债券市场的进一步发展完善,会形成较为完整和统一的收益率曲线,使得水平因素对其变动主导性作用加强,此时久期免疫策略的效果就会大大增强。
因此,在我国的现实环境中,投资者可根据自身的风险偏好,动态地对收益率曲线进行考察,从而选择合适的免疫策略构造投资组合模型,通过对影响不同期限债券的关键宏观经济变量的分析与预判调整组合久期,从而实现收益与风险之间的平衡。
注释:
①国内其他学者利用交易所国债数据的分析结果表明,水平因素、倾斜因素与曲率因素等的解释力达90%以上(朱峰,2004),由此可知,银行间债券市场的利率变动特性较为复杂。
②一般地,对负债现金流较难进行预测,同时由于我国还缺乏较为统一、完整的基准利率期限结构体系,使得对负债的免疫策略较难构造。
③构建组合时交易成本是重要的考虑因素,一般而言,交易成本与交易额存在正比关系,这里为简便起见,用交易额来替代交易成本作为目标函数。此外,二次函数形式有助于求唯一解,故目标函数未采用线性形式。
参考文献:
[1]MARKOWITZ H. Portfolio selection[J].Journal of finance,1952,7(1):77-91.
[2]BIEEWAG G O ,KAUFMAN G K ,TOEVS A. Immunization strategies for funding multiple liabilities[J].Journal of financialand quantitative analysis,1983 (3):113-124.
[3]FISHER L,WEIL R.Coping with the risk of interest-rate fluctuations:returns to bondholders from naive and optimal strategies[J].Journal of business,1971(44):408-431.
[4]FONG H,VASICEK O. Risk minimizing strategy for portfolio immunization[J].The journal of finance,1984 (39):1541-1546.
[5]BARRETT WB,HEUSON A J,GOSNELL T F.Yield curve shifts and the selecton of immunization strategies[J].Journal of fixed income,1995(5):53-64.
[6]HO T.Key rate durations:measures of interest rate risks[J].Journal of fixed income,1992 (2):29-44.
[7]Sundaresan S M.Fixed income markets and their derivatives[M].Secondedition,South-Western College Publishing,2002.
[8]DIEBOLD F X ,LI C. Forecasting the term structure of government bond yields[J].Journal of econometrics,2006(130):337- 364.
[9]LITTERMAN R,SCHEINKMAN J.Common factors affecting bond returns[J].Journal of fixed income,1991(1):54-62.
[10]MARIDA B,ROSELLA G,STAVROS A Z.Risk factor analysis and portfolio immunization in the corporate bond market[J].European journal of operational research,2005(161):348-363.
[11]SOTO G M. Duration models and IRR management:a question of dimensions[J].Journal of banking and finance,2004,28 (5):1089-1110.
[12]陳雯,陈浪南.国债利率期限结构:建模与实证[J].世界经济,2002(8):15-23.
[13]郭涛,李俊霖.利率期限结构曲线的估计方法[J].南方经济,2007(12):63-72.
[14]宋逢明,石峰.基于Hull-White模型的债券市场利率期限结构研究[J].运筹与管理,2006,15(3):85-89.
[15]杨大楷,杨勇.关于我国国债收益率曲线的研究[J].财经研究,1997(7):14-19.
[16]姚长辉,梁跃军.我国国债收益率曲线的实证研究[J].金融研究,1998(8):12-18.
[17]朱世武,陈健恒.交易所国债利率期限结构实证研究[J].金融研究,2003(10):22-28.
[18]周荣喜,邱菀华.基于多项式样条函数的利率期限结构模型实证比较[J].系统工程,2004(6):17-25.
[19]周荣喜,邱菀华.BDT模型的扩展及应用研究[J].数量经济技术经济研究,2005(2):34-40.
[20]周子康,王宁,杨衡.中国国债利率期限结构模型研究与实证分析[J].金融研究,2008(3):131-150.
[21]王实,赵振全,王勇.债券投资组合分析方法及随机规划应用的探讨[J].吉林大学社会科学学报,1996(5):22-26.
[22]黄兴,张维.商业银行债券投资组合的优化模型[J].天津大学学报:社会科学版,2000,2(3):183-186.
[23]朱世武,李豫,董乐.交易所债券组合动态套期保值策略研究[J].金融研究,2004(9):65-76.
[24]刘琳琳.债券投资组合利率风险管理的久期免疫策略[J].科技与经济,2006(20):30-31.
[25]唐革榕,朱峰.我国国债收益率曲线变动模式及组合投资策略研究[J].金融研究,2003(11):64-72.
[26]刘川巍.我国商业银行债券资产利率风险的控制与管理[J].上海金融,2004(9):22-24.
[27]王志强,张皎.久期配比策略的免疫性分析——来自中国国债市场的经验证据[J].财经问题研究,2009(11):48-51.
[28]MACAULAY F.Some theoretical problems suggested by the movements of interest rates,bond yields,and stock prices in the united states since 1856[R].New York:national bureau of economic research working paper,1938:1-15.
[29]WILLNER R.A new tool for portfolio managers:level,slope,and curvature durations[J].The journal of fixed income,1996(8):48-59.
[30]王志強,康书隆.Nelson-Siegel久期配比免疫模型的改进与完善[J].数量经济技术经济研究,2010(12):133-147.
[31]张继强.债券利率风险管理的三因素模型[J].数量经济技术经济研究,2004(1):62-67.
[32]INGERSOLL J E,SKELTON J,WEILR.Duration forty years later[J].Journal of Financial and Quantitative Analysis,1978,13(4):627-650.
[33]王克明,梁戍.基于利率期限结构的随机久期与凸度模型构建及应用[J].统计与决策,2010(24):158-160.
[34]曾黎.基于违约风险的Vasicek利率风险研究[J].数学理论与应用,2010,30(1):67-70.
[35]朱峰.Vasicek方向久期:一类新的利率风险免疫工具[J].金融监管研究,2013(1):69-79.
[36]NAWALKHA S K,CHAMBERS D R.The M-vector model:derivation and testingof extensions to M-square[J].The journal of portfolio management,1997(12):92-98.
[37]朱峰.国债利率风险免疫策略研究[D].厦门:厦门大学,2004.
[38]LEKKOS ILIAS. A critique of factor analysis of interest rate[J].Journal of Derivatives,2000(9):72-83.
责任编辑:关 华

