从2016年高考新课标Ⅰ第16题谈“等效电阻法”的应用
唐王雅斌 陈笃杰
(漳州市第三中学 福建 漳州 363000)
从2016年高考新课标Ⅰ第16题谈“等效电阻法”的应用
唐王雅斌 陈笃杰
(漳州市第三中学 福建 漳州 363000)
针对考生在解答2016年高考全国新课标Ⅰ卷第16题时,常规的解法存在着推导繁琐和计算量大等困难,通过介绍变压器的“等效变阻法”并尝试应用该方法解题,化繁为简,起到事半功倍的效果.
等效电阻 理想变压器 简化电路
2016年高考全国新课标Ⅰ卷理综第16题考查了理想变压器的知识,《考试说明》对理想变压器掌握程度的要求为Ⅱ级,要求考生应对这个考点,不仅要做到理解,而且要能够解决实际的应用问题.不少考生应用基本电压、电流比的关系进行求解,遇到大量繁琐的数学推导和计算,有些考生算不出来功亏一篑,有些考生费尽周折最终选了正确选项,却浪费了宝贵的考试时间.为此,我们针对变压器问题寻求简化的思路和多种解法,现就本试题进行探讨.
1 试题原题和命题分析
【题目】一含有理想变压器的电路如图1所示,图中电阻R1,R2和R3的阻值分别为3 Ω ,1 Ω ,4 Ω,○A为理想交流电流表,U为正弦交流电压源,输出电压的有效值恒定.当开关S断开时,电流表的示数为I;当S闭合时,电流表的示数为4I.该变压器原、副线圈匝数比为( )
A.2 B.3 C.4 D.5
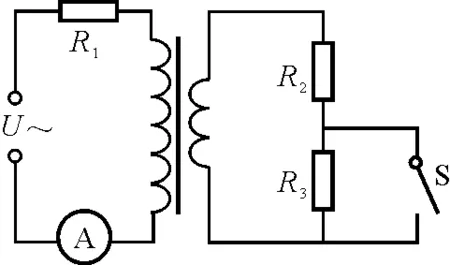
图1 含有理想变压器的电路图
本题的正确选项为B.
命题分析:本题考查理想变压器副线圈负载动态变化情况下,原副线圈电压电流与匝数比关系的一道应用题.难点在于原线圈接入一电阻使原线圈电压不等于电源电压U,且原线圈两端电压也随电流变化而变化,开关S闭合前后原副线圈的电压和电流全都改变,只有匝数比不变.本题在考查学生对理想变压器基础知识掌握的同时,也对学生的数学运算能力有一定的要求;同时要求考生在解题时,按开关断开和闭合两种情况有条不紊地进行分析,突出了对考生分析综合能力的考查.
2 两种常规解法
解法一:电压、电流和匝数比关系
当S断开时,R2和R3串联,因为R1和原线圈是串联关系,所以原线圈两端电压为
U1=U-IR1
即
U1=U-3I
(1)
由原副线圈电压和匝数比关系
(2)
又原副线圈电流和匝数比关系
(3)
副线圈中的电流
(4)
联立式(1)~(4)得
(5)
当S闭合时,R3被短路,因为R1和原线圈串联,所以原线圈两端电压为
即
(6)
由原副线圈电压和匝数比关系
(7)
又原副线圈电流和匝数比关系
(8)
副线圈中的电流得
(9)
联立式(5)~(8)得
(10)
联立式(5)、(10)解得
解法二:理想变压器输入输出电能守恒
当S断开时,因电源的总功率等于各个电阻消耗的功率之和有
即
(11)
原副线圈电流和匝数比关系为
(12)
联立式(11)、(12)得
(13)
当S闭合时,因电源的总功率等于各个电阻消耗的功率之和有
即
(14)
原副线圈电流和匝数比关系
(15)
联立式(14)、(15)得
(16)
联立式(13)、(16)解得
3 理想变压器“等效电阻法”介绍和在本题中的应用
问题:一理想变压器的原、副线圈匝数比为n1:n2,副线圈接一负载电阻,阻值为R,如图2(a)所示,求:当理想变压器正常工作时,ab之间虚线框内的等效电阻R′为多大?
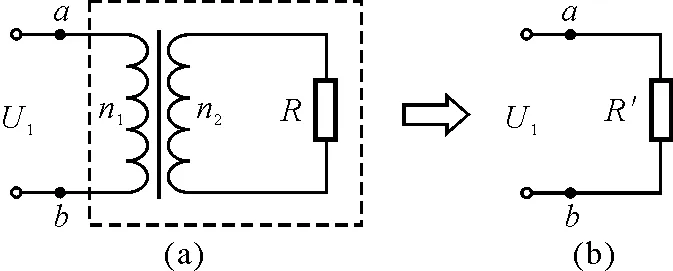
图2 理想变压器等效电阻变换
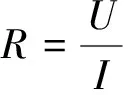
由于
且
联立以上各式得
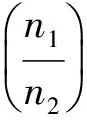
意义:电工技术中可利用变压器这一关系实现交流电路的“阻抗匹配”,改变负载电阻R或采用不同的线圈匝数比,以达到增大或减小总负载阻抗的目的,使之变换为所需要的、比较合适的数值.
应用:该方法解析2016年高考新课标Ⅰ卷理综第16题.
解法三:等效电阻法
当S断开时,R2和R3串联,如图3虚线内的部分即ab之间的等效电阻R′.
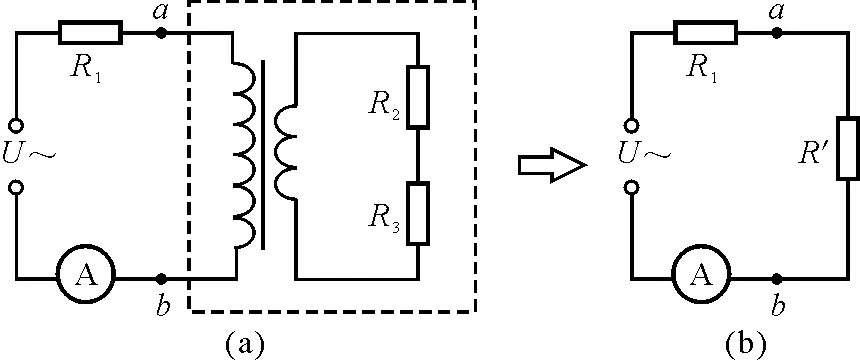
图3 R2和R3串联时,理想变压器的等效电阻变换
等效电阻
(17)
由闭合电路欧姆定律,电流表示数
(18)
式(17)代入式(18)得
(19)
当S闭合时,R3被短路,如图4虚线内的部分即ab之间的等效电阻R″.
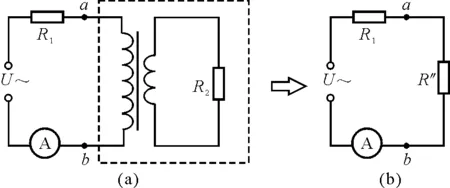
图4 R3被短路时,理想变压器等效电阻的变换
等效电阻
(20)
由闭合电路欧姆定律,电流表示数
(21)
式(20)代入式(21)得
(22)
联立式(19)、(22)解得
4 3种解法比较
区别:解法一应该是学生在解决变压器问题时最常用、最基本的方法,然而题中所列方程数多达10个,联立整合后计算量偏大,似乎更侧重于考查数学能力,学生在紧张的高考氛围中,容易出错且费时费力;解法二利用理想变压器电能守恒也属于常规解法,相对而言是简便了一些,但较少有学生会用能量观点来思考问题,在使用焦耳定律计算电功率时电流的平方容易疏忽,仍有一定的计算量;解法三应用“等效电阻法”把变压器原、副线圈的两个回路巧妙地转换为一个回路来处理,简化成学生最熟悉的闭合电路欧姆定律模型,使解题思路豁然开朗,推导和计算也变得简洁准确,同时该解法更多地侧重于物理思想的应用,在解决复杂的变压器交流电路问题时不仅可以“化繁为简”,而且从知识本质上赋予了更多的物理意义.
联系:其实3种解法殊途同归,例如,当S断开时,解法一中若暂不代入电阻阻值,式(5)可表示为
变形得
对照解法三中的式(18)
其中
我们发现常规解法和“等效电阻法”可以互推,虽然不同解法的切入点和过程不同,但结果和物理本质却是相同的.
5 结束语
在高考中偶尔会出现个别试题,可以用大学普通物理的内容巧妙地解答.在中学阶段“等效电阻法”可作为理想变压器教学的一种延伸,让学生知道变压器不仅可变电压、变电流,还可通过“变电阻”简化电路,便捷地解题.建议在处理含理想变压器的交流电路问题中进行介绍和拓展,不能简单地把“等效电阻法”看成只是一种解题技巧,用好该方法既有利于学生深入理解变压器的原理和完善系统知识结构,也有助于培养学生“等效转换”的物理思想,也从而提升此类问题的解题能力.
1 教育部考试中心.2016年普通高等学校招生全国统一考试大纲的说明(理科).北京:高等教育出版社,2016.285
2 2016年全国普通高等学校招生全国统一考试理科综合能力测试(新课标Ⅰ卷)物理试题,2016.6
3 秦曾煌.电工学(第六版)上册.北京:高等教育出版社,2004. 188
4 陈炳龙.变压器的变阻规律及应用.中学物理教学参考,2002,31(6):23~24

2016-06-28)

