电容器能量的3种求法*

郑世燕*

(泉州师范学院物理与信息工程学院 福建 泉州 362000；淡江大学物理系 台湾 新北 25137)

电容器能量的3种求法*

郑世燕*

(泉州师范学院物理与信息工程学院 福建 泉州 362000；淡江大学物理系 台湾 新北 25137)

分别利用电容器的能量公式、电场的能量公式以及电荷系的静电能公式求出一般电容器所储存的能量．

电容器能量 电场能量 静电能

电容器是一种容纳电荷的器件．任何两个彼此绝缘且相隔很近的导体(包括导线)间都构成一个电容器，对一个孤立导体也可以认为它和无限远处的另一导体组成一个电容器[1，2]．电容器带电时具有能量，文献[1]和[2]中给出电容器的能量是它充电时由电源供给的，进而得到电容器的能量公式为

(1)

式中W，Q，U及C分别表示电容器的能量、所带的电荷量、相应的电压及电容．

以平行板电容器为例，电容器的能量也可认为是储存在电容器内的电场之中，即电场的能量

(2)

式中we，V，ε0，εr，ε，D及E分别表示电场的能量体密度、电容器的体积、真空中的电容率、相对电容率、电容率、电位移矢量及电场强度．

本文在平行板电容器的基础上将进一步把上述公式应用到一般电容器，如：球形电容器、圆柱形电容器及孤立导体电容器等．文中还将从电荷系的静电能公式[1]

(3)

给出求解一般电容器能量的第三种方法．上式中q及φ分别表示电容器所带的电荷量及两极板各自的电势．

1 平行板电容器

如图1所示，该平行板电容器的正对面积为S，两极板间距为d，板间充满相对介电常量为εr的电介质，所带电荷量为Q.

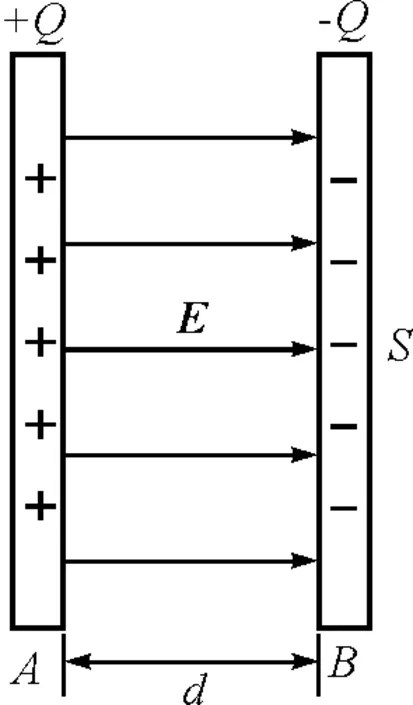
图1 平行板电容器

(4)

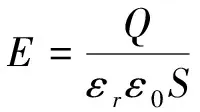
(5)

则由公式(1)及(4)可得出平行板电容器的能量为

(6)

由公式(2)及(5)也可得到平行板电容器的能量为

(7)

最后由公式(3)，同样可得到平行板电容器的能量为

(8)

显然，3种方法得到的结果是一致的．

2 球形电容器

一球形电容器如图2所示，其内外球的半径分别为R1和R2，两球间充满相对介电常量为εr的电介质.

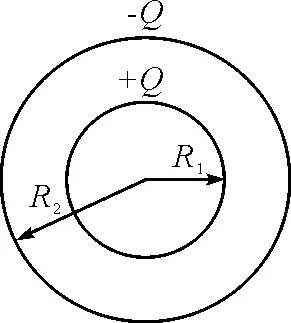
图2 球形电容器

其电容为

(9)

当电容器带有电荷量Q时，根据高斯定律可得两板间的电场强度为

(10)

两极板间的电势差为

(11)

此时，可用与上面类似的方法求出带有电荷量Q的球形电容器所储存的能量分别为

(12)

(13)

(14)

3 圆柱形电容器

一高度为l的同轴圆柱形电容器半径分别为R1和R2，如图3所示，两极板间充满相对介电常量为εr的电介质.

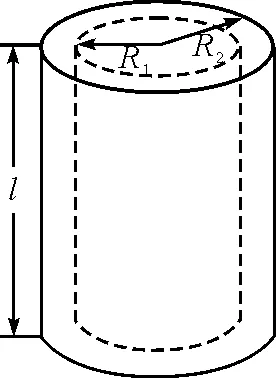
图3 圆柱形电容器

其电容为

(15)

当电容器带有电荷量Q时，两板间的电场强度为

(16)

两极板间的电势差为

(17)

同理可求出带有电荷量Q的圆柱形电容器所储存的能量分别为

(18)

(19)

(20)

4 孤立导体电容器

以一个在充满相对介电常量为εr的电介质空间中的半径为R的孤立导体球面(带电荷量为Q)为例，其电容为

(21)

周围空间的电场强度为

(22)

电量所在处的电势为

(23)

同理根据公式(1)～(3)及公式(21)～(23)可分别求出孤立带电球面电容器的能量如下

(24)

(25)

(26)

5 结束语

通过以上推导，可以清晰看到公式(1)～(3)分别以电容、电场强度及电势为主要物理量求出一般电容器所储存能量的3种求法．在解题中可根据具体已知条件而运用相应的公式求解，这对于提高学生解题能力是有益的．

1 张三慧. 大学基础物理学(第二版 下册).北京: 清华大学出版社,2007

2 赵凯华，陈熙谋. 电磁学(第二版 上册).北京: 高等教育出版社,1998

ThreeMethodsforCalculatingtheCapacitorEnergy

Zheng Shiyan

[CollegeofPhysicsandInformationEngineering,QuanzhouNormalUniversity,Quanzhou,Fujian362000;DepartmentofPhysics,TamkangUniversity,NewTaipeiCity25137,Taiwan(R.O.C.) ]

By using the energy formula of capacitor,the energy formula of electric field and the electrostatic energy formula of charge system, the energy stored in the capacitor is calculated.

capacitor energy;electric field energy;electrostatic energy

**泉州师范学院青年人才基金资助的课题．课题批准号：201604作者简介：郑世燕(1979- ),女,硕士,副教授,主要从事热力学统计物理方面的研究.

2016-07-13)