部分失速工况下轴流压气机转子受力特性的研究

万书亭, 豆龙江， 詹长庚

(1.华北电力大学 机械工程系，河北 保定 071003; 2.杭州汽轮机股份有限公司，杭州 310000)

部分失速工况下轴流压气机转子受力特性的研究

万书亭1, 豆龙江1， 詹长庚2

(1.华北电力大学 机械工程系，河北 保定 071003; 2.杭州汽轮机股份有限公司，杭州 310000)

首次将轴流压气机的受力特性与工况相结合，分析压气机转子的速度变化和受力特性。首先从理论角度阐述了轴流压气机的失速原理及过程，然后对压气机在正常运行工况和部分失速工况下的受力表达式进行理论推导，通过仿真得出轴流压气机在部分失速工况下的受力特性，最后将仿真结果与理论推导部分相对比。论文通过仿真验证了理论分析的可行性，并得出了失速工况下轴流压气机的速度变化与受力特性，为后续转子的振动分析以及转子的结构优化设计提供有益参考。

失速；轴流压气机；转子；受力特性

燃气轮机组以其高效洁净的优点在电力行业中占据着重要的地位，按照我国国民经济发展前景，电力工业发展需要大批量的燃气轮机，燃气轮机在国内具有较大的发展机遇与市场需求[1]。然而与燃机迅速发展相对应的，燃机的技术却一直受到国外公司的垄断，国内许多科研院所和高校对燃气轮机展开了研究。

轴流压气机作为燃气轮机的重要组成部件，对其稳定性的研究已经是燃机的关键技术之一。目前国内对轴流压气机稳定性的研究主要从失速和喘振两个方面，由于喘振故障特征剧烈事故现象较少，而失速是其诱因且发生频次高，多以对燃机轴流压气机失速的研究相对而言更有实际应用价值。Emmons最早提出了失速机理，并分析了失速的形成原因和沿流道传播的机理，指出时速团传播的速度与转速相反[2]。DAY[3]对小失速团进行了分析，得出了“小尺度扰动”理论；GREITZER等[4]提出了将临界B参数用于判断系统是否失速的观点，开创了失速喘振研究的数值模拟先河；MOORE等[5]提出了经典的MG模型，并定性提出了深度喘振和经典喘振的区别。FEULNER等[6]则考虑执行机构对模型的影响，提出了应用于旋转失速主动控制的理论模型；GRAVDAHL等[7]提出轴流压气机的包含转子动态参数的MG扩展模型；HU等[8]在文献[5]的基础上，采用了修改的模型简化方式得到便于计算机仿真的扩展MG模型。蒋康涛等[9-10]对低速轴流压气机转子进行了二维和三维的数值仿真，并得出近失速先兆特性；吴艳辉等[11-12]对轴流压气机转子在准定常和近失速工况下近叶尖流动情况进行了分析，得到了不同工况下的流场情况。

从目前研究成果看，国内对燃机轴流压气机失速研究侧重于流场分析，鲜有对轴流压气机随流场变化相应的机械结构特性分析。而机械结构是关系到生产制造的根本，并在很大程度上影响轴流压气机的使用安全和寿命，所以通过失速受力对机械结构及振动进行分析是非常有实际意义的。基于此，本文提出将流场分析与机械受力相结合的分析方式，从轴流压气机的失速出发，对在失速状态下转子的受力特性进行分析，将流体分析与转子机械结构分析相结合，得出转子在失速工况下的失速传播及受力特性，为后续转子的振动分析以及转子的结构优化设计提供有益参考。

1 轴流压气机失速原理与引发条件

1.1 压气机失速原理

轴流压气机在工作中，转子按照一定的转速旋转，流体在流经转子流域时受到转子叶片的作用力而发生速度的变化。当压气机转子工作在非稳定区域内，内部流体会出现一定的扰动，进而形成失速。

轴流压气机叶栅中出现旋转失速情况如图1所示。

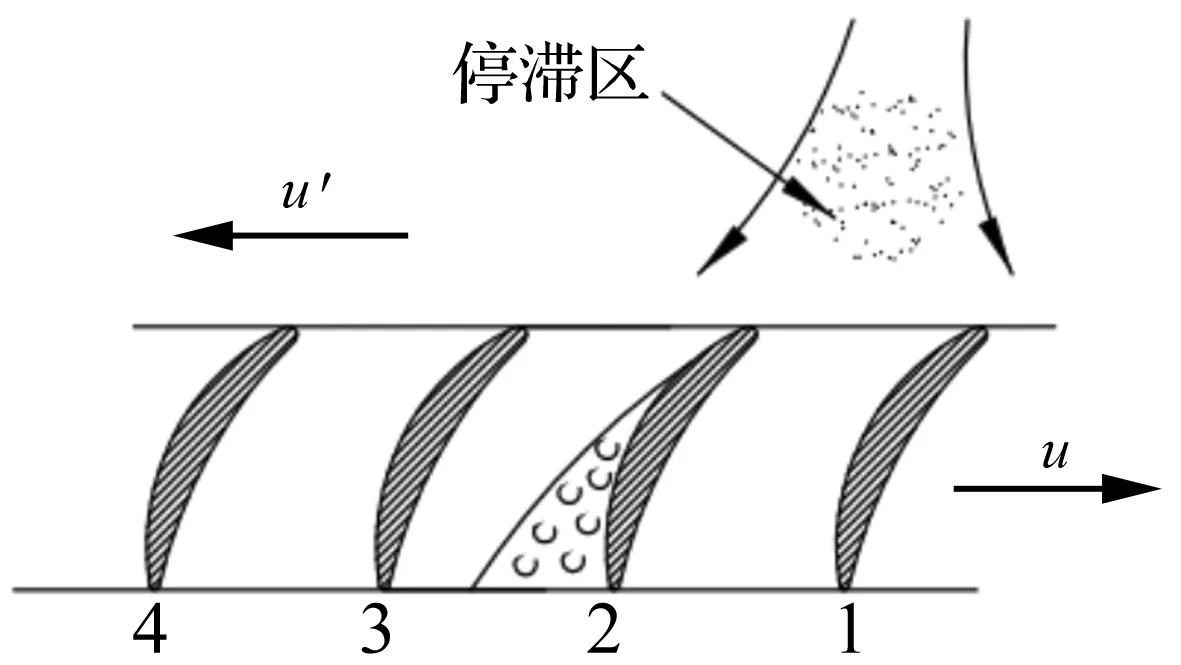
图1 压气机旋转失速过程Fig.1 The rotating stall process of axial compressor

轴流压气机的动叶栅以u的旋转速度向右运动，由于运行过程中的扰动，首先在叶片2的背弧面上出现了气流脱离现象；这时在叶片2和叶片3之间的气流通道会因为这部分脱离气流的影响，导致部分堵塞。堵塞通道进口的部分将形成低速流区，该区域受后续气流的影响迫使附近的气流逐渐改变原先的流动方向，使停滞区右侧的气流冲角减小；进而叶片1的绕流情况得到改善，气流脱离现象将逐渐缓解，同时受低速流区的影响，叶片3的背弧侧开始发生气流脱离现象。这样旋转失速就从叶片2开始向叶片3转移。

1.2 压气机失速引发条件

轴流压气机运行中在不考虑温度的情况下，转速、流量和压比三者须满足一定的关系，轴流压气机才能稳定的运行。对于特定的轴流压气机，这三者的关系可以在坐标图中表示，称之为特性曲线，如图2所示。

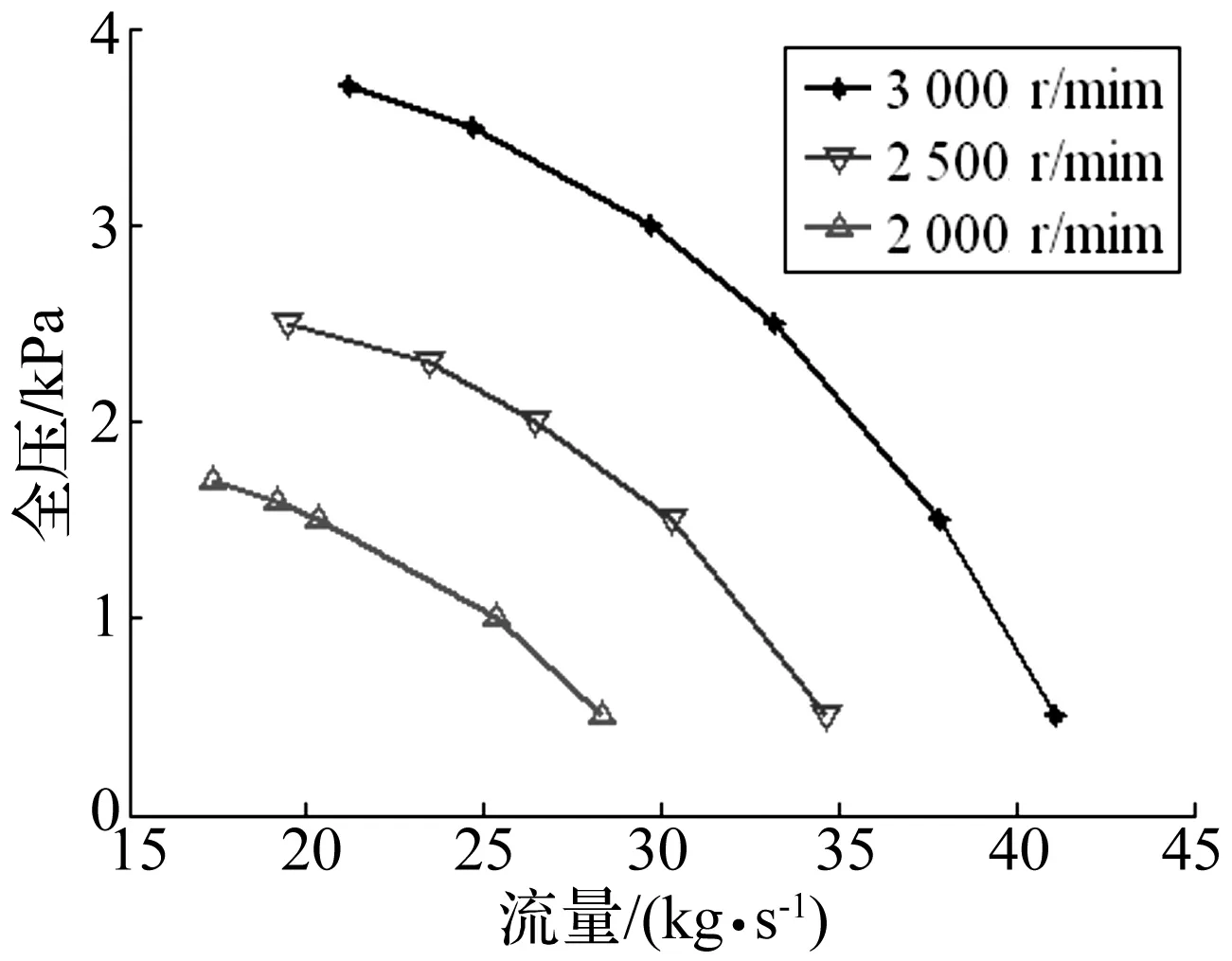
图2 轴流压气机的特性曲线Fig.2 The characteristic curves of axial compressor

根据压气机工作特性曲线，本文按照失速的引发条件，将其分为流量变化失速和转速变化失速两类：

(1)流量变化失速

流量变化失速指的是在定转速下由于流量的变化导致失速的发生。如图2中的某条曲线，当轴流压气机运行稳定时，转速恒定的情况下如果流量发生突变，而压气机的背压受后续容器的影响不能发生突变，那么压气机将偏离原本的稳定工况，通过调整逐步向稳定点靠近。但当压气机无法使得流量变化与背压满足设计工况，那么轴流压气机将进入失速区，甚至发生喘振。这种情况在燃气轮机组使用过程中，入口发生堵塞或者气流不均匀等情况下容易发生。

(2)转速变化失速

与流量一样，转速变化失速指的是外部通流情况一定，当转速发生变化时，轴流压气机工作点随之发生的变化，内部流场由稳定向失速部分靠近。当转速发生变化时，压气机背压不能发生突变，导致实际运行工况不能工作在稳定线上，这时轴流压气机将通过入口流量的变化来保证系统的稳定运行，但是当压气机无法使得流量与转速和背压相匹配时，压气机将进入失速和喘振区。这种转速变化的引发条件常见在燃汽轮机组启停过程中。

针对这两种失速引发条件，本文的模拟主要采用的是在一定的转速下，通过控制流量和背压的关系进行失速的模拟仿真。

2 轴流压气机模型与失速受力分析

2.1 压气机转子模型

本文研究的是单级轴流压气机，其动叶转子入口处轮毂半径0.2 m，叶片轮廓外径0.4 m，叶片数18，宽度0.1 m，轴向进气。具体实体结构和叶片叶型如图3所示。为让计算更接近实际情况，在轴流压气机动叶出入口加入进出口管，叶顶间隙设置为5 mm，生成流域时，对压气机按实际尺寸划分网格，网格总数约320万。

图3 动叶及叶片模型Fig.3 The rotor and blade model

2.2 压气机失速受力分析

根据压气机失速原理，以地面为参考系，那么失速区域的运动方向与转子叶栅旋转方向一致，假设失速区域的运动速度为u′，那么

u′=k×u

(1)

式中:k为转速比，u为转子转速。若轴流压气机某个部位发生旋转失速，那么失速区会导致两动叶栅间流体流速的变化。

压气机在稳定工作时，根据动量定理单个叶片的受力可简化为：

Fui=Q/N×(c2u-c1u)

(2)

式中Q为流量，N为叶片数，c2u和c1u分别表示入口和出口的切向速度。由于叶片呈圆周均匀分布，动叶整体对外不呈现切向力。但是发生失速时，这个平衡将被打破，假设某个部位出现失速区时，该失速过程中的受力分析如图4所示。

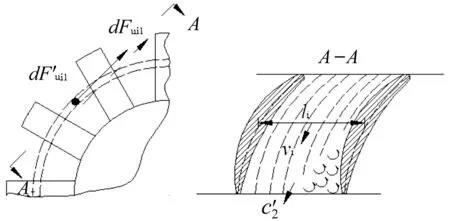
图4 失速区受力Fig.4 The force acted on the stall area of axial compressor

当A-A处发生旋转失速，该处两动叶栅间的气体微元受力较其他部位发生变化。根据受力平衡知识，轴流压气机动叶在起始受力均匀状态到不均匀状态的根本原因是因为发生旋转失速，那么：

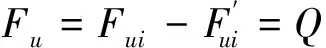
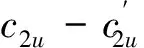
(3)

式(3)说明动叶栅在发生旋转失速时，动叶栅的切向力跟发生旋转失速前后的出口速度的变化成正比。

动叶栅在随着和转子旋转的过程中，发生旋转失速的位置以失速传播的速度发生着方向的变化。转子的受力分析如图5所示。

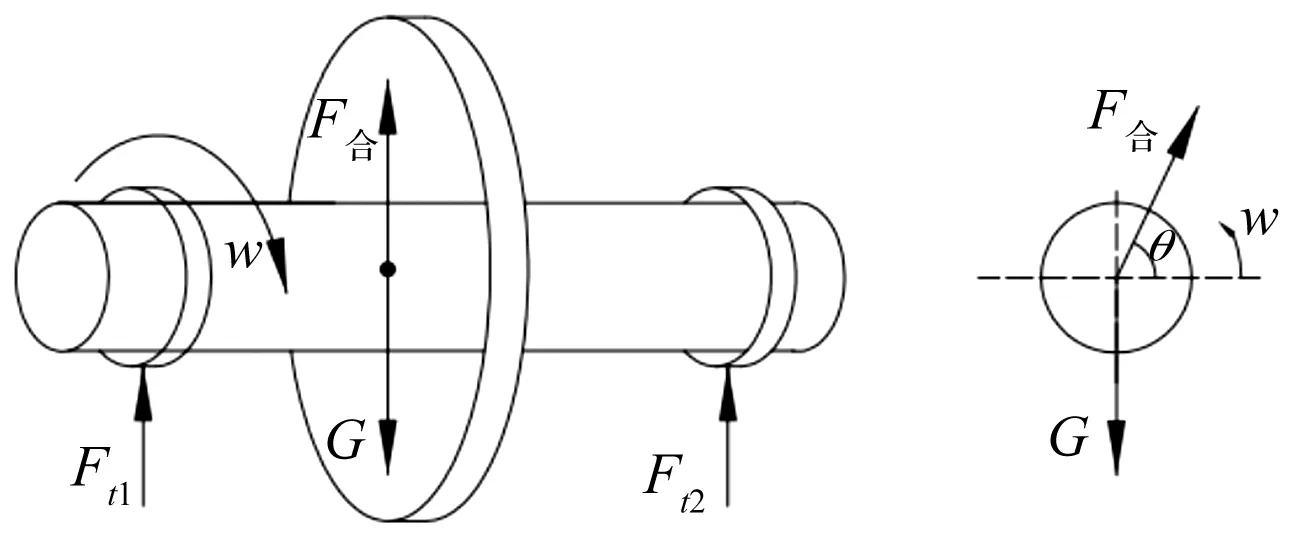
图5 转子受力分析Fig.5 Analysis of force acted on the rotor

那么对力进行正交分解：

(4)

从表达式中可以看出，当出现旋转失速时，转子受到的是与失速团运动频率相等的激振力作用，并且其受力形式与转子不平衡相类似。

3 轴流压气机失速仿真

3.1 压气机失速仿真控制

根据某一转速下的流量-全压性能曲线，通过适当的减小流量，控制出口的背压，将轴流压气机从稳态工况向失速状态逼近。在接近失速点处采用非定常计算，通过控制迭代时间、流量和全压的关系，逐渐模拟出流体内部的失速过程。

本文是在转子转速3 000 r/min的状态下，从3.7 kPa的背压出发增至3.71 kPa，物理时长选取为0.05 s，步长选择为200，那么每步的全压增加0.1 Pa，仿真时长内转子转动2.5转，每一步的仿真控制精度为0.000 01，计算迭代次数为20，计算过程耗时约8.5 h。

3.2 压气机失速过程

轴流压气机失速过程可以分为失速区域的形成、扩展和传播三部分，从仿真结果中了解失速过程主要从相对速度的变化来查看。

3.2.1 失速区域的形成

在轴流压气机稳定运行时，流经压气机叶片间隙的气流稳定，气流相对速度比较稳定且呈现对称，出现失速时会有部分相对速度的变化，如图6所示。

从图6中可以看出，从55步到75步过程中，方框内的低速区域从叶顶逐渐扩展到与之相邻的叶栅，初步形成失速区域。

3.2.2 失速区域的扩展

在失速区域的形成到稳定失速区传播的过程中，失速区域首先会扩展到一定大小的失速区，然后发生失速区域的整体传播。失速区域的扩展如图7所示。

从图中可以看出，在第95步失速区域大概在4～5个叶片区域，但到第125步，失速区域扩展到了6个叶栅左右。在失速区域扩展的同时，从失速区域起始位置可以看到轻微的失速区域传播。

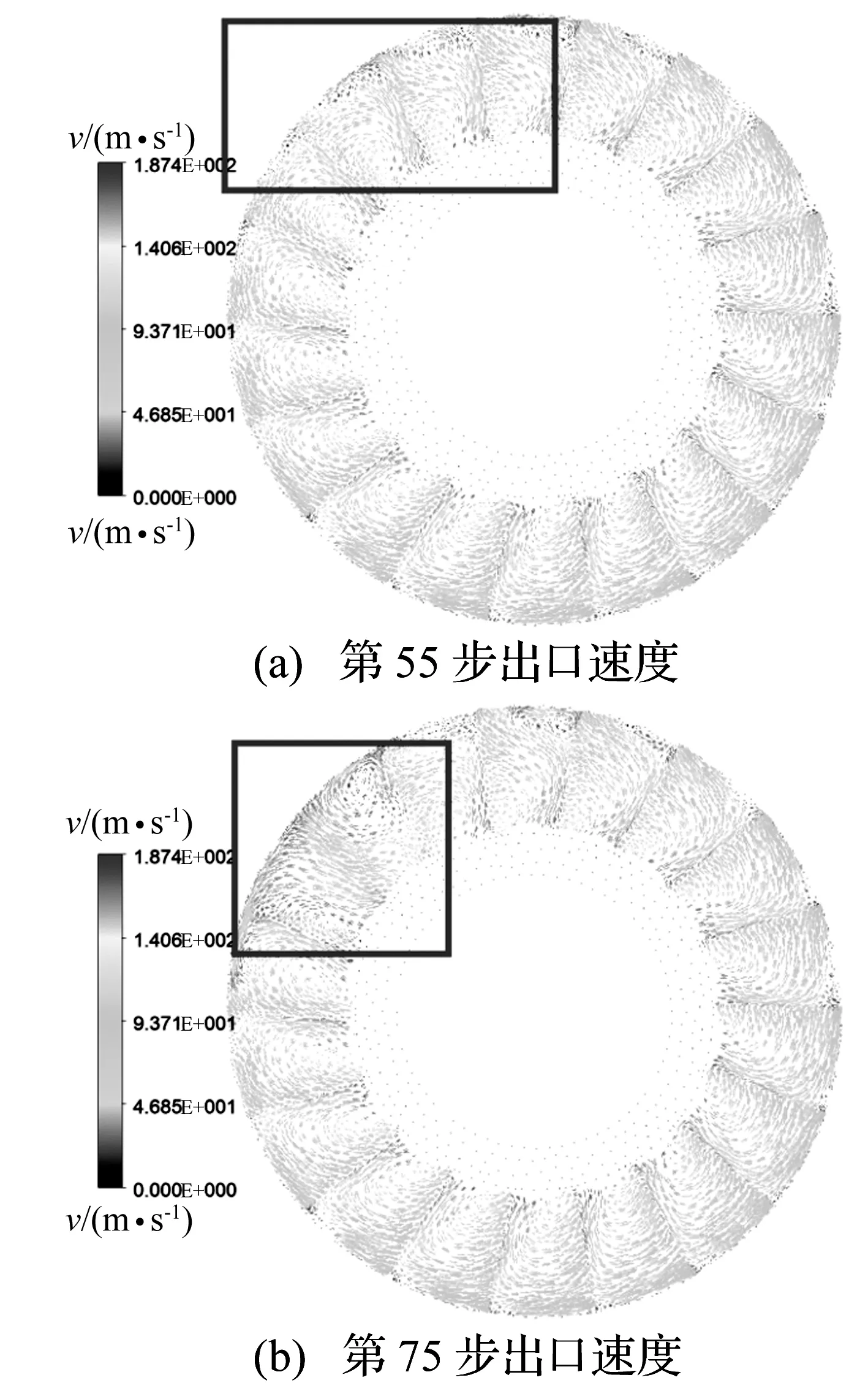
图6 失速区域形成Fig.6 The fomulation of rotating stall area

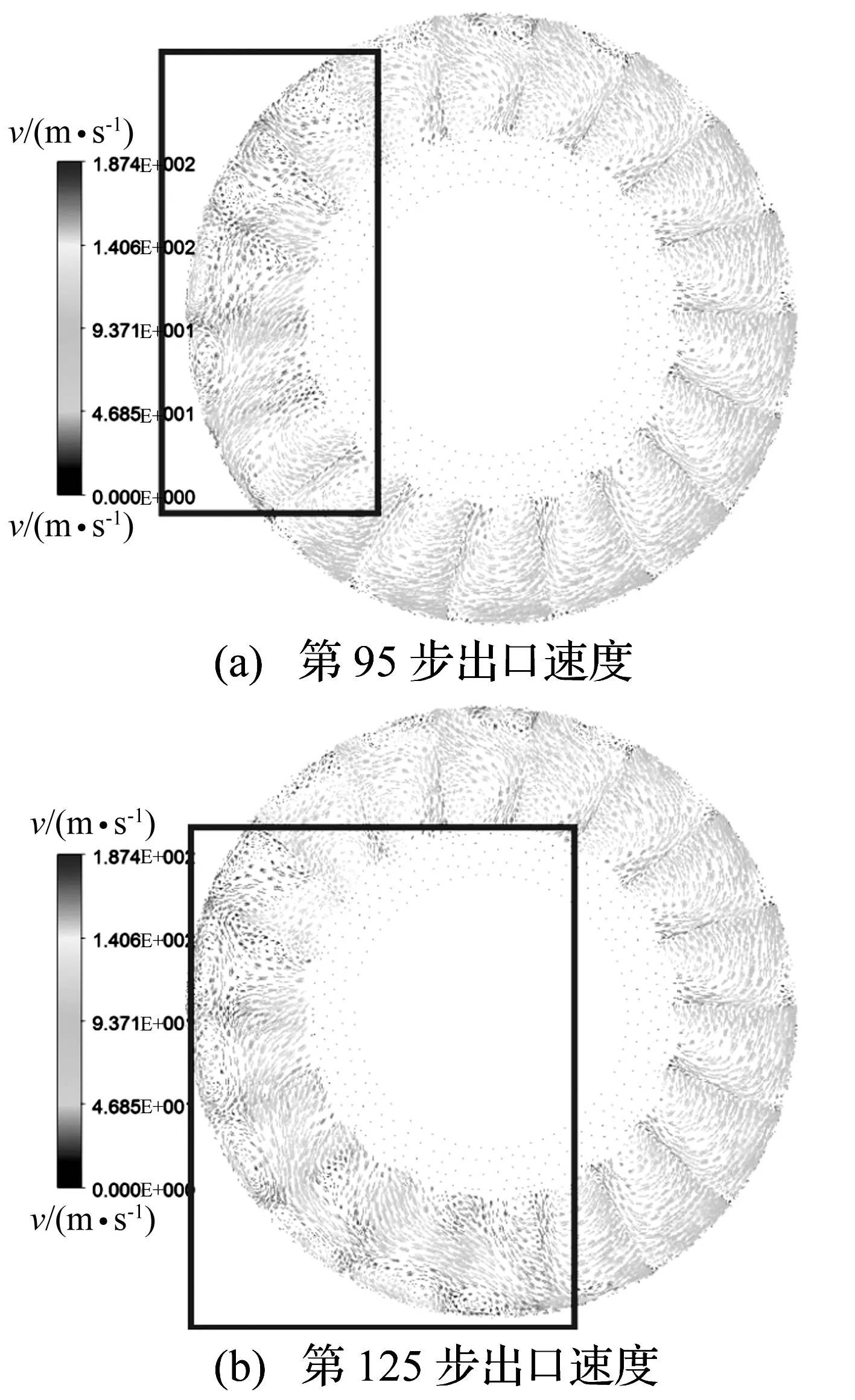
图7 失速区域的扩展Fig.7 The extension of rotating stall area

3.2.3 失速区域的传播

失速区域比较稳定之后，该失速区域会以一定的转速旋转，失速区域的传播如图8所示。

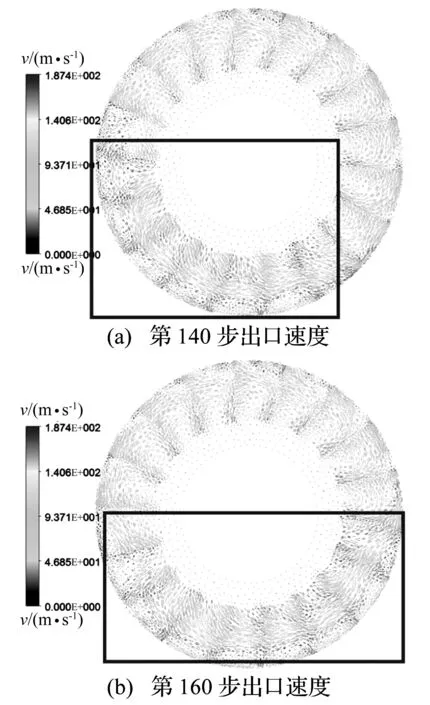
图8 失速区域的传播Fig.8 The spread of rotating stall area

从图8的20步迭代中可以看到，失速区域在6～7个叶栅左右，失速区域向前传播了将近2个叶栅的距离。20步对应的时长t：

t=T/N×20=0.05/200×20=1/200 (s)

(5)

式中:T为迭代物理总时长，N为迭代步数。20步内失速区域传播的角度θ：

θ=ψ/K×n=2π/18×2=2π/9 (rad)

(6)

式中,K为叶片数，ψ为K叶片对应的角度，n为失速传播的叶片数。那么失速传播角速度为：

ω′=θ/t=400/9π (rad/s)

(7)

那么相对转频为：

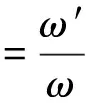
(8)

在流量全压变化情况下引发的失速，其传播速度为400π/9即为22.2 Hz左右，相对转频的转速比为0.44。

3.3 压气机失速速度变化

为分析失速过程中速度的变化，将迭代时间扩大了1 s，并选取了三个监测点A、C和E，布置如图9(a)所示，在完全失速时监控点A的速度分布如图9(b)。

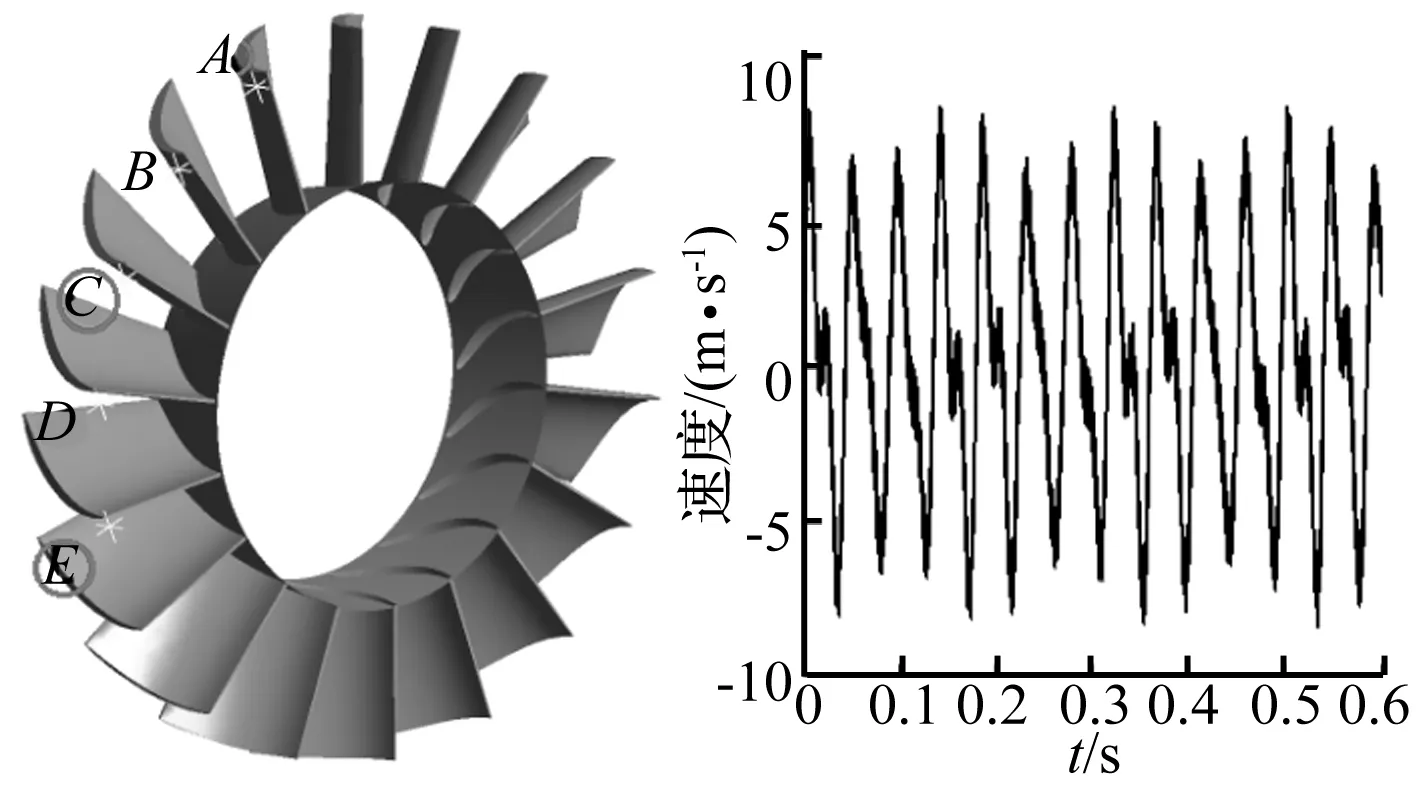
(a) 监测点 (b) A点速度图9 监测点位置及速度Fig.9 The locations and speeds of monitoring points

从监测点的速度分布图中可以看出，监测点的速度值在完全失速时呈现规律性的波动。为了获得速度的频率成分、揭示速度变化规律，将A点的速度进行频谱分析，如图10。

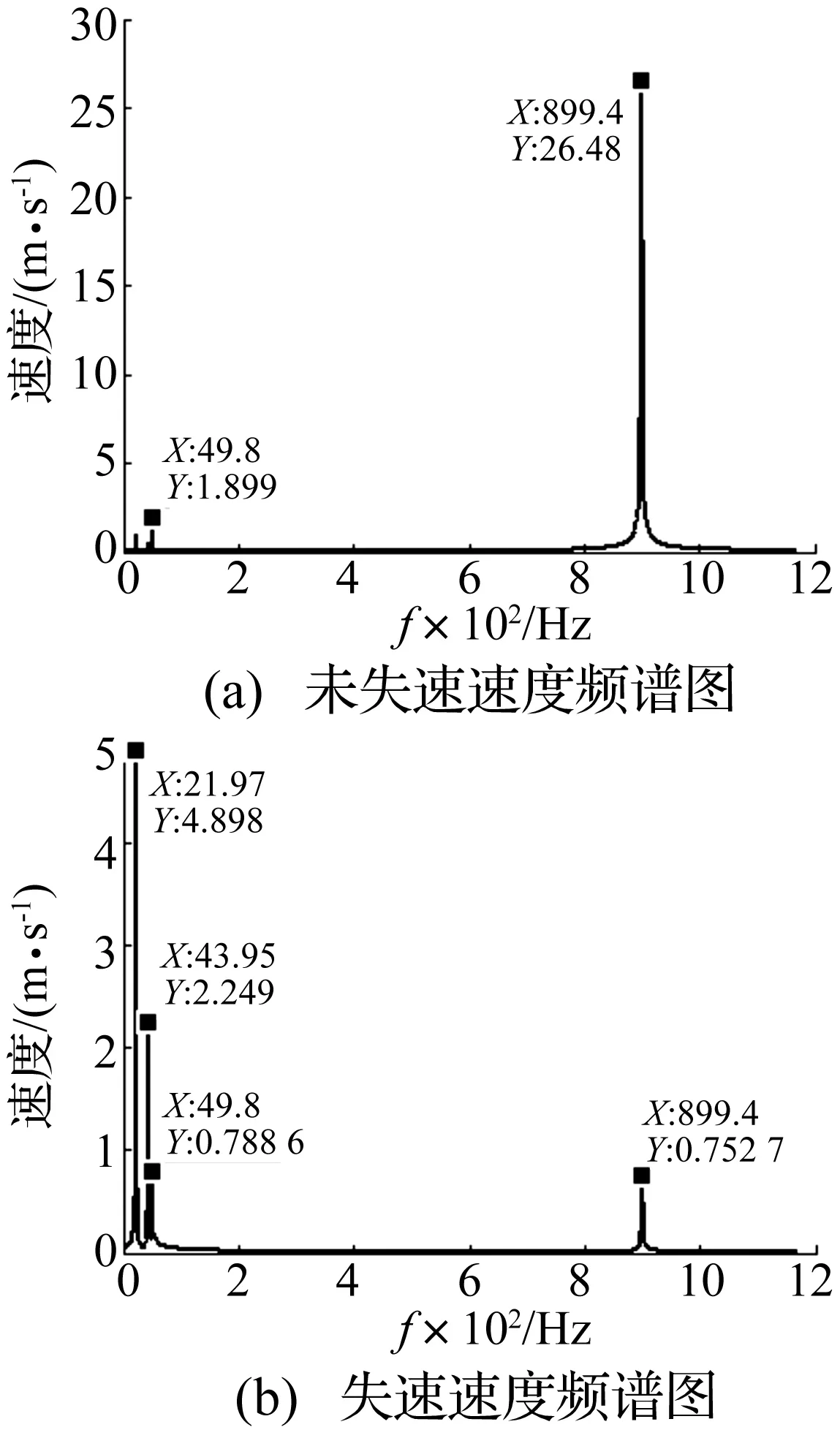
图10 失速前后A点速度频谱图Fig.10 Speed spectrum of point A in different conditions

从频谱中可以看出，在没有发生失速的情况下，A点速度频谱图中呈现的是899.4 Hz的频率，其余频率点表现幅值不明显，900 Hz频率为叶片的通过频率；在完全失速的情况下，A点速度频谱图中存在频率分别为21.97、43.95和899.4 Hz的三个频率特征，分别表示失速频率、失速频率的二倍频和叶片通过频率。

频谱分析得到的失速频率为21.97 Hz，在失速传播小节根据失速团的移动得到的失速角频率为22.2 Hz，两者分析结果一致。

3.4 压气机失速切向力变化

切向力是提供转矩的重要参数，当出现失速时，切向力骤变必然会导致转矩的变小，而转矩是压气机对流体做功的重要性能指标。在失速过程中，压气机叶片受力分为从稳态运行到失速切向力骤变和完全失速切向力稳定变化两个阶段。

(1)稳态运行到失速

轴流压气机的仿真从稳态运行到发生失速的过程中，切向力的变化如图11所示。

从图中可以看出，叶片1和叶片2在不同的时刻发生了阶梯性的骤降，叶片1切向力发生突增和骤减的时间分别为0.130 5 s和0.136 6 s，叶片2切向力发生突增和骤减的时间分别为0.152 2 s和0.160 4 s，同时根据两个叶片所处在的位置，从叶片1的失速发展到其对面叶片2的耗时0.021 7 s和0.023 8 s，取平均值为0.022 7 s，那么失速运动传播整周需要的时间为0.045 4 s，那么失速传播的频率约为22.03 Hz，与上述计算失速频率相符合。

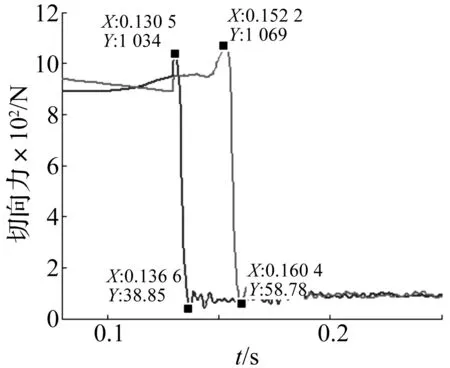
图11 失速起始阶段切向力Fig.11 Tangential forces in initial stage

(2) 完全失速状态

当轴流压气机发生完全失速时，叶片受到的切向力随时间呈现规律性的波动，如图12所示。

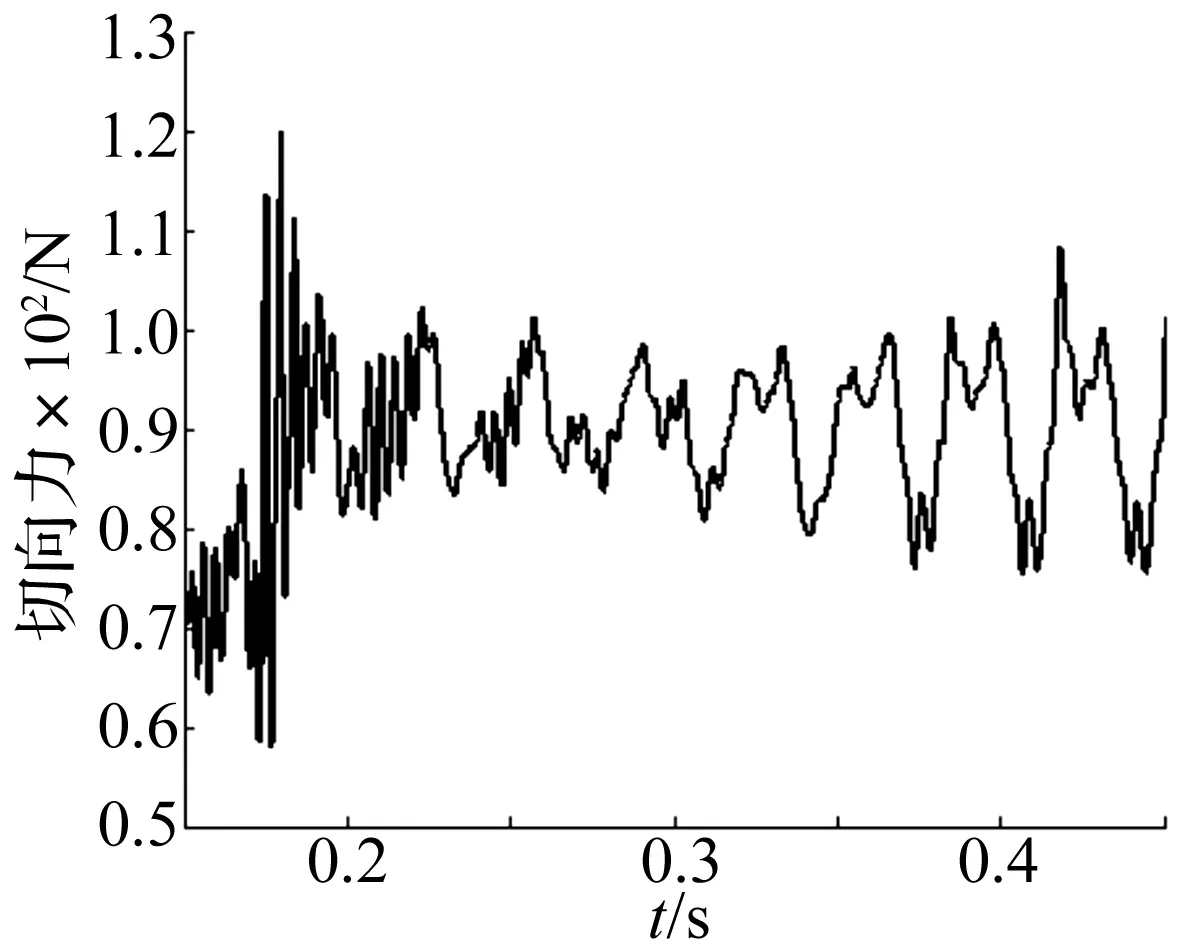
图12 完全失速阶段切向力Fig.12 Tangential forces in stall condition

可以看出，在轴流压气机发生完全失速时，随着失速区域的传播叶片所受切向力呈现一定的规律性，周期约为0.033 s左右，转换为频率大约在30 Hz附近，与失速传播频率有一定的差距。

4 结 论

本文从轴流压气机的工作过程和参数出发，通过轴流压气机失速原理的阐述进而对失速的引发条件进行了分类，并通过理论和仿真分析了失速作用下轴流压气机的失速传播及受力特性：

(1)压气机失速起源于内部流体对叶片的脱离，伴随着流道的堵塞和气流冲角的变化，失速区域会以一定较低的旋转速度进行传播；

(2)当轴流压气机发生旋转失速时，由于部分切向力的变化会引发压气机转子切向力的不平衡，进而导致转子受到与失速区域传播等频率的周期性径向激振力作用；

(3)轴流压气机的失速包括失速区域的形成、扩展和传播过程，同时失速区域的传播速度比转子转频低；

(4)在轴流压气机发生失速时，其转子叶片受到的切向力会因出口速度变化而发生骤减，之后以一定的频率发生较小幅值的变化。

[1] 蒋洪德，任静，李雪英. 重型燃气轮机现状与发展趋势[J]. 中国电机工程学报,2014,34(29):5096-5102. JIANG Hongde, REN Jing, LI Xueying. Status and development trend of the heavy duty gas turbine [J]. Proceedings of the CSEE, 2014,34(29):5096-5102.

[2] EPSTEIN A, FFOWCS J, GREITZER E. Active suppression of compressor instabilities [J]. Journal of Propulsion and Power, 1989,5: 204-211.

[3] DAY I J. Stall inception in axial flow compressor[J]. ASME Jouranl of Turbomachinery,1991, 115: 1-9.

[4] GREITZER E M. Surge and rotating stall in axial flow compressor—I:theoretical compression system model[J]. Journal of Engineering for Power, Transactions ASME,1976, 98:190-198.

[5] MOORE F K, GREITZER E M.Theory of POST—Stall transients in axial compression systems [J]. Journal of Engineering for Gas Turbines and Power,1986,108(2):231-239.

[6] FEULNER M R, HENDRICKS G J, PADUANO J D. Modeling for control of rotating stall in high speed multi-stage axial compressors[R]. ASME Paper 1994-GT-2, 1994.

[7] GRAVDAHL J T, EGELAND O. A Moorre-Greitzer axial compressor model with spool dynamics[C]// Proceeding of the 36th IEEE Conference on Decision and Control. San Diego, CA: IEEE, 1997:4714-4719.

[8] HU J, FOTTNER L. A new simplified model of post stall transients in axial compression system [J]. Journal of Thermal Science, 1999, 8(3): 176-189.

[9] 蒋康涛,徐刚，黄伟光，等.低速轴流压气机旋转失速的二维数值模拟[J]. 工程热物理学报,2003, 24(6): 935-938. JIANG Kangtao, XU Gang, HUANG Weiguang, et al. Two dimensional numerical simulation of rotating stall in a low speed axial compressor[J]. Journal of the Engineering Thermophysics, 2003, 24(6): 935-938.

[10] 蒋康涛, 张宏武，黄伟光，等.低速轴流压气机单转子旋转失速三维数值模拟和实验比较[J]. 工程热物理学报,2005, 26(增刊1): 77-80. JIANG Kangtao, ZHANG Hongwu,HUANG Weiguang,et al. Comparison of numerical simulation and experiment of rotating stall in a low speed axial compressor[J]. Journal of the Engineering Thermophysics, 2005, 26(Sup1): 77-80.

[11] 吴艳辉, 吴俊峰, 根仿玉. 轴流压气机转子近叶尖流动的试验和数值研究之一：准定常工况流动特征分析[J]. 工程热物理学报, 2013,34(5):836-840. WU Yanhui, WU Junfeng, GEN Fangyu. Experimental and numerical investigation of near-tip flow-field in an axial flow compressor rotor—part I: flow characteristics at quasi-steady operating conditions [J]. Journal of Engineering Thermophysics, 2013,34(5):836-840.

[12] 吴艳辉, 吴俊峰, 根仿玉. 轴流压气机转子近叶尖流动的试验和数值研究之二：近失速工况流动特征分析[J]. 工程热物理学报, 2014,35(1):60-65. WU Yanhui, WU Junfeng, GEN Fangyu. Experimental and numerical investigation of near-tip flow-field in an axial flow compressor rotor—part II: flow characteristics at near stall operating conditions [J]. Journal of Engineering Thermophysics, 2014,35(1):60-65.

Characteristics of forces acted on an axial flow compressor rotor under rotating stall condition

WAN Shuting1, DOU Longjiang1, ZHAN Changgeng2

(1. Department of Mechanical Engineering, North China Electric Power University, Baoding 071003, China;2. Hangzhou Steam Turbine Co., Ltd., Hangzhou 310000, China)

The velocity change and tangential force acted on the rotor of an axial flow compressor were analyzed in consideration of the rotating stall condition and the characteristics of tangential force. The principle and process of rotating stall were expounded theoretically. Then the tangential force acted on the rotor of axial flow compressor was deduced, when the compressor works in both normal and stall conditions. The characteristics of tangential force in rotating stall condition were obtained, and a comparison between the simulated and theoretical results was carried out. The feasibility of the theoretical analysis was verified by experimental simulations and the characteristics of tangential force and velocity change in rotating stall condition were obtained. The work mentioned above provides a useful reference to the subsequent vibration analysis and optimum structure design of compressor rotors.

rotating stall condition; axial flow compressor; rotor; characteristics of force

河北省自然科学基金(E201502008)

2015-12-01 修改稿收到日期：2016-01-12

万书亭 男，博士，教授,博士生导师，1970年生

豆龙江 男，博士，1988年生

TH453

A

10.13465/j.cnki.jvs.2017.02.016