测量单位观念的内涵及其教育价值
孙建
笔者有一次听《分米的认识》一课,课毕,表示1分米有多长时,几个举手表示的学生,双手张开,比肩要宽。当老师追问1分米等于几厘米时,学生们齐声回答10厘米。然而,他们并没有据此调整两手间距离的意识,足见缺少空间表象支撑的进率显苍白。由此可见,对测量单位、图形测量的认识和教学需要深入研究。
测量单位观念的内涵
测量即计量,指把一个量与一个作为标准的同类量进行比较的过程。其中作为标准的同类量即测量单位,表示测量标准的大小,是刻画图形大小的核心要素。图形测量是一种操作过程,在操作过程中教学测量单位重心在于概念与方法的生成、经验与思想的积淀,从而形成良好的单位观念。本研究提出的测量单位观念,具体内涵包括三个方面,以下逐一具体说明。
理解统一测量单位的必要性、形成测量单位表象,逐步建立主单位守恒。比较为测量提供了经验和基础,也提出了现实需求:统一测量单位。测量使不同位置上物体的间接比较便捷了,统一测量单位又使间接比较与交流变得通畅。国产客机C919的上百万个零部件由全球200多家企业提供,统一的测量单位至关重要。测量单位是以测量单位表象为基础的。测量单位表象也就是长度单位、面积单位、体积单位的标准图形在人脑中再现所形成的形状及大小。形成测量单位表象,才能准确把握数量。测量单位表象的形成表现为三个层面:一是根据单位名称能联想到相近的替代物,例如由1立方厘米,能想到一节手指或一粒樱桃的样子和大小;二是根据单位名称能联想到几何模型,例如由1平方分米,能在头脑中想象出或在纸上画出1分米乘1分米的正方形;三是面对实物或图形时能联想到适当的单位图形去划分。守恒的建立与发展是儿童测量能力发展的重要因素,主单位守恒是单位建立的重要方面。
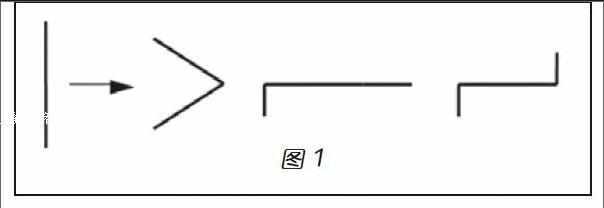
儿童关于长度、面积、体积的守恒存在较大差异。皮亚杰和英海尔德研究认为儿童在7.5至12岁已具有长度守恒的观念,儿童这时能够用任意长的物体作为普通的测量工具;儿童获得了测量时被分成的各部分长度守恒的概念。也就是二、三年级学生能够使用非标准或标准单位测量物体的长度,物体的位置变化时他们能做出长度不变的判断。并且,他们能对较长物体分段测量。(如图1)用左面的这根铁丝分别折成了右面不同的样子。二年级81.5%的学生认定它们同样长,但是能说明“同一个铁丝无论怎样折,长度不变”的学生只有30.3%;三年级91.1%的学生认定同样长,78.9%的学生能从长度守恒角度做出判断。这说明8至8.5岁儿童已基本建立起长度守恒,因此真正有意义的测量是从三年级学生开始的。
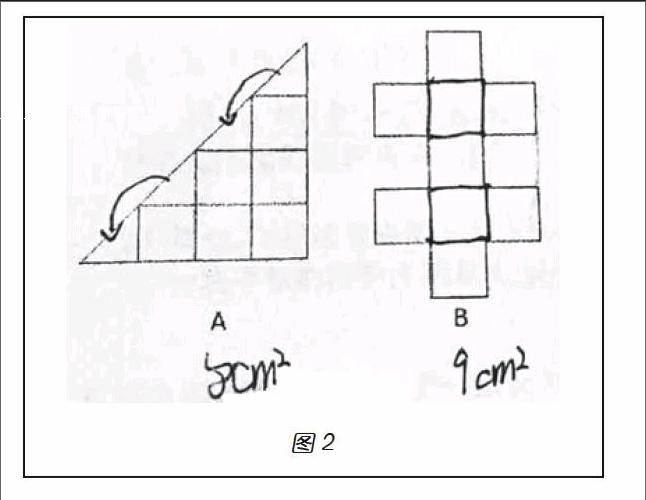
关于面积的守恒性,皮亚杰研究认为“(儿童)面积守恒性出现的时间与长度守恒性相同”,达到的水平表现为两个层面:一个层面是“利用叠置的方法”,用“若干个较小的图形分别正好符合或覆盖两个图形,那么这两个图形的面积必定相等。”也就是用标准或非标准面积单位密铺被测量的图形,从而比较它们的大小;另一个层面是“利用单位进行测量”,也就是比照给定的测量单位(形状、大小),在被测图形上划分、标记,然后数出个数来。在这个层面上,学生甚至可以对给定的单位进行简单的再分,这是学生面积守恒性的良好表现。例如:在比较下面图2中A、B两部分面积的大小时,三年级79.7%学生把A中两个三角形拼合成一个小正方形,将B中连通区域用线条划分,从而数出小正方形,完成比较。由此可见,三年级学生能依据“图中小正方形边长相等”推断出“每个小正方形面积相等”,即确定了面积单位,并能依据面积单位的空间形象对图形进行划分。
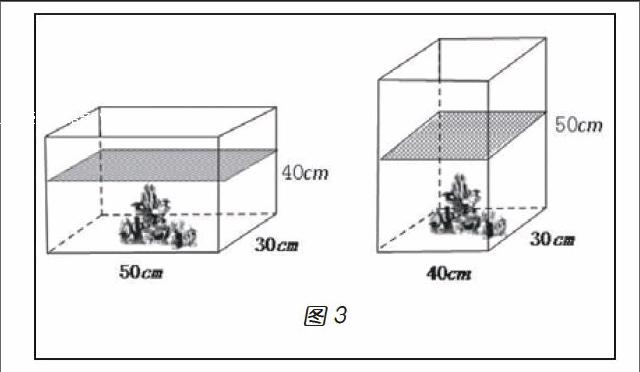
关于体积守恒,皮亚杰研究指出:儿童到12岁左右才能出现体积守恒概念。“儿童掌握了当外表的长度、宽度和高度改变时,内部体积或积木中所包含的‘房间空间是不变的这一观念。”即内部体积守恒这种类型。12岁以后,“这时儿童已能够根据三个维度的长度之间的关系来测量体积了。”即对内部体积的测量由数出体积单位个数上升到依据三个维度的长度与体积单位关系的智慧水平;“体积的守恒性也扩展到被占有的或被排开的水的体积的守恒。”即外部体积守恒,也就是内部空间与外部空间是守恒的,内部体积单位数与排开的外部的水、空气的体积相等。例如:将同样的假山石放入水箱中(如图3)。虽然水面上升的高度不同,但是78.3%的五年级学生能够根据假山石的体积不变推定排开的水的体积不变,他们初步理解了体积守恒。
提高学生测量水平
发展同维度下单位之间的联系,构建不同维度间测量单位之间的关系守恒,形成测量单位系统。测量单位间的联系包括:同一维度下测量单位间的进率和不同维度测量单位间的乘法结构的关系守恒。长度单位是守恒的,一方面表现为主单位(米)的长度守恒;另一方面表现为单位之间的关系守恒。长度单位间的进率选择十进制,使测量中的运算与数的运算一致,使测量结果的表示、单位换算十分简洁。面积单位、体积单位是长度单位在二维、三维空间量度的积,即乘法结构。因此,由长度单位间的十进制可以得到面积单位间百进制、体积单位间千进制关系。单位和进率构成测量单位系统。儿童大多是在相应守恒概念建立的初期甚至稍早时就开始学习长度、面积或体积测量。划分或复制等操作活动对不同年龄儿童、不同维度测量的影响程度如何?下面的调研可以反映出一些信息。
下面三组图形中,(2)号图形是(1)号图形的几倍?先填一填,再在图上画一画。并在空白处写出你的思考或你的发现。
由下表纵向观察,同年龄儿童划分一维、二维、三维图形的水平差异显著;横向观察,随儿童年龄的增长,划分面积、体积的能力明显提高,四年级达到峰值,五年级学生部分转化为运用计算测量图形的大小,因而划分的数据减少。由此可见,通过划分(或复制)是构建单位联系、形成单位系统、保持单位守恒的有效途径,并且利于促成守恒性上升到计算水平。
合理选择测量单位,正确测量或估测。在具体的问题情境中恰当地选择测量单位进行测量。在明确实际测量的对象后,选择恰当的测量单位决定着测量结果的准确程度和实用价值。比如,用平方厘米去估计一片树叶的面积就够用了,用它去逼近圆的面积,却难以感悟“两边夹”的数学原理;用立方分米(升)测量儿童每天的饮水量比较适度,用它统计家庭用水就过于繁琐。学生在亲身实践中不断积累正确使用工具测量、估测的经验,面对实际问题才能体会测量单位的现实意义,面对实际物体才能切实感受测量单位的大小,测量单位的表象、测量单位的联系和系统才能不断修正,进而达到守恒。
培养学生测量单位观念的价值
发展量化意识,突出“单位”思想 在测量单位观念建立的过程中,学生获得的经验和建立的观念,在其他量的研究中会发挥作用并使这种认识逐步发展到:任何量的量化,都必须有标准,而且标准必须统一。这使“单位”思想在量化中的核心地位得到普遍确立,从而在角度、货币、时间、重量等常见量的研究中主动寻找标准,探索创造单位,发展量化思维。建立测量单位表象的方法和经验也会促进学生借助实物或图形建立角度、时间、货币、重量单位表象或感知的实践与探索活动,逐步把感性认识上升为理性认识,形成量的抽象性与思维形象性的融合,单位思想不断深入,量的感觉不断发展。
培养联想类比,发展数学思维 在长度单位系统的构建过程中,应用某一单位沿直线方向复制或再分,产生新单位并形成相邻单位间的进率。学习面积单位时,依据面积单位与长度单位之间的关系,用面积单位向平面内两个维度扩展或再分;学习体积单位时,用体积单位向空间内三个方向堆积或再分,产生新单位,推导相邻单位间的进率。在这样的过程中,由长度单位系统中获得的经验联想到面积、体积单位系统的构建中,这种思维方法就是类比。类比方法在货币、时间以及重量等量的学习中还将发挥作用并得到进一步发展,进而促进数学思维的发展。
促进空间观念的发展 用实物、模型或图形建立单位表象;用长度单位复制、面积单位密铺、体积单位堆积等活动建立单位系统并在估测、测量实践活动中,图形测量的单位观念得到不断培养和发展。同时,良好的测量单位观念可以促进空间观念的发展。这主要体现在以下几方面:一是对图形测量的能力得到提高;二是由实物或模型抽象出几何图形的形状更具相似性、图形的结构特征更清晰;三是对图形的位置、图形的运动的刻画更准确;四是根据几何图形想象出所描述的实际物体匹配性更强;五是由语言描述产生联想画出的图形更接近原型。
参考文献
[1]裘光明.数学辞海:第一卷[M].太原:山西教育出版社,2002
[2](美)R·W·柯普兰.儿童怎样学习数学[M].李其维,康清鏕译.上海:上海教育出版社,1985:289,283,321,328.
[3]孙昌识,姚平子.儿童数学认知结构的发展与教育[M].北京:人民教育出版社,2005
(作者单位:北京教育学院丰台分院)

