具有双线性传染率的捕食-食饵种群传染病模型分析
杨 秀 香
(渭南师范学院 数理学院,陕西 渭南 714099)
【自然科学基础理论研究】
具有双线性传染率的捕食-食饵种群传染病模型分析
杨 秀 香
(渭南师范学院 数理学院,陕西 渭南 714099)
利用种群动力学理论及传染病模型理论,研究了一类具有双线性传染率的捕食-食饵传染病模型的全局稳定性,考虑种群内部竞争影响和染病捕食者的捕获率和自然死亡率等因素,得到了无病平衡点和地方病平衡点存在的阈值R0的范围,并借助于李雅普诺夫函数的构造,证明了无病平衡点和地方病平衡点的全局稳定性。
捕食-食饵模型;平衡点;阈值;李雅普诺夫函数;全局稳定性
0 引言
在科技飞速发展、自然变异和人类不合理活动的影响下,地球上的种群都在面临着减少甚至灭绝的危险,在种群的世界里除了自然灾害、环境污染等外,还有什么影响着它们的变化呢?生存环境匮乏、种群之间竞争、人工扑杀、传染病影响等,表现得更为突出。因此,生态流行病模型的研究已成为生物数学研究的热点,将种群动力学与传染病动力学模型有机结合起来,可更为实际地研究种群的变化规律。然而世间万物的联系是错综复杂的,种群之间也不例外,这其中不仅有疾病传播的因素、捕食与被捕食的食物链因素,还有同种群内部的竞争因素等,都在影响着种群的变化。文献[1-6]考虑到种群的内部竞争,讨论食饵、捕食者有密度制约,染病捕食者不能捕食但无永久免疫力、传染率均为双线性的生态流行病SIS模型,文献[7-8]研究了单种群的传染病模型。在此基础上,依据微分方程的稳定性、种群动力学及传染病模型理论知识[9-10],本文考虑染病类捕食者也具有一定的捕食能力,捕食者只有食饵供给能量,且捕食者之间的流行病传染率为双线性函数,建立符合生态意义的数学模型:
(1)
其中:X(t)为t时刻食饵的数量;K为食饵的环境容纳量;S(t)为t时刻捕食者易感类的数量;I(t)为t时刻染病捕食者的数量;α为食饵种群的内禀增长率;β为捕食者的接触率;p,q分别为捕食者中易感者的捕获率与染病者的捕食率,染病捕食者不具有捕获能力;d1、d2分别为易感捕食者、染病捕食者的死亡率,包括自然死亡率和因病死亡率,d1 定义1[9]对于方程组 (2) 引理1[9](赫尔维兹(Hurwitz)判别代数方程的根均具有负实部)设给定常系数的n次代数方程 a0λn+a1λn-1+a2λn-2+…+an-1λ+an=0, (3) Δ1=a1>0,Δ2>0,Δ3>0,…,Δn-1>0,an>0。 引理2[10]若一阶常系数线性微分方程组(2)的特征方程det(A-λE)=0的根均具有负实部,则方程组的任一解当t→0时都趋于0,从而系统的平衡点是渐近稳定的;若特征值的实部为零的根是单根,则方程的任一解有界,系统的平衡点是稳定的,但不一定渐近稳定。 所以系统(1)满足初始条件(X0,S0,I0)∈R3的正解最终有界。 (4) 特征方程 det(J(E)-λE)=0。 (5) (1)对于平衡点E0=(0,0,0),特征方程有一正两负特征根,λ10=α,λ20=-d1,λ30=-(d2+δ),因此平衡点E0=(0,0,0)不稳定。 (2)对于平衡点E1=(K,0,0),特征根λ11=-α,λ21=pK-d1,λ31=qK-(d2+δ),当pK-d1<0,qK 对应的特征方程为: 即 λ3+A1λ2+A2λ+A3=0。 A1A2-A3=μω2-(μ2+p2S*I*+pqX*S*+νβI*)ω+μq2X*I*+μp2S*X*>0。 由引理1、引理2可得系统(1)的唯一正平衡点E3=(X*,S*,I*)是局部渐近稳定的。 定理4 当R0>1,pK-d1>0,qK 证明 正平衡点E3=(X*,S*,I*)是局部渐近稳定的。 构造正定的Lyapunov函数 (5) 由引理3可得,系统(1)的正平衡点E*=(X*,S*,I*)是全局渐近稳定的。 αβqX*2+Kq(pd2-αβ-qd1)X*+K[αβd2+(d2+δ)(qd1-pd2)]=0, 捕食者中疾病最终形成地方病。 [1] 韩俊杰,窦霁红,李涛.一类带连续性捕杀效应的生态-流行病SIS模型[J].西北大学学报(自然科学版),2013,43(3):345-350. [2] 王娟,韩欲青,李学志.一类具有非线性发生率的传染病模型的稳定性[J].数学的实践与认识,2012,42(12):112-117. [3] 刘洪涛.一类捕食-传染病模型的稳定性分析[J].纺织高校基础科学学报,2012,25(1):59-60. [4] 张辉,徐文雄.一类潜伏期和染病期均传染SEIS模型的渐近定性分析[J].陕西师范大学学报(自然科学版),2008,36(6):5-9. [5] 马丽娜,刘烁,李建全,等.一类具有垂直传播的SIS捕食传染病模型的全局分析[J].西北大学学报(自然科学版),2011,41(4):582-588. [6] 杨亚莉,李建全,赵伟.一类捕食者存在疾病的捕食系统传染病模型[J].数学的实践与认识,2009,39(17):104-107. [7] Yang Xiuxiang,Xue Chunrong.An SIQS infectious disease model with isolation[J].International Journal of Biomathematics,2008,(2):239-245. [8] Yang Xiuxiang,Cheng Yuanji.Global Dynamics SIQRS Quarantine Epidemic Models with Generalized Separable Incidence Rate[J].生物数学学报,2014,29(2):193-198. [9] 王高雄,周之铭,朱思铭,等.常微分方程[M].第5版.北京:高等教育出版社,2006:248-277. [10] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004. 【责任编辑 牛怀岗】 Analysis of Predator-prey of Epidemic Model with Double Linear Infection Rate YANG Xiu-xiang (School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China) This paper studies a predator-prey epidemic model with double linear infection rate. We have obtained a threshold value R0and shown that there is only a disease free equilibrium point when R0<1, and there is also an endemic equilibrium point if R0>1. With the help of Lyapunov function, we have shown that disease free and endemic equilibrium point is globally stable. predator-prey model; equilibrium point; threshold; Lyapunov function; global stability O175.13 A 1009-5128(2017)04-0005-06 2016-10-08 陕西省扶持学科数学学科基金资助项目:微分方程的稳定性理论及其在生物数学中的应用(14SXZD008);渭南师范学院科研计划项目:利用生态动力学模型研究秦东地区黄河湿地的资源保护与最优化分析(13YKF003);渭南师范学院教育科学研究项目:西方教师教育大学与中小学合作体制特点(2014JYKX021) 杨秀香(1966—),女,陕西富平人,渭南师范学院数理学院教授,主要从事生态数学及微分方程研究。1 定义与引理
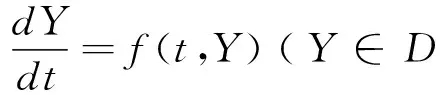
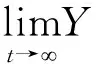
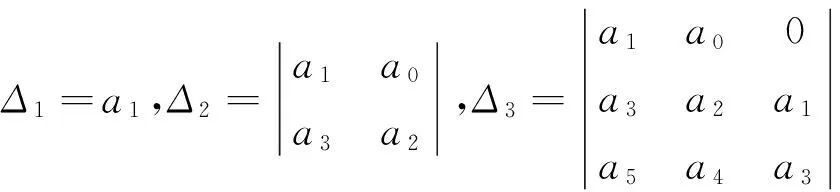
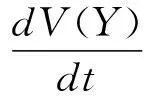
2 解的有界性
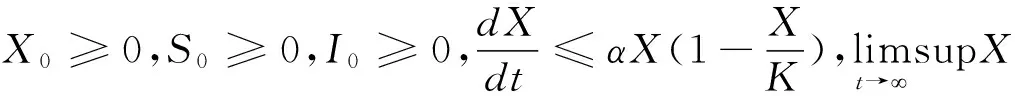
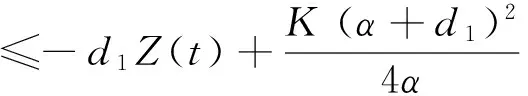
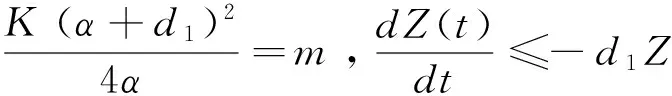
3 平衡点的存在性与局部渐近稳定性
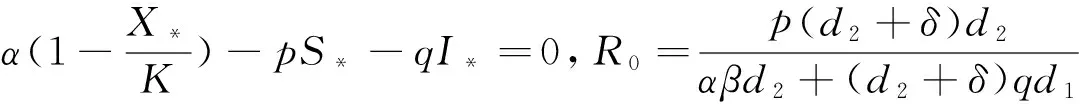
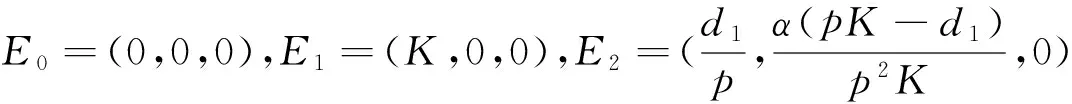
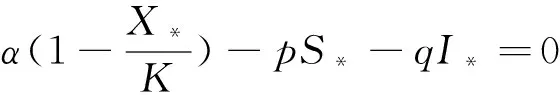
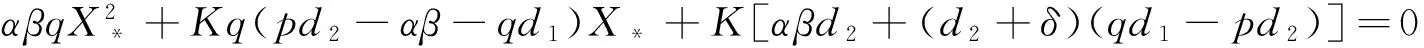
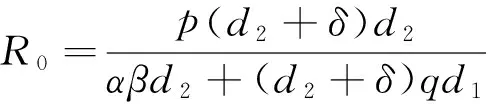
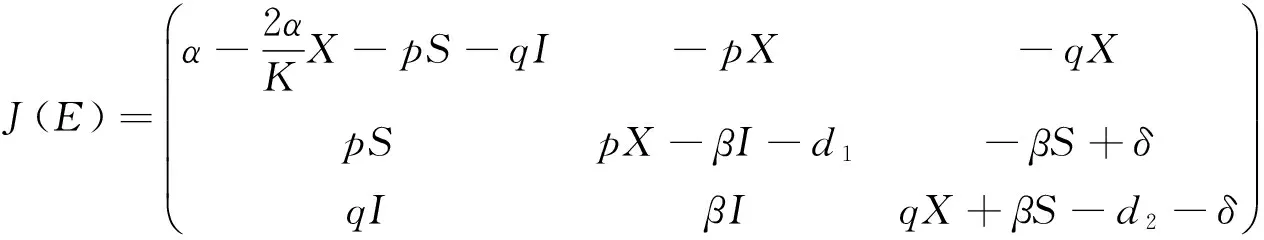
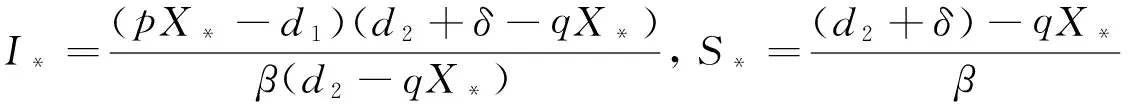
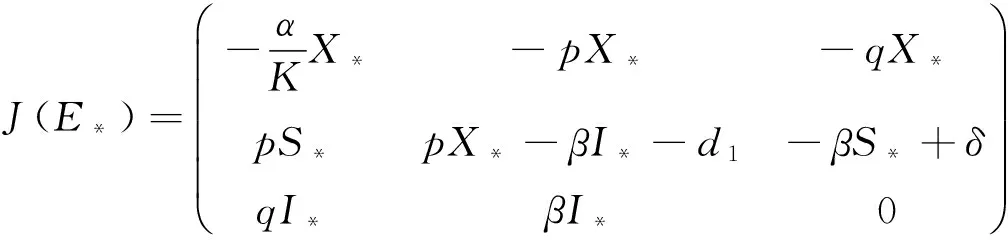
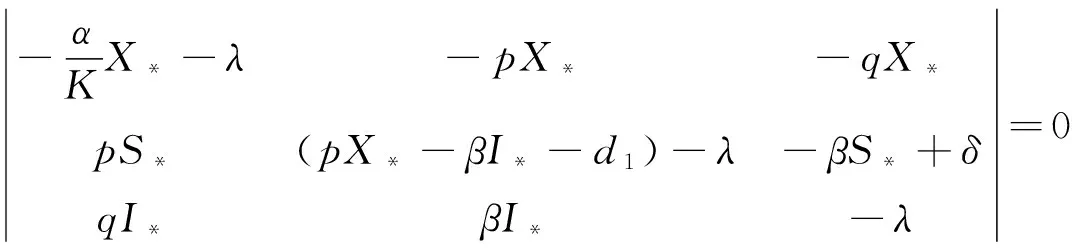
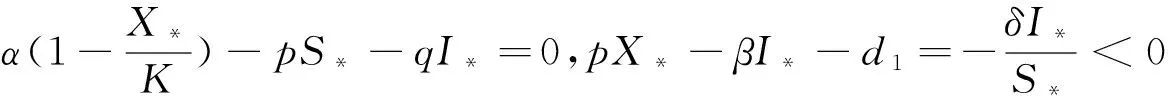
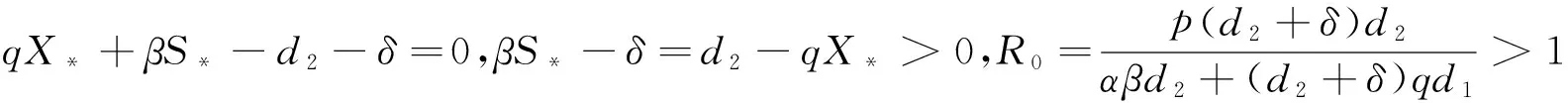
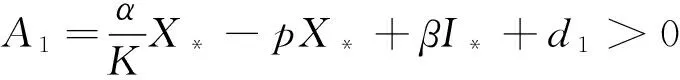

4 平衡点的全局渐近稳定性
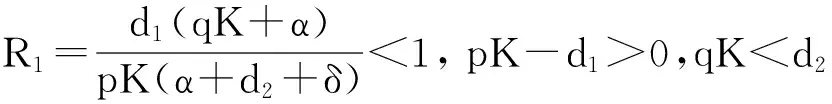
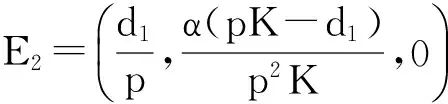
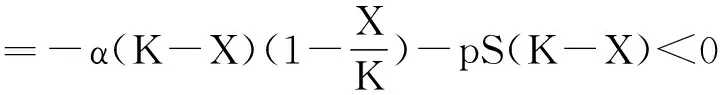
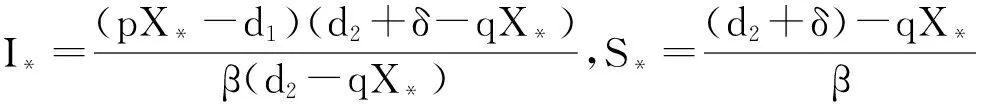
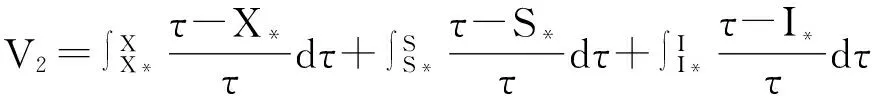
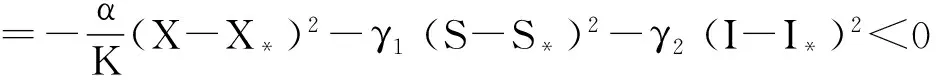
5 生物意义