浅谈流体力学流量特性的矛盾与统一
袁晓明+罗成+李明
摘要:流体力学是液压与气压传动的理论基础,液压与气压传动是流体力学的延伸和发展。在流体力学的学习和研究过程中,一直存在着表面上似乎相互矛盾的问题,即从连续性方程来看,当管道半径增大时,其过流断面面积同样增大,流体平均流速减小;然而根据节流口的节流特性,可通过改变节流口过流断面面积控制流经过流断面的流量。从表面上理解,连续性方程与节流方程的结论存在矛盾。在对二者物理意义进行理论分析的基础上,以数学公式的方式进行了推导计算,揭示了上述表面矛盾的本质,得出了两者并不矛盾,且可以相互统一的结论。
关键词:流体力学;连续性方程;节流口;节流特性
中图分类号:G642.41 文献标志码:A 文章编号:1674-9324(2017)03-0210-02
一、前言
在流体力学的学习和研究过程中,一直存在着表面上相互矛盾的问题,即从连续性方程来看,当管道半径r增大时,其过流断面面积A同样增大,流体平均流速v减小;当管道半径r减小时,其过流断面面积A同样减小,流体平均流速v增大。流量连续性方程的物理意义为流体流经不同过流断面的流量相同。然而根据节流口节流特性,可通过改变过流断面面积控制流经过流断面的流量。在以往的学习研究中几乎没有提出过此矛盾问题,因为连续性方程是普遍适用的物理规律,而节流口节流特性又是经过实验验证的正确结论。如何理这个矛盾,已经成为流体力学课程教学与研究中需要解决的一个关键问题。
二、从物理意义及适用条件进行分析
1.流体力学中连续性方程的物理意义。质量守恒方程是自然界的客观规律(不考虑原子核反应的质量互换等问题),流体力学也必须遵守这个规律。在流场中任取一个控制体积,可通过连续性数学方程,即流进与流出控制体积的流体质量与控制体积内流体质量的变化关系的方程,描述流体流动的质量守恒关系。若在某一时间间隔内,流进控制体积的流体质量大于流出的质量,则在控制体积内的流体质量必然增加,但由于体积是确定不变的,所以流体的密度必然要增大,反之则减小。如果流体为不可压缩流体,即流体的密度保持不变,则流进控制体积的流体质量必然等于流出的质量,这就是连续性方程的物理本质。
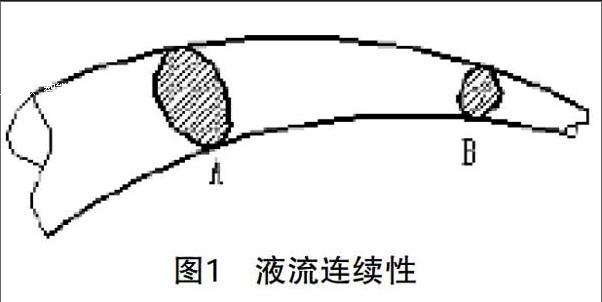
2.节流口节流特性的物理意义。流体流经细长孔、薄壁孔或狭缝等节流口时会遇到阻力,若改变它们的通流截面积或通流长度,则可调节通过节流口的流量,即节流口节流特性是使流体流经小孔或缝隙来调节其过流流量。不同节流口流量特性的通用表达式为Q=Av=KAΔpm。式中,A为孔口或缝隙的过流面积;Δp为孔口或缝隙的前后压差;K为节流系数,由节流口几何形状及流体性质等因素决定;m为节流口形状和结构决定的指数,当节流口近似为薄壁孔口时取0.5,当节流口近似为细长小孔时取1。流体经过节流口过流断面时会产生压差,当节流口面积不变时,压差保持不变,则流量不会改变(不考虑其他外负载影响)。当节流口面积改变后,其前后压差也改变,通过此节流口过流断面流量亦改变。这就是节流特性的物理本质。假设控制体积如图1所示,若流体为不可压缩流体,流体从过流断面A流入,从过流断面B流出,则通过过流断面积A和B的流量必然相同,即,当过流断面积变化时,流经各过流断面的流量保持不变。
从上述两个物理本质可以看出,连续性方程侧重于研究一个空间内同一时刻流经两个或多个不同过流断面的流量情况,而节流口节流特性方程侧重于研究不同时刻流体流经节流口过流断面的流量变化情况。两者研究的侧重点不同,因而会得出看似相矛盾的结论,即使如此两者也是可以进行统一的。
三、从数学模型进行推导,将连续性方程与节流特性表达出的物理规律进行统一
假设以圆形过流断面为研究对象。假设流体的体积流量Q是不变的。对于不可压缩流体的一维管道流动,从连续性方程可知,Q=Av=πr2v=const,当管道半径r增大时,则流速v与半径r的平方成反比例关系。从节流口的流量公式可知,Q=KAΔpm,流体流经节流口的阻力分为沿程阻力和局部阻力,式中m的取值与节流口形式有关,当节流口为细长孔时m为,当节流口为薄壁孔时m为0.5,这是由于口为细长孔时压差主要用于克服沿程阻力损失,而当节流口为薄壁孔时压差主要用于克服局部阻力损失。
1.节流孔为细长孔。流体流经细长孔时,一般为层流状态,所以细长孔的流量公式为
Q=πr4Δp/(8μL),若管长L取得足够小,则Δp/L可改写为dp/dL,其中dp/dL为沿管道轴线上的压力梯度。则细长孔流量公式可写为Q=πr4dp/(8μdL),当Q一定时,压力梯度dp/dL与半径r的4次方成反比例关系。且Q=Av=πr2v,则v=r2dp/(2μdL),即流速v与半径r的平方成反比例关系。因此,此结论与上述连续性方程的结论完全相同。
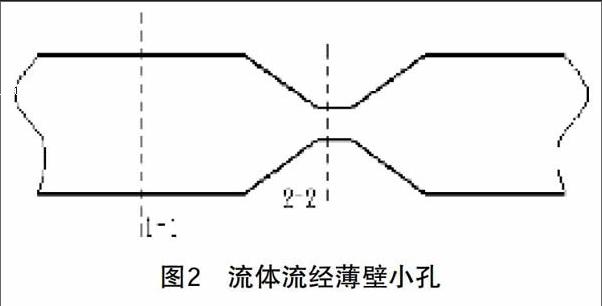
2.节流口为薄壁小孔。通过薄壁小孔的流量可以用伯努力方程求得。在管道处和小孔处各取过流断面1-1和过流断面2-2,如图2所示:
由伯努利方程可知,
p1/γ+v12/(2g)+h1=p2/γ+v22/(2g)+h2,式中,p1、v1、h1分别为过流断面1-1位置单位重力流体的压强势能、动能和重力势能;p2、v2、h2分别为过流断面2-2位置单位重力流体的压强势能、动能和重力势能;γ为重度;g为重力加速度。因为管道面积比小孔面积大得多,所以v1远大于v2,伯努利方程中的动能项v12/(2g)可忽略不计,假设h1=h2,则p1/γ=p2/γ+v22/(2g),流经薄壁小孔过流断面的流速v2=sqrt(2gΔp/γ),Δp为过流断面1-1和2-2之间的压差。流经小孔的流量为Q=Asqrt(2gΔp/γ)。其中小孔前后压差为局部压力损失,则Δp=ηγv2/(2g)。因此,流经薄壁小孔的流量即为Q=πr2vsqrt(η),式中,r为薄壁小孔过流断面的半径;v为薄壁小孔过流断面的平均流速;η为局部阻力系数。从上式可知,πsqrt(η)为常量,薄壁小孔过流断面的平均流速v与薄壁小孔过流断的面半径r的平方成反比。由此可知,此结论与上述连续性方程的结论完全相同。
四、结论
虽然上述分析以圆形孔道过流截面为研究对象,但其分析方法和结论对其他形式的过流断面,如椭圆形、矩形、方形、扁方形、等边三角形、直角三角形、圆形环状等,同样适用,读者可根据上述分析方法与思想对新的过流断面进行验证。通过上述讨论可知,流量连续性方程与节流口节流特性方程并不矛盾,二者是辩证统一的。书本中很多看似矛盾的问题,只要从理论本质出发进行分析,均能够对其进行正确的认识和理解。
参考文献:
[1]罗志骏.液压气动设计计算图表[M].第一版.机械工业出版社,1981.
[2]盛敬超.流体力学[M].第一版.机械工业出版社,1980.
[3]那日,晨阳.关于连续性方程和泊肃叶公式相互矛盾的理解[J].内蒙古医学院学报,1992,(6).
[4]西德,W.巴克.液压阻力系统学[M].机械工业出版社,1980.
Contradictionand Unity of the Continuity Equation and Throttling Characteristics
YUAN Xiao-ming1,2,LUO Cheng1,2,LI Ming3
(1.Hebei Key Laboratory of Heavy Mechinery Fluid Power Transimission and Control,Yanshan University,Qinhuangdao,Hebei 066004,China;2.Key Laboratory of Advanced Forging & Stamping Technology and Science (Yanshan University),Ministry of Education of China,Qinhuangdao,Hebei 066004,China;
3.Faculty of Science,Yanshan University,Qinhuangdao,Hebei 066004,China)
Abstract:Fluid mechanics is the theoretical basis for hydraulic transmission,in the learning process of the hydraulic fluid mechanics,there has been a problem to the surface to be contradictory,namely from the continuity equation,when the flow pipe radius increases,its closure area also increases,the fluid average flow velocity decreases.According to the properties of throttling mouth,however,by controlling the throttle mouth shut off to control the size of the area through the intercepting traffic below.Understand from the surface,and the equation of continuity of conclusion.In this paper,from both the physical significance of the nature has carried on the theoretical analysis and mathematical model was derived from both,it is concluded that the two are not contradictory,and can be unified.
Key words:fluid mechanics;continuity equation;the throttle opening;throttling characteristics

