一种基于板壳理论对芯片翘曲变形的研究

郭 威，王小龙，谢建友，张 锐

（华天科技（西安）有限公司，西安710018）

一种基于板壳理论对芯片翘曲变形的研究

郭 威，王小龙，谢建友，张 锐

（华天科技（西安）有限公司，西安710018）

在温度变化过程中，由于芯片封装层叠结构及材料热膨胀系数的不匹配，封装结构会发生翘曲现象。芯片翘曲关乎到电子元器件的可靠性及质量，准确快速地计算翘曲对于封装结构设计及材料选型有着重要意义。基于多层板翘曲理论，建立了一套对芯片翘曲进行计算的双曲率模型。以常规的指纹识别芯片为例，通过实验测量及有限元仿真的对比验证，证明了该理论可以满足工程计算精度。该模型可以拓展到其余多层板结构的翘曲计算，对于优化芯片翘曲设计有重要意义。

芯片翘曲；有限元仿真；双曲率

1 引言

封装层叠结构由于在温度变化过程中材料属性的不匹配，最终会导致结构翘曲的发生[1]，对产品后续的可靠性和服役寿命等有着重要影响。结构的翘曲会直接影响到封装结构的共面度[2]，引发芯片断裂[3]、芯片分层[4]和焊点失效，直接关系到质量。因此，准确快速地计算芯片封装结构的翘曲对于芯片封装质量及产品的可靠性有着重要的意义[5]。本文以常规指纹芯片封装结构为模型，结合实验、理论模型、有限元仿真3个方面来验证，基于板壳理论，建立计算芯片封装结构翘曲的公式。

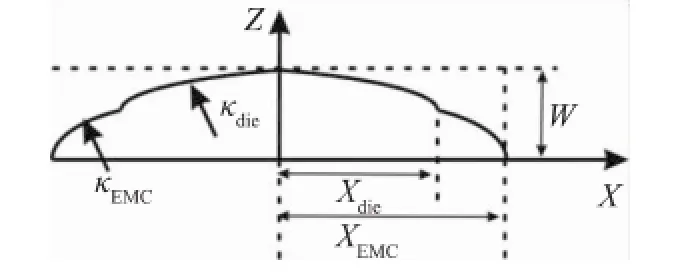
图1 芯片封装结构翘曲的双曲率模型

图1所示为芯片封装结构翘曲的双曲率模型，其中Xdie和XEMC分别是芯片和塑封料边界距离中心位置的距离，κdie和κEMC是芯片部分和塑封料部分的曲率，整个结构的翘曲变形w受这双曲率共同决定。

已有的一些翘曲计算公式基于芯片厚度较薄，将芯片层扩充外延形成层合板简化模型，或者近似地将芯片用塑封料取代形成多层板结构[6]。这些简化方法在芯片尺寸特别大或特别小且芯片厚度很薄的情况下才比较合理，但不适用于大多数的封装结构情况。也有理论采用复合材料的等效方法，将芯片层的芯片部分与塑封料按照体积比例进行等效，将芯片层赋予成等效材料参数，形成多层板模型[5,7]。但芯片和塑封料是各自独立的结构单元，这种简化也会存在误差。由于芯片的主要材料是硅，其杨氏模量相比塑封料高出4倍左右，最终芯片封装结构翘曲的曲率会在芯片和塑封料边界处发生阶跃，如图1所示，即最终翘曲会受上述两个曲率影响。本文基于双曲率模型，考虑芯片部分和塑封料的结构差异，对已有翘曲计算公式进行了修正，采用Shadow moire仪器对芯片样品进行实际测量，并使用ANSYS 17.0 workbench静力学模块进行有限元仿真，对新的修正模型进行验证。

2 多层板翘曲的理论模型

芯片的封装结构通常是由塑封料、芯片、基板等多层结构组成，设平面坐标系xoy，如图2所示。这种倒装芯片类型的结构可以被当成一个多层板。翘曲是由于多层板结构及材料的不匹配引起的。在温度载荷下，各层材料变形不一致，多层板间的应力是靠层间接触来传递的。基于经典的板壳理论，就可以去建立一套计算芯片封装结构翘曲的理论公式。

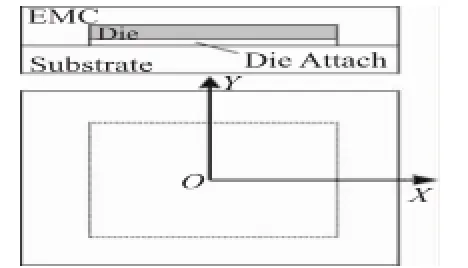
图2 芯片封装结构的简化模型

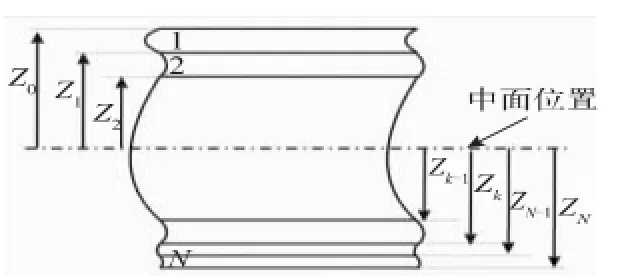
图3 简化的多层板结构模型

图3所示为简化的多层板结构模型，其中虚线是中面位置，Z0～ZN是以中面为基准，到各层板边界的距离。对于一个多层板的横截面来说，其结构可以简化为图3所示。多层板结构翘曲是由其平面应变和曲率决定的，并且需要满足变形协调方程，层间的应变才能匹配[5]。当对层合板结构施加温度载荷(ΔT)时，对于第k层板，其应力-应变的关系可以表示为[8]：

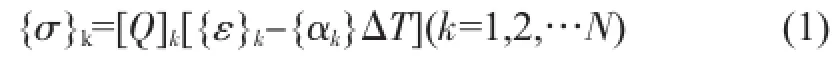
其中，σ、ε是应力与应变，α是热膨胀系数，对于各向同性材料，刚度矩阵[Q]k可以表示为：

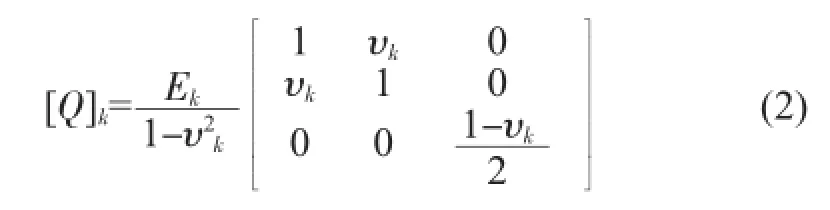
根据板壳理论[8]，板壳中面的平面应变、曲率与结构所受的力、力矩的关系如下：

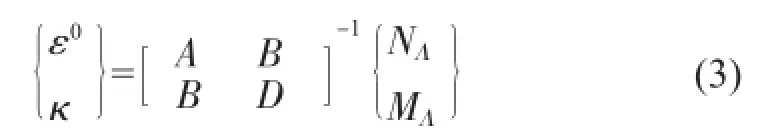
其中层合板的内力矩阵{NΛ}和{MΛ}为：

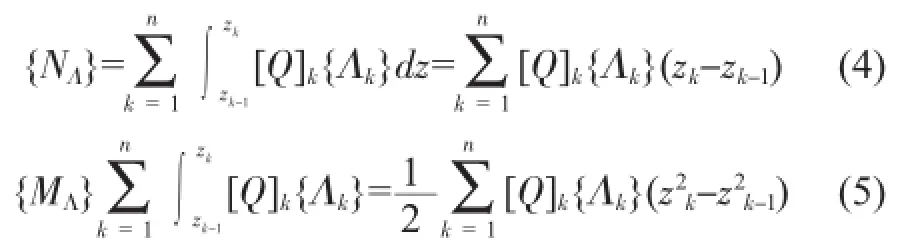
温度引起的变形量{Λk}为：

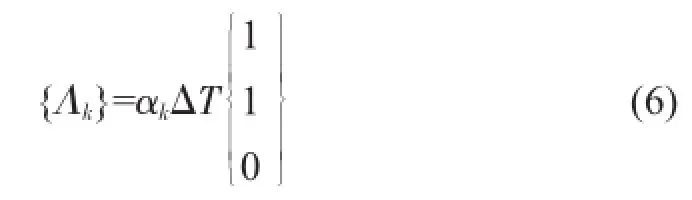
多层板结构的刚度矩阵A、B、D可以表示为：

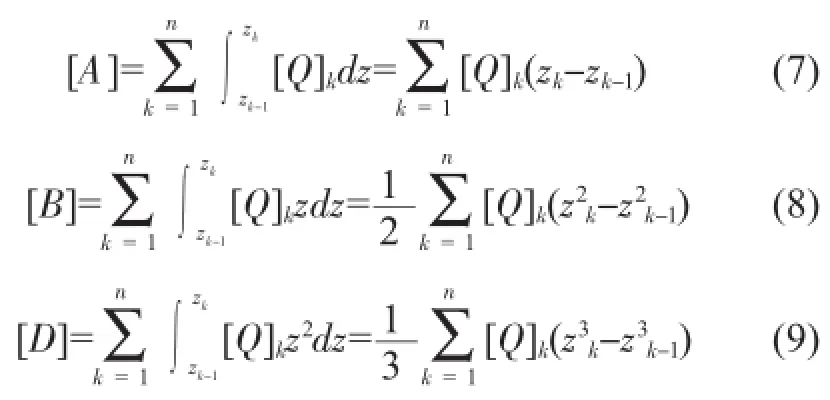
通过以上公式计算出曲率κ后，翘曲变形w的表达式为：

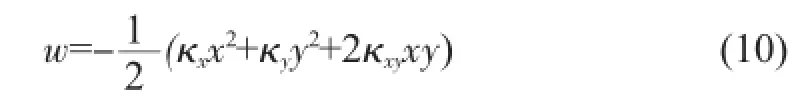
对于传统的翘曲计算模型，芯片所处层的材料参数根据芯片与塑封料的体积占比进行等效计算，得出该层的等效材料参数[5]，计算公式为：

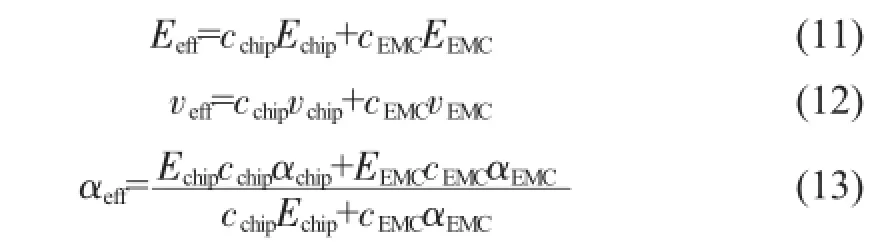
其中Eeff、veff、αeff分别是芯片层的等效弹性模量、泊松比、热膨胀系数；cchip、cEMC是芯片和塑封料的体积分数。通过等效复合材料的方法可以直接计算出封装结构的翘曲，记为weff。

但由于芯片所处的那一层中的芯片和塑封料属于两个不同的结构，最终封装产品表面在微观上其实有一定的曲率差别，如图1和图2所示。因此对于封装结构的曲率是一个分段的关系，可以表示为：

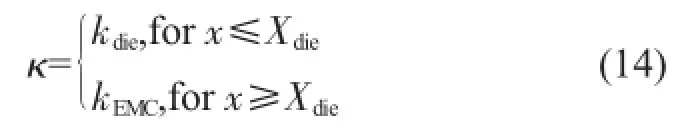
此处，kdie和kEMC分别是芯片和塑封料区域的曲率，x是从参考面中心点到所处位置的距离。经上述数值计算，对于正方形且相对较为对称的结构，曲率有κx≈κy、κxy≈0的关系。

对于芯片层部分的结构来说，芯片层边缘的翘曲值可表示为：

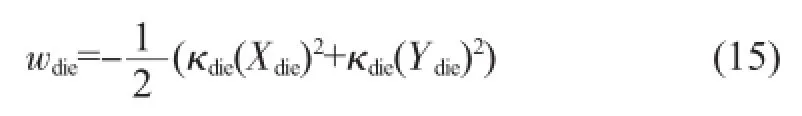
塑封料边缘部分的翘曲值为：

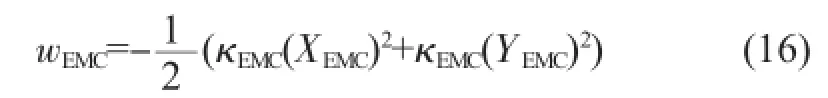
其中，Xdie和Ydie、XEMC和YEMC分布是芯片和塑封料尺寸的一半。最终的翘曲是由此双曲率共同作用的结果，本文采用芯片占比面积的加权平均，来计算最终的翘曲值，双曲率模型的翘曲计算公式为：

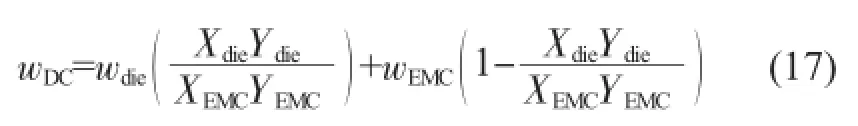
3 某指纹识别芯片的结构及材料参数

根据某指纹识别芯片的封装设计，其单颗产品的几何参数见表1。

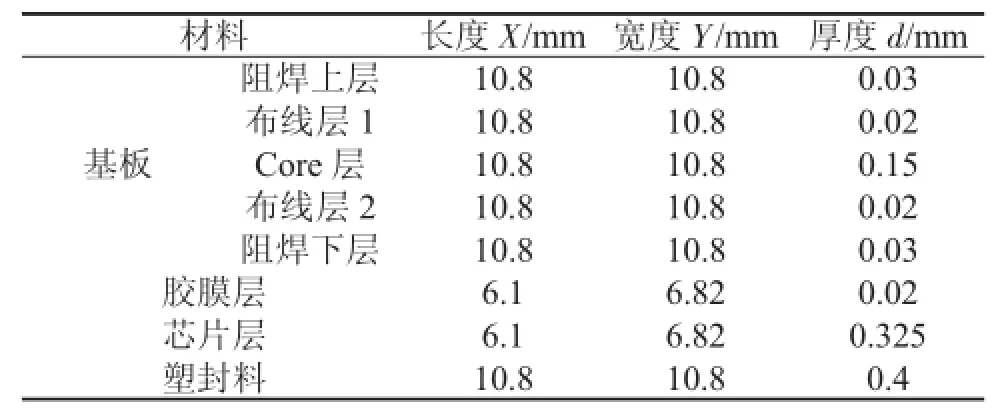
表1 封装结构外形尺寸

查询相关材料手册，该芯片结构使用的材料参数见表2。

将以上的结构和材料参数分布带入前述公式，就可以计算出曲率κ，进而可以求得封装结构的翘曲值。计算得出芯片部分的曲率κdie为8.79×10-4，塑封体部分的曲率κEMC为2.26×10-3。由于曲率的定义为圆半径的倒数，即，芯片部分的曲率较小，意味着芯片部分弯曲更为严重。

4 实验测量

为了验证多层板结构翘曲理论在芯片封装结构中的适用性，我们设计了上述芯片的样品，并采用Shadow moire测量了样品的翘曲状况。Shadow moire仪器（精度±1 μm）目前已经是测量芯片封装结构翘曲的一个通用仪器[9～10]，它采用不同波长的光线去照射样品表面，使用摄像头抓取图形，并对图形进行分析来得到样品的翘曲状况。我们随机选取了10颗样品进行了测量，翘曲平均值为31.7μm，测量的数据统计见图4。

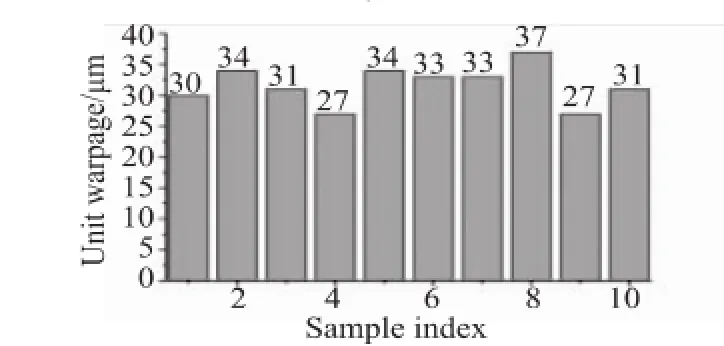
图4 使用Shadow moire对10颗样品测量的翘曲数据

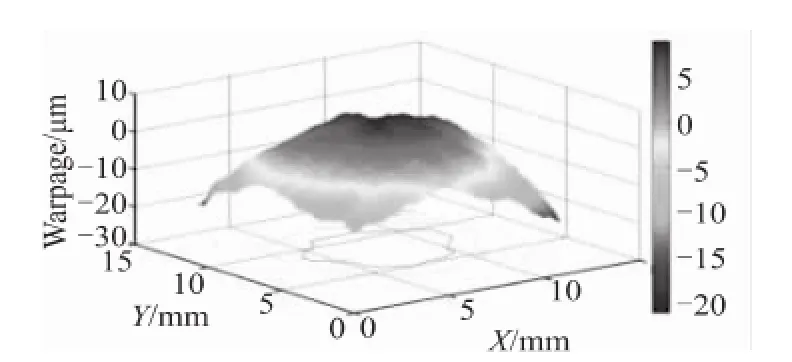
图5 使用Shadow moire测量样品1的三维翘曲形貌图

我们选取样品1的形貌图进行分析，见图5。从图5可以看出，封装结构中心的芯片部分有明显的凸起现象，弯曲现象严重，这也与前述理论公式的计算结果保持一致。

5 有限元仿真及理论分析

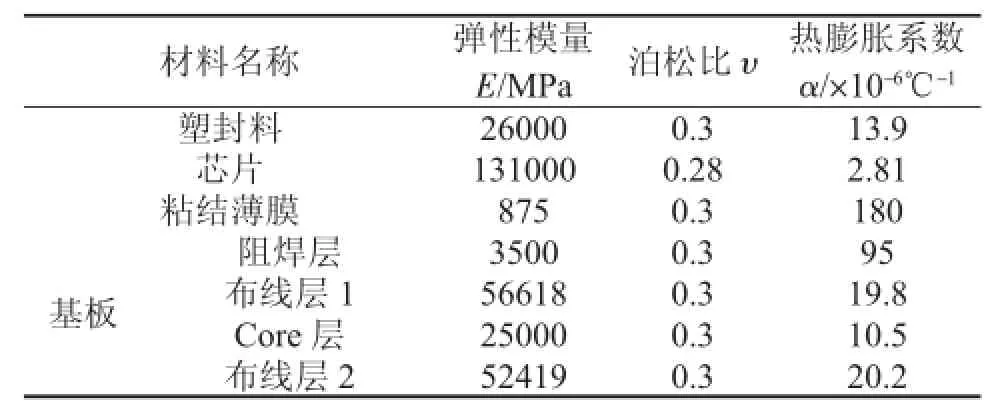
表2 封装材料参数表

为进一步验证上述理论，我们使用ANSYS 17.0对上述芯片封装结构翘曲问题进行模拟计算，对整个封装结构进行建模，如图6所示。

芯片在塑封完成后，会在175℃高温进行后固化烘烤（约5.5 h），长时间的高温烘烤可以使封装结构的内应力得到充分释放。而在降温至室温的过程中，由于材料参数的不匹配，上述结构会发生翘曲。因此对上述封装结构设置参考温度175℃，并对其整体施加温度为25℃的温度载荷，边界条件设置为自由边界。根据有限元计算的结果，最终翘曲最大变形量为35.2μm，翘曲变形云图见图7。

图6 ANSYS workbench芯片建模结果

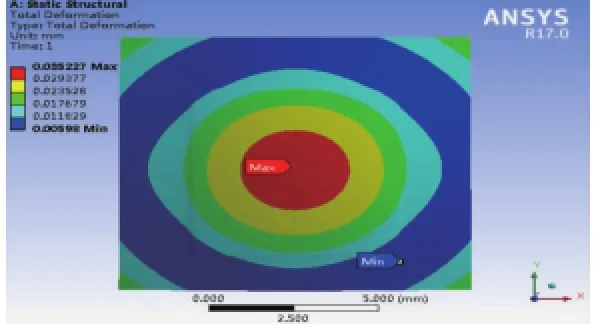
图7 室温（25℃）条件下的翘曲变形

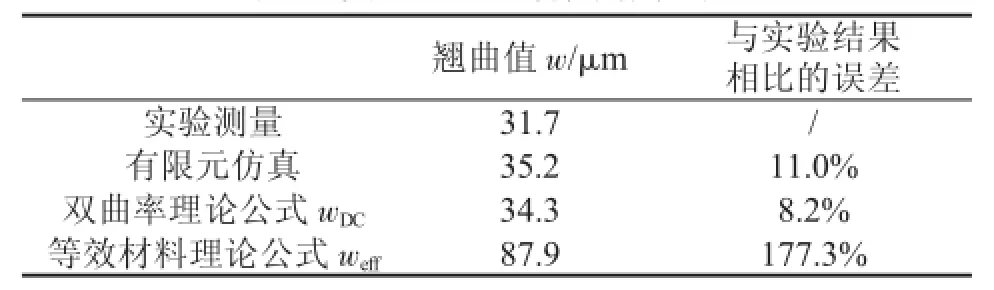
表3 实验-理论-仿真结果对比

实验测量、有限元仿真、双曲率公式wDC和等效复合材料公式weff的计算结果的对比见表3，由于实际样品在塑封及切割过程中，其边界条件并不是理想的自由边界条件，会受到一定的约束作用，所以翘曲值会偏小一些。而双曲率理论公式wDC和有限元仿真由于都是自由边界条件，其结果也更为接近，两者误差仅为2.6%，近似程度可以满足工程计算分析的要求。而等效复合材料公式的计算结果weff与实验测量相比误差较大，为177.3%，主要原因是传统的等效材料公式是基于芯片较小或者多芯片均匀分布的情况，而本样品的芯片尺寸和厚度均为封装尺寸的一半左右，采用等效材料的方式误差较大。

6 结论

本文提出了对于计算芯片封装结构翘曲变形的双曲率模型公式，将芯片封装结构简化为多层板模型，利用板壳理论，得到在自由约束边界条件下的翘曲变形解析表达式。以常规指纹识别芯片为例，结合实际样品测量及有限元仿真验证，均得到与理论一致的结果。该解析公式的近似程度可以满足常规指纹识别芯片封装评估分析要求，可以大量节省设计时的有限元建模及计算时间，对于快速并准确地评估封装结构有重要意义。本模型可以进一步延伸到其余可以简化为多层板的结构模型，对其余封装结构也具有参考价值。

[1]Suhir E.Predicted Bow of Plastic Packages of Integrated Circuit(IC)Devices[M].Thermal Stress and Strain in Microelectronics Packaging.Springer US,1993:951-972.

[2]Miremadi J.Impact of PBGA-ball-coplanarity on formation of solder joints[C].Electronic Components and Technology Conference,1995.Proceedings.1995:1039-1050.

[3]Hu K X,Yeh C P,Doot B,et al.Die cracking in flip-chip-on-board assembly[C].Electronic Components and Technology Conference,1995.Proceedings.IEEE,1995: 293-299.

[4]Ume I C,Martin T,Gatro J T.Finite element analysis of PWB warpage due to the solder masking process[J].IEEE Transactions on Components Packaging&Manufacturing Technology Part A,1997,20(3):295-306.

[5]Park S,Lee H C,Sammakia B,et al.Predictive Model for Optimized Design Parameters in Flip-Chip Packages and Assemblies[J].IEEE Transactions on Components& Packaging Technologies,2007,30(2):294-301.

[6]陈轶龙,贾建援,付红志,等.基于多层板弯曲理论的芯片翘曲变形分析[J].电子工艺技术,2012(6):330-334.

[7]Egan E,Kelly G,O'Donovan T,et al.A thermomechanical model for warpage prediction of microelectronic packages [J].International Journal of Microcircuits&Electronic Packaging,2005,25(1):100-118.

[8]黄克智.板壳理论[M].北京：清华大学出版社,1987.

[9]Ding H,Powell R E,Hanna C R,et al.Warpage measurement comparison using shadow Moire and projection Moire methods[J].IEEE Transactions on Components&Packaging Technologies,2003,25(4):714-721.

[10]Tsai M Y,Chang H Y,Pecht M.Warpage Analysis of Flip-Chip PBGA Packages Subject to Thermal Loading[J]. IEEE Transactions on Device&Materials Reliability, 2009,9(3):419-424.

A Predictive Model for Thermo -Mechanical Warpage of Micro-Electronic Packages

GUO Wei,WANG Xiaolong,XIE Jianyou,ZHANG Rui
（HuaTian Technology(Xi'an)Co.Ltd,Xi'an 710018,China）

The asymmetric structure and mismatch of coefficient of thermal expansion may lead to warpage of micro-electronic package due to the temperature change.The micro-electronic warpage may affect product reliability and quality.A fast predictive model for the package warpage is important for the design of package structure and material selection.The paper establishes a dual-curvature(DC)model to predicate the package warpage using the laminated theory.The samples are measured by Shadow moire and further verified by the finite element model.The experiment and simulation prove the accuracy of this model.In addition,this model can be further developed to predicate the warpage of other multi-layers structure,having a great potential for the package optimization.

chip warpage;finite element analysis;dual curvature

TN305.94;TN403

A

1681-1070（2017）01-0015-04

郭 威（1989—），男，陕西西安人，2015年毕业于西安交通大学，获硕士学位，现就职于华天科技（西安）有限公司，从事半导体封装结构的理论与仿真工作。

2016-8-5