大口径防爆弹弹带挤进过程仿真与分析

李 阳，卜雄洙，徐淼淼，关振华

(1.南京理工大学 机械工程学院，南京 210094； 2.中国兵器第二○八研究所， 北京 102202)

【装备理论与装备技术】

大口径防爆弹弹带挤进过程仿真与分析

李 阳1，卜雄洙1，徐淼淼1，关振华2

(1.南京理工大学 机械工程学院，南京 210094； 2.中国兵器第二○八研究所， 北京 102202)

防爆弹的弹带挤进过程是其在内弹道运动过程中的重要组成部分，弹带挤进时期的应力应变情况对提高火药气体密封、弹丸出膛初速等具有重要影响。根据Von Mises屈服准则，建立了防爆弹3D结构模型和材料模型看，利用显式动力学分析软件ANSYS/Explicit Dynamics对3D模型进行了有限元分析，得到挤进过程中弹带的应力集中区域和变形情况。根据受力平衡，计算了防爆弹动态挤进阻力。数值仿真实验结果为防爆弹弹带、身管设计提供了一定的理论依据。

挤进阻力；防爆弹；有限元法

弹带是防爆弹设计的重要部分。弹带结构的设计，影响到防爆弹在枪膛内起始扰动、火药燃烧时的密封、弹头出膛的初速以及弹头与枪膛的摩擦接触等各个方面[1]。随着防爆武器的发展，为设计出新型、高效的防爆枪械，研究防暴枪动态挤进过程中弹带的应力和变形情况，对改善防爆枪的弹带设计、提高身管寿命具有重要意义[2]。防爆武器属于非致命性武器，弹头材料与普通杀伤性武器不同，采用尼龙和塑料等材料[3]。弹带挤进压力、弹带在挤进时期变形的研究已有很多，但主要是针对各式火炮，针对防爆枪的弹带挤进过程研究较少[4-6]。本文以64 mm防爆弹为例，建立有限元模型，研究防爆弹在动态载荷作用下，弹带挤进阻力、弹带各结构上应力、应变随位移的变化。

1 防爆弹挤进模型有限元建模

1.1 几何模型的建立

为研究防爆弹的动态挤进过程，模型做如下假设[7]：

1) 不考虑卡膛过程，确定防爆弹的初始位置为弹带与坡膛初始接触；去掉身管内的膛线，减少单元数量，缩短计算时间。

2) 简化防爆弹上挤进过程中无关部位的细小特征，使有限元模型网格划分更加合理，计算时更易收敛。

3) 忽略发射时身管的后座、弹丸前端的空气阻力和弹丸本身的重力影响；不考虑挤进过程中的发热影响。

建立防爆弹3D挤进模型，防爆弹采用模型弹的结构，复杂内部结构以配重块代替，仿真时可将弹丸在身管内的运动看成是对称的。如图1所示。

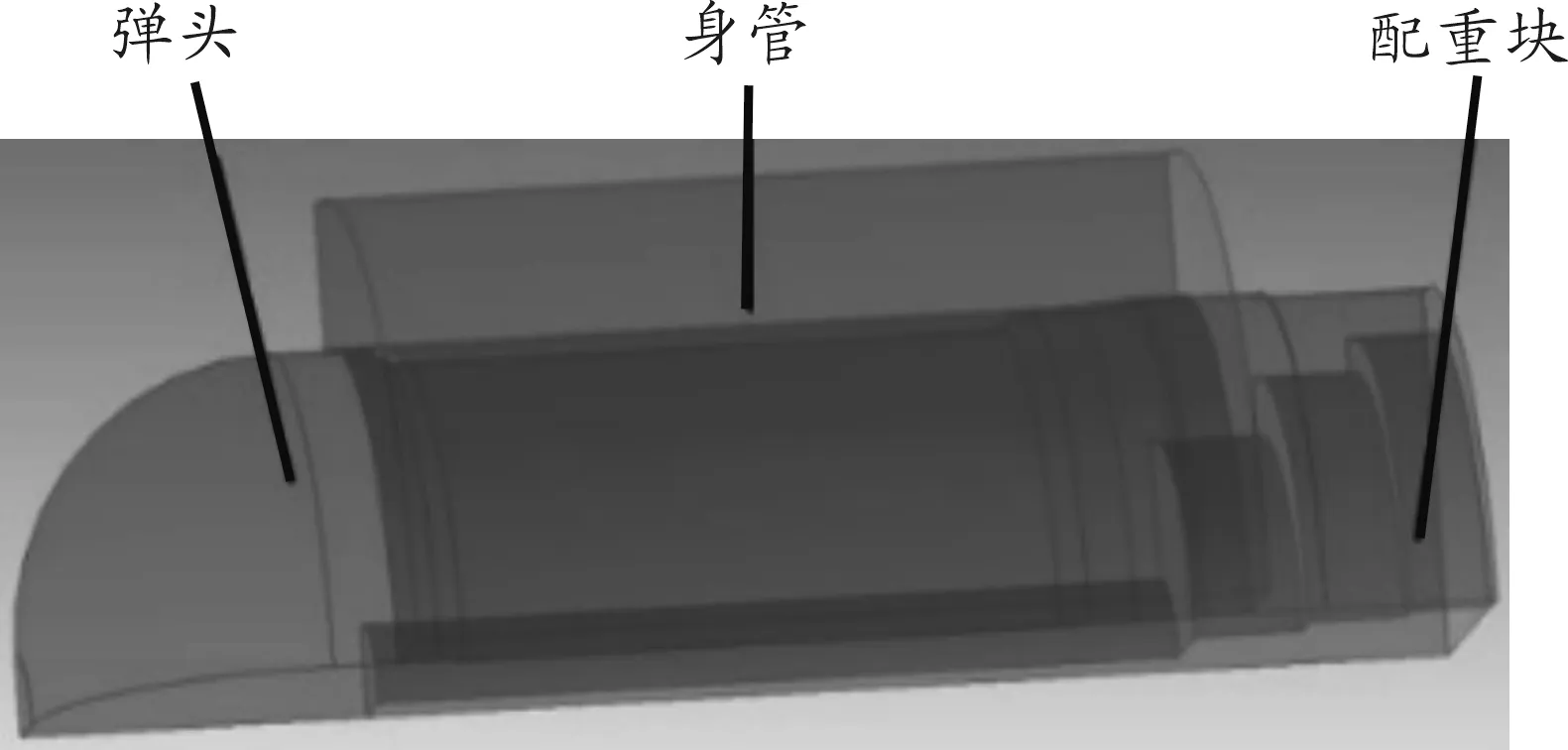
图1 防爆弹挤进1/4-3D模型

1.2 材料模型

针对防爆弹弹头材料的特殊性，弹头采用尼龙1010，身管材料采用高强度碳素钢50BA，配重块采用AL 6061-T6材料，材料的参数定义如表1[8]。

表1 模型材料参数设定

配重块和弹头采用经典的弹塑性材料本构模型，双线性等向强化(BISO)屈服模型

Y=Y0+AεP

(1)

其中：Y是材料的弹塑性材料屈服应力；Y0是材料的屈服强度；A是材料的切线模量；εP是材料的塑性应变。该模型适用于各向同性材料的大应变问题。

防爆弹高速冲击挤进分析中，因防爆弹和身管坡膛部分产生高速摩擦，会产生高温，并有大的塑性变形，且身管为金属材料适用Johnson-Cook屈服模型[9]：

(2)

1.3 网格划分

为了减少单元数量和节省计算时间，采用六面体为主导的网格划分法。挤进模型中由3个部件身管、弹头、配重块组成。试验中配重块和弹头通过螺纹和胶固定连接。因此，在网格划分时将弹头和配重块视为整体，其网格应保持相关性即在接触的边界上共用相同的节点。防爆弹的弹带结构不同于炮弹为单独结构，而是与弹头一体，如图2所示,为了增加弹带处计算精度，在弹带处对模型进行了细化。模型主要采用了完全积分的线性六面体单元C3D8，减少了沙漏效应，考虑到弹丸挤进过程中主要受到切向应力和正应力，不存在承受弯曲载荷的情况，因此不考虑单元剪切自锁现象。由于弹头模型的不是规则形状，在弹头内部还有少量的线性四面体单元C3D4，和线性楔形单元C3D6。

图2 模型网格细化

1.4 边界条件和载荷

根据实际挤进情况，在身管底面施加支撑条件，限制身管在弹丸运动方向的自由度，同时在身管外圈上限制径向自由度。由于防爆弹动态挤进过程复杂，防爆弹在挤进前已经历了火药燃烧推进加速卡膛的过程，防爆弹在挤进前即具有较高的运动速度。同时弹底压力随火药燃烧和防爆弹的挤进动态变化。不考虑卡膛过程，假设弹丸在挤进前初始速度为零，研究其在变化的膛压作用下，弹带在挤进过程中的应力与应变情况。防爆弹的弹底压力，按照防爆枪理论膛压曲线的形式，峰值取35 MPa，脉宽取4 ms[10]。

2 数值计算与仿真结果分析

防爆弹挤进模型采用显式动力学分析软件Ansys/explicit dynamics进行计算。软件在冲击信号不连续点处，通常得不到稳定的结果，为提高软件计算结果的稳定性设置了二次人工阻尼黏度系数，为减少噪声设置了线性人工黏度系数。

2.1 防爆弹在身管内的运动与受力情况

防爆弹在身管内的挤进过程，主要表现为弹带在身管内发生形变的过程，根据防爆弹弹带在身管内的挤进摩擦情况将防爆弹的挤进过程分为3个阶段，如图3所示。

图3 防爆弹在身管内的挤进过程

1) 起始位置，防爆弹弹带与坡膛初始接触；

2) 防爆弹的弹带在坡膛内运动,行程为L1段，L1=3.44 mm；

3) 防爆弹的弹带同时在坡膛和弹膛内运动,行程为L2段，L1=12.1 mm；

4) 防爆弹的弹带离开坡膛，只在弹膛内运动，即L2以后的行程，这里为L3。

防爆弹位移(L1+L2)=15.54 mm后，弹带全部进入弹膛，挤进过程结束。因此，在分析防爆弹挤进过程时只需观察30 mm位移内的防爆弹弹带上的应力、应变即可。

从仿真结果可见，防爆弹弹带在挤进过程受身管挤压与摩擦的等效应力集中区域，如图4所示。

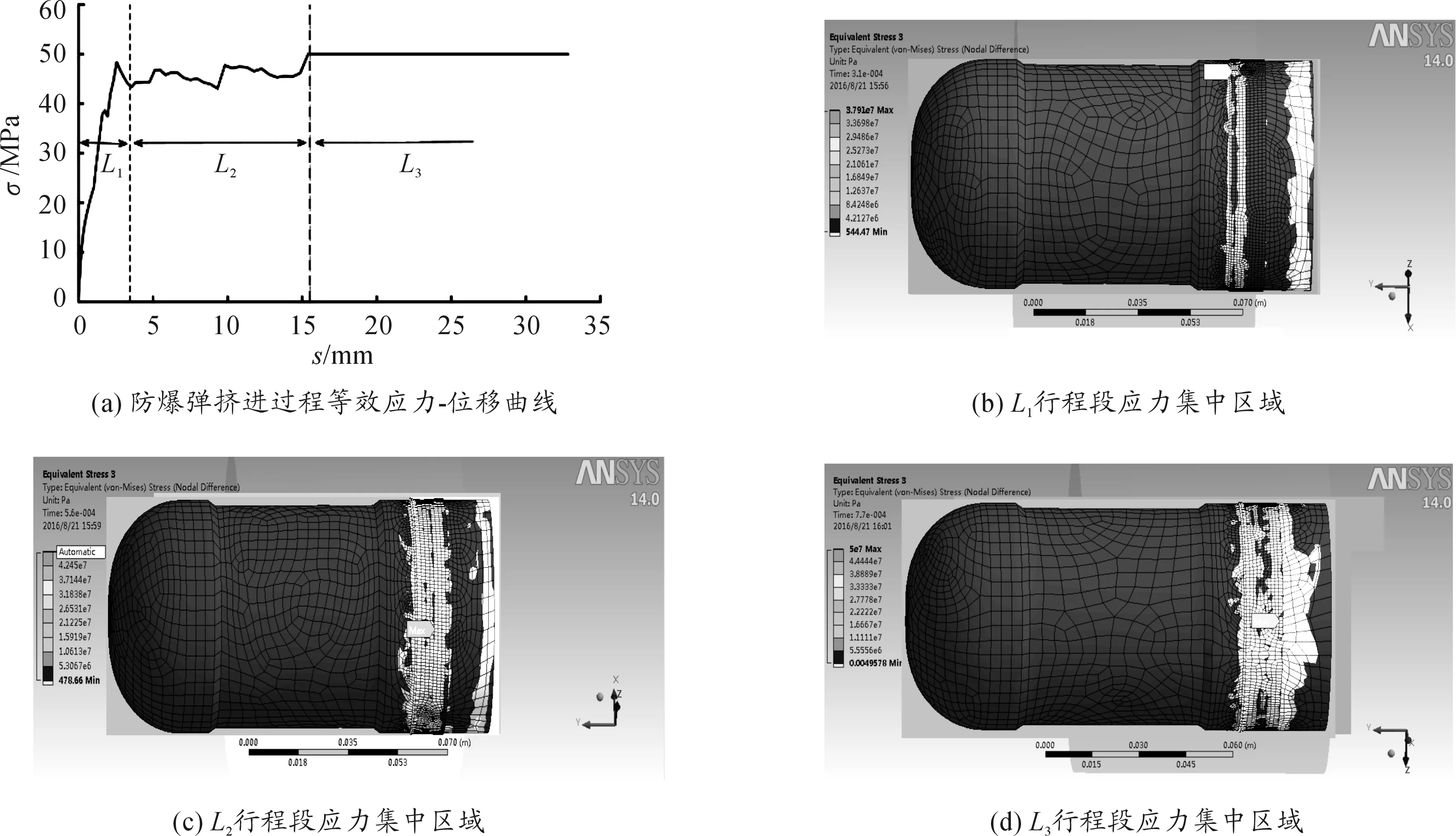
图4 各行程应力集中数值模拟示意图

在L1阶段，防爆弹由静止到开始挤进坡膛，应力集中在弹底和弹带前部，最大值为48 MPa。在L2阶段随着弹带离开坡膛进入弹膛中，弹带前端已发生明显的塑性变形，应力集中的部位向弹带中间移动，此时最大应力值为47.8 MPa。在L3阶段，弹带完全离开坡膛，进入弹膛，弹带的变形相对稳定，应力波动变小，应力达到最大值50 MPa。L1阶段：弹带由静止到开始进入坡膛，弹底压力上升，弹带前端材料的强迫量增大，应力集中现象快速发生在前端，见图4(a)中L1段；L2阶段：弹带已全部位于弹膛和坡膛中，弹带材料均已发生变形，此时随着弹带材料由坡膛进入弹膛，应力集中发生在弹膛入口处，应力集中部位开始向弹带中后部位移动；L3阶段:弹带完全进入弹膛内，弹带材料被身管挤压，有一个明显的向后流动,应力集中发生在了弹带尾部，此时整条弹带变形量达到最大，最大应力维持在一个较稳定的值[11-12]。

2.2 弹带各结构上应力、应变分析

为分析弹带各结构在挤进过程中的应力、应变变化，在弹带上沿运动方向取3个节点a、b、c分别位于弹带的前、中、后区域，如图5(a)。比较3个节点在挤进过程中的Von Mises等效应力、应变情况。

图5(b)中,左边一个垂直于s轴的虚线代表L1阶段的范围、其与第二根垂直的虚线之间代表L2阶段。弹带由坡膛进入弹膛的过程中，弹带前部a点应力、应变逐渐增大，应力极大值为13 MPa，a点应力增加的情况并不剧烈。弹带前部设计采用了斜面结构，在应力快速变化的情况下，使得材料应力和应变尽量减少，保证了弹带结构的稳定。弹带上b点处应力比a点大，应变相对平缓。弹带尾部c点应力、应变产生了一个快速变化由0.34 MPa上升到42 MPa，应力达到了一个极大值。首先，弹带尾部结构与前部不同，没有斜面设计；其次弹带在挤进过程中材料整体向后流动，使得弹带尾部产生了体积堆积，引起应力场的快速变化；同时当其由坡膛进入弹膛时，物理环境发生巨大改变，使弹带上的应变产生了阶跃的变化。3个节点的应变变化趋势与应力基本相同，只在b节点处应力极大时应变并不是很大。这是由于b节点位于弹带中部,前后单元形状类似，且变形时没有结构上的突变。

通过以上分析，在弹带前部设计斜面，有效地在应力突变的情况下，降低了最大应力。合适的斜面角度，可以使得弹带进入坡膛时应力变化较为稳定，不会产生结构上的损坏。其次，弹带在挤进过程中整体的形状沿挤进反方向变化，在弹带尾部堆积，应力、应变均发生极大变化，在弹带尾部c节点最大应力42 MPa接近材料的强度极限，此处为弹带上结构应力最大之处。

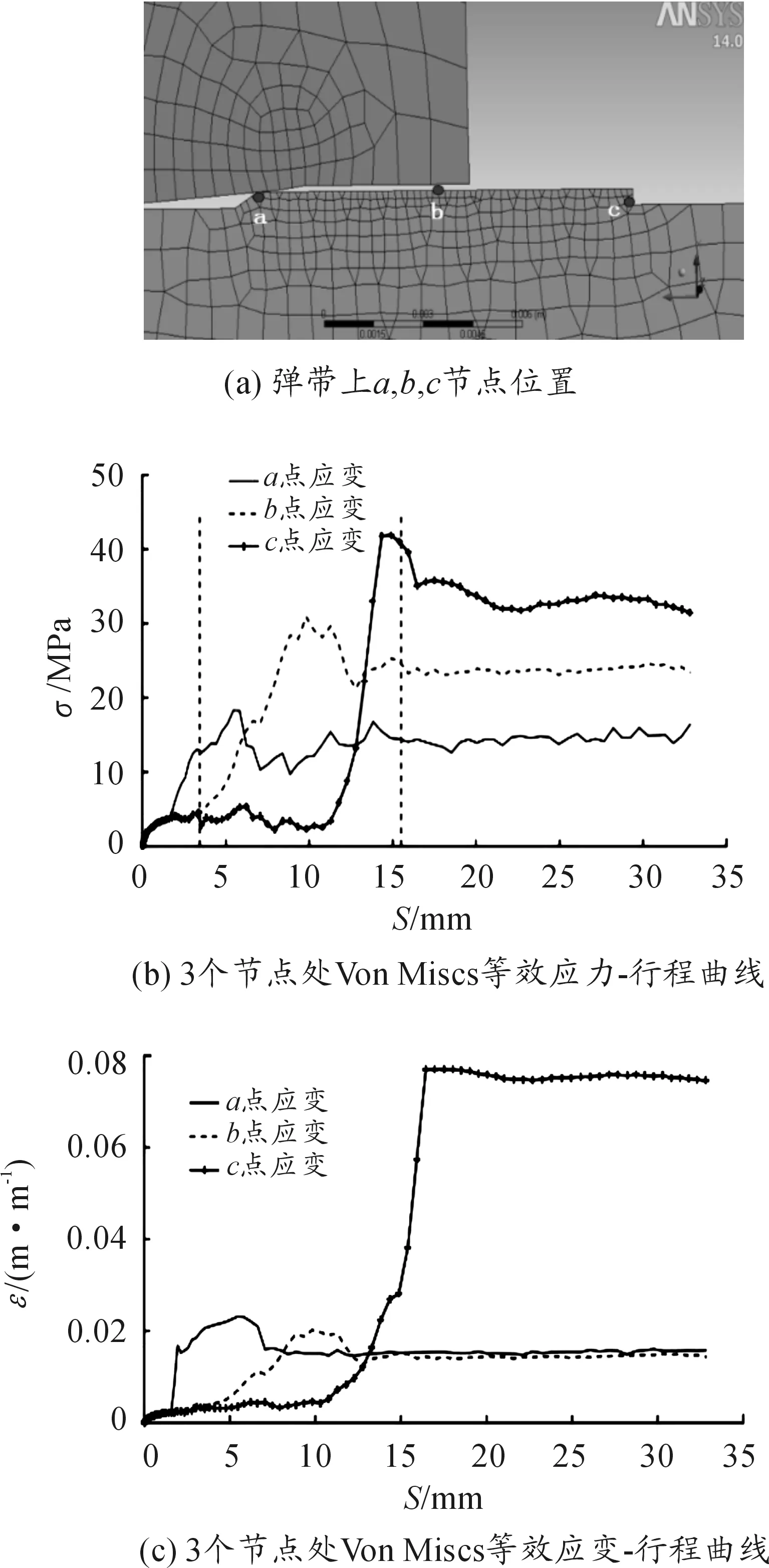
图5 弹带上前中后3个部位的应力σ、应变ε与行程s

2.3 弹丸挤进阻力的计算

防爆弹在运动方向上的受力平衡，根据牛顿第二定律，得到挤进运动过程方程[13]：

SDPD-Ma=FZ

(3)

其中：SD为弹底受力面积；PD为弹底压力；M为防爆弹质量；a为防爆弹在质心处节点的加速度；FZ为弹丸在挤进过程中受到的阻力。

数值模拟得防爆弹的质心节点处加速度与行程关系曲线如图6所示。

图6 防爆弹质心节点加速度-位移曲线

质心节点加速度代入式(3)，分段拟合得到防爆弹挤进阻力-位移曲线，如图7所示。

图7 挤进阻力-位移曲线

在图7，防爆弹受到的挤进阻力在L1、L2、L3阶段交界处附近发生突变，这是因为防爆弹在挤进过程中的运动环境发生突然改变，挤进阻力最大值为8.9 kN。

L1、L2为弹带的挤进阶段，此时随着弹带不断进入身管内，摩擦接触面积增大，同时弹带受力变形逐渐加剧，阻力不断上升。当弹带完全挤入弹膛时L3阶段，此时弹带与弹膛摩擦面达到最大，材料变形完全发生，阻力维持在较大的稳定值。

3 结束语

以64 mm防爆弹弹带挤进过程中弹带应力、应变为研究对象，针对模型不同材料分别采用了BIOS和Johnson-cook弹塑性本构模型，在有限元软件Ansys/Explicit中建立了弹带挤进过程的非线性动力学模型，利用显式算法解算有限元模型，得到在挤进过程中防爆弹弹带上的应力集中区域，同时分析了防爆弹在挤进过程中弹带各结构应力、应变情况，给出了防爆弹的挤进阻力和位移的关系曲线，为防爆弹弹带结构设计和优化提供了一定的理论依据。

[1] 顾文彬,赵有守,陶耀兴.尼龙弹带坡膛挤进过程中应力应变分析[J].弹道学报,1994(3):5-13.

[2] 孙全兆,杨国来,王鹏,等.某大口径榴弹炮弹带挤进过程数值模拟研究[J].兵工学报,2015,36(2):206-213.

[3] 关振华,朱平,孔斌.国产64mm防暴子母弹系列[J].轻兵器,2010(7):18-19.

[4] SOUTH JOSEPH，YIOURNAS ARISTEDES.A Study of the Engraving of the M855 5.56-mm Projectile [R]．[ S.l．]:[s.n.],2008.

[5] MA MING-DI,WS CUI,ZY ZENG,et al.Engraving process analysis of projectiles based on coupling of FEM and SPH[J].Vibration & Shock,2015,34(6):146-150.

[6] 陆野,周克栋,赫雷,等.坡膛结构参数对枪械内弹道挤进时期的影响研究[J].兵工学报,2015,36(7):1363-1369.

[7] 李宣荣.高速冲击挤进问题的瞬态有限元分析[D].西安:西安工业大学,2014.

[8] 米粮川,高树滋,赖长缨.内弹道弹带挤进过程仿真研究[J].弹箭与制导学报,2012,32(1):133-135.

[9] 邱从礼,侯日升,赵锋,等.考虑弹丸动态冲击条件下的内弹道性能研究[J].弹箭与制导学报,2014,34(4):140-142.

[10]刘文瑶,吴占文,李鹏军,等.防暴武器内弹道仿真计算软件研究[J].计算机仿真,2013,30(6):29-33.

[11]杨斌,张越.防爆弹丸挤进过程的弹丸变形应力[J].四川兵工学报,2011,32(9):13-14.

[12]肖攀.高速冲击挤进问题的动力学建模与瞬态有限元分析[D].南京:南京理工大学,2003.

[13]王鹏,杨国来,葛建立,等.基于Johnson-Cook本构模型的弹带挤进过程数值模拟[J].弹道学报,2015,27(2):55-61.

[14]胡慧斌，陈树肖，王洪波，等.弹带挤进膛线过程摩擦磨损试验及失效机理分析[J].火力与指挥控制，2015(12):167-170.

(责任编辑周江川)

Simulation and Analysis of Band Engraving Process for Large-Caliber Explosion-Proof Bullet

LI Yang1, BU Xiong-zhu1, XU Miao-miao1, GUAN Zhen-hua2

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2.No.208 Research Institute of China Ordnance Industries, Beijing 102202, China)

Explosion-proof bullet band engraving process is an important part of the interior ballistic moving process, and the engraving period of stress and strain have important effects on improving the propellant gas seal, the projectile muzzle velocity and so on. Firstly, according to the Mises Von yield criterion, we established the 3D structure model and material model. By using the explicit dynamic analysis software ANSYS/Explicit dynamics, we analyzed the 3D models and got the stress concentration and deformation region in the engraving process. Finally, according to the force balance, we computed the dynamic engraving resistance. The experimental results of numerical simulation provide a theoretical basis for the design of explosion proof and body tube.

engraving resistance; explosion-proof bullet; finite element method

2016-08-26；

2016-09-27

李阳(1988—)，男，硕士研究生，主要从事弹丸挤进压力测试研究。

10.11809/scbgxb2017.01.015

李阳，卜雄洙，徐淼淼，等.大口径防爆弹弹带挤进过程仿真与分析[J].兵器装备工程学报，2017(1):59-62.

format:LI Yang, BU Xiong-zhu, XU Miao-miao,et al.Simulation and Analysis of Band Engraving Process for Large-Caliber Explosion-Proof Bullet[J].Journal of Ordnance Equipment Engineering,2017(1):59-62.

TJ27

A