Bound States Energies of a Harmonic Oscillator Perturbed by Point Interactions∗
N.Ferkous and T.Boudjedaa
Laboratory of Theoretical Physics,Department of Physics,University of Jijel,PB 98 Ouled Aissa,DZ-18000 Jijel,Algeria
1 Introduction
In the past few decades,much attention has been paid to understanding and realization of one-dimensional quantum systems.The tremendous progress in nanotechnology has made it possible to obtain realizations of isolated onedimensional systems such as quantum wires,[1]Josephson junction arrays,[2]edge states in quantum Hall systems,[3]and nanotubes[4]see also the book.[5]From a theoretical point of view,the one-dimensional character makes the problem simple enough so that some complete solutions of particular quantum mechanical models could be obtained using specific methods.In addition,one of the important motivating factors for the study of these simple models was the extraction of physical insight that would be useful for the study of their higher-dimensional counterparts.
Spectral properties of the Schrödinger equation for the one-dimensional harmonic oscillator with one Dirac delta function have been studied by several authors.[6−9]This simple model has been used to describe the quark physics at small distances,in particular,the toponium physics.[10]In the present paper,we will consider the bound state energy problem of the one-dimensional harmonic oscillator plus two attractive point interactions of equal strength,by considering both momentum space and position space representations.This model could be regarded as a possible one-dimensional counterpart of the three-dimensional hydrogen molecule ion subjected to a static magnetic field in which the coulomb interactions are replaced by the corresponding one of simple point interactions.[11−12]The content of this work might be useful since the molecules,even the simplest diatomic molecules and their ionization are much more difficult to treat theoretically.
As we know,the bound state problem for one dimensional Hamiltonian that involves delta function potentials has an exact implicit solution whenever the eigenvalue problem without the delta function potentials can be solved exactly.In this context,we determine the exact transcendental energy bound state equation for the aforementioned one-dimensional harmonic oscillator perturbed by two attractive Dirac delta potentials,using Green’s function techniques which are widely recognized as a powerful mathematical tools suitable for obtaining solutions of complex interacting systems.[13]
Recently,the multidimensional quantum harmonic oscillator with point interactions problem has attracted great interest in connection to few body systems,especially in view of recent experiences in the field of ultra-cold atoms.[14−16]In these experiments neutral atoms are first cooled to extremely low temperatures(of the order nano-Kelvin)and then confined in an optical lattice formed by standing wave laser beams.Typically,the lattice sites that confine these atoms can be considered as harmonic oscillator potentials.The physical interaction between two ultra-cold atoms is replaced by a point interaction potentials to avoid the complications of a realistic atom-atom interaction.However,if we try to solve the problem of quantum harmonic oscillator with point interactions for more than one dimension,divergent sums appear and one needs a regularization scheme to extract a meaningful result for the energy bound states.[17]In this paper,we will use an exponential regulator to deal with this divergence,the idea of this technique is inspired from that used to remove divergence appeared when considering the Casimir effect.[18−19]The result obtained here is consistent with
The further content of this paper will be as follows.In Sec.2,We present a new momentum space approach to the one-dimensional harmonic oscillator perturbed by a single point interaction by transforming the problem to an inhomogeneous differential equation.In Sec.3,we determine explicitly the exact transcendental equation for the energy of the one-dimensional harmonic oscillator plus two attractive delta functions in momentum space by considering both even and odd states solutions.Then,we deduce the corresponding limiting cases.In Sec.4,we enrich our study by considering the system treated in Sec.3 in position space using some properties of the Green’s function.In Sec.5,we consider the Schrödinger equation for harmonic oscillator plus Dirac delta potential in more than one dimension.We will introduce an exponential regulator to deal with divergent series and then we redefine the strength of the Dirac delta potential to absorb the dependence on the regularization parameter.Some concluding remarks are reported in the last section.
2 One-Dimensional Harmonic Oscillator Perturbed by a Single Point Interaction
Let us consider a particle of a massmsubjected to a harmonic oscillator potential of frequencyωand perturbed by a single point interaction represented by delta function potential.The system is described by the following Schrödinger equation

for the bound stateα>0.In the momentum representation this equation takes the form

To transform Eq.(2)to inhomogeneous differential equation,let us define the numbercas

thus,Eq.(2)reads

with the abbreviations

Let us recall that the eigenstatesφn(p)corresponding toα=0,(i.e.,γ=0),form a complete set of states for the simple harmonic oscillator.
We consider now the Fourier transform between the positio
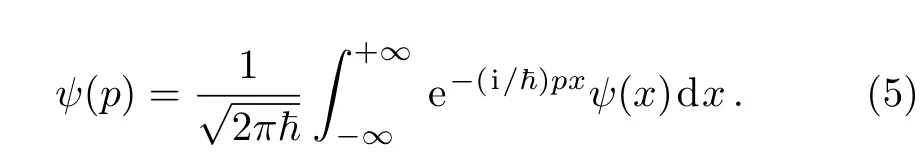
First,it is well known that the eigenstates of a nondegenerate even operator have definite parity;they are either even or odd.Then,since the Fourier transform preserves the parity of the wave function,ψ(p)should have a definite parity.[20]In addition,the delta function has no effect on odd states because in this casec=0.Hence the solution to the previous equation can be found by expandingψ(p)as

whereφ2n(p)are given in terms of Hermite polynomials by[21]

in whichλ=1/ħmωand its corresponding eigenvalues

As the second member of the inhomogeneous equation(4)is a constant,therefore,the wave functionψ(p)is given by

whereG(p,p′)is the Green’s function for the homogeneous part of Eq.(4).In the present case,it reads as

Inserting Eq.(9)in Eq.(3),the bound state energy is given simply by the condition

The Green’s function(10)can be written explicitly as

whereσ=1/2−E/ħω.Therefore,Eq.(11)reads

Then,by using the following formula[22]
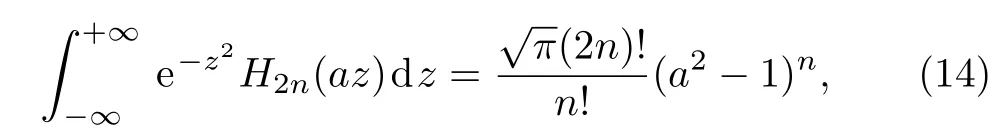
thus,Eq.(13)becomes

Noting that
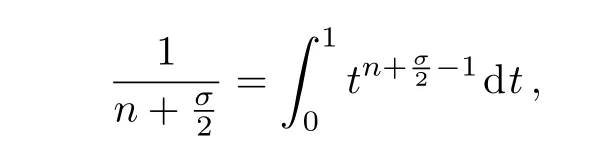
and using the doubling formula[22]
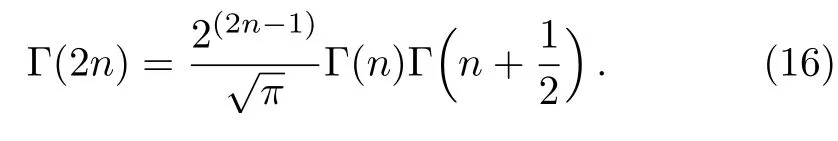
Equation(15)can be written as
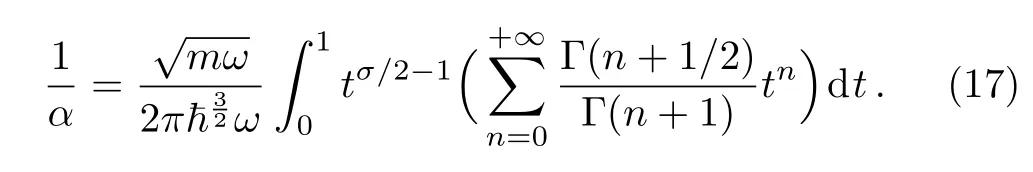
Then,with the help of the binomial formula

and performing the integral,we get the transcendental equation

we obtain therefore the same result as that found in position space.[6]
To end this section,let us recall some special cases.First,forα=0,the right hand side of Eq.(19)diverges.This divergence is matched by poles of the gamma function in the numerator
and consequently we recover the energy spectrum for even eigenstates
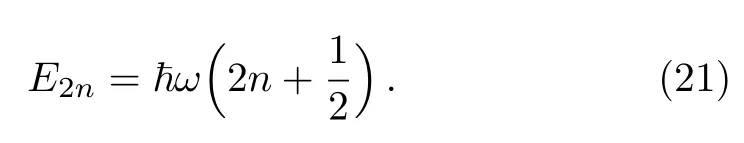
Forω=0,one can use the asymptotic behavior of the gamma function described by the famous Stirling formula[22]

to obtain the well known single energy bound state for the Delta potential well as

3 One-Dimensional Harmonic Oscillator Perturbed by a Double Point Interactions
Let us now consider a system described by two attractive delta functions of strength−α<0,separated by a distance 2aand subjected to a harmonic oscillator potential.The Hamiltonian is then expressed as

In the momentum representation,the Schrödinger equation corresponding to the Hamiltonian(24)takes the form

where
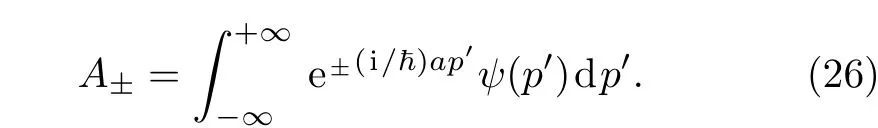
Thus Eq.(25)can be rearranged as
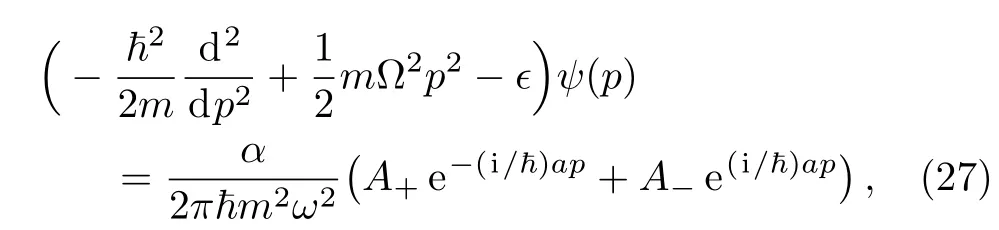
withϵ=E/m2ω2and Ω =1/m2ω.
3.1 Even State Solution
Ifψ(p)is an even function,therefore,it can be written only in terms of even eigenstates

in this case we haveA+=A−.Therefore,the wave functionψ(+)(p)is given by

in which the Green’s function for even eigenstates,G+(p,p′),has the same expression as described in the previous section.
To obtain the energy eigenvalues,we insert Eq.(29)in Eq.(26)we get

by using Eq.(12),the last expression is explicitly written as

in whichλ=1/ħmω.To perform these integrals,we use the formula[22]

we obtain

whereσ=1/2−E/ħω.Noting that
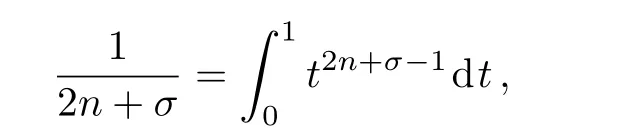
thus,Eq.(33)can be written as

now,we use the formula[23]
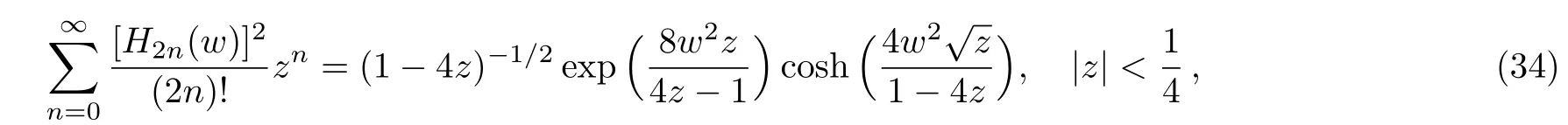
we get

the integral on the right hand side of Eq.(35)can be evaluated in closed form in terms of parabolic cylinder functions(see Appendix),we obtain

Equation(36)represents the transcendental equation of the energy eigenvalues for even state solution.
3.2 Odd State Solution
Ifψ(p)is an odd function,then it can be expressed in terms of odd eigenstates

in this case we haveA+=−A−.Then,the wave functionψ(−)(p)is given by

whereG−(p,p′)is given in terms of odd eigenstates as

which can be written explicitly

whereκ=3/2−E/ħω.
Now,inserting Eq.(38)in Eq.(26)and using the Green’s function(40)we obtain the following expression
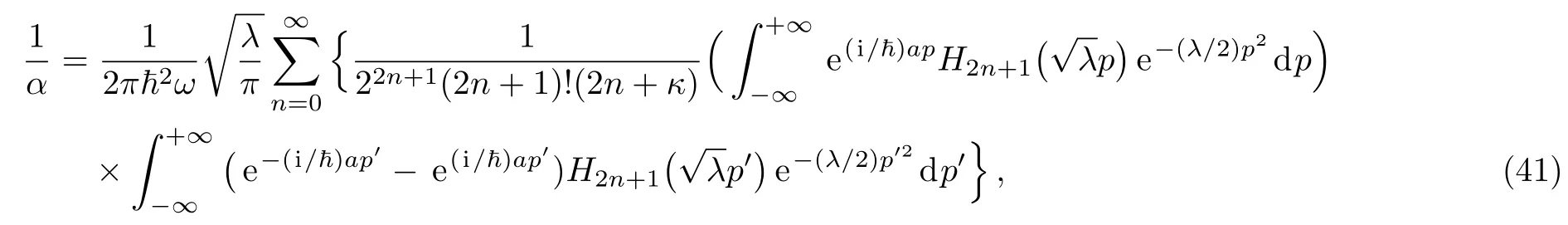
then,we apply the formula[22]

we obtain
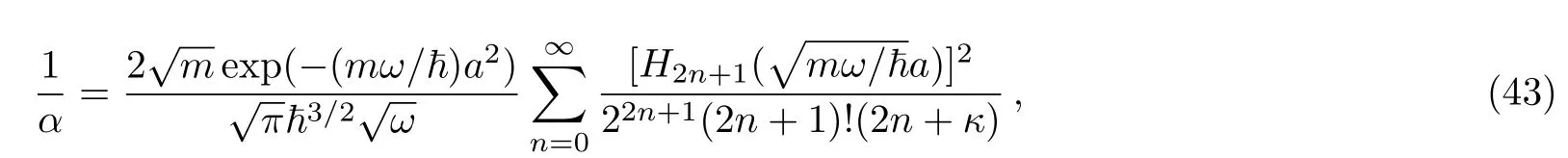
noting that

thus,Eq.(43)can be written as
and with the help of the formula[23]

Equation(45)is then written as

the integral on the right hand side of Eq.(47)can be evaluated in closed form(see Appendix)and we obtain
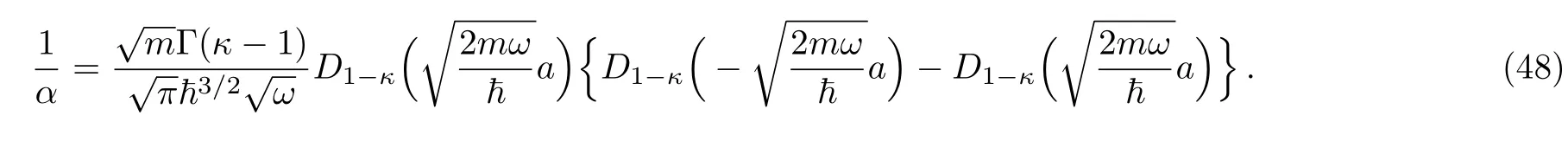
Equation(48)represents the transcendental equation of the energy eigenvalues for odd state solution.This equation is valid only fora/=0 since fora=0 the delta potential has no effect on odd state.
3.3 Special Cases
As a check of the above results,let us consider some special cases.
First,we consider thea→0 limit,in this case the parabolic cylinder function is reduced to[22]

Thus,Eq.(36)is simplified to

then,the doubling formula given by Eq.(16)simplifies the last expression to

which is the same result as the previous section by replacingα→α/2.
Now we consider theω→0 limit. In this case,σ=1/2−E/ħωbecomes very large.The parabolic cylinder function for large order behaves as[24]


therefore,the transcendental equation for even states(36)reduces to where we have again used the doubling formula given by Eq.(16).Then,with the help of the Stirling formula Eq.(22),the last equation is simply written,forω→0,as

in which we have setk2=−2mE/ħ2.Equation(52)represents the bound states condition for the double deltafunction potential well for even state.[25−26]
In addition,theω→0 limit of the transcendental equation(48)for odd state can be obtained by similar steps as

thus,one recovers the bound state condition for the double delta potential well for odd state.
4 Position Space Treatment
To enrich further the content of the current study,we consider in this section the system described by the Hamiltonian(24)in the position space.For this goal,we begin by writing the corresponding inhomogeneous Schrödinger equation as

The Green’s function reads
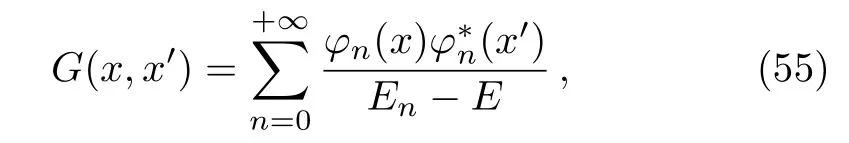
where the eigenstatesφn(x),corresponding toα=0,are given as[27]
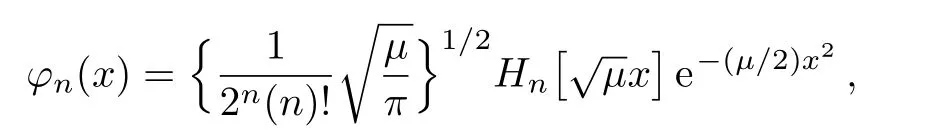

withµ=mω/ħ,and the discrete eigenvaluesEn=ħω(n+1/2).
We can write the solutionψ(x)in terms ofG(x,x′)as
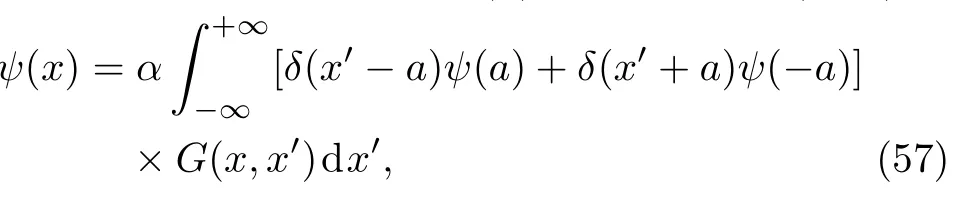
and hence we obtain

First,it is straightforward to see that the Green’s function satisfies the following two properties
i)Sinceφn(x)is real thenG(x,x′)is symmetric

ii)The Green functionG(x,x′)is an even function sinceφn(x)have a definite parity

4.1 Even State Solution
As mentioned above,the even solution is written as∑

the corresponding Green’s function,G+(x,x′),satisfies,in addition to properties(59)and(60),the relation

Therefore,for even solution,Eq.(58)is reduced to
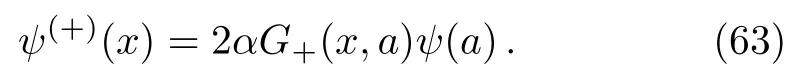
Now,taking the limitx=a,the energy eigenvalues are determined from the following equation
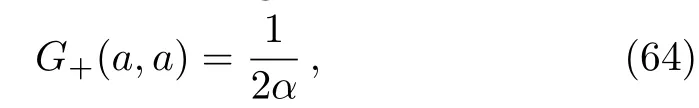
where the Green’s functionG+(a,a)is expressed as

which can be written by means of the expression(56)as
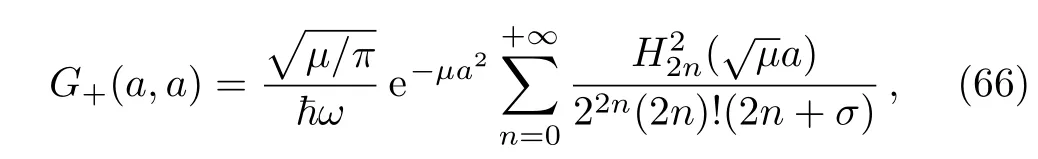
withσ=1/2−E/ħω.From Eq.(66)and Eq.(64)we obtain

As one can see,the last expression is the same as Eq.(33)and we will eventually arrive at the same transcendental equation(36).
4.2 Odd State Solution
The odd solution reads
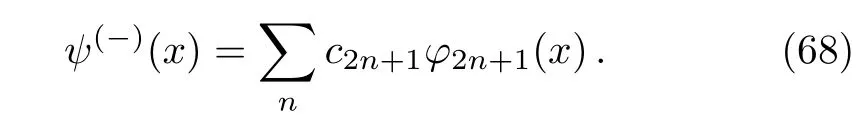
In addition to properties(59)and(60),the correspondingG−(x,x′)satisfies

From Eq.(58),the odd solution can be written in terms of the Green’s function as
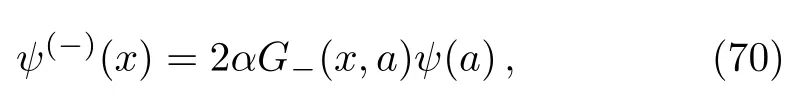
taking the limitx→a,the eigenvalues are determined from

where the Green’s functionG−(a,a)is
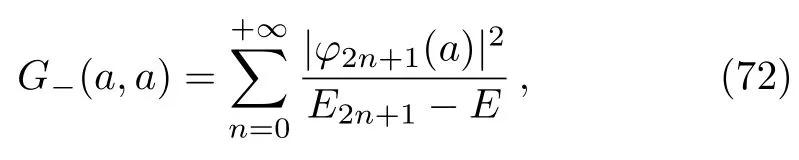
which can be written explicitly

whereκ=3/2−E/ħω.

Again,the expression(74)is the same as Eq.(43)and we will of course arrive at the same transcendental equation(48).
To end this section,let us mention that a solution to the transcendental equations(36)and(48)can be given graphically for specific values of the parameters.
5 Multidimensional Case
As discussed in the introduction,a system formed by two confined ultra-cold atoms of massµin interaction is described by the following Hamiltonian

wherer1andr2are the position vectors of the two atoms.This Hamiltonian can be separated into a center of mass part and a relative part via the transformation

and its corresponding canonical momentumpandP,we thus obtain
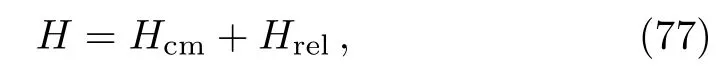
where
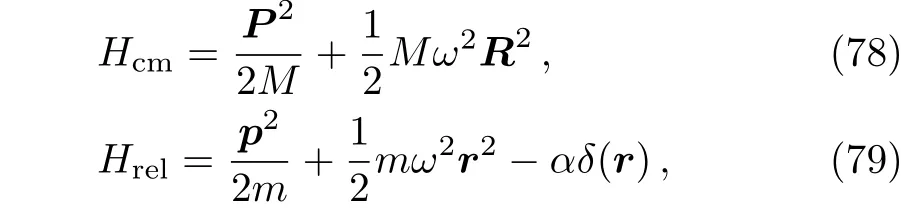
in whichM=2µandm=µ/2.
As the solution of the center of mass part is well known,we will focus our attention on the relative part which represents a harmonic oscillator perturbed by a point interaction.The Schrödinger equation corresponds to the Hamiltonian(79)can be written as

Following similar steps as the previous section,one arrives to the following condition for the bound states energies

where the Green’s functionG(0,0)reads

with the eigenstatesφn,ℓ,m(r)for theD-dimensional isotropic harmonic oscillator given explicitly by[28]

in whichλ=mω/ħ,αℓ(αℓ+1)=ℓ(ℓ+D−2),Lνnthe associated Laguerre polynomials and Λmℓ(Ω)are the hyperspherical harmonics.The corresponding eigenvalues
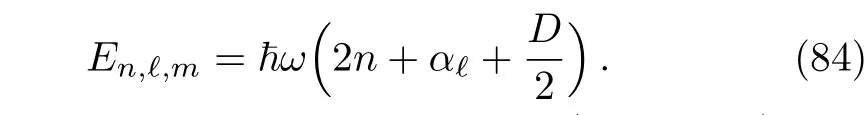
It is easy to note that only the s-waves(i.e.,ℓ=0)contribute to Eq.(81).Using the formula[22]


the relation(81)reads whereσ=D/2−E/ħω.As one can see,the series on the right-hand side of the last expression diverges forD≥2 since it behaves like a Riemann series for large values ofn:

To remove this pathology,we need a regularization scheme.To this aim,we will introduce an exponential regulator where the general idea of this technique is inspired from that used for dealing with divergences appeared when considering the Casimir effect.[18−19]Thus,we rewrite the expression(86)as
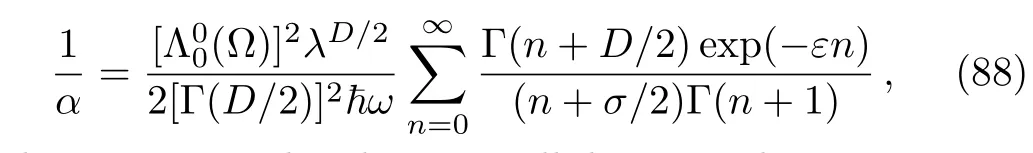
whereεis considered as a small dimensionless parameter.Therefore,the resulting series can be expressed in terms of the hypergeometric function,namely

Eq.(88)becomes
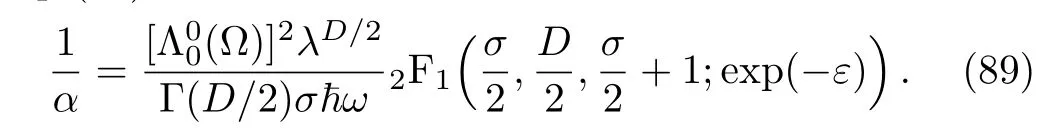
First,we note that forD=1 andε→0,we obtain the result(19)of the Sec.2.In addition,the series diverges forD≥4 and converges forD<4.
First,we consider the caseD=3.One can use the following relation[22]to leading order inε

we obtain

in this case,the expression(89)reads

As the energy is a physical observable it should be independent of the extra parameterε.The dependence on this parameter can be absorbed in a redefinition of the parameters of the theory

The constantαRis defined as a finite quantity.Therefore,Eq.(92)reads in whichσ=3/2−E/ħω.
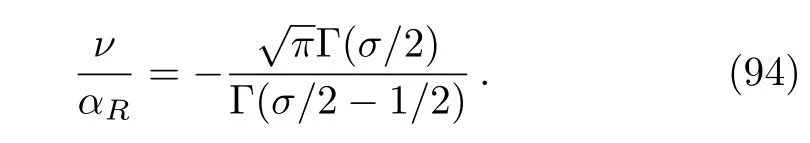
The expression(94)represents the transcendental equation for the energies bound states related to the problem(80)for the relative part with normalized strengthαR.This result is similar to that found by Bush[17]where the Dirac delta potential,for the same problem has been replaced by a regularized form,namely
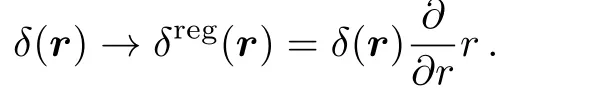
For the caseD=2,the expression(89)reads

with Sinceεis a small parameter,we can use the following approximation formula[24]

whereγis the Euler constant andψis the digamma function,we obtain

in whichβ= ħ2/m.In order to make the theory finite we introduce the renormalized coupling constant

we therefore obtain the transcendental equation with normalized strengthαras

Finally,let us mention that whenω→0,i.e.,σ≫,we obtain from the transcendental equation(94)the binding energy,forD=3,as

where we have used the Stirling formula(22).
ForD=2,we use the fact thatψ(z)∼ln(z)forz≫.Thus,we obtain from(97)the following expression for the energy bound state

in which we have used the notationε=(ω/ω0)¯εfor convenience,and¯εis a small dimensionless parameter.
Equations(100)and(101)represent the bound states energies for a nonrelativistic particle subjected to 3D and 2D Dirac delta potential respectively.The results are in agreement with Refs.[29–31].
6 Conclusion
In summary,we have used the momentum space representation to derive an exact transcendental bound state energy equation for one-dimensional harmonic oscillator perturbed by a single and double attractive delta functions via Green’s function techniques.We have considered the even and odd solutions of the system and their corresponding limiting cases.We have also considered the problem in the position space and we have shown that we obtain the same transcendental equations as expected.
For a system described by a harmonic oscillator plus delta function potential in two or more dimensions,divergent series appear.We have introduced an exponential regulator to deal with this divergence and we have succeeded to give the transcendental equation for the energies bound states for the problem.The result of this paper essentially agrees with Ref.[17]forD=3 in which the authors have replaced the Dirac delta potential by a regularized form.
In closing let us also mention that the problem of the two-and three-dimensional harmonic oscillator potential plusδ-function systems is considered in[34]by incorporating a different renormalization scheme and the self-adjoint extension method.
Appendix
(A)The integral corresponding to the even solution
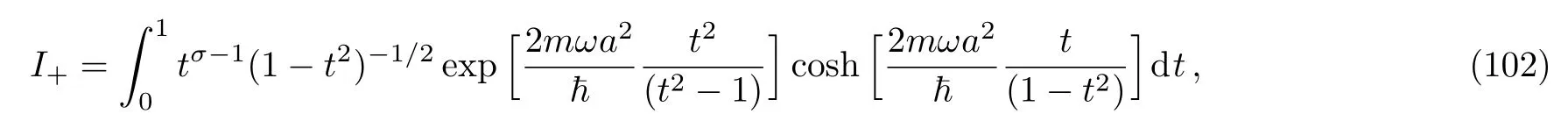
can be simplified as

where
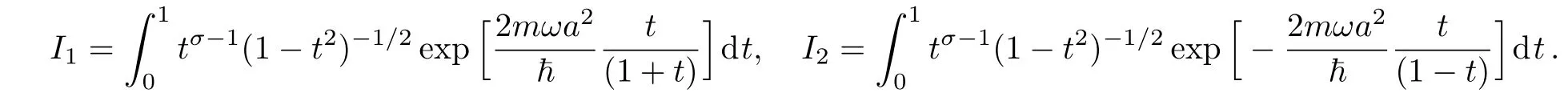
To perform the integralI1,we use the changet2=1−u,we obtain

then,we use the integral formula for the product of two parabolic cylinder functions[32]
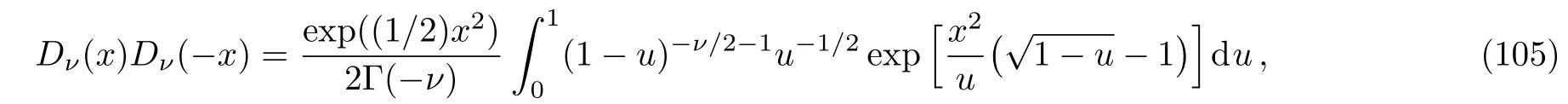
thus

To perform the integralI2,we use the changes=t/(1−t),the integralI2is transformed into
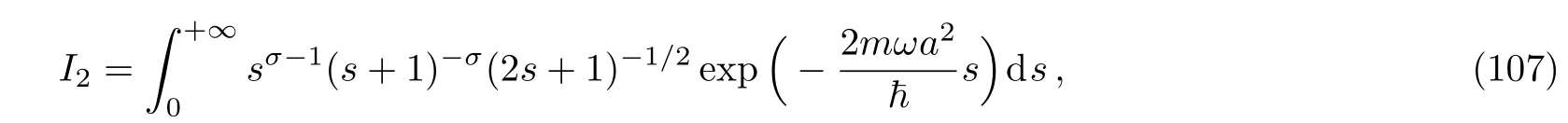
then,we use the formula[33]

therefore,we obtain
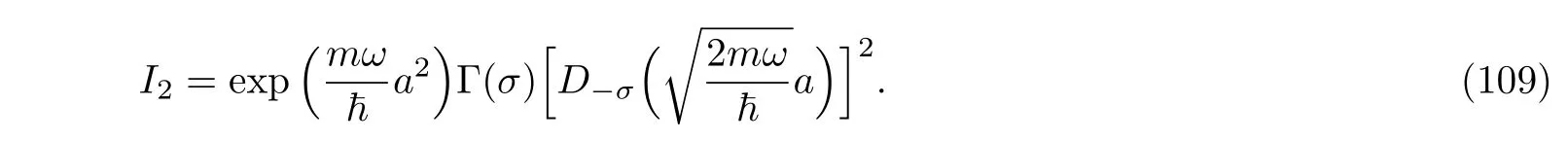
Substituting Eqs.(106)and(109)into(103),we get
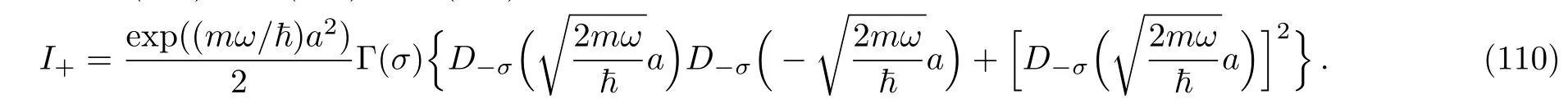
(B)The integral corresponding to the odd solution

this integral can be simplified to

where

Obviously,these are the same integrals as above just one replacesσ→κ−1.Thus,we obtain

[1]A.Yacoby,H.L.Stormer,N.S.Wingreen,et al.,Phys.Rev.Lett.77(1996)4612.
[2]A.van Oudenaarden and J.E.Mooij,Phys.Rev.Lett.76(1996)4947.
[3]W.Kang,H.L.Stormer,L.N.Pfeiffer,K.W.Baldwin,and K.W.West,Nature(London)403(2000)59.
[4]P.L.McEuen,M.S.Fuhrer,and H.Park,IEEE Trans.Nan-otechnol.1(2002)78.
[5]T.Giamarchi,Quantum Physics in One Dimension,Oxford University Press,Oxford(2004).
[6]D.A.Atkinson and H.W.Crater,Am.J.Phys.43(1975)301.
[7]O.Olendski,J.Phys.Condens.Matter 7(1995)5067.
[8]S.H.Patil,Eur.J.Phys.27(2006)899.
[9]J.Viana-Gomes and N.M.R.Peres,Eur.J.Phys.32(2011)1377.
[10]M.P.Avakian,G.S.Pogosyan,and A.N.Sissakian,Phys.Lett.A 124(1987)233.
[11]G.V.Dunne and C.S.Gauthier,Phys.Rev.A 69(2004)053409.
[12]I.R.Lapidus,Am.J.Phys.38(1970)905;I.R.Lapidus,Am.J.Phys.50(1982)453.
[13]E.N.Economou,Green’s Functions in Quantum Physics,Springer-Verlag,Berlin(1979).
[14]C.C.Tannoudji,Rev.Mod.Phys.70(1998)707.
[15]A.Aspect,E.Arimondo,R.Kaiser,N.Vansteenkiste,and C.C.Tannoudji,Phys.Rev.Lett.61(1988)826.
[16]T.Stöferle,H.Moritz,K.Günter,M.Köhl,and T.Esslinger,Phys.Rev.Lett.96(2006)030401.
[17]T.Bush,B.G.Englert,K.RzaSewski,and M.Wilkens,Found.Phys.28(1998)549.
[18]J.R.Ruggiero,A.H.Zimerman,and A.Villani.Rev.Bras.Fis.7(1977)663.
[19]K.A.Milton,The Casimir Effect:Physical Manifestations of Zero-Point Energy,World Scientific,Singapore(2001).
[20]N.Zettili,Quantum Mechanics:Concepts and Applications,2nd ed.,John Wiley and Sons(2009)p.129.
[21]M.Chester,Primer of Quantum Mechanics,Krieger,Malabar,FL(1992).
[22]I.S.Gradshteyn and I.M.Ryzhik,Table of Integrals,Series,and Products,Elsevier,Amsterdam(2007)pp.896,895,1031,1009,1028.
[23]Y.A.Brychkov,Handbook of Special Functions:Derivatives,Integrals,Series and Other Formulas,CRC Press,New York,NY,USA(2008)p.493.
[24]M.Abramowitz and I.A.Stegun,Handbook of Mathematical Functions with Formulas,Graphs,and Mathematical Tables,10 printing,U.S.Government Printing Office,Washington,D.C.(1972)pp.687–689,559.
[25]S.Gasiorowicz,Quantum Physics,3nd ed.,John Wiley&Sons,New York(2003).
[26]M.Belloni and R.W.Robinett,Phys.Rep.540(2014)25.[27]S.Flügge,Practical Quantum Mechanics,2nded.,Springer,Berlin(1994)p.107.
[28]K.J.Oyewumi and E.A.Bangudu,Arab.J.Sci.Eng.28(2A)(2003)173.
[29]R.M.Cavalcanti,Rev.Bras.Ens.Fis.21(1999)336.
[30]N.Ferkous,Phys.Rev.A 88(2013)064101.
[31]B.R.Holstein,Am.J.Phys.82(2014)591.
[32]C.A.Malyshev,Integr.Transf.Spec.F 14(2003)139;D.Veestraeten,Some Integral Representations and Limits for(Products of)the Parabolic Cylinder Function,E-print arXiv:1505.01948v2.
[33]A.P.Prudnikov,Yu.A.Brychkov,and O.I.Marichev,Integrals and Series,Vol.1,Translated from the Russian by N.M.Gueen,Gordon and Breach Science Publishers,New York(1998)p.328.
[34]D.K.Park and S.K.Yoo,Preprint arXiv:hep-th/9712134.
