有砟轨道下沉与高低不平顺关系分析
李凤煜,丁荣,许玉德
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804; 2.上海铁路局 上海铁路轨道交通开发有限公司 工程分公司,上海 200071)*
有砟轨道下沉与高低不平顺关系分析
李凤煜1,丁荣2,许玉德1
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804; 2.上海铁路局 上海铁路轨道交通开发有限公司 工程分公司,上海 200071)*
检验了六分之一模型的适用性,并对该模型进行修正,提出有砟轨道下沉与高低不平顺恶化关系的修正计算模型.得出六分之一模型能在一定程度上反映两者之间的关系,但当高低不平顺数据不服从正态分布或时间间隔跨度较小时,会出现偏离程度相对较大的情况;修正模型比六分之一模型的适用性更好,准确度更高.
现场实验;有砟轨道;轨道下沉;高低不平顺;关系模型
0 引言
轨道累积下沉是轨道高低不平顺发生、发展的直接原因,然而由于轨道下沉的复杂性和高低不平顺发展影响因素众多,致使两者之间的定量关系很难确定[1].国内外的研究机构和学者针对两者的关系都进行了许多研究,其中美国运输中心(TTC)、北美铁道协会(AAR)和英国铁路部门的研究指出,不平顺标准差与轨道下沉间存在线性关系[1];日本学者广井生马[2]、杉山德平[3]、内田雅夫[4]等先后提出了不平顺发展速率标准差为轨道下沉标准差的1.22倍、轨道下沉量与高低不平顺发展间关系式、高低不平顺标准差与轨道下沉量存在六分之一的关系模型;我国学者得到了采用轨道纵断面高程的标准差表示的轨道不平顺与轨道总下沉量之间的关系式,文献[5- 6]对式中参数进行了讨论.在各类文献资料与研究报告中,日本学者提出的六分之一模型应用最为广泛,然而该模型对于我国线路情况的适用性还有待进一步的研究.本文选取该模型作为基准模型,利用现场观测实验得到的轨道下沉量与高低不平顺标准差数据,对模型的适用性进行分析,并针对分析结果对其进行修正,以得到更适用于我国线路情况的修正模型.
1 现场实验
1.1 实验段的选取与测量计划
经过现场调查,最终将现场观测实验段选定在淮南线下行K28+876.47~ K29+236.23曲线处.该线路区间轨道结构具有一定的代表性,不含特殊扣件等特殊轨道结构,且该区间为客货混运,具备一定的运量条件,其主要货车车型为C64K、C70,轴重分别为21 t、23 t.
因为测量工作在捣固作业后进行更易得到下沉情况较为明显的分析数据,因此,测量工作选在实验段线路于2014年4~5月进行捣固作业后进行.于6月12日进行初始测量,7月31日及10月24日进行了第二、第三次沉降观测.同时,为了保证轨道高低不平顺数据与沉降观测数据的对应性,在现场条件允许的情况下,应尽量选择在沉降观测实验当天或附近的时间展开轨道高低不平顺的测量.故分别于6月12日,7月28日及10月21日进行了三次轨道高低不平顺的测量.
1.2 观测点与基准点布置
在现场实验段选取一段连续的120根轨枕范围区间,在每两根轨枕上布置轨道下沉的观测点,且在内外轨两侧的轨枕处均布置观测点,共计120个观测点.现场测点的布置示意图,如图1所示.
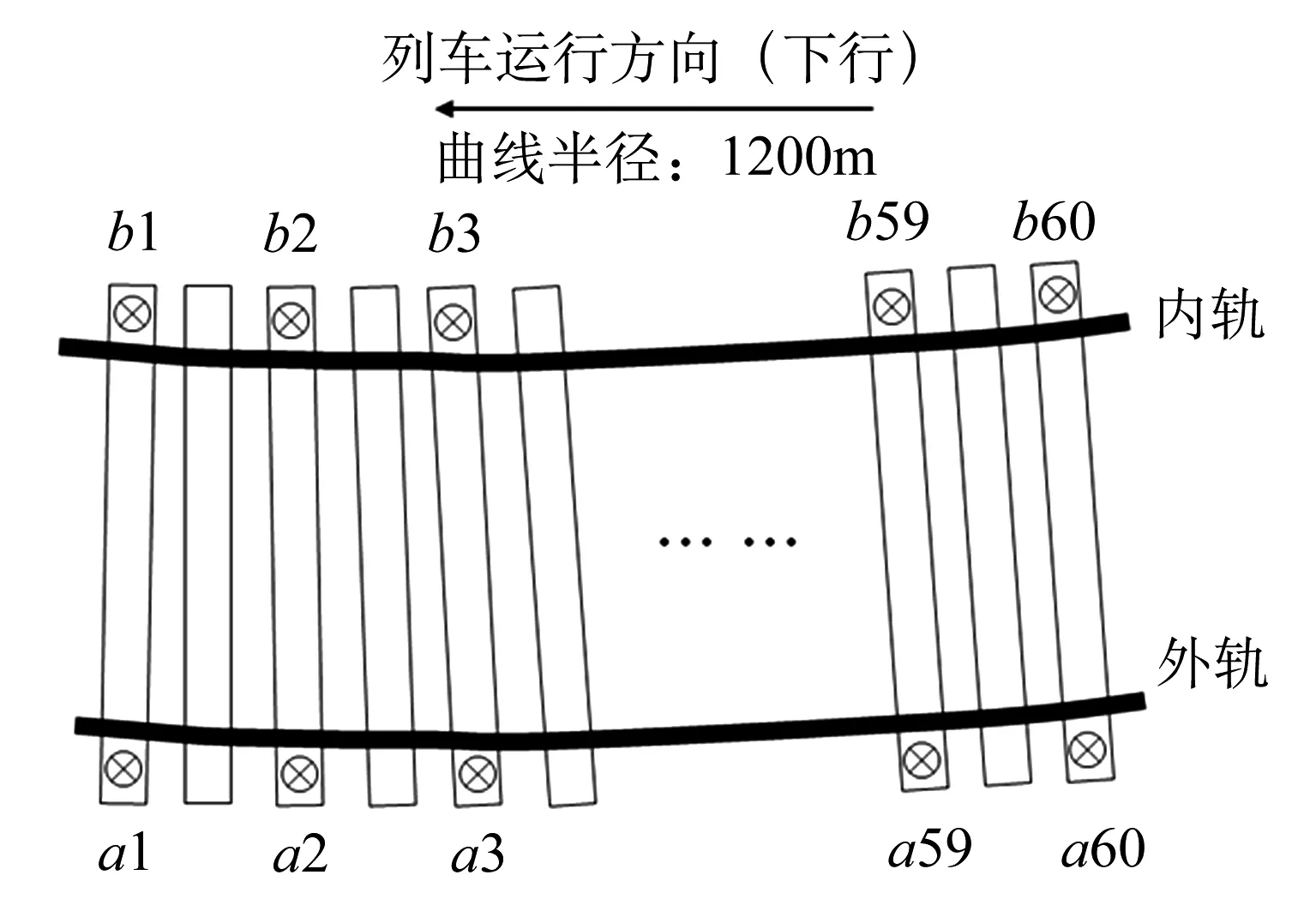
图1 现场测点布置示意图
1.3 轨道下沉数据
将相邻两次观测到的各观测点的相对高程的误差修正数据相减,即可得到各观测点在该时期内的高程变化量,即下沉量.由此可得7月28日相对于6月12日以及10月24日相对于7月28日的各观测点的下沉量.将两次的下沉数据相加,即可以得到10月24日相对于6月12日轨道各观测点的下沉量.将7月28日以及10月24日相对于6月12日的轨道各观测点的下沉量,按照外轨、内轨分别绘制于同一图像中,得到观测点下沉曲线图,如图2所示.
由图2可以发现,对于6月12日~10月24日这134天内,外轨各观测点的平均下沉量为-1.88 mm,最大下沉量为-8.78 mm(发生在a17点处),各点下沉量的标准偏差为2.02 mm;内轨各观测点的平均下沉量为-2.20 mm,最大下沉量为-8.62 mm(发生在b16点处),各点下沉量的标准偏差为2.40 mm.

(a)外轨

(b)内轨
1.4 高低不平顺数据
选取下行线现场实验区段的缓和曲线与圆曲线部分的轨道高低不平顺数据,即起始里程取在K28+876.47附近,结束里程取在K29+236.23,现场测量得到的轨道高低不平顺数据为每米两个点,即每0.5 m对应一个高低不平顺数据.将对应的三次轨道高低不平顺测量数据,绘制截取区段的轨道高低不平顺波形图,如图3所示.

(a)6月12日波形图 (b)7月28日波形图 (c)10月21波形图
图3 轨道高低不平顺
2 六分之一模型的适用性分析
2.1 正态分布检验
六分之一模型要求高低不平顺的数据基本服从正态分布规律,因此,在结合相关文献的基础上[7- 11],采用Jarque-Bera检验方法对现场实验测量得到的轨道高低不平顺数据进行正态分布拟合优度的检验.
以10月21日的高低不平顺数据为例,其正态概率图如图4所示,可以发现,对于左高低,正态概率图呈长尾分布,即可认为测量数据中较标准正态分布有更多偏离均值的数据;对于右高低,正态概率图呈短尾分布,即可认为测量数据中较标准正态分布有更多靠近均值的数据.取显著性水平α=0.05,Jarque-Bera检验的计算结果为左高低H=1,P=0.001 0,JB=35.554 1,CV=5.899 7;右高低H=0,P=0.122 5,JB=3.999 3,CV=5.899 7.对于左高低,由于H=1,P<0.05,且有JB>CV成立,故认为左高低在JB检验下不服从正态分布;对于右高低,由于H=0,P>0.05,且有JB (a)左高低 (b)右高低 同样地,可以对6月12日及7月28日的高低不平顺数据进行拟合优度检验,在此不再重复叙述. 将正态分布拟合优度检验结果汇总于表1中.由表中看出,对于三次轨道高低不平顺测量,右高低在Jarque-Bera检验下均服从正态分布,而左高低有一次服从正态分布,两次不服从正态分布.结合其正态概率图的形状以及相关文献资料,可以认为轨道高低不平顺基本接近于正态分布的规律,在条件较为严格的Jarque-Bera正态分布拟合优度检验下,仍能在大多数的情况下得到服从正态分布的结果,故可认为对该模型的这一假设是成立的. 表1 正态分布拟合优度检验 2.2 最大值与标准差数值关系检验 六分之一模型认为高低不平顺的最大值与标准差近似成3倍的关系.将高低不平顺的统计数据汇总于表2中,并计算其最大值与3倍标准差的关系. 表2 高低不平顺最大值与标准差的关系 由表2中数据可见,除6月12日与10月21日的左高低数据外,高低不平顺最大值与高低不平顺标准差近似满足3倍的关系,当高低不平顺数据在Jarque-Bera正态分布拟合优度检验下服从正态分布且拟合优度越高时,这样的关系越为明显;当高低不平顺数据在Jarque-Bera正态分布拟合优度检验下不服从正态分布时,这样的关系存在一定的偏离. 2.3 偏离程度检验 经上述分析可知,左高低数据普遍无法通过Jarque-Bera正态分布拟合优度检验,从统计学严格意义上,不接受服从正态分布的假设,故此处重点考察右高低数据,计算经过两次截取里程范围后的,局部区段高低不平顺的标准差,将计算结果汇总于表3中. 表3 高低不平顺标准差 (1) 验证6月12日~7月28日期间内的轨道下沉量与高低不平顺标准差的恶化关系: 计算高低不平顺标准差的发展值Δσ: Δσ实测=σ0728-σ0612=2.206-2.016=0.190 mm 由原始数据的统计结果可知,对应期间内所有观测点的轨道平均下沉量δ=0.81 mm,则: 与模型结论的偏离程度P可由下式计算: (2) 验证6月12日~10月21日期间内的轨道下沉量与高低不平顺标准差的恶化关系: 计算高低不平顺标准差的发展值Δσ: Δσ实测=σ0728-σ0612=2.337-2.016=0.321 mm 由原始数据的统计结果可知,对应期间内所有观测点的轨道平均下沉量δ=2.20 mm,则: 与模型结论的偏离程度P可由下式计算: 若取可接受的偏离程度为0.150[12],通过上述现场实验数据验证分析,可见6月12日~7月28日期间内的轨道下沉量与高低不平顺标准差的恶化关系与六分之一模型的结论偏离程度超过了0.150,故认为该模型对该期间的数据适用性不佳,计算结果的偏移量较大;6月12日~10月21日期间内的轨道下沉量与高低不平顺标准差的恶化关系与六分之一模型的结论偏离程度没有超过0.150,故认为该模型对该期间的数据适用性较好,计算结果的偏移量在可接受的范围内. 从上述计算结果来看,在两次计算中六分之一模型的偏离程度相差较大,其主要原因是6月12日~7月28日的时间间隔跨度相对较小,误差相对较大;而当把时间跨度取为6月12日~10月21日时,时间间隔跨度增大,模型的偏离程度也明显减小. 3.1 修正模型 根据对轨道下沉与高低不平顺恶化关系的现场实验数据验证结果可知,六分之一模型通过建立轨道下沉量与高低不平顺的标准差发展值之间的数值关系,能在一定程度上反映两者的恶化关系,对于不同的运营条件及轨道结构也具有一定的适用性,但当高低不平顺数据不服从正态分布或时间间隔跨度较小时,会出现偏离程度相对较大的情况. 因此,本文在六分之一模型的基础上,对其做了进一步的修正处理,以更好的适应现场测量数据的实际情况.保留六分之一模型的基本形式不变,引入线性偏移参数α,β对其进行修正,修正公式如下: 利用现场实验的实测数据对线性偏移参数α,β进行参数估计,计算得到: α=0.566, β=0.114 即有根据现场实验的恶化关系修正模型: 其中:Δσ为高低不平顺标准差的发展值;δ为轨道下沉量. 由于式(2)是根据淮南线典型实验区段数据得到的,故式(2)的恶化关系修正模型对该实验区段的适用性最好,同时也能适用于实验线上其他条件类似的区段,对于一些特殊的线路区段(特殊的轨道结构、路基/桥梁/隧道状态等)会存在一定的偏差. 3.2 偏离程度检验 (1) 验证6月12日~7月28日期间内的轨道下沉量与高低不平顺标准差的恶化关系: 由式2可以计算得到,高低不平顺标准差的发展值Δσ: 与模型结论的偏离程度P可由下式计算: (2) 验证6月12日~10月21日期间内的轨道下沉量与高低不平顺标准差的恶化关系: 由式(2)可以计算得到,高低不平顺标准差的发展值Δσ: 与模型结论的偏离程度P可由下式计算: 可以看出,修正后的恶化关系模型与六分之一模型计算得到的结果数量级相同,但修正模型对于淮南线典型实验区段的适用性更好,与六分之一模型相比准确度更高. 本文针对日本学者内田雅夫提出的高低不平顺标准差与轨道下沉量存在六分之一的关系模型,利用现场实验数据进行验证,得到以下结论: (1)六分之一模型能在一定程度上反映两者之间的关系,对于不同的运营条件及轨道结构也有一定的适用性,但当高低不平顺数据在Jarque-Bera正态分布拟合优度检验下不服从正态分布或实测数据的观测时间间隔跨度较小时,会出现偏离程度相对较大的情况; (2)利用六分之一模型和修正模型求高低不平顺标准差的发展值,得到的计算结果数量级相同,但修正模型比六分之一模型的适用性更好,准确度更高. [1]曾树谷.铁路散粒体道床[M].北京:中国铁道出版社,1997:245- 288. [2]佐藤吉彦.新轨道力学[M].北京:中国铁道出版社,2001. [3]杉山德平.軌道狂い進みの实态とその解析[R].鉄道技术研究报告,1978. [4]内田雅夫,石川達也,三和雅史.軌道狂い進みに着目した有道床軌道の新しい設計法[J].鉄道総研報告,1995,9(4):37- 42. [5]STEVEN,CHRISMER,ERNEST T,et al.Ballast fouling and drainage[J].Railway Track & Structures,1992(3):16- 17. [6]ZHANG YUJIANG,MURRAY MARTIN,FERREIRA LUIS.Effects of substructure on track performance,Track and transportation studies[C].Proc. of the Conference on Traffic and Transport Studies,ICTTS,1998:850- 859. [7]许玉德,李海峰,周宇.铁路轨道高低不平顺的预测方法[J].同济大学学报(自然科学版),2003(3):291- 295. [8]周宇,许玉德,李浩然.轨道不平顺非线性预测模型[J].交通运输工程学报,2004(4):21- 24. [9]马利衡,倪萍,梁青槐,等.沪宁城际铁路轨道高低不平顺状态分析[J].北京交通大学学报,2014(3):50- 54. [10]何永春,王午生.铁路轨道高低不平顺的预测及其应用[J].上海铁道大学学报,1999(2):64- 70. [11]高建敏.基于状态转移概率矩阵的轨道不平顺发展预测研究[J].铁道建筑,2011(7):140- 143. [12]高建敏,翟婉明,徐涌,等.基于概率分布的轨道不平顺发展统计预测[J].铁道科学与工程学报,2006(6):55- 60. Analysis and Study of Relationship between Ballasted Track Settlement and Track Vertical Profile Irregularity based on Field Experiment LI Fengyu1,DING Rong2,XU Yude1 (1.Key Laboratory of Road and Traffic Engineering of Ministry of Education,Tongji University,Shanghai 201804,China; 2.Shanghai Railway Bureau,Shanghai 200071,China) The applicability of the one-sixth model is verified and modified.A modified model of the relationship between settlement of ballasted track and deterioration of track vertical profile irregularity is proposed. The conclusions are that the one-sixth model can reflect the relationship between the two in a certain extent, but the degree of deviation is relatively large when the irregularity data doesn’t obey the normal distribution or the time interval is short, the modified model has better applicability and higher accuracy than the one-sixth model. field experiment; ballasted track; track settlement; vertical profile irregularity; model of relationship 1673- 9590(2017)01- 0094- 05 2016- 05- 10 李凤煜(1993-),女,硕士研究生,主要从事轨道工务方面的研究 E-mail:fengyu_lee@163.com. A





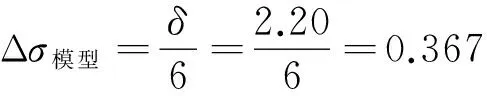
3 恶化关系模型的修正
4 结论

