铁路物流中心选址-分配问题研究
吴醒,宋瑞,靳国伟
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044)*
铁路物流中心选址-分配问题研究
吴醒,宋瑞,靳国伟
(北京交通大学 城市交通复杂系统理论与技术教育部重点实验室,北京 100044)*
为了满足铁路集中化运输的要求,基于铁路物流中心的层级特点,结合分层选址的理论和方法,以铁路物流中心覆盖的总需求最大化和物流运输成本最小为目标,以各级物流中心数量、服务能力和服务覆盖范围为约束,构建了铁路物流中心分层选址-分配的0- 1整数规划模型.最后针对铁路物流中心选址-分配模型的特点,设计了算例,并采用ILOG CPLEX软件进行求解.算例结果验证了该选址-分配方法的有效性和可行性.
铁路运输;选址-分配;铁路物流中心;分层覆盖;ILOG CPLEX
0 引言
进入21世纪,随着IT技术、互联网和通讯技术的广泛应用,物流在社会经济发展中的地位越来越重要.而在物流体系中,物流配送中心的地位格外突出.铁路运输具有比其他运输方式的优势,铁路运输比公路运输运量大,比航空运输运费低,而且铁路运输安全可靠.由于铁路物流客户众多、区域广泛、线路过长、业务量较大的特点,单个铁路物流配送中心无法按时高效执行配送业务,应该考虑建立多级、多层次的网络和物流配送中心体系或者两级网络和配送中心体系.
目前,国内外对铁路枢纽物流中心选址已进行了系列研究.在国内,冯文成[2]分析铁路枢纽物流中心站选址影响因素,引入集对-熵权理论分析模型.纪寿文[3]从供给、需求两方面研究铁路物流中心的中观选址问题,建立包括配送费用、铁路作业费用、中转费用的总费用最小的“备选点-货源地”的两层规划模型,但并未综合考虑分级选址.陈强[4]在枢纽选址模型中,将服务频率作为决策变量,在迭代过程中采用极大邻域搜索算法进行求解,最后在服务频率不变的情况下确定综合货运网络的枢纽及枢纽间不同运输方式的流量分配.魏延青[5]根据受灾区域的受灾程度进行了分层,并以救灾物资需求满意度为目标建立了最大问题覆盖选址模型.郑斌和马祖军[6]以震后恢复期为背景,构建了“集散点—物资配送中心—受灾点”的两级物资配送网络系统,并设计了一种结合启发式规则的分周期、分阶段解码的混合遗传算法对该问题进行了求解.在国外,Sahin和Süral[7]根据流动模式、服务多样性、空间结构和目标对分层结构进行了分类.Serra[8]考虑了一个具有两级设施的连贯选址模型.这是一个双目标模型,对于较低级别设施具有距离最小化目标函数而对于较高级别设施使用最大覆盖准则.在Marianov 和 Serra[9]的论文中,为单流,无嵌套和非连贯系统提出覆盖模型.Lee[10]提出基于部分覆盖的分层覆盖选址模型.Vladimir和Daniel[11]为连贯的分层系统提出了最大覆盖模型.
本文考虑目前最常见的两级物流中心网络,分别为全国性综合铁路物流中心和地区性铁路物流中心.基于铁路物流中心分层的特点,结合设施选址方法,建立了一个以覆盖的总需求最大为目标的分层覆盖选址-分配模型,该模型是一种离散点选址模型,并采用ILOG CPLEX对模型进行了求解.
1 铁路枢纽物流中心选址数学模型
1.1 问题描述
物流中心选址是在一定经济区域中进行,该经济区域内要具有若干供应点和足够的货运量需求.目前物流中心选址主要有分层和不分层选址两种,其中后者适合公路运输,而一般不适合铁路运输,这是由铁路运输的集中化运输组织方式决定.在铁路运输中采用双重整合策略,货物装车组成车组,再由车组组成车列.铁路物流中心选址,即为各级别铁路物流中心选择最优的节点,同时考虑运输部门和需求单位两方的利益,用最小的运输成本来满足需求节点最大的物流需求量.目标选择区域是一个离散的候选位置的集合,候选位置的数量有限,候选点的服务范围也有限.另外,各级别物流中心服务的最大能力不同,在规划选址时应考虑物流中心建成后承担的需求节点的物流运输需求均在物流中心各层次服务的最大能力范围内,并且满足的物流节点总需求量至少达到一定值以避免资源浪费.基于铁路运输组织的特点和铁路物流中心的分级特点,本文拟采用分层选址的思想,实现各级中心的一体化选址.为了简化实际问题便于建立模型进行求解,模型的构建基于以下假设:①铁路物流中心是分层的;②各级物流中心是非嵌套的,即各级物流中心提供不同的功能;③物流服务是连续的,即到达最低级别物流中心的物流需求最终都要分配给最高全国性的物流中心,如图1所示;④物流运输成本与运输距离成正比;⑤结合各级铁路物流中心运行的实际情况,假设全国性综合铁路物流中心的覆盖距离为200 km,地区性铁路物流中心的覆盖距离为60 km,假设全国性综合铁路物流中心的服务能力都为2 000 t,运输成本为13元/km.

图1 铁路物流中心选址-分配图
1.2 变量定义
设I为需求点集合,i∈I;J为地区性铁路物流中心集合,j∈J;K为全国性综合铁路物流中心集合,k∈K.ai表示需求节点i的物流需求量;dij表示需求节点i到地区性铁路物流中心j的距离;ejk表示地区性铁路物流中心j到全国性综合铁路物流中心k的距离;Ej表示地区性铁路物流中心j的最大能力;Ek表示全国性综合铁路物流中心k的最大能力;c为每公里的运输成本;p为地区性铁路物流中心的数量上限,为给定值;q为全国性综合铁路物流中心的数量上限,为给定值;m为地区性铁路物流中心的服务覆盖范围上限,为给定值;n为全国性铁路物流中心的服务覆盖范围上限,为给定值;t为需求节点总需求量至少要满足的百分比,为给定值.
决策变量有以下四个:xijk为0- 1分配决策变量,如果需求节点i的物流量全部分配给1个地区性铁路物流中心j,然后再分配给1个全国性综合铁路物流中心k,则为1,否则为0;yjk为0- 1变量,如果分配给地区性铁路物流中心j的需求全部分配给全国性综合铁路物流中心k则为1,否则为0;wj为0- 1选址决策变量,如果地区性铁路物流中心选在节点j则为1,否则为0;zk为0- 1选址决策变量,如果全国性综合铁路物流中心选在节点k则为1,否则为0.
1.3 建立模型
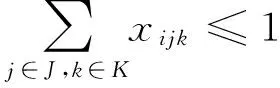








xijk,yjk,wj,zk∈{0,1},∀
其中:式(1)和式(2)为目标函数,式(1)表示使覆盖物流节点的需求最大化,式(2)表示使总的运输成本最小.式(3)~式(15)为约束条件.式(3)确保每个需求节点i的所有物流量分配给至多每个级别的一个物流中心.式(4)和(5)确保所有分配给低一级物流中心的需求至多分配给同一个高一级的物流中心.式(6)和(7)保证除非在j、k建立相应级别的物流中心,否则这些级别的节点不会联系起来.式(8)和(9)是各个级别建立的物流中心数量的上限.式(10)和(11)确保到达每个物流中心的物流量不超过其服务能力.式(12)确保满足的物流节点总需求量达到的最小值.式(13)和(14)确保到达各级别物流中心的服务网点不超过其服务覆盖范围.式(15)为决策变量约束,都为0- 1变量约束.
2 模型求解
2.1 多目标模型求解方法
上述模型是一个0- 1整数规划模型,包含较多的变量和约束条件,该模型可以采用CPLEX优化软件求解.ILOG CPLEX是IBM公司中的一个优化引擎.ILOG CPLEX 能够以最快的速度最可靠地实现基本算法,以解决困难的数学优化问题.CPLEX提供灵活的高性能优化程序,解决线性规划、二次方程规划、二次方程约束规划和混合整型规划问题.
多目标优化方法是将多目标优化问题中的各个分目标函数经处理和数学变换聚合成一个单目标函数,然后采用单目标优化方法进行求解.本文采用如下步骤对多目标进行处理[12]:
(1)分别求解目标函数Z3(-Z1,将最大化问题转化成最小化问题便于后面求解)和Z2来构建理想解的收益表,如表1所示.理想解实现了每个目标函数的同时优化.表1中,x是求得的最好折衷解.对于目标函数Z3,x3*是最优解,U3和L3分别是解集的上下界;而对于目标函数Z2,x2*是最优解,U2和L2分别是解集的上下界.
表1 理想解的收益表

Z3(x)Z2(x)xMinZ3Z3(x3*)Z2(x3*)x3*MinZ2Z3(x2*)Z2(x2*)x2*U3=maxZ3(x3*),Z3(x2*)U2=maxZ2(x3*),Z2(x2*)L3=minZ3(x3*),Z3(x2*)L2=minZ2(x3*),Z2(x2*)
(2)构建目标函数Z3和Z2的隶属函数μ3(x)和μ2(x),如下式:
(3)通过聚集μ3(x)和μ2(x),使用扩充最大最小算子,获得单目标规划模型,如下:

目标函数(1)~(2),约束(3)~(15)
其中:α是折衷的总体满意水平(最大化),ε是一个小的正数.因为在式(18)中,μ3(x)和μ2(x)的平均算子是完全代偿的,所以当α最大时会产生一个非支配解.然后采用ILOG CPLEX求解此转化的单目标规划模型.
2.2 应用ILOG CPLEX的算例分析
为了验证模型的有效性,设计了如下算例.假定某一区域内,含有10个全国性综合铁路物流中心候选点,20个地区性铁路物流中心候选点和100个需求节点.本算例中设计允许建造不超过5个全国性综合铁路物流中心和10个地区性铁路物流中心.不同等级城市对应不同的需求节点,各自的物流需求量有所差别,本例中17号需求节点需求量最大,为99 t;93号需求节点需求量最大,为5 t,平均物流节点需求量为56.76 t.给定20个地区性物流中心候选点的服务能力,3号候选点最大分别为700 t,4号候选点最小为256 t,平均候选点服务能力为483.2 t.给定全国性综合铁路物流中心候选点的服务能力相同,都为2 000 t.运输成本为13元/km.表2和表3分别给出了需求节点和地区性铁路物流中心之间的距离矩阵、地区性铁路物流中心和全国性综合铁路物流中心之间的距离矩阵.由于表格篇幅较大,在此只列出部分数据.为避免资源浪费,最少需满足所有物流需求节点总需求量的65%.

表2 需求节点到地区性铁路物流中心候选点的距离 km
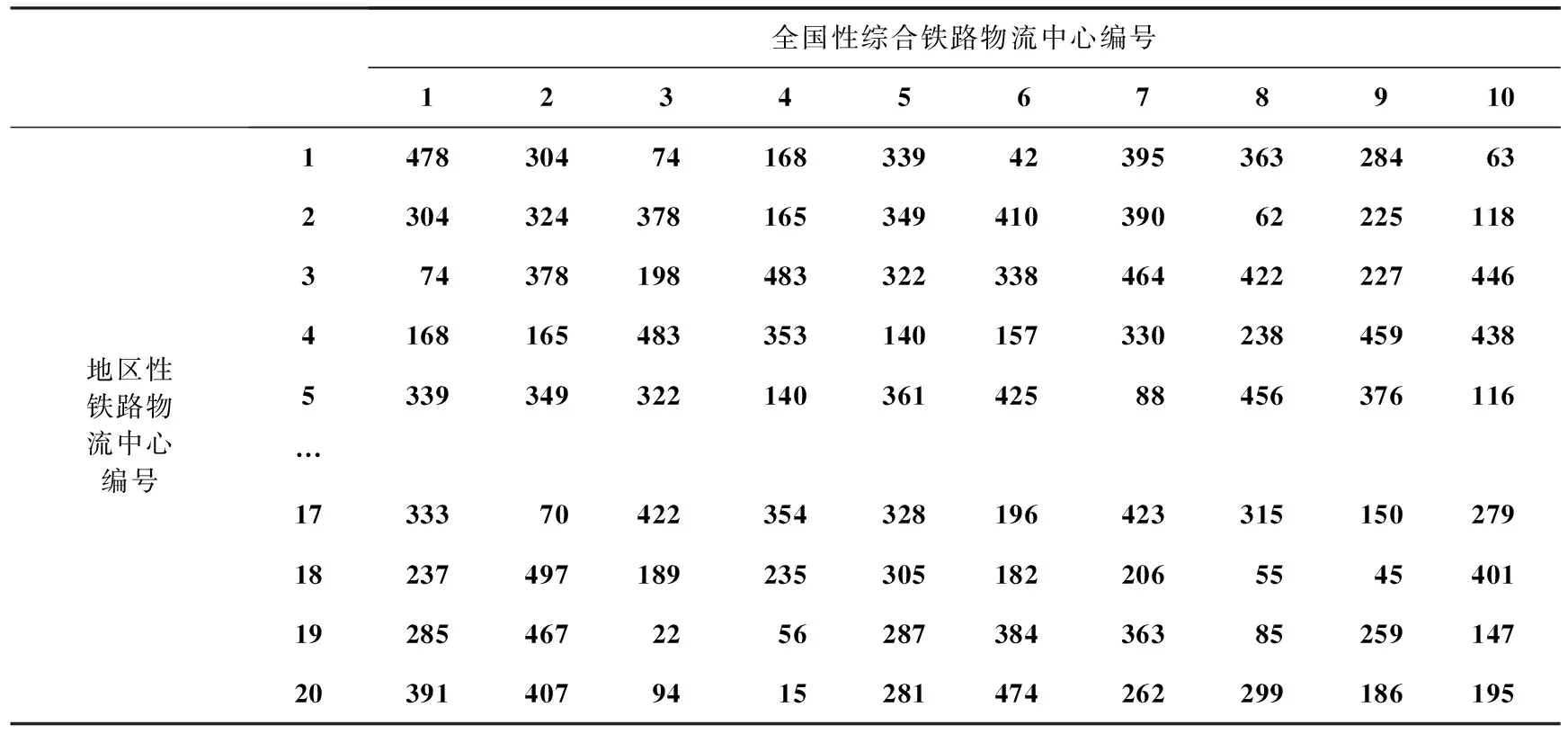
表3 地区性铁路物流中心候选点到全国性综合铁路物流中心候选点的距离 km
2.3 结果分析
在Intel(R) Core(TM) i5 CPU @ 1.60 GHz,8.00 GB内存,Windows8操作系统环境下,将数学模型和基础数据等编成ILOG CPLEX软件语言,写入软件对模型进行求解.先分别对单目标进行求解,再利用3.1节中的方法对双目标进行求解,用时均在5 s以内,最终对比结果如表4所示.分析可知,只考虑最大化覆盖物流节点需求导致运输成本提高119.1%,而只考虑最小化物流运输成本又会导致覆盖的物流节点需求减少12.7%;双目标情况下,选址方案的需求满足率为78%(所有需求节点的总物流运输需求为5 176 t),兼顾了覆盖需求和运输成本两个方面,物流中心的选址方案更为合理.

表4 单双目标下选址方案对比结果
3 结论
有别于依托公路的物流中心选址,铁路物流中心选址具有一定的独特性.本文针对铁路物流中心选址问题进行研究,根据铁路物流中心的层级特点,结合有限物流中心候选点的服务能力、服务范围,以覆盖物流需求节点最大和物流运输成本最小为优化目标,构建了铁路物流中心一体化选址模型,并设计了较大规模的算例,使用软件ILOG CPLEX对模型进行了求解,结果表明,在有限的物流中心候选点的服务覆盖范围和服务能力内能够最大化地满足物流需求节点的需求量,并且即使问题规模较大也可以被高效解决.该选址-分配方法考虑了影响物流中心候选点选址的各种因素,目标兼顾供给方和需求方两方利益,使其更加符合实际情况,对于更多层次的物流中心选址-分配具有参考价值.
[1]单宝伟. 基于物流量预测的铁路物流中心规划研究[D].兰州:兰州交通大学,2012.
[2]冯文成,曲思源. 基于集对-熵权分析的铁路枢纽物流中心站选址的研究[J].铁道经济研究,2013(2):89- 92.
[3]纪寿文,黄婷婷. 混合整数规划的铁路物流中心选址建模求解[J].铁道运输与经济,2011,33(9):62- 65.
[4]陈强. 基于VLSN算法的综合货物运输网络枢纽选址及服务频率确定研究[D].北京:北京交通大学,2009.
[5]魏延青,徐庆,荣亚军,等. 基于救灾物资满意度的最大覆盖选址问题[J].物流工程与管理,2013,35(1):50- 53.
[6]郑斌,马祖军. 震后恢复期物资配送中的多周期选址—联运问题[J].交通运输系统工程与信息,2014(4):230- 238.
[7]SAHIN G, SÜRAL H. A review of hierarchical facility location models[J]. Computers & Operations Research, 2007, 34(8):2310- 2331.
[8]SERRA D. The coherent covering location problem[J]. Papers in Regional Science, 1996, 75(1):79- 101.
[9]MARIANOV V, SERRA D. Hierarchical location-allocation models for congested systems[J]. European Journal of Operational Research, 2001, 135(1):195- 208.
[10]LEE J M, LEE Y H. Tabu based heuristics for the generalized hierarchical covering location problem[J]. Computers & Industrial Engineering, 2010, 58(4):638- 645.
[11]MARIANOV V, SERRA D. Hierarchical location-allocation models for congested systems[J]. European Journal of Operational Research, 2001, 135(1):195- 208.
[12]CHANG Y H, YEH C H, SHEN C C. A multiobjective model for passenger train services planning: application to Taiwan's high-speed rail line[J]. Transportation Research Part B Methodological, 2000, 34(2):91- 106.
Problem Study of Location-Allocation for Railway Logistics Center
WU Xing,SONG Rui,JIN Guowei
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology,Beijing Jiaotong University,Beijing 100044,China)
To meet the demand of railway integration transportation,a hierarchical location allocation model which maximizes the total covering needs of the railway logistics center and and minimizes the transport costs is proposed based on the hierarchical characteristic of railway logistics center, combining with the theory and methods of hierarchical location under the consideration of the constraint that the number, service ability and service coverage of railway logistics center is limited. Finally, according to the characteristics of railway logistics center location allocation model, an example is given, and ILOG CPLEX software is used to solve it. Results of the example show that the location-allocation method is effective and feasible.
railway transportation; location-allocation; railway logistics center; hierarchical covering; ILOG CPLEX
1673- 9590(2017)01- 0007- 05
2016- 04- 09
国家自然科学基金资助项目(61374202);中国铁路总公司科技研究开发计划资助项目(2013X005-A、2014X009-H)
吴醒(1993-),男,硕士研究生;宋瑞(1971-),女,教授,博士,主要从事运输组织理论与技术的研究
E-mail:14120903@bjtu.edu.cn.
A

