高中物理解题中极限思维法的应用

张 翔

(山东省潍坊市安丘一中 262100)

高中物理中有很多复杂的知识概念，解题难度也很大，所以我们平时在学习物理时都会感到吃力，打击了我们学习物理的信心，很多同学对物理学习也不感兴趣，让我们的物理综合能力不高，面对高考的考查，我们更需要改变这一现状，提高解题水平和能力.这就需要我们掌握极限思维，通过这一方法进行解题，可以让我们的解题思路得到拓展，提高我们的解题效率及质量，提高我们的物理学习效果.

一、高中物理解题中极限思维法的重要性

该方法在物理解题中进行应用，解题思路就是在解题过程中，将题目中已知的某个空间内变化关系的两个变量表现成单调下降或者是上升的函数关系，进而在解题中，将其中的一个变量假设成值升到区间的极点，解决问题.在实际使用极限思维方法时，可以根据已知经验和实施作为基础，利用这一方法让题目中的主观问题和因素体现出来，进而让我们更好的理解题目，找到解题思路和答案.

我们在使用这一方法解物理题目时，重点就是对于题目中变量和条件的定位，对持续变动的量赋予极值，让其可以显现出的单一、简单的特征.我们在解物理题时使用这一方法，可以有效提升我们解难题的效率，还可以促进我们解题思路的发展，实现更快、更好的解题，促进我们物理综合能力的提升.

二、高中物理解题中极限思维法的应用

1.寻找解题突破口

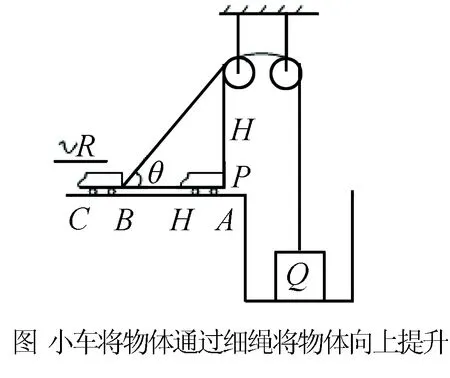
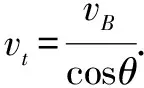
2.提高解题效率

在高中物理解题中使用极限思维方法可以有效提高我们解题的效率，比如在解题：“装置处于平衡状态，若是将AC换作一条相对长一些的绳子，AC＇、AB杆位置竖直状态，此装置还是可以保持平衡，则AC＇，长绳承受的张力T与AB杆承受到的压力N这两者同原来的对比，是( )？有四个选项，分别是：A(T增大，N减少),B(T与N都增大),C(T减小，N增大),D(T,N都减小)”，在解这道题目时，我们会使用常用方法解读题目，会设AC长绳和水平方向存在的夹角是θ，然后把A当成研究对象.A受到三种力共同作用，其保持平衡状态，分别是AB杆的支持力N＇、AC长绳的拉力T＇以及AD绳拉力.在这里，AD绳拉力和G是一样的，根据共同点平衡条件，可以建立方程：竖直方向:N＇-T＇sin=0，水平方向:G-T＇cos=0.根据牛顿第三定律可以知道T＇=-T，N＇=-N，进而求出二者的大小是：T=G/cosθ及N=Gtgθ.从这两个式子中可以知道，随着θ的减少T和N也在减小，因此可以得出答案是D，用这样常规的方法进行解题，速度较慢，在考试中浪费时间，考试时间是有限的，因此要提升解题效率，就可以使用极限思维方法，当θ是0°是，得出N=O,T=G.当θ为90°时，N＇很多，因为T和N是相等的，所有二者同样很大，在角变小时，二者也会同样变小，进而可以很快的求解出答案.

3.运用极限思维法检验解题结果

综上所述，极限思维方法在高中物理解题时应用，可以帮助我们拓宽思路，提高解题效率，还可以验证解题结果，提高我们解题的正确率，因此，我们需要掌握好这一方法.

[1]周志宏.极限思维法在高中物理解题中的应用[J].高等函授学报(自然科学版),2012(06).

[2]潘玉楼.浅谈直觉思维在高中物理解题中的应用[J].读与写(教育教学刊),2012(07).