辨析几何概型中基本事件的选取角度

黄光鑫

(四川师大附中 610066)

学生在解答某些几何概型问题时，有时会因为思考的角度不对导致解题出错.请看下面两个问题.

例1 如图1所示，在等腰直角△ABC中，过直角顶点C在∠ACB内任作一条射线CM，与直线AB交于点M， 求AM小于AC的概率.

例2 如图2所示，在等腰直角△ABC中，在斜边AB上任取一点M，求AM小于AC的概率.

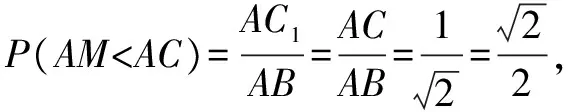
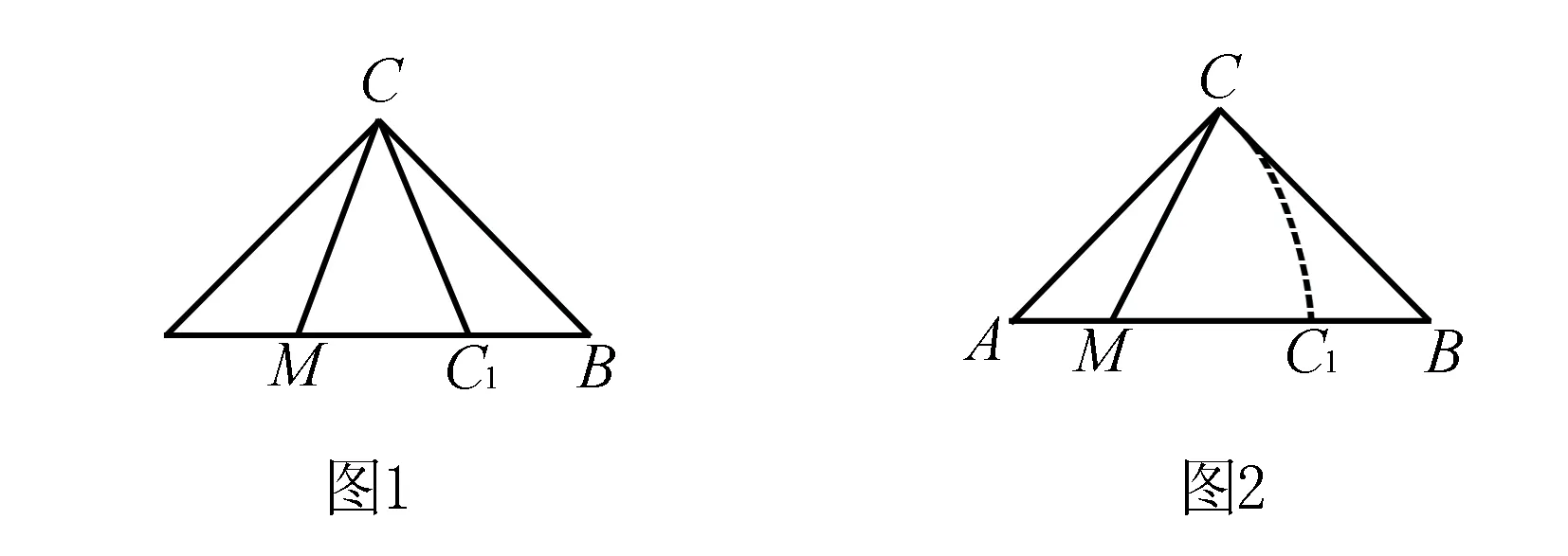
辨析从第(1)小题的叙述可知，射线CM是在直角∠ACB的内部区域等可能的出现.

从第(2)小题的叙述可知，点M是在线段AB上等可能的出现.对于第(2)问学生没有疑问.对于第(1)问，不少学生都搞不清楚为什么不是长度之比？关于这个问题我们从数学和物理两个方面进行分析.

从数学的角度看，当CM转动相同的角度如图3，∠ACM=∠MCM1时，在AB上产生的线段AM与MM1是否相等.连接MD，易知△ACM≌△DCM，显然∠CM1B>∠CAB，∠CM1B=∠MM1D,∠CAB=∠M1DM,∴∠MM1D>∠M1DM，从而MD>MM1.

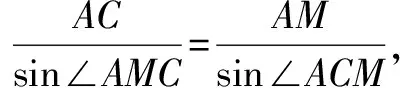
综上所述，第(1)小题的概率应该是角度之比而不是长度之比.所以对于背景相似的问题，当等可能的角度不同时，其概率是不一样的.这就要求我们求解几何概型问题时，一定要准确理解题意，弄清实验的基本事件是什么，且保证基本事件是等可能发生的，正确选取思考问题的角度.

[1]杜志建.中学教材学习讲义高中数学必修3[Z]. 乌鲁木齐：新疆青少年出版社 ，2012第1版.