剥离温度影响的锚杆轴力监测成果分析

许景春，俞俊平，武立军，杨再任

(1.赣州高速公路有限责任公司，江西 赣州 334100；2.江西省交通科学研究院，南昌 330200；3.中铁隧道勘测设计院有限公司，天津 300133；4.贵州省水利水电勘测设计研究院，贵阳 550002)



剥离温度影响的锚杆轴力监测成果分析

许景春1，俞俊平2，武立军3，杨再任4

(1.赣州高速公路有限责任公司，江西 赣州 334100；2.江西省交通科学研究院，南昌 330200；3.中铁隧道勘测设计院有限公司，天津 300133；4.贵州省水利水电勘测设计研究院，贵阳 550002)

锚杆支护加固效果评价常依赖锚杆轴力的监测，但边坡中影响锚杆轴力的因素众多，故分析锚杆轴力的成因具有重要的意义。借助某高速公路超高岩质边坡的锚杆轴力监测，定性分析影响锚杆轴力大小的因素，然后针对各因素定量化，建立锚杆轴力多元线性回归模型，进而剥离温度影响，计算所受边坡变形影响的真实轴力，准确评价锚杆的加固效果，降低对边坡变形破坏的误判。将本方法成功应用于锚杆MGZ1042测点真实轴力的计算，通过剥离温度影响，锚杆轴力由原来的100 kN降至真实轴力40 kN，未超过锚杆轴力监测警戒值60 kN，从而正确判断了边坡变形破坏趋势。

岩质边坡；锚杆轴力；监测；温度影响；回归模型

1 研究背景

路堑岩质高边坡爆破和开挖易导致岩体的卸荷回弹及局部的变形失稳，工程中常用锚杆(索)对岩质高边坡进行加固。为了了解其加固效果及边坡稳定性，需对锚杆(索)进行轴力监测。由于影响锚杆轴力的因素众多，前人对锚杆轴力进行了深入的研究[1-3]：王发玲等对锚杆支护机制受力形式进行了分析研究[4-5]，朱焕春详细分析了锚杆应力的边坡开挖效应、温度效应和时效变形效应[6]，徐卫军、黄清保等定性描述了锚杆应力随着边坡开挖的变化过程曲线及其相关性[7-8]。针对影响锚杆应力的因素，刘祖强、李宏恩等对边坡锚杆应力进行了定量分析并建立了相应的锚杆应力回归模型[9-10]。陈志坚等对影响锚杆应力的主要因素温度进行分析研究，引入虚拟温度场，提出剥离温度影响锚杆应力的方法[11]。以上研究侧重锚杆应力单方面的研究，且很少剥离温度的影响，即使有也只是提出剥离的方法，未对其开展进一步的研究。

本文结合上述文献，借助某高速公路超高岩质边坡锚杆轴力监测，建立锚杆轴力的多元线性回归模型，并对其进行温度因子的剥离，还原锚杆对边坡作用的真实轴力, 准确评价锚杆的加固效果。

2 工程概况

某高速公路采用明挖方式横穿中云台山，从而在高速公路两侧形成高陡岩质路堑边坡。研究的对象边坡最大坡高超过200 m，属一级边坡工程。边坡分20级开挖，每级坡高10 m，单级坡角55°，总体坡角为43°，采用喷锚支护。为保证施工及运营期的安全，该边坡布置有多点位移计、微压传感器、渗透压力计、锚杆应力计、防护网应力计、竖直测斜等监测仪器。边坡所用锚杆长8 m，采用A25螺纹钢筋，应力监测传感器安装于坡内5.5 m深处，共布置了72个测点。边坡总体形态及锚杆应力计布置如图1所示。

图1 锚杆测点立面布置

3 锚杆受力状态及影响因素分析

为了追踪锚杆加固效果和边坡稳定性的发展趋势，对边坡不同位置的锚杆进行轴力监测。部分测点的锚杆轴力监测结果特征如表1所示。

表1 部分测点的锚杆轴力变化特征

由表1监测结果可知：绝大多数锚杆轴力都在-10～10 kN范围内变化，少数监测点MGZ1242，MGZ1143，MGZ1042锚杆轴力较大，均出现在边坡西南侧，这是由于临近废弃采石场，岩体破碎松动，且采用非控制大爆破开挖，加剧岩体的变形，导致南侧锚杆轴力远大于北侧，其中MGZ1042最大值达到100 kN。锚杆轴力主要呈波动式变化，呈受拉状态，有些锚杆轴力增长但后期趋于平稳，表明除了局部地区外，边坡还是较稳定的。锚杆轴力变化趋势的不一，且局部地区轴力较大，因此有必要对锚杆轴力受力成因及变化过程作进一步的研究。

3.1 影响锚杆轴力的因素

锚杆轴力的实测结果主要受3种因素的影响：温度、边坡开挖及岩体时效变形。

3.1.1 温度对锚杆轴力影响的分析

锚杆轴力变化趋势呈波动形式都与温度具有一定的相关性，从上述表中发现绝大多数的锚杆轴力波动与温度呈负相关性，少部分锚杆轴力波动与温度呈正相关性。如图2中的(a)，(b)所示，MGZ1342，MGZ742测点的锚杆轴力与温度呈负相关，即温度上升，锚杆轴力减小，温度下降，锚杆轴力增大。究其原因是由于钢筋与岩体、砂浆线胀系数差异导致的，锚固体中钢筋、岩体、黏结砂浆相互作用，当温度升高时三者均发生膨胀，反之则发生收缩。根据文献[11]所列出的线胀系数钢筋为(12～13)×10-6/℃，混凝土为10×10-6/℃，花岗岩为7.9×10-6/℃，板岩为10.4×10-6/℃，石灰岩为8×10-6/℃，由此可知，锚杆线胀系数最大。当温度发生变化时，为了坡内各种介质变形的相互协调，锚杆变形受到周围砂浆的限制表现为受压或者受拉，正好呈负相关。温度下降锚杆收缩受到约束而产生拉应力，表现为轴力的增大；反之同理。

如图2(c)，MGZ845测点的锚杆轴力与温度呈正相关，即温度升高，锚杆轴力增大，温度降低，锚杆轴力减小，和上述理论完全矛盾。造成此种现象有可能存在2种原因：①岩体破碎，温度的变化波动时锚杆的变形不大于岩体的变形，使得锚杆变形不再受周围砂浆、岩体的约束；②砂浆质量较差或者锚杆灌浆饱和度不够，或者岩体的破碎导致漏浆，即使是岩体变形随温度变化比锚杆小，由于锚杆周围的介质起不到对锚杆约束作用[6]。结合MGZ845所处的地质环境，正好处在边坡西南侧，该处岩体破碎，可知轴力变化是原因一所致。

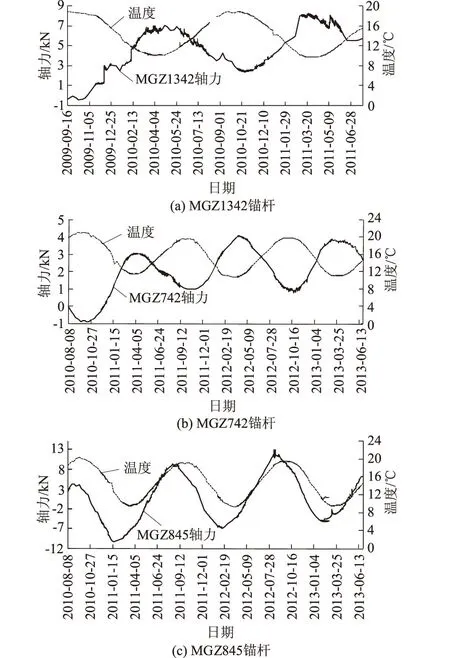
图2 MGZ1342,MGZ742,MG2845锚杆轴力与温度关系曲线

3.1.2 边坡开挖对锚杆轴力影响的分析

如图3中的(a)，(b)锚杆轴力随边坡开挖变化曲线可知： 124～54 m高程中每级台阶的开挖，锚杆轴力均发生或大或小的突变，呈“阶梯状”变化； 114台阶的开挖引起MGZ1342锚杆轴力变化了1.8 kN，MGZ1344变化了2.2 kN；104台阶的开挖引起MGZ1342锚杆轴力变化了1.6 kN，MGZ1344变化了1.5 kN。对比不同台阶开挖对锚杆轴力的影响可知：开挖台阶离测点越近，对测点锚杆轴力影响越大，反之，离测点越远，对锚杆轴力影响越小边坡开挖54 m高程以下的台阶对锚杆轴力几乎没有影响。锚杆轴力呈“阶梯状”变化侧面证明锚杆对开挖引起岩体变形锚固效果明显，有效控制了岩体的变形，增强了边坡整体与局部的稳定性。边坡开挖引起锚杆轴力变化一般是不可逆的。

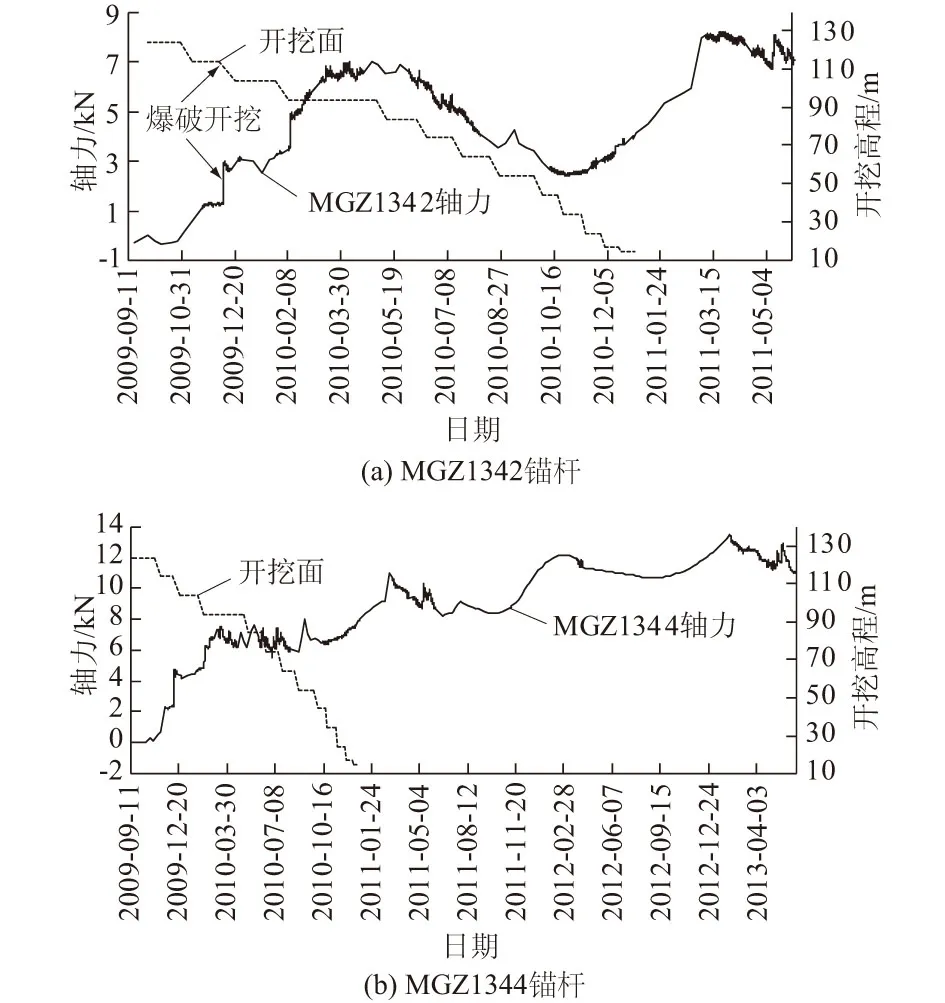
图3 MGZ1342,MG21344锚杆轴力随 边坡开挖变化曲线

3.1.3 时效变形对锚杆轴力影响的分析

图3中的(a)，(b)均表现出时效变形对锚杆轴力的影响。图3(a)中MGZ1342锚杆轴力除了呈现“阶梯式”变化和波动变化外，随着时间推移，当年轴力波动的峰值大于前年，具有螺旋式的上升趋势。图3(b)中MGZ1344锚杆轴力受时效变形影响更为明显，开挖结束之后锚杆轴力持续增大，后期也呈现出锚杆轴力的衰减，从开挖结束到锚杆轴力趋于稳定经历了近2.5 a的时间，有些部位的锚杆轴力稳定只要0.5 a或者1 a时间，说明边坡不同部位的时效变形效果不一，所以对边坡的安全监测是一个长期过程，基于长期和实时的监测才能准确评价边坡稳定性及加固效果。根据表1统计的各测点锚杆轴力变化趋势可知，轴力的波动式上升或衰减、持续的上升或衰减均有时效变形的影响，最后各个测点的轴力都趋向于稳定。 这说明大部分测点锚杆轴力时效变形不明显，坡面变形较小，且少有持续性的时效变形，该岩质高边坡是较稳定的。

表1中76%测点锚杆轴力随温度呈波动变化，锚杆轴力主要受温度因素影响，其他因素次之。但温度引起锚杆轴力波动变化对判断边坡的变形破坏用处不大，反而是开挖、降雨及时效变形导致的轴力变化值得研究，因为这3种因素对边坡的变形影响是不可逆的，容易导致边坡的变形破坏。由于锚杆轴力受周围温度影响而不受边坡变形影响，故通过锚杆轴力大小判断边坡变形破坏可能造成误判。所以本文提出建立锚杆轴力统计模型，剥离温度影响，计算真实轴力是很有必要的。

4 建立锚杆轴力影响因素统计模型

前文着重分析了锚杆轴力的变化过程及其影响因素，且各影响因素与轴力都呈正相关或负相关，此为定量分析各因素对锚杆轴力影响的大小创造了先决条件，故下文将对锚杆轴力定量建立多元线性回归模型，进而剥离温度影响的轴力，还原边坡变形对锚杆作用的真实轴力。

该处选取具有代表性的MGZ1342测点建立多元线性回归模型，由于该测点受降雨影响较小，暂不考虑降雨影响，故锚杆轴力主要受温度、开挖高程和时效变形影响，分别对3个因素进行量化：温度分量fT、边坡开挖分量fH、时效变形分量fθ[10]，所以锚杆轴力F为

F=fT+fH+fθ。

(1)

4.1 温度分量fT

温度变化直接影响到锚杆的膨胀与收缩，且锚杆热胀冷缩与温度之间呈线性关系，则锚杆轴力的温度分量可表示为

fT=β1(Tt-T0) 。

(2)

式中：t为观测日至首测日的累计天数；T0，Tt分别为首测日、第t日的实测日平均温度；β1为温度分量回归系数。

4.2 边坡开挖分量fH

根据边坡开挖高程离锚杆轴力测点越近，影响越大，反之离的越远，影响越小，可知锚杆轴力与边坡开挖的高程呈线性关系，同时锚杆轴力前期的突变与后期平稳，可知锚杆轴力的变化具有对数函数的性质，故边坡开挖引起的轴力分量fH可表示为

fH=β2(H0-Ht)+β3ln(H0-Ht) 。

(3)

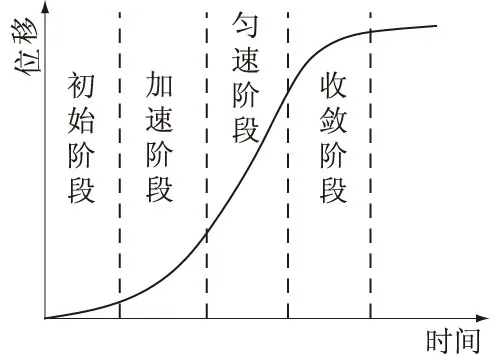
图4 边坡的一般时效变形

式中：H0，Ht分别为首测日、第t日边坡开挖的高程；β2，β3分别为边坡开挖分量回归系数。

4.3 时效变形分量fθ

边坡的一般时效变形如图4所示，由于边坡的开挖，初始阶段已不复存在，边坡的时效变形直接进入加速阶段，匀速阶段的边坡变形与时间呈近似线性关系，收敛阶段的边坡变形与时间呈对数函数关系，可见时效变形引起锚杆轴力也有这两种函数关系，故时效变形引起的轴力分量可表示为

fθ=β4θ+β5lnθ 。

(4)

式中：θ=t/100，其中t为观测日至首测日的累计天数；β4，β5分别为时效变形分量回归系数。

4.4 锚杆轴力回归统计模型

结合上述对各分量的量化，将各分量统计相加，如式(1)可知，本文锚杆轴力多元线性回归统计模型为

F=β0+β1Tt+β2(H0-Ht)+β3ln(H0-Ht)+

β4θ+β5lnθ。

(5)

式中β0为常数项，共含3个回归因子、5个回归系数。

4.5 回归模型结果分析

选取具有典型代表的MGZ1342测点进行锚杆轴力回归分析，轴力首次观测日为2009年9月28日，为保证能捕捉到开挖轴力的突变，对监测数据密集采集。从2009年9月28日至2013年6月12日期间共选取1 354组数据进行回归分析。MGZ1342测点部分监测值及影响因子如表2所示。

经回归分析，求得回归系数，拟合的相关系数为0.91，具有较高的拟合精度，拟合的效果如图5所示，回归模型表达式为

F=9.936 0-0.457 3Tt+0.004 5(H0-Ht)+

0.009 4ln(H0-Ht)+0.305 6θ+0.010 1lnθ 。

(6)

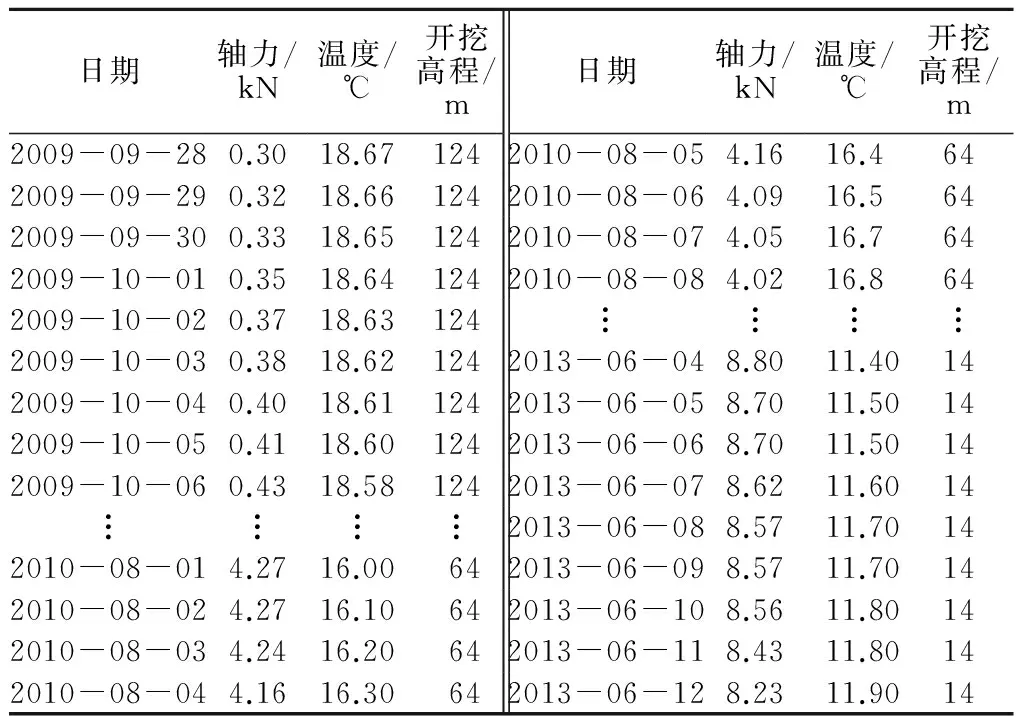
表2 MGZ1342锚杆轴力监测值及影响因子

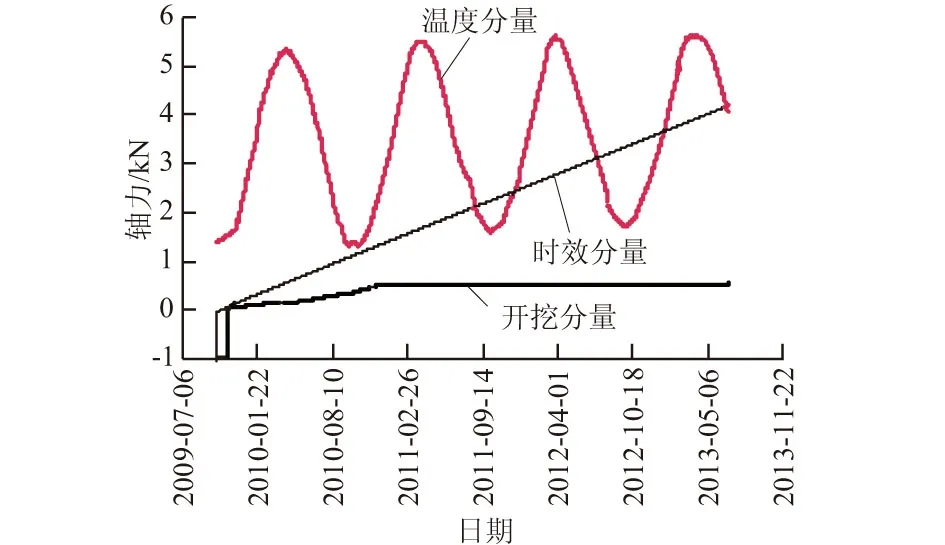
图6 MGZ1342锚杆轴力各分量对比

由式(6)可知，锚杆轴力与温度呈负相关性，与前文定性分析相一致。经过剥离温度的影响，锚杆轴力几乎与时效变形呈对数函数关系，如图5所示，此时锚杆最大轴力只有5 kN，这部分轴力最能反映边坡的变形性状，比没剥离温度锚杆轴力小约4.5 kN。将每个影响轴力的分量进行分离，各分量的变化趋势如图6所示，温度分量对锚杆轴力的影响幅度达到1.5～5.5 kN，最大值占锚杆轴力的57.95%，可见温度对锚杆轴力影响之大，使得多数锚杆轴力变化呈波动形式，正如表1统计一样。开挖分量对锚杆轴力的影响主要在监测仪器埋设初期，随着开挖面的降低直至开挖结束，开挖分量逐渐收敛稳定，开挖引起的轴力分量最大达到0.58 kN。时效变形主要呈线性变化，随着时间的变化所占比例逐渐增大，从图中可知，MGZ1342锚杆轴力具有逐渐增大的趋势，相对于锚杆的警戒值60 kN较小，该测点部位不存在岩体破坏，但值得长期观测。

针对MGZ1042测点锚杆轴力最大值近100 kN，超过警戒值，在工程中值得进一步分析剥离温度分量后的轴力，从而判断锚杆真实对边坡的加载作用力。同理，利用上述理论方法，建立了MGZ1042测点的多元线性回归模型。根据图7中MGZ1042锚杆轴力与温度变化曲线关系可知，锚杆轴力与坡表温度呈正相关性，侧面也印证了该部位的岩体破碎，测点温度相对于坡表温度变化幅度小，同时滞后于坡表温度，符合温度随边坡深度发展的规律。

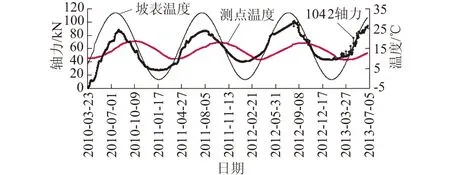
图7 MGZ1042锚杆轴力随不同部位 温度的变化曲线

MGZ1042测点锚杆轴力回归模型表达式为

F=10.984 9+0.141 8Tt+0.217 8(H0-Ht)+

1.689ln(H0-Ht)+1.657 2θ+0.057 3lnθ 。

(7)

图8 MGZ1042锚杆轴力实测值与拟合值对比

其拟合的相关系数为0.94，MGZ1042轴力实测值及拟合值如图8所示，拟合精度较高，剥离温度影

响的分量后，锚杆最大轴力只有40 kN，未超过警戒值，无需发出预警。同时相对于未进行温度修正轴力小60 kN，可见温度对锚杆轴力影响之大，这很容易造成对边坡变形破坏的误判。根据图9中各分量对比图可知，温度影响锚杆轴力波动幅度达60 kN，最大值近70 kN，故锚杆轴力必须经过温度修正方可对边坡稳定性作进一步的分析研究。

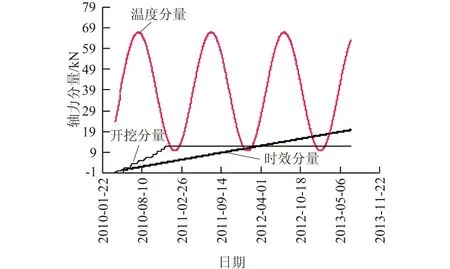
图9 MGZ1042锚杆轴力各分量对比

5 结 论

(1) 锚杆轴力主要影响因素有温度、降雨、边坡开挖及时效变形。其中温度起主导作用，锚杆轴力与其呈正相关或负相关，呈波动变化；边坡开挖对邻近的锚杆轴力有影响，往往导致锚杆轴力突变，呈“阶梯状”变化；锚杆轴力与时效变形呈一定的正相关。

(2) 对温度分量、开挖分量、时效变形分量进行了定量化，建立了MGZ1042，MGZ1342锚杆轴力多元线性回归模型，剥离了温度影响后，锚杆轴力都相应减少，尤其是MGZ1042减少了60 kN，从警戒值以上降到警戒值以下，还原了锚杆作用在边坡的真实轴力，从而降低了对边坡变形破坏的误判，做到科学指导工程生产。

(3) 从不同测点的拟合效果分析可知，锚杆轴力与坡面温度的拟合值高于锚杆轴力与测点温度的拟合值。故本文拟合模型更适合锚杆轴力与坡面温度呈正相关关系的成果分析，进而可避免锚杆轴力分析的失真。

[1] 郭冬生. 三峡永久船闸高强锚杆施工与锚杆应力分析[J]. 岩石力学与工程学报， 2002, 21(2): 257-260.

[2] 郭永建，王少飞，李文杰. 应力监测在公路岩质边坡中的应用研究[J]. 岩土力学， 2013，34(5): 1397-1402.

[3] 何忠明，蔡中心，曹 平，等. 层状岩体边坡锚杆加固效应的数值分析[J]. 中南大学学报(自然科学版)，2011, 42(7): 2115-2119.

[4] 王发玲，刘才华，龚 哲. 顺层岩质边坡锚杆支护机制研究[J]. 岩石力学与工程学报，2014，33(7): 1465-1470.

[5] 郭永建，孙 阳. 全长粘结锚杆在岩质边坡中的受力形式分析[J]. 力学与实践，2012, 34(3): 18-22.

[6] 朱焕春. 某边坡锚杆应力状态测试与分析[J]. 岩土工程学报，2000, 22(4): 471-474.

[7] 徐卫军，李 刚. 三峡永久船闸直立坡锁口锚杆应力监测分析[J]. 长江科学院院报， 2001, 18(1): 49-51.

[8] 黄清保. 岩质边坡锚杆应力影响因素分析[J]. 施工技术，2013, 42(23): 59-62.

[9] 刘祖强，廖勇龙，朱全平. 三峡永久船闸一期高边坡监测锚杆应力分析[J]. 长江科学院院报，2004, 21(1): 40-42, 46.

[10]李宏恩，李 铮，范光亚，等. 龙江水电站坝后厂房高边坡锚杆应力分析[J]. 水利水电科技进展，2012, 32(4): 59-62, 94.

[11]陈志坚，黄清保，王 霄. 岩质边坡锚杆及防护网温度应力分析[J]. 中外公路，2012, 32(5): 20-23.

(编辑：赵卫兵)

Analysis of Monitored Axial Force of Anchor in the Absenceof Temperature Influence

XU Jing-chun1, YU Jun-ping2, WU Li-jun3, YANG Zai-ren4

(1.Ganzhou Expressway Co. Ltd., Ganzhou 334100, China; 2. Jiangxi Transportation Research Institute, Nanchang 330200, China; 3.China Railway Tunnel Survey Design Institute Co. Ltd., Tianjin 300133, China;4.Guizhou Survey & Design Research Institute for Water Resources and Hydropower, Guiyang 550002, China)

Anchor bolt support is commonly used in slope reinforcement. Analysis on the causes of anchor’s axial force is of vital significance as the assessment of reinforcement effect is often dependent on the anchor’s axial force which is influenced by many factors. In this article, a multiple linear regression model of anchor’s axial force was established for a ultra-high rock slope of an expressway. Firstly, factors affecting the axial force were analyzed in qualitative terms, and then the factors were quantified. Furthermore, the real axial force was calculated in no consideration of temperature influence. The aim is to accurately assess the anchorage effect and reduce misjudgment of slope deformation. The model was applied to the calculation of real axial force at point MGZ1042 of the anchor bolt. In the absence of the influence of temperature, the axial force fell from 100kN to 40kN, not exceeding the monitoring alarm value 60 kN.

rock slope; axial force of anchor; monitoring; temperature influence; regression model

2015-10-30；

2015-11-21

江西省交通运输厅重点工程科技项目(2015C0067,2016C0004,2015C0020)

许景春(1976-)，男，江西赣州人，高级工程师，主要从事公路建设与工程管理科技工作，(电话)15070948368(电子信箱)766105260@qq.com。

10.11988/ckyyb.20150922

2017,34(1):81-86

TV698.11

A

1001-5485(2017)01-0081-06