基于改进KD树与RANSC算法的目标识别算法

岑丽

（中国航发控制系统研究所江苏无锡214063）

无人机（Unmanned）Aerial Vehicle，UAV）作为无人机驾驶的航空飞行器，近年来不管在军用，或者是民用上，都得到了广泛的发展。而在此过程中，无人机的功能性或多或少会依赖于其搭载的摄像机，正是实时图像的获取使得无人机能完成各种任务，例如目标跟踪、测绘测量和侦查打击等[1]。摄像机只是充当了信息采集的工作，真正的处理工作其实是由计算机完成。因此，计算机视觉技术的应用正是无人机得到快速发展的一大要素。

在无人机的任务中，涉及到的计算机视觉技术，无外乎去除噪声、目标识别、目标定位以及目标跟踪等[2]，本文主要针对无人机上广泛应用到的目标识别技术进行研究。

目标识别就是指从一副（或多副）图像中找出与给定目标图像相似的图像区域的过程。通常将已知的目标图像称为模板图像，将待查找图像称为目标图像。由于在无人机任务过程中，算法必须能适应工作环境、光照、视野角度等对目标图像的影响，基于以上考虑，本文论述的目标识别技术主要是依据特征点的识别。特征点具有比例尺度不变等诸多优势[3]。特征点算法繁多，较为常用的有SIFT、SURF、Haar和 FAST等，其中 SIFT（Scale-Invariant Feature Transform）算法是由Lower等人提出的一种图像比例不变特征提取方法，该方法是在尺度空间中搜寻极值来获取特征点的位置、旋转、尺度不变量，因此算法的鲁棒性较强[4]。在完成特征点提取之后，需要进行的是模板图像特征点与目标图像特征点的识别匹配，以此找出目标所处区域，对于该过程，本文主要分为两个步骤：粗匹配和精匹配[5]。其中粗匹配采用的是改进KD树（K维搜索树）匹配算法[6]，该算法具有匹配速度快的特点。在本阶段将过滤到大部分噪声特征点，但还无法做到特征点的一一对应，可能会出现一对多的匹配关系。精匹配采用的是RANSC（Random Sample Consensus，随机抽样一致）算法，该算法由Fischler和Bolles于1981年提出，在精匹配阶段能剔除绝大部分误匹配点。

1 SIFT特征点提取过程

定义L(x,y,σ)为图像I(x,y)的尺度函数[7]：

其中*表示卷积，G(x,y,σ)表示一个尺度可变的高斯函数：

其中，(x,y)表示空间坐标；σ为尺度坐标，表示图像的平滑程度。

在高斯差分DoG（Difference of Gaussian）尺度空间中寻找极值点，则有：

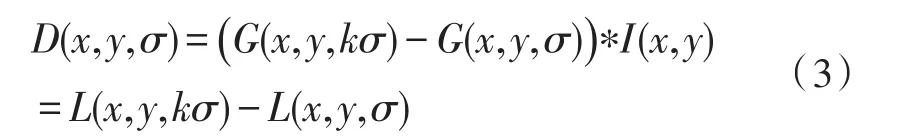
为了让算子拥有旋转不变性，设置方向参数为：

上式表示的分别是(x,y)处的梯度数值m(x,y)和角度方向θ(x,y)，其中L选用的是每个关键点各自所在的尺度[8]。

图1表示的用SIFT算法生成的模板图像与目标图像的特征向量。

图1 SIFT特征向量图

2 改进KD树粗匹配

2.1 KD树

KD树是一种二叉树，是把二叉搜索树推广到多维数据的一种主存数据结构，由Bentley于1975年剔除[9]。其与二叉树的不同之处在于，其节点表示的是K维空间中的一个点，且树的每一层都是依据该层分辨器做出的分支决策。

原来的KD树匹配算法，采样的是最临近点查找法，该算法采用深度优先启发式搜索策略。首先需要定义超矩形（hyper-rectangle）hr与以目标点t为中心半径为r的超球体相交，求出hr中与圆心最经的点P，点P由下式计算：

其中Pi和ti表示点P和目标点t在第i维上的取值分别表示超矩形在第i维上的最小值和最大值[10]。

若p与t欧式距离小于半径r，则两者相交。此法需要首先比较目标点与KD树节点的距离，再根据目标点在节点维数上取值来决定左右树查找。

本法在样本点维数过多时，容易对特征点进行错分，导致无法匹配到最近的特征点。因此需要进行算法该进。

2.2 改进的KD树匹配算法

基于识别精度的考量，对KD树的匹配算法进行了如下改进[11]：

1）对分割维数按一定优先级排序，排序标准是维数之间的相关性，这样的做法可以使得对其他维数影响较大的排在前面。

2）当发现某个维数下的样本数过少是，则直接遍历余下点。

根据样本数据集特点，可对维数优先级进行分析，这里的优先级是以样本集中维数之间的相关性作为准则的。实际应用中，使用主成分分析做优先级依据。

主成分分析[12]是对多变量数据进行统计处理的一种数据线性投影的方法。它能够将高维空间样本映射到低位主成分空间上，同时又能保留原有信息不丢失。

对于大小为M，以N维的梯度信息来描述特征点的样本集E。通过以下步骤，计算出主成分奉献率。

令

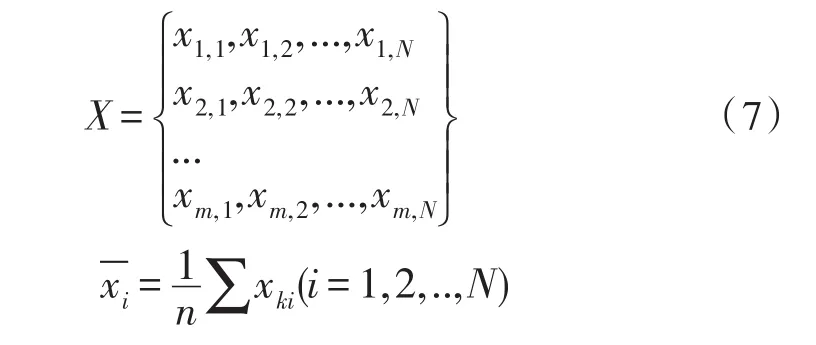
计算相关矩阵R=r(i,j)，

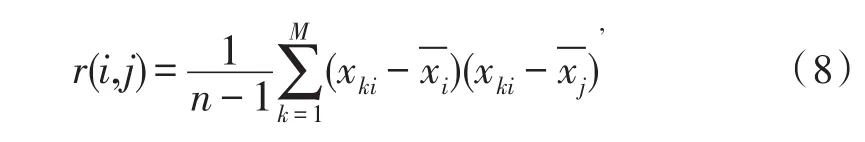
计算主成分奉献率：

按照Ci得到数组D[n]，它根据主成分奉献率从大到小存储特征点维数。在得到D[n]后，构造树时，需要添加节点权值。首先需要按维数优先级排序好的D[n]中的维数顺序构造KD树。

建立好改进的KD树之后，统计出到达某叶子节点的样本数占总样本百分比，记为该节点的样本节点权值q。然后对树进行后序遍历，使得q=qr+ql，其中qr表示该节点右子树概率，ql表示该节点左子树概率。

在查找时，只需要增加节点权值的验证即可，即做阈值判断。

下面两张图分别表示使用改进KD树匹配算法的匹配效果前后对比。可以很明显的看出使用改进KD树算法比改进前的KD树，产生更少的匹配点。尽管如此，由于某些应用环境对目标识别效果的要求较高，因此需要在改进后的KD树匹配算法下再进行下一步的精匹配。

图2 改进前后KD树匹配效果图

3 RANSC精匹配

RANSC算法是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据的算法。这种算法的基本假设是样本中包含正确数据（适应模型的数据），也包含异常数据（不适应模型的数据）。而且给定一组正确的数据，存在可以计算出符合这些数据的模型参数的方法[13]。

以经过KD树匹配的特征点作为样本数据集。在考虑平移、旋转和尺度变化的影响下，以模板图像中两角点间的距离与目标图像中对应两角点间的距离之比作为需要确定的数学模型[14-15]。

主要的精匹配过程如下：

1）在模板图像和目标图像的粗匹配点中随机选择两组特征点（Up1，Down1）和（Up2，Down2），并将两个点组计入当前模型的数据点集合this_consensus_set中；Up表示模板图像特征点，Down表示目标图像特征点；

2）建立本次计算的模型参数Model=

3）遍历除了1）中选出的两组点以外的其他点组，并计算每对点组 i（Upi，Downi）与 1）中两个点组之间的伪模型值若Model1与Model2与Model之间的偏差同时小于模型阈值dt，则认为点组i匹配正确，计入当前模型的数据点集合this_consensus_set中。

4）若最终this_consensus_set的数据个数set_num超过阈值st，则进入5）;否则，计算次数iterations加1，并返回步骤1）。

5）计算模型偏差this_error；

以this_consensus_set为计算集合，遍历所有点组，计算每一点组与其他点组的伪模型值与当前模型参数的偏差，并将所有偏差相加开方，即可得到this_error。

6）若 this_error小于模型偏差阈值 best_error，则认为匹配完成，认为this_consensus_set中的匹配点组即为最终的匹配结果。否则，计算次数iterations加1，并返回步骤1）。

图3是在改进KD树粗匹配的基础上再使用RANSC算法完成精匹配的结果，可以看出经RANSC算法后，本次匹配剔除了所有的误匹配点，匹配效果较好。同时仔细观察可以发现，模板图像在目标图像中有不仅存在尺度变化、同时还有旋转变化，但算法的实现将二者的影响都成功消除了。

图3 采用RANSC精匹配效果图

4 结论

文中通过分析图像识别算法在无人机上的应用环境，确定使用SIFT特征点作为基本算子，然后将识别过程分为粗匹配和精匹配两个过程，其中的粗匹配拟采用KD树匹配算法，但因其在实际使用中出现大量错分情况，因此进行了算法改进，改进后的KD树[16-17]匹配所产生的无匹配点明显减少。为了能够得到更好的匹配效果，在改进KD树匹配后，采用RANSC精匹配算法，完成最后的匹配，通过实验可以看出，采用基于改进KD树和RANSC算法的匹配效果较好，误匹配点基本剔除。

[1]黄敦华，朱青松.基于微小型四旋翼飞行器的目标监测与识别综述[J].机电产品开发与创新，2011，24（6）：16-18.

[2]张志飞.小型无人直升机视觉定位与跟踪系统的设计与研究[D].杭州：浙江大学，2013.

[3]息朝健，郭三学.基于简化Forstner算子改进的SIFT无人机图像识别算法[J].计算机应用于软件，2012，29（5）：254-256.

[4]郑刚.基于特征的图像匹配算法研究[D].长沙：国防科学技术大学研究生院，2011.

[5]韦东兴，陈晓云，徐荣聪.基于角点检测的图像形状特征提取方法[J].计算机工程，2010，36（4）：220-222.

[6]王渊民.基于SIFT算法的图像快速匹配系统设计[D].成都：成都理工大学，2014.

[7]汤伯超.基于SIFT算法的图像特征描述方法研究[D].广州：广东工业大学，2012.

[8]朱玮.基于视觉的四旋翼飞行器目标识别及跟踪[D].南京：南京航空航天大学，2011.

[9]杜振鹏，李德华.基于KD-Tree搜索和SURF特征的图像匹配算法研究[J].计算机与数学工程.2012，40（2）：96-98.

[10]杨晶东，杨敬辉，洪炳镕.移动机器人视觉图像特征提取与匹配算法[J].计算机应用研究，2009，26（9）：3526-3529.

[11]熊云艳，毛宜军，闵华清.有序的KD-tree在图像特征匹配上的应用[J].化工自动化及仪表，2010，37（10）：84-87.

[12]马莉，韩燮.主成分分析法（PCA）在SIFT匹配算法中的应用[J].电视技术，2012，36（1）：129-132.

[13]张勇，余建平，孙军伟，等.基于Harris的角点匹配算法研究[J].计算机与现代化，2011（11）：78-81.

[14]杨健，李若楠，黄晨阳，等.基于局部显著边缘特征的快速图像配准算法[J].计算机应用，2014，34（1）：149-153.

[15]刘如飞，卢秀山，刘冰，等.一种改进的无人机航摄影像快速拼接方法[J].测绘通报，2014（2）：46-49.

[16]邹艳荣，郑政.一种用于高频超声探头的扫描电机及控制系统[J].电子科技，2016（10）：111-114.

[17]汪立，蒋念平.基于改进Harris角点检测的视网膜图像配准[J].电子科技，2017（2）：119-122.

[16]邹艳荣，郑政.一种用于高频超声探头的扫描电机及控制系统[J].电子科技，2016（10）：111-114.

[17]汪立，蒋念平.基于改进Harris角点检测的视网膜图像配准[J].电子科技，2017（2）：119-122.