基于自适应卡尔曼滤波的GPS/INS位置组合导航

许根源，王直，王志强

（江苏科技大学电子与信息学院，江苏镇江212003）

在控制工程领域中各种系统都需要能够完成对系统的有效控制，精确有效的控制系统无一例外的都是闭环控制系统，闭环控制中系统状态反馈的准确把握是系统能否有效控制的主要判定标准。实际的工程控制领域包含多种控制方法，其中对系统的过去、未来及现在的状态的控制检测为常见的典型控制系统。对特定系统的精确控制需要特定的观测手段，只有通过这些特定的观测手段才可以估计出系统过去、现在、未来的状态，进而达到对系统已知状态的评估，实时状态的精确控制，控制趋势的准确预测等。在估计控制系统的状态的过程中最优估计显得尤为重要，实际系统在观测过程中存在来自系统本身的误差，检测元件误差，系统外部干扰等，这些干扰在控制理论中被定义为噪声。寻求滤除噪声干扰的方法直接影响系统的稳定性及精确性，故最佳系统状态估计必须解决噪声干扰的问题[1]。

为解决系统噪声干扰的问题多种控制算法应运而生，其中Kalman滤波等一些滤波算法在解决噪声干扰方面效果明显。Kalman滤波采用实时递推其数据存储量较小同时滤波算法简单易行方便移植多种控制器，在工程应用中成为一种备受重视的最优估计理论与方法[2-3]，在信号采集处理、工业轨迹控制、GPS导航定位等各种工控领域被广泛的应用。

1 自适应Kalman滤波

1.1 Kalman滤波方程

设控制对象的离散模型为：

上式u（k）为模型的m维控制向量，x（k）为模型的n维状态向量，v（k）为离散模型的n维过程干扰向量，y（k）为模型的r维输出向量，w（k）为r维测量噪声向量。假设W为正定对称阵，V为非负定对称阵，并且v（k）、w（k）不相关，w（k）为离散的高斯白噪声。v（k）为离散的高斯白噪声序列。

一步预测方程：

一步预测均方误差方程：

状态估值计算方程：

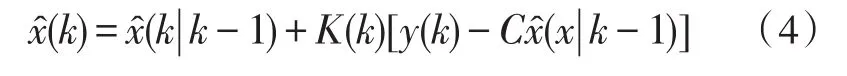
其中，K（k）为状态估计器或Ka1man滤波增益矩阵是x（k）的一步最优预报估计是 关 于y（k）的 一 步 预 报 估 计 ，是 关 于y（k）的 一 步预报估计误差。为了获得x（k）最小状态估计值，令状态估计误差的协方差最小，则有：

滤波增益方程：

上列式（2）～（6）构成了Ka1man滤波递推公式。

1.2 自适应卡尔曼

在应用中理论特性应与实际的余项相匹配，实际的余项应该在滤波的过程中被实时的检测，以保证滤波过程中实际的余项不会出现异常。实际的余项不相容原假设Q（k-1）、R（k-1）时，原来假设的Q（k-1）、R（k-1）应该用Q（k）、R（k）的重新估计来取代。其常用判据为[4]：式中γ＞1为储备系数；tr为矩阵的迹；v（k）为信息序列。

v（k）方差的理论值为：

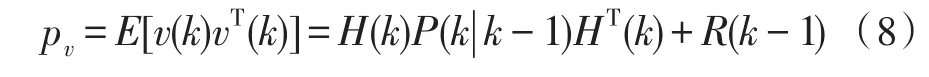
v（k）的实测方差为：

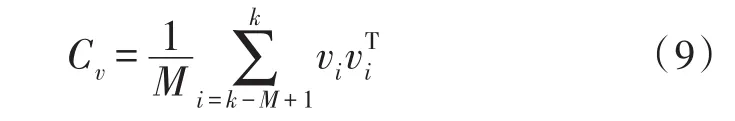
可得到滤波严格收敛判据为[5]：

上式中，Var(k)为滤波状态因子，Var(k)≠1时称为滤波异常，Var(k)=1时称为滤波严格收敛。Var(k)＞1或Var(k)＜1的量测噪声增大或减小，调节（k）增大或减小，可以使Var（k）在1附近变化，这样就可以实现滤波的多种适应性[2]。

2 状态、观测方程的建立

在航空空间技术中卡尔曼滤波也因其优越的特性被广泛的应用。在测轨问题和惯性导航等方面卡尔曼滤波发挥这重要的作用。所谓测轨问题就是通过观测飞行器在不同时刻的状态数据，然后应用卡尔曼滤波方法对这些数据分析，估计出飞行器各个时刻的位置、速度、加速度及阻力系数等物理量这些都被称作状态变量。这些状态变量作为系统的反馈为控制系统提供精确的控制数据，这样控制系统便可以控制飞行器进行导航、制导和拦截等动作。文中主要研究在GPS/INS组合导航的方法中如何更好的运用滤波算法提高飞行轨迹精度。

在GPS/INS组合导航系统中使用的是线型卡尔曼滤波器，线型卡尔曼滤波器应用于组合导航系统时多用间接估计法。组合导航系统中的误差状态较多且类型不一，在导航系统中将这些误差统称为误差组合体。滤波器根据系统误差估算出的误差估值ΔX是控制系统的重要控制参数，在惯性导航系统中需要用误差估值ΔX来对导航系统的控制参数进行精确的矫正。根据导航系统中最典型的平台误差，速度误差以及位置误差可以建立导航系统的模型方程。

INS/GPS组合模型的逼近线性离散时间系统如下：

式中，Xk和Zk分别为被估计的状态向量和观测向量：Φk,k-1和Hk为状态转移矩阵和观测矩阵；Wk为导航系统的过程噪声，Vk为导航系统的量测噪声，过程噪声和量测噪声是相互独立的，同时是带时变均值和协方差的正态白噪声序列。

其中，q(k)、Q(k)为导航系统的过程噪声，Wk时变均值和协方差，r(k)、R(k)为导航系统的量测噪声，Vk时变均值和协方差。

导航系统多为多传感器组合导航系统，为了便于对导航系统做深入的研究，导航基准坐标系采用东、北、天坐标系，用此坐标系作为车辆导航定位[3]的基准坐标系。在分析研究INS及GPS组合导航系统的性能及误差数据时，取15维状态矩阵、9维观测矩阵，并采用位置、姿态组合观测[6-7]：

其中，δPe、δPn、δPh为相对切平面位置误差，δVe、δVn为速度误差，δα、δβ、δβ为平台角姿态误差，∇cx、∇cy、∇cz为加速度计零偏，εcx、εcy、εcz为陀螺常值误差[4]。

3 算例仿真

3.1 仿真流程图

仿真流程图如图1所示。

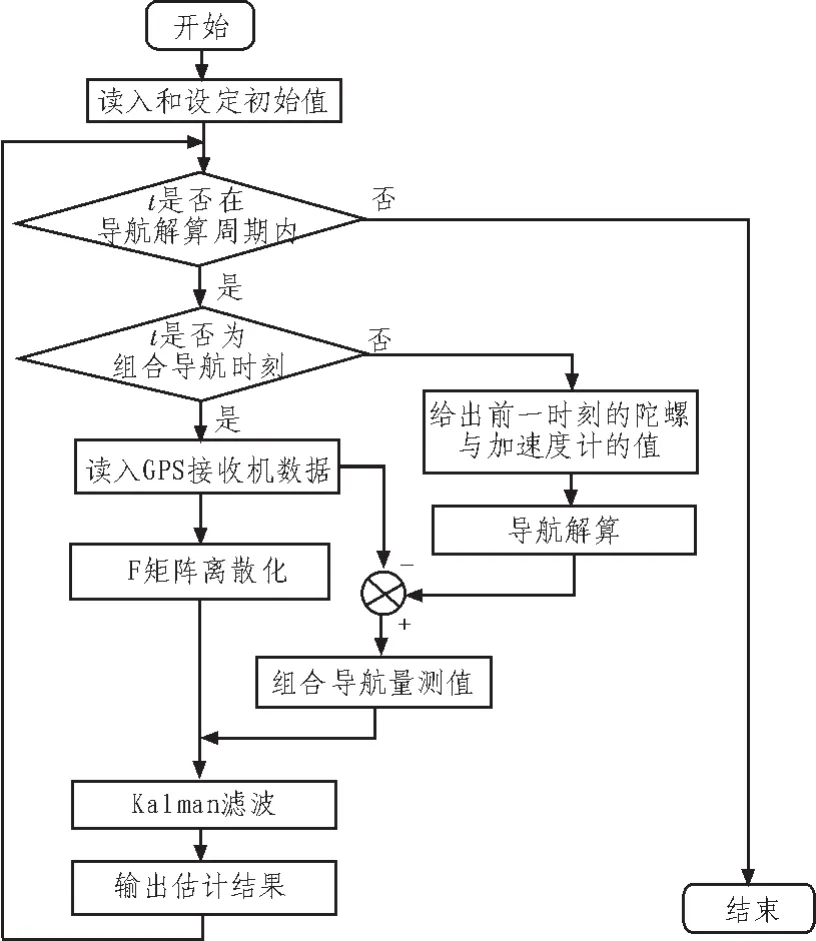
图1 仿真流程图

3.2 仿真结果

3.2.1 普通Kalman滤波

根据仿真分析先利用飞行轨迹发生器产生一组状态数据，对这组状态数据进行Kalman滤波，如图2是飞行轨迹发生器产生状态数据得到的轨迹图。

分析位置误差需要先将位置误差进行放大，放大比较可以将不明显的位置误差变为易于观察。

图2 飞行轨迹图

图3是放大的误差比较图，从图中很容易观察出Kalman滤波后误差比滤波前小很多。通过观察图4速度误差比较图，Kalman滤波[5]后速度追踪误差减小很多。通过对比可得出采用Kalman滤波后的导航系统精确度优于只用INS的导航系统，综合分析Kalman滤波整体滤波效果明显。

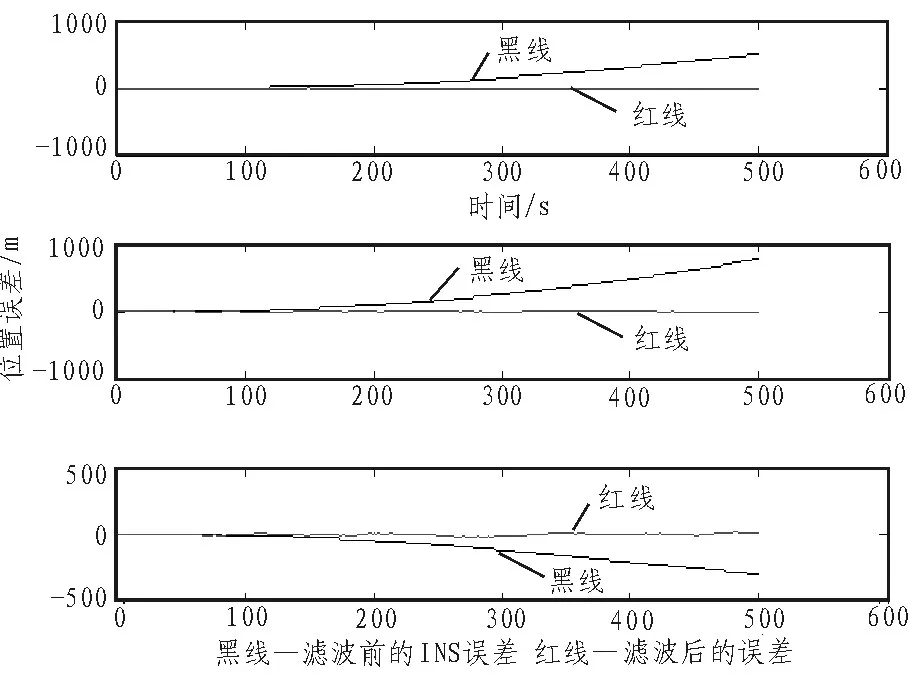
图3 位置误差比较图

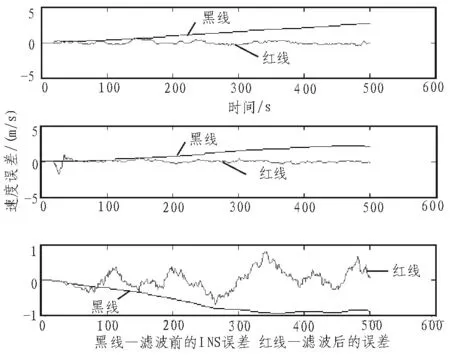
图4 速度误差比较

3.2.2 自适应Kalman滤波

自适应Kalman滤波如图5、6所示。

3.2.3 自适应与非自适应Kalman滤波比较

可以看出随着时间的推移，自适应Kalman滤波[6]有较少的误差，误差的波动也比非自适应小。

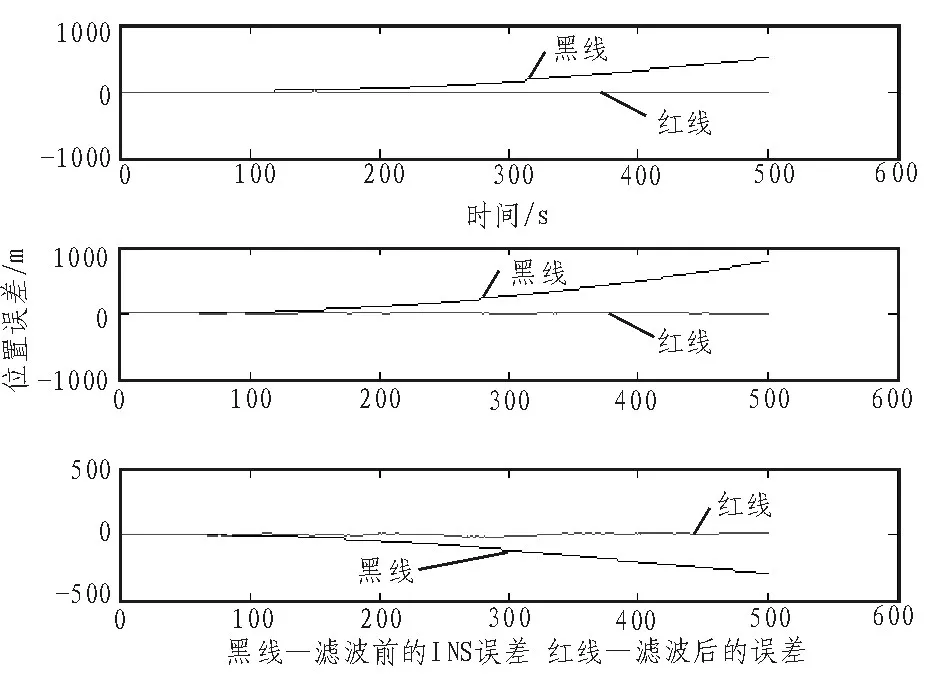
图5 位置误差比较图

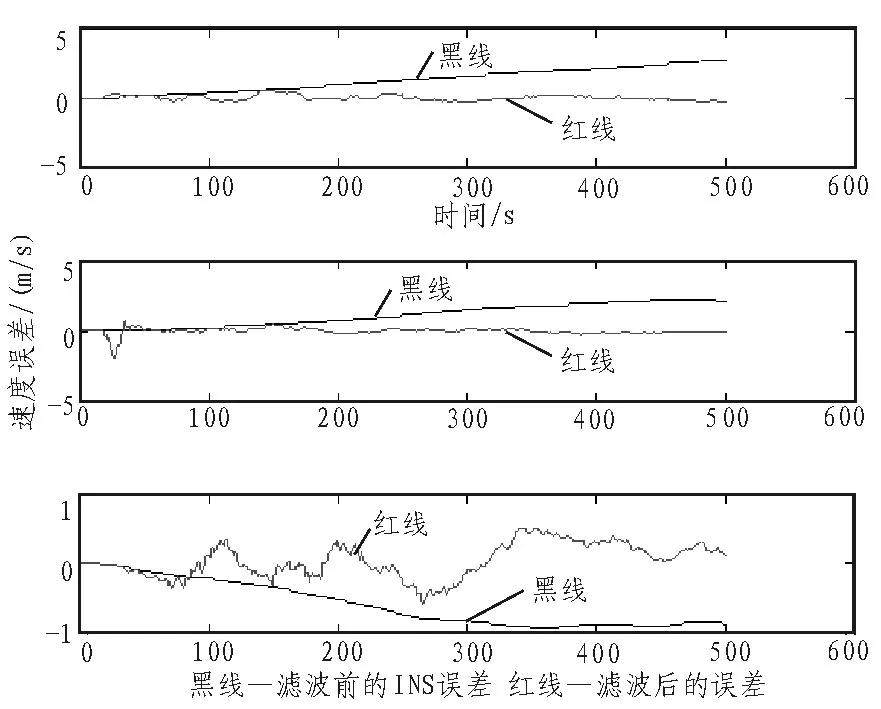
图6 速度误差比较

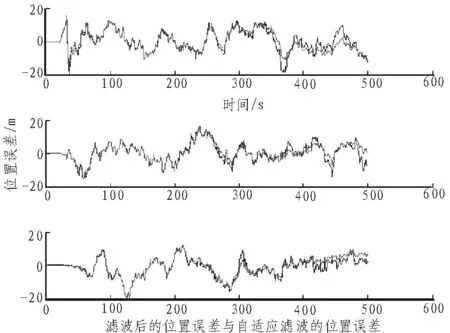
图7 自适应与非自适应位置误差比较

根据以上的仿真数据分析，采用自适应Kalman滤波的导航系统相比于单纯采用标准Kalman滤波的导航系统有更好的滤波效果。

4 结论

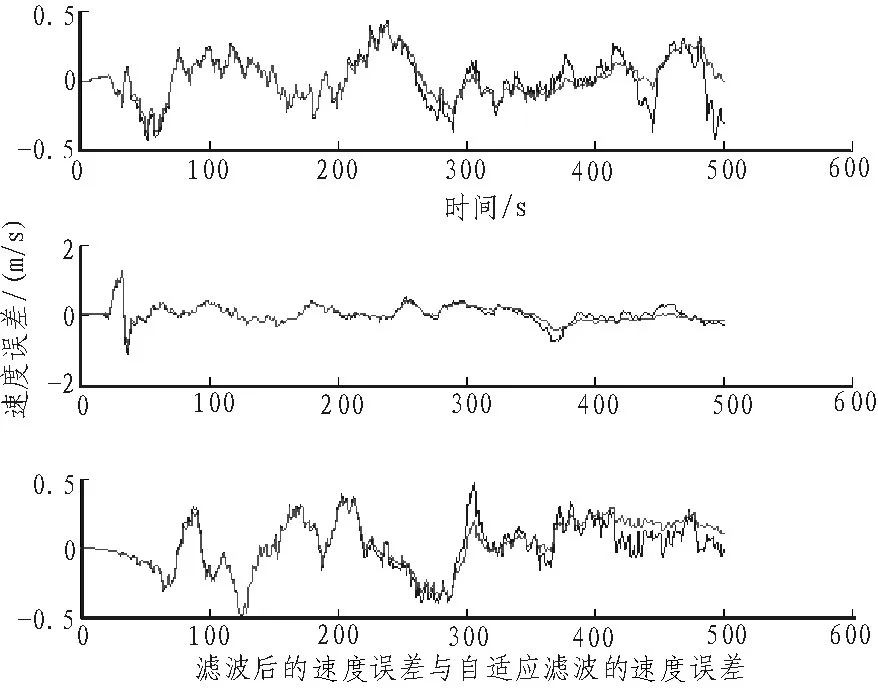
图8 自适应与非自适应速度误差比较

Kalman[16-17]滤波器的最优估计不仅可以应用于对系统状态估计而且在智能控制算法中的可以利用Kalman滤波器的最优估计参数调整加快系统速度。Kalman滤波算法会有更多的扩展应用及继续发展，能够扩展的地方还有很多。标准Kalman滤波在实际使用中会存在一些局限性[7]，此时就应当进行相应的优化，在一些特定的控制系统中采用自适应Kalman滤波将会比较好的控制系统误差。自适应Kalman滤波具有很高的工程价值。

[1]韩崇昭，朱洪艳，段战胜.多源信息融合[M].北京：清华大学出版社，2010.

[2]周卫东，乔相伟.QUKF算法及其在SINS初始对准中的应用[J].仪器仪表学报，2010（2）：264-269.

[3]王甫红.高精度星载GPS实时定轨卡尔曼滤波模型[J].武汉大学学报：信息科学版，2010，35（6）：653-656.

[4]钱华明，葛磊，彭宇.多渐消因子卡尔曼滤波及其SINS初始对准中的应用[J].中国惯性技术学报，2012，10（3）：287-291．

[5]许长辉，高井祥，王坚．GNSS/INS组合系统的抗差卡尔曼滤波[J].中国矿业大学学报，2010，39（5）：773-778.

[6]徐彦田，程鹏飞，蔡艳辉，等.估计对流层延迟的单频RTK卡尔曼滤波算法[J].测绘通报，2012（8）：4-6.

[7]宋迎春.GPS动态导航定位的当前统计模型与自适应滤波[J].湖南人文科技学院学报，2010，10（5）：7-9.

[8]苏宛新，黄春梅.自适应Kalman滤波在SINS初始对准中的应用[J].中国惯性技术学报，2010，18（1）：44-47．

[9]孙枫，唐李军．基于CubatureKalmanfilter的INS/GPS组合导航滤波算法[J].控制与决策，2012，27（7）：1032-1036.

[10]Rigatos G G.Sensor fusion for UAV navigation based onderivative-free nonlinear Kalman Filtering[C]//Proceedingsof the 2012 IEEE International Conference on Roboticsand Biomimetics，2012，12：890-895.

[11]彭惠，熊智.IMU安装及标度因数误差动态参数辨识方法[J].中国空间科学技术，2014（1）：42-49.

[12]杨玲，沈云中，楼立志.基于中位参数初值的等价权抗差估计方法[J].测绘学报，2011，40（1）：28-32.

[13]刘江，蔡伯根，唐涛，等．基于CKF的GNSS/INS列车组合定位鲁棒滤波算法[J].交通运输工程学报，2010，10（5）：102-107．

[14]陈有荣，袁建平．一种改进的INS/GPS组合导航鲁棒H∞多重渐消容错滤波算法[J].宇航学报，2009，10（3）：930-936.

[15]邓海峰，高井祥.简化5级-GKF在SINS大失准角初始对准中的应用[J].测绘科学技术学报，2014（5）：473-476．

[16]闫丽荣，高爱华，杨捷.谐振法测量损耗卡尔曼滤波数据处理[J].西安工业大学学报，2015（8）：603-608.

[17]杨曼，李仁忠，刘阳阳，等.基于改进迭代匹配滤波的织物疵点检测[J].西安工程大学学报，2017（3）：383-389.