非包容转子爆破对飞机增压舱释压率的计算方法研究

张健

摘 要：飞机增压舱在高空受非包容转子碎片撞击受损后，会出现高空释压的问题，客舱内的压力会迅速减小。飞机增压舱发生破损后，飞机结构能够承受的载荷将发生变化，若要以最大速度下降可能会发生机体结构二次破坏的危险。因此，本文通过理论计算得出不同等效泄漏面积的释压率；根据不同的释压率，计算得出飞机紧急下降的安全速率。

关键词：非包容转子爆破；飞机增压舱；释压率

中图分类号： V215.9 文献标识码： A 文章编号： 1673-1069（2016）35-162-2

2 简化释压过程的数值仿真

根据上一小节得到的理论公式，利用Mathematica软件对飞机增压客舱突然释压过程进行数值计算。

2.1 数值仿真

飞机在巡航高度发生意外释压时，飞行机组人员要按照标准程序操作进行紧急下降，紧急下降的速度是飞机结构能承受的最大速度，最大速率约为每分钟4000到5000英尺。但若飞机发生非包容事故，并且增压座舱发生破损后，飞机能够承受的极限载荷将发生变化。因此，根据适航规章的规定，本文将计算得出不同下降速率对应的临界释压等效面积。

根据分析的可知，飞机发生突然快速释压前22s为机组人员的反应时间。因此，飞机下降的过程为：0—22s为机组准备下降过程，22s后为飞机紧急下降过程。

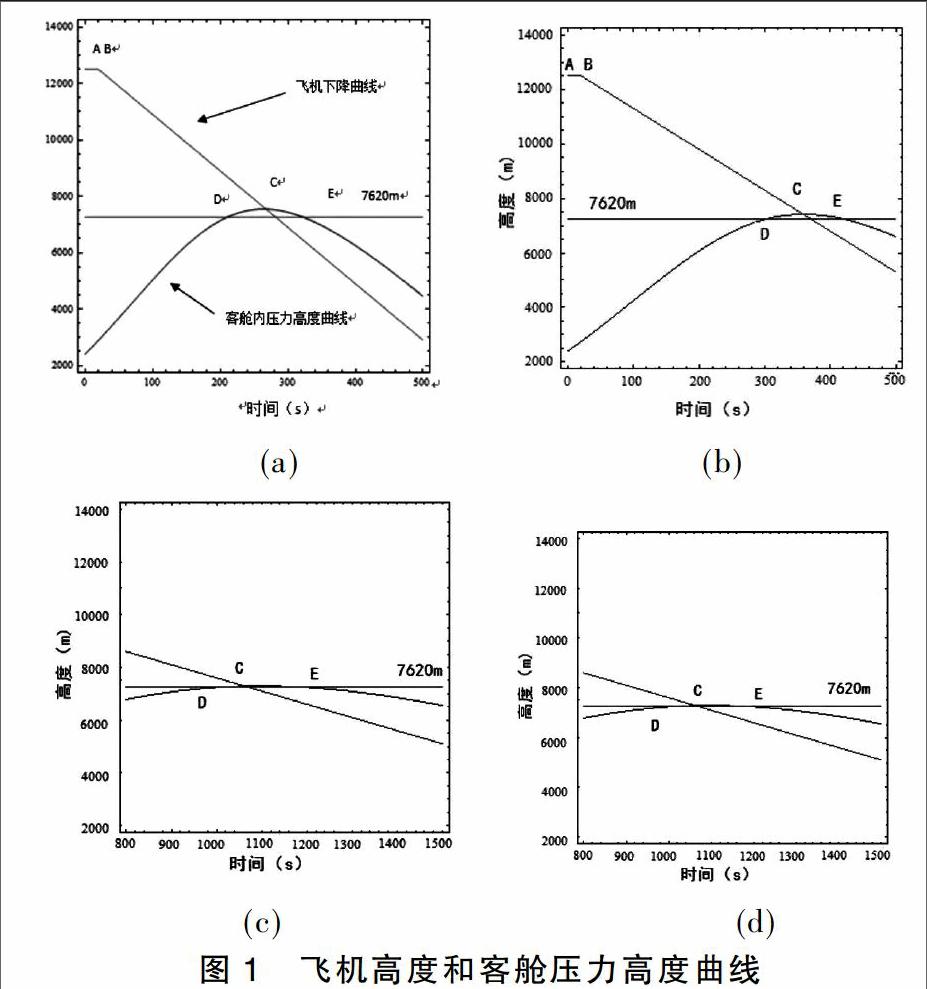
飞机的巡航高度为12500米，飞机下降速率为20m/s，规章要求的临界高度为7620米，临界时间长为120秒，如图1（a）所示。

图1（a）中，横坐标为时间，纵坐标为高度。A-B为前22秒机组的反应时间，此时飞机仍在巡航高度飞行且没有下降，但此时客舱内压力高度已经开始上升；C点为飞机的实际高度的与飞机增压舱内的压力高度相等的时刻；D-E的时间长为120秒，即飞机座舱压力高度大于7620m的时长为120秒；从C时刻开始，飞机客舱内的压力高度将随飞机实际高度降低而降低，但受破损洞口面积大小的限制，客舱内压力高度没有飞机下降的高度快，因此存在延迟现象。

经过计算得出，飞机的巡航高度为12500米，飞机下降速率为20m/s时，对应的临界等效面积为0.014平方米，对应的前22秒的飞机客舱压力高度的上升速率为24.85m/s。

如图1（b）所示，飞机的巡航高度为12500米，飞机下降速率为15m/s时，对应的临界等效面积为0.00988平方米，对应的前20秒的飞机客舱压力高度的上升速率为17.5m/s。

如图1（c）所示，飞机的巡航高度为12500米，飞机下降速率为10m/s时，对应的临界等效面积为0.00632平方米，对应的前20秒的飞机客舱压力高度的上升速率为10.75m/s。

如图1（d）所示，飞机的巡航高度为12500米，飞机下降速率为5m/s时，对应的临界等效面积为0.00311平方米。

利用上面的方法，对不同巡航高度的飞机，分别使飞机下降速率为20m/s、15m/s、10m/s和5m/s时进行仿真计算，得出相应的数据。

2.2 数据分析

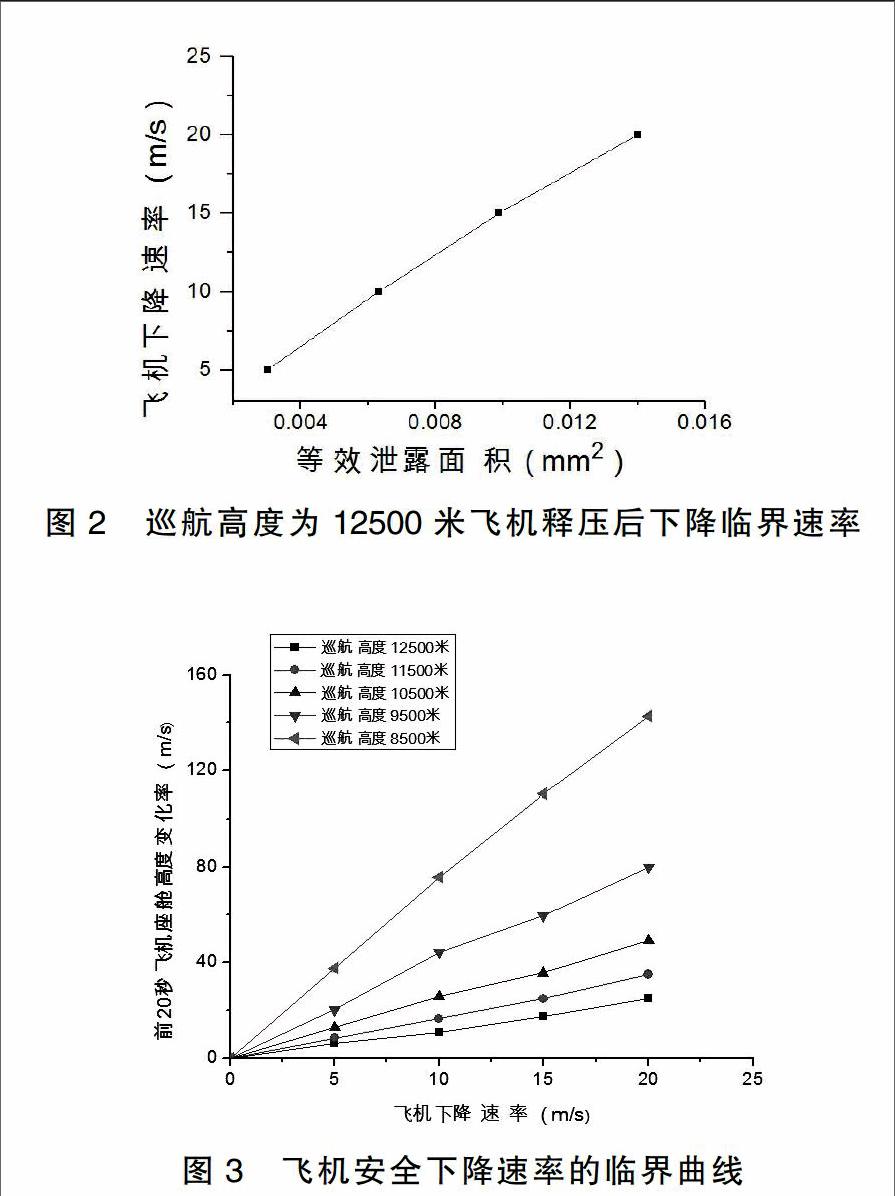
根据上面计算得出的数据，绘制出飞机下降速率—等效泄漏面积的曲线图，如图2所示。

根据计算后的结果可得2的曲线图，曲线的横坐标代表飞机的等效泄漏面积，纵坐标代表飞机下降速率，曲线代表某一等效泄漏面积下的临界下降速率。在某一等效泄漏面积下，飞机的下降速率应在图2临界曲线的上方，但应小于飞机结构能够承受的最大下降速率。

飞机增压舱破损后，飞行人员并不知道增压舱受损的泄漏面积，而仅仅可以根据飞机座舱高度仪表知道飞机座舱高度的变化率。因此，根据理论推导公式，求出前22秒的平均座舱压力高度变化率，将等效泄漏面积转化为座舱高度的变化率。根据假设我们知道，飞机的前22秒还没有进行紧急下降，所以可以将等效泄压面积变换为前22秒的平均座舱压力高度变化率。转化后如图3所示，曲线代表飞机下降速率的临界下降速率。飞机下降速率大于该临界的下降速率，才能满足适航规章的要求，即飞机的下降速率应在临界曲线的右侧。

图3 飞机安全下降速率的临界曲线

3 结论

①本文通过理论分析对释压率的公式进行了简化公式推导，得到座舱压力高度随飞机下降的时间函数；然后对增压舱泄漏量的计算公式进行了分析。②本文根据所推导出来的理论公式，依据CCAR25.841中客舱压力高度为7620米时不能超过2分钟的要求，利用Mathematica软件对飞机增压客舱突然释压过程进行数值计算，得到不同等效面积对应的释压速率；再分别计算不同飞行高度下的释压率，进而得到飞机相应的临界下降速率，最后得到飞机安全下降速率的临界曲线。

参 考 文 献

[1] 中国民用航空总局.CCAR-25-R3中国民用航空规章第25部[S].北京：中国民用航空总局，2001.

[2] 美国联邦航空管理局.AC20-128A[S].华盛顿：美国联邦航空管理局，1997.

[3] 蒋龙富，刘鹏.座舱允许最大泄漏量与等效泄漏面积的计算及分析[J].民用飞机设计与研究，2006（11）：31-32.

[4] 彭世尼，周廷鹤.燃气泄漏与扩散模型的探讨[J].煤气与热力，2008（2）：56-58.