浅谈中学生数学发散思维能力的培养

翟洪祥

（吉林省辉南县抚民镇中学）

浅谈中学生数学发散思维能力的培养

翟洪祥

（吉林省辉南县抚民镇中学）

发散思维是指不以常规，寻求变异，沿着不同的方向、不同的角度对信息进行分析和重新组合，从多方面寻求问题答案的思维形式。

发散思维；问题；变式训练

在学习几何中，发散思维是指根据定理、定义公式和已知的条件，让思维朝着多个可能的方向发展，不局限于现有的模式，从多个角度寻找解决问题的有效的方法。要想提高思维发散能力，克服现有思维定势，在教学中应该从以下几个方面加强训练：

一、对问题的条件进行发散训练

当问题的结论确定之后，尽量改变已确定条件，可以从不同角度，用不同的知识解决问题，这就是对问题的条件进行发散训练。例如，已知：如图1，OA=OD，请你添加一个条件，使ΔABO≌ΔDCO。比如可添加∠A=∠D；∠B=∠C；AB∥CD，OB=OC。这样，既揭示了数学问题的层次性，又充分暴露了学生自身的思维层次，有利于培养学生思维的灵活性和广阔性。在教学中，教师要启发学生对条件不确定的题目，可以从结论出发，根据已学过的知识，逐步逆推，寻找使结论成立的条件。

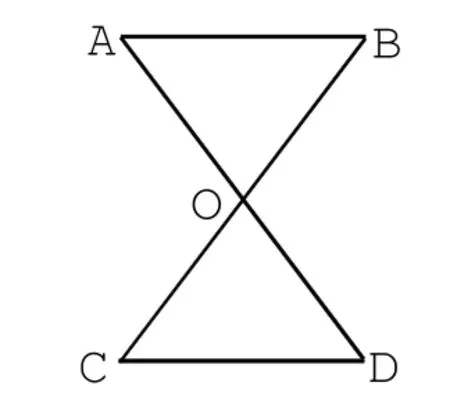
图1

二、对问题的结论进行发散训练

确定了已知条件之后，但是还没有固定的结论，这就可以对问题的结论进行发散训练。让学生更多地探究未知元素，并对这些未知元素进行观察、猜想、推理，得出结论。

例如，已知：如图2，∠ABC=∠DBE=90°，BA=BC，BD=BE，求证：CD=AE。那么，CD与AE还有什么关系？

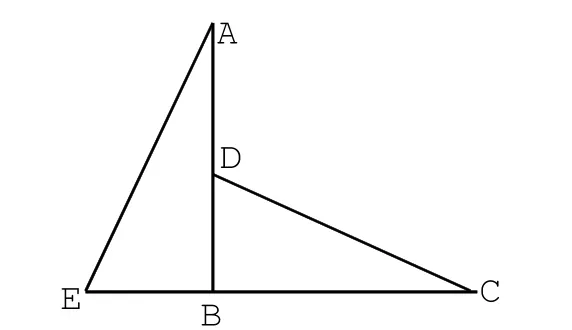
图2

这样既可以充分掌握数学基本知识，又可以了解知识间横向、纵向的联系，有利于培养思维的流畅性和广阔性。在课堂教学过程中，教师要引导学生根据已有的知识、经验，通过观察、猜想、推理，得出结论。

三、对问题的解法进行发散训练

一题多解也就是对问题的解法进行发散，是指同一个问题可以从不同的角度、用不同的方法来解。例如：等腰三角形的性质：“等边对等角”该性质的证明方法就是多种的。不是只有构造全等三角形的这一个方法，可以做底边中线，可以做底边的高，也可以作顶角的平分线来论证该性质。在教学过程中，教师要充分利用学生学过的基础知识和基本技能，启发学生在解题过程中不断探索新的方法，寻找新的解题途径。

四、对题目进行变式训练

“一题多变”，就是对题目进行变式，是将题目引申、变化、发散。对问题间的逻辑关系进行提示，不仅可以反复练习，触类旁通。它们之间的区别与联系还可以根据题目的演变过程来了解。

已知：如图3，如四边形ABCF和DBEG是正方形，连结AE、CD，则AE与CD有什么关系？

若将正方形ABCF顺时针旋转到如图4所示的位置，上述关系是否成立？

若将正方形DBEG顺时针旋转到如图5所示的位置，上述关系是否成立？

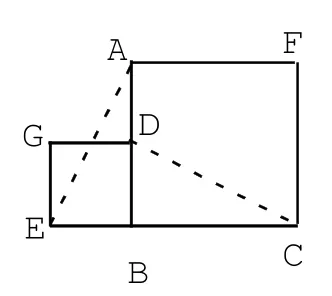
图3

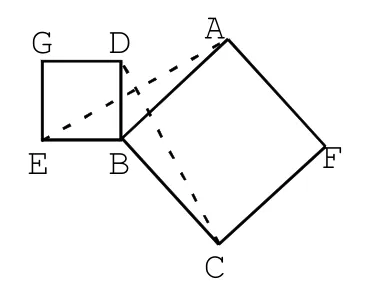
图4

图5

通过这样的训练，可以使学生思维在更大范围、更高层次上发散，有利于学生在流畅、变通的基础上进一步发展思维的独特性。教师要用心启发学生进行纵向与横向的拓展教育，通过解一题，带一片，强化知识的迁移，让学生在一题多变中开阔思路，提高解题能力。

［1］赵海玲.浅谈培养学生数学发散思维能力的策略［J］.中学数学，2012（10）.

［2］张良美.浅析初中数学教学中发散思维的培养［J］.新课程（上），2011（2）.

·编辑 段丽君

翟洪祥（1966—），男，汉族，吉林省辉南县人，就职于吉林省辉南县抚民镇中学。