关于广义量词many的广义三段论推理

李 晟，袁兆隆

(四川师范大学 a.逻辑与信息研究所,b.政治教育学院，成都 610066)

关于广义量词many的广义三段论推理

李 晟a,b，袁兆隆a,b

(四川师范大学 a.逻辑与信息研究所,b.政治教育学院，成都 610066)

三段论在自然语言信息处理和知识推理中占据着突出的地位，它们在自亚里士多德以来的逻辑中也一直扮演着重要作用。我们用广义量词many对传统三段论推理进行了扩展，利用广义量词理论和集合论，从语法上证明了14个广义三段论推理的有效性。这一方法为其他广义量词的广义三段论提供了一个简单合理的数学模式。

传统三段论；广义三段论；广义量词；推理

一 引言

自亚里士多德以来的古代逻辑对直言三段论(categorical syllogisms)、假言三段论(hypothetical syllogisms)、预疑三段论(prosleptic syllogisms)[1]、模态三段论都有所研究。其中，影响最为广泛的是起源于亚里士多德的直言三段论，在直言三段论的基础上，经过哲学家和逻辑学家们的改进和发展，逐渐形成了传统三段论[2]。经过深入研究，一些学者发现大多数自然语言推理不仅仅与传统三段论推理有关，而且还与广义三段论(generalized syllogisms)推理有关[3]。

传统三段论揭示的是一阶逻辑中的标准量词(即全称量词和存在量词)推理性质。在256个传统三段论中，只有24个三段论才是有效的。事实上，在自然语言中，大部分三段论是广义三段论，传统三段论仅仅占一小部分。广义三段论揭示的是广义量词的推理性质。正如广义量词是一阶逻辑中的标准量词的扩展一样，广义三段论是传统三段论的扩展，因此也叫做扩展三段论[4]。正如对传统三段论的有效性加以判断是经典逻辑的重要内容一样，对广义三段论的有效性加以判断则是现代逻辑(尤其是自然语言逻辑，更具体地说是广义量词理论)的重要内容。

对于广义三段论及其有效性的研究，国外学者取得了可喜的成果。比如：Moss(2010)[5]使用动词see或love对传统三段论逻辑进行了扩展，在此基础上，给出了关于{all,some,see}这一英语语言片段的完全性和可靠性证明；Murinová 和Novák(2012)[6]在Peterson(2000)[7]的广义三段论研究的基础上，利用模糊类型论(fuzzy type theory)这一高阶模糊逻辑的知识，从语法上形式化地证明了包括24个有效的传统三段论在内的105个广义三段论的有效性。Endrullis和Moss(2015)[8]124-139研究了关于most这一居间量词(intermediate quantifier)的广义三段论的有效性，并给出了关于{all,some,most}这一英语语言片段的完全性和可靠性证明。

虽然国外学者对广义三段论及其有效性的研究取得了这些成果，但是这些研究都存在着一定的缺憾。比如Murinová 和Novák(2012)[6]利用模糊类型论这一高阶模糊逻辑知识，对广义三段论的证明过程显得繁琐复杂。我们发现利用广义量词理论[9]和集合论的知识，就可以简洁明了地对广义三段论进行形式化及其有效性的证明。这正是本文主旨之所在。

正如广义量词可以包括一阶逻辑中的标准量词一样，广义三段论可以包括传统三段论。在下文中，如果没有特别说明，广义量词都是指包含一阶逻辑中的两个标准量词的广义量词，广义三段论都是指包含传统三段论在内的广义三段论。限于篇幅原因，本文把重点放在自然语言中常见的广义量词many的广义三段论的有效性的探讨上。

二 相关基础知识

广义量词包括：全称量词和存在量词、限定词、以及由a/an、the或其他量化关系指称所形成的所有名词短语。比如，正好三个小孩、你的手、所有的商品、几乎不、没有、两者都不、一打的、不超过五分之三的等，都是广义量词。在自然语言中，最常见的广义量词是〈1〉类型量词和〈1,1〉类型量词，而且“对〈1〉类型量词的研究常常可以转化成对〈1,1〉类型量词的研究”[10]16，因此，〈1,1〉类型量词是广义量词理论研究的重点。在自然语言中，大多数限定词对应的都是〈1,1〉类型广义量词。

下面我们给出本文将用到的广义量词的真值定义。

定义1：常见广义量词的真值定义

(1)all(S,P)⟺S⊆P；

(2)no(S,P)⟺S∩P=Ø；

(3)some(S,P)⟺S∩P≠Ø；

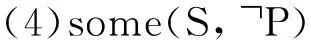
(5)most(S,P)⟺|S∩P|≥0.5|S|；

(7)many(S,P)⟺|S∩P|≥0.6|S|；

(9)almost all(S,P)⟺|S∩P|≥0.9|S|；

根据定义1，直观上，在相同的论域下，我们很容易得到以下事实。

事实0：

(1)的意思是，由“所有的S都是P”，可以推出“大多数S都是P”；(4)的意思是，由“大多数S都不是P”，可以推出“有些S不是P”；其他的意思类似。

证明：(1)假设all(S,P)成立，根据定义1的(1)可知：all(S,P)⟺S⊆P，而|S∩P|=|S|≥0.5|S|，即|S∩P|≥0.5|S|，再根据定义1的(5)“most(S,P)⟺|S∩P|≥0.5|S|”可知：most(S,P)成立。证毕。

(8)的证明与(4)的证明类似，而其他的证明则与(1)的证明类似。

三 关于many的有效的广义三段论推理模式及其证明

在Murinová与Novák(2012)[6]、林胜强和张晓君(2014)[11]、张晓君(2014)[12]等人工作的基础上，我们可给出如下14个关于many的有效的广义三段论推理模式及其证明。

事实1：广义三段论all(M,P) &many(S,M) ⟹many(S,P)是有效的。

证明：假设all(M,P) &many(S,M)这两个前提都成立，那么根据定义1对all和many的真值定义可知：all(M,P)⟺M⊆P，many(S,M)⟺|S∩M|≥0.6|S|。即：M⊆P且|S∩M|≥0.6|S|，因此，|S∩P|≥0.6|S|。再根据many的真值定义可知：many(S,P)成立。证毕。

例如：(1)大前提：所有的苹果都卖完了。

小前提：很多上周进的水果都是苹果。

结论：很多上周进的水果都卖完了。

这一广义三段论实例例证了事实1是有效的。

事实2：广义三段论all(M,P) &many(S,M)⟹most(S,P)是有效的。

证明：根据事实1可知：all(M,P) &many(S,M)⟹many(S,P)，再根据事实0的(11)可知：many(S,P)⟹most(S,P)，因此，all(M,P) &many(S,M)⟹most(S,P)。事实2得证。

事实3：广义三段论all(M,P) &many(S,M)⟹some(S,P)是有效的。

根据事实1和事实0的(7)可以直接证得事实3。

事实4：广义三段论all(M,P) &almost all(S,M)⟹many(S,P)是有效的。

证明：假设all(M,P) &almost all(S,M)这两个前提都成立，那么根据定义1对all和almost all的真值定义可知：all(M,P)⟺M⊆P，almost all (S,M)⟺|S∩M|≥0.9|S|。即：M⊆P且|S∩M|≥0.9|S|，因此，|S∩P|≥0.9|S|。再根据almost all的真值定义可知：almost all (S,P)成立。再根据事实0的(9)“almost all(S,P)⟹many(S,P)”可知：many(S,P)成立。证毕。

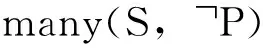
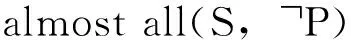
事实6的证明与事实5的证明类似。

例如：(2)大前提：所有的山西人都习惯把多年积攒的钱财留给儿女。

小前提：在成都打工的人中没有人习惯把多年积攒的钱财留给儿女。

结论：在成都打工的人中很多人都不是山西人。

这一广义三段论实例例证了事实7是有效的。

事实8的证明与事实7的证明类似。

例如：(3)大前提：所有在市中心买写字楼的人都是本地人。

小前提：很多做药材生意的人都不是本地人。

结论：很多做药材生意的人都没有在市中心买写字楼。

这一广义三段论实例例证了事实9是有效的。

根据事实9和事实0的(12)可以证明事实10。

事实11的证明与事实5的类似。

根据事实11和事实0的(12)可以直接证得事实12。

事实13的证明与事实5的类似。

四 结论

通过仔细观察上述14个关于many的有效的广义三段论推理模式，就会发现：这些有效的三段论在前提中要么包含all这样的全称肯定命题(事实1-4、事实7-10、事实14这9个事实就是如此)，要么包含no这样的全称否定命题(事实5-8、事实10-13、事实14这9个事实就是如此)，要么二者兼之(事实7、事实8和事实14这3个事实就是如此)。这一规律与传统三段论的规律是吻合的，即：当肯定或否定一类对象的全部时，也就肯定或否定了这类对象中的部分。这一规律对于其他广义量词(比如most、few、at lest half of the、almost all等)是否也成立呢？虽然我们还不能够对此断然下结论，但是这一规律将为我们寻找关于其他广义量词的有效的广义三段论，还是有很大的启迪作用的。

事实上，利用本文的研究方法，还可以研究由两个及其以上的广义三段论嵌套而成的语篇推理的有效性。例如：“所有的苹果都卖完了，很多上周进的水果都是苹果，所以很多上周进的水果都卖完了。上周进的所有水果都是从城北批发市场进的，所以很多上周从城北批发市场进的水果都卖完了。”这一语篇推理其实是有两个广义三段论组成，而且第一个三段论的结论是第二个三段论的大前提。

总之，本文充分利用了包含〈1,1〉类型广义量词的语句可表示成Q(S,P)这样的三分结构，以及这类量词的真值定义和简单的集合论知识，对广义三段论进行了简洁明了的形式化表示和证明。自然语言中〈1,1〉类型广义量词非常多，而利用本文的研究方法，就可以对其他广义量词的广义三段论进行形式化，以及对它们有效性进行证明。因此，本文的研究方法具有很大的普适性和广泛的应用价值，尤其是对自然语言信息处理和计算机科学中的知识表示和知识推理而言更是如此，而且这些研究也将推动广义量词理论向纵深方向发展。

[1]BOBZIEN S.Ancient Logic[EB/OL].[2016-01-26].http://plato.stanford.edu/entries /logic-ancient,2015.

[2]余维发.亚里士多德三段论与其他传统三段论之区别[J].哈尔滨学院学报,2006，(9):23-26.

[3]郝一江.自然语言语篇推理的形式化探究[J].湖南科技大学学报(社会科学版),2016，(1):33-37.

[4]张晓君,林胜强.如何利用广义量词的语义性质判断扩展三段论的有效性[J].逻辑学研究，2013，(2):42-56.

[5]MOSS L.S.Syllogistic logics with verbs[J].Journal of Logic and Computation,2010,20(4):947-967.

[7]PETERSON P.Intermediate Quantifiers: Logic,Linguistics,and Aristotlian Semantics[M].Aldershot：Ashgate,2010.

[8]ENDRULLIS J,MOSSL S.Syllogistic logic with “Most”[C]//V.de Paiva et al.(eds.).Logic,Language,Information,and Computation,Volume 9160 of the series Lecture Notes in Computer Science.2015.

[9]PETERS S,WESTERSTHL D.Quantifiers in Language and Logic[M].Oxford: Claredon Press,2006.

[10]林胜强.广义量词的现代对当方阵研究[J].四川师范大学学报(社会科学版),2015,(1):15-20.

[11]林胜强,张晓君.广义量词的推理模式研究[J].湖南科技大学学报(社会科学版),2014,(6):29-33。

[12]张晓君.广义量词理论研究[M].厦门：厦门大学出版社，2014.

[责任编辑：帅 巍]

Generalized Syllogistic Reasoning Including the Generalized Quantifier “many”

LI Shenga,b,YUAN Zhao-longa,b

(a.Institute of Logic and Information,b.College of Political Education,Sichuan Normal University,Chengdu,Sichuan 610066,China)

Syllogistic arguments are prominent in natural language information processing and knowledge reasoning,and they have played important role in logic since Aristotle .The generalized quantifier “many” is applied in this paper to expand the traditional reasoning of generalized syllogisms,and the validity of 14 generalized syllogisms is syntactically proved by means of generalized quantifier theory and set theory.This method provides a simple and reasonable mathematical model of generalized syllogisms for other generalized quantifiers.

classical syllogisms;generalized syllogisms;generalized quantifiers;reasoning

2016-03-06

国家社科基金西部项目“面向中文信息处理的汉语主谓句的逻辑语义及其推理模式研究”(15XYY012)。

李晟(1986—)，男，四川德阳人，逻辑学博士，四川师范大学逻辑与信息研究所研究员，主要研究现代逻辑、自然语言逻辑等；

袁兆隆(1992—)，男，广东中山人，四川师范大学政治教育学院硕士研究生，主要研究现代逻辑和自然语言逻辑。

B812.23

A

1000-5315(2017)01-0015-05