A BIFURCATION PROBLEM ASSOCIATED TO AN ASYMPTOTICALLY LINEAR FUNCTION∗
Soumaya SˆAANOUNI
Department of Mathematics,Faculty of Sciences of Tunis,University of Tunis El Manar, Campus University 2092 Tunis,Tunisia
Nihed TRABELSI
Higher Institut of Medicals Technologies of Tunis,University of Tunis El Manar, 9 Street Dr.Zouhair Essaf1006 Tunis,Tunisia
A BIFURCATION PROBLEM ASSOCIATED TO AN ASYMPTOTICALLY LINEAR FUNCTION∗
Soumaya SˆAANOUNI
Department of Mathematics,Faculty of Sciences of Tunis,University of Tunis El Manar, Campus University 2092 Tunis,Tunisia
E-mail:saanouni.soumaya@yahoo.com
Nihed TRABELSI
Higher Institut of Medicals Technologies of Tunis,University of Tunis El Manar, 9 Street Dr.Zouhair Essaf1006 Tunis,Tunisia
E-mail:nihed.trabelsi78@gmail.com
We study the existence of positive solutions to a two-order semilinear elliptic problem with Dirichlet boundary condition
extremal solution;regularity;bifurcation;stability
2010 MR Subject Classifcation35B65;34D35;70K50
1 Introduction and Statement of Main Results
The main interest of non-linear physics lies in its ability to explain the evolution of the problems:a phenomenon usually depends on a number of parameters,called control parameters that control the evolution of the system.By variation of the parameters and the result of nonlinearities,the system may undergo transitions.In math,they are bifurcations.
In biology;population dynamics,the equations of reactions-difusion were proposed by Turing(1952)for modeling morphogenesis phenomena.A model of interaction of species or chemicals is given by the diferential equations

where u represents the density,div(c∇u)represents the substance of difusion through the system,and f models the interaction of substances.Moreover the broadcast functions c and the terms of reactions f may depend on(x,t)and the concentrations u it as a nonlinearity way.
In case where c and t are constants,various authors have studied the existence of weak solutions for the bifurcation problem

where Ω is a bounded open subset of Rn,n≥2.
Mironescu and R˘adulescu proved in[13,14]that there exists 0<λ∗<∞,a critical value of the parameter λ,such that(Eλ)has a minimal,positive,classical solution uλfor 0<λ<λ∗and does not have a weak solution for λ>λ∗.
Our main interest here will be in the study of a bifurcation problem for λ>0
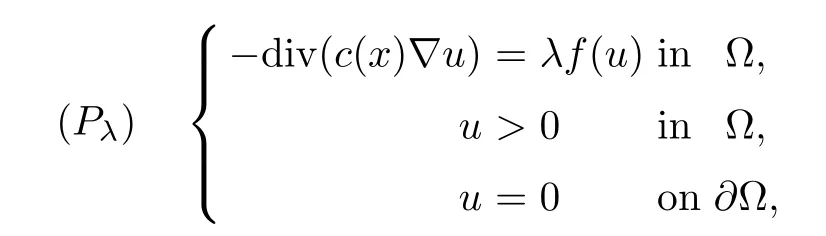
which is a generalization of(Eλ).Where Ω be a smooth bounded domain in Rn(n≥2),c(x) is a smooth bounded positive function onis a positive,increasing and convex smooth function,such that
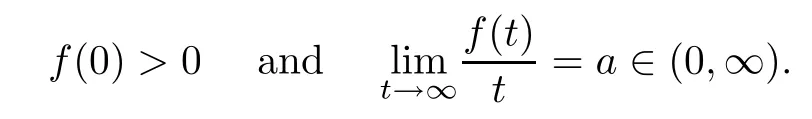
The value a was be crucial in the study of(Eλ∗)and of the behavior of uλwhen λ tends to λ∗.
Throughout the paper,we denote by k·k2,the L2(Ω)-norm,whereas we denote by k·k, the H10(Ω)-norm given by
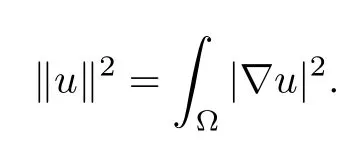
We say that u∈H10(Ω)is a weak solution of the problem(Pλ),if f(u)∈L1(Ω)and

Such solutions are usually known as weak energy solutions.For short,we will refer to them simply as solutions wish is assuredly by the next lemma.
Lemma 1.1Since f(t)≤at+f(0),if u∈L1(Ω)is a weak solution of(Pλ),it is easily seen by a standard bootstrap argument that u is always a classical solution.
In the rest of this paper,we denote by a solution of problem(Pλ)any weak or classical solution.
Defnition 1.2We say that a solution uλof problem(Pλ)is minimal if uλ≤u in Ω for any solution u of(Pλ).
Defnition 1.3We say that u∈H10(Ω)is a supersolution of(Pλ)if f(u)∈L1(Ω)and
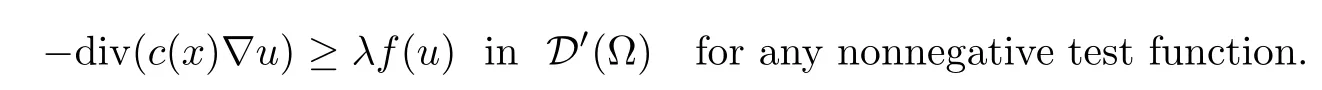
Reversing the inequality one defnes the notion of subsolution.
Defnition 1.4A solution u of problem(Pλ)is stable if and only if the frst eigenvalue of the linearized operator

given by
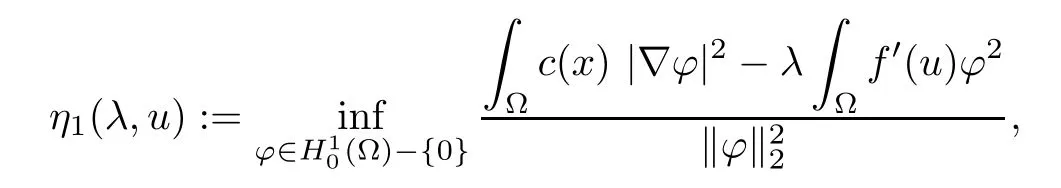
is nonnegative.
If η1(λ,u)<0,the solution u is said to be unstable.
Let v1be a positive eigenfunction associated with the frst eigenvalue λ1of the operator−div(c(x)∇)with Dirichlet boundary conditions,namely,

Next,we let
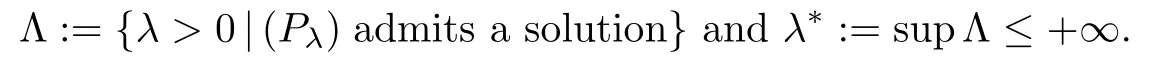
We also let
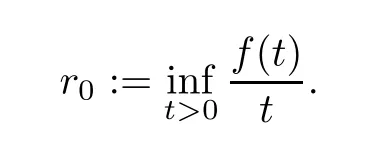
The two values a and r0that we have already defned will be important in the bifurcation phenomena.More precisely,in the frame of the critical value λ∗.
In this article,we want to show the following three theorems
Theorem 1.5There exists a critical value λ∗∈(0,∞)such that the following properties hold true
(i)for any λ∈(0,λ∗),problem(Pλ)has a minimal solution uλ,which is the unique stable solution of(Pλ);
(ii)for any λ∈(0,λ1/a),uλis the unique solution of problem(Pλ);
(iii)the mapping λ 7→uλis increasing;
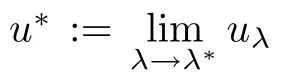
An important role in our arguments will be played by

We distinguish two diferent situations strongly depending on the sign of l.
Theorem 1.6Assume that l≥0.Then
(i)λ∗=λ1/a;
(ii)problem(Pλ∗)has no solution;
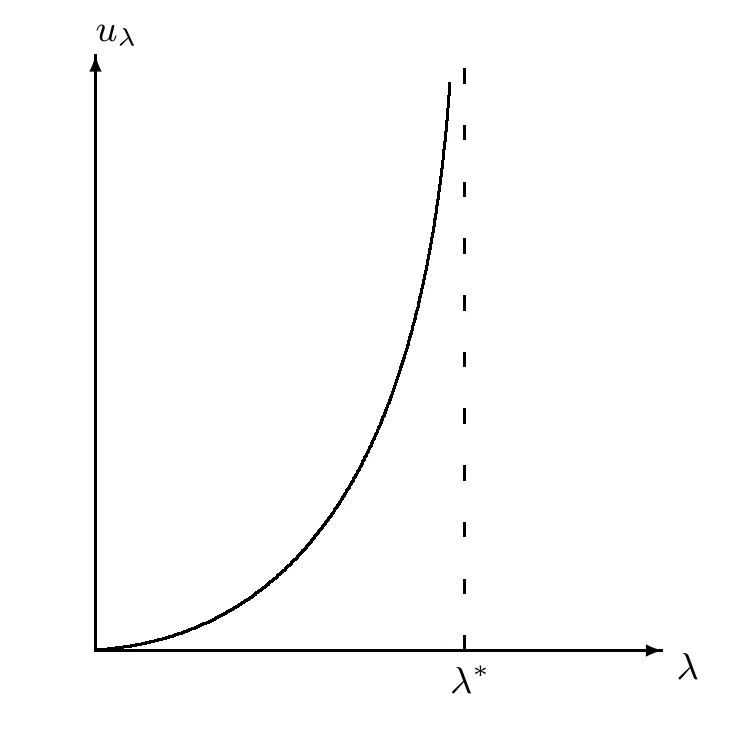
Fig.1 Behavior of the minimal solution
Theorem 1.7Assume that l<0.Then the critical value λ∗belongs to(λ1/a,λ1/r0) and(Pλ∗)has a unique solution u∗.In this case,problem(Pλ)has an unstable solution vλfor any λ∈(λ1/a,λ∗)and the sequence(vλ)λhas the following properties:
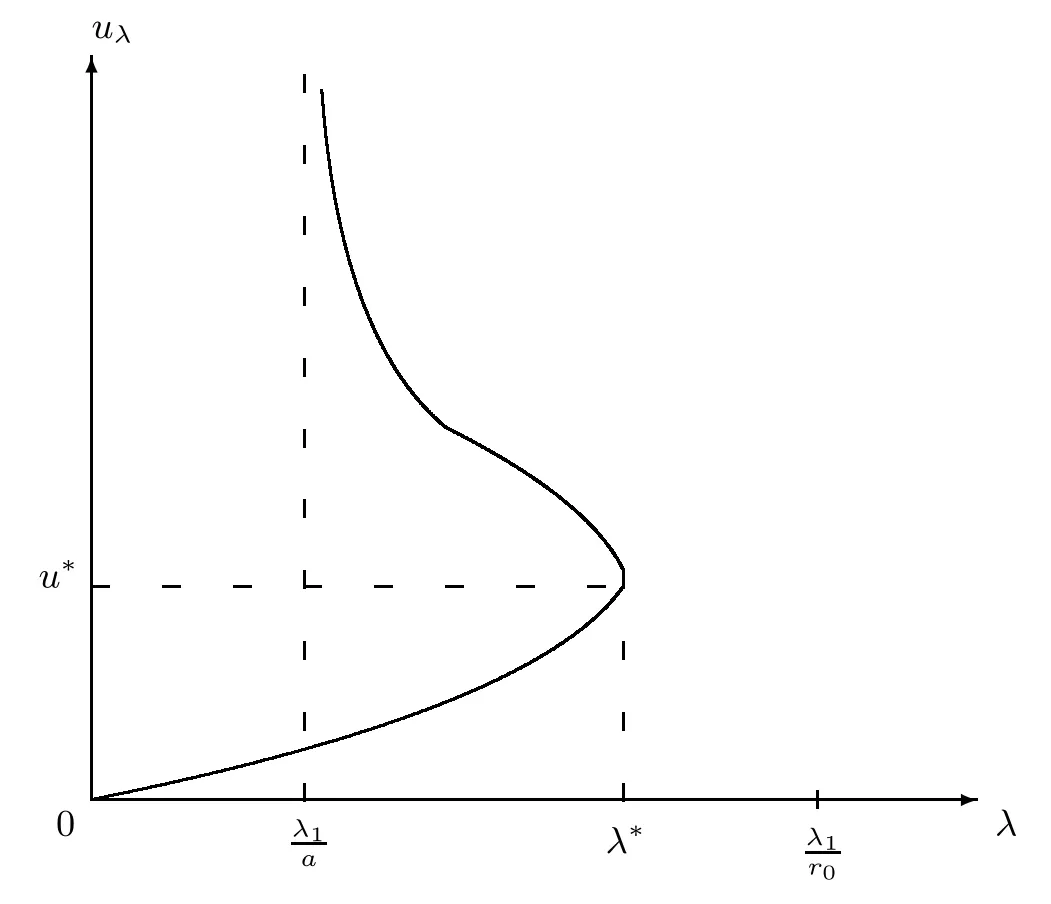
Fig.2 Bifurcation branches in the case l<0
2 Proof of Theorem 1.5
The frst part of this article is conserved to prove Theorem 1.5,when the existence of the critical value λ∗is a consequence of the following auxiliary result.
Lemma 2.1Problem(Pλ)has no solution for any λ>λ1/r0,but has at least one solution provided λ is positive and small enough.
ProofTo show that(Pλ)has a solution,we use the barrier method.To this aim,letwhich satisfes
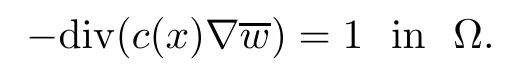
The choice of w implies that w is a super-solution of(Pλ)for λ≤1/f(kwk∞).
Notice that for any λ>0,the function w≡0 is a sub-solution of(Pλ)since f(0)>0.
Next,we defne a sequence wn∈H2(Ω)by

The maximum principle(see[5])implies that
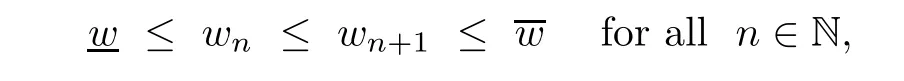
so that the sequence(wn)n≥0is increasing and bounded,then it converges.It follows that problem(Pλ)has a solution.
Assume now that u is a solution of(Pλ)for some λ>0.Using v1given in(1.1)as a test function and integrating by parts,we get

This yields

Since v1>0 and u>0,we conclude that the parameter λ should belong to(0,λ1/r0).This completes our proof.
Another useful result is stated in what follows.
Lemma 2.2Assume that problem(Pλ)has a solution for some λ∈(0,λ∗).Then there exists a minimal solution denoted by uλ.Moreover,for any λ′∈(0,λ),problem(Pλ′)has a solution.
ProofFix λ∈(0,λ∗)and let u be a solution of(Pλ).As above,we use the barrier method to obtain a minimal solution of(Pλ).The basic idea is to prove by induction that the sequence(wn)n≥0defned in(2.1)is increasing and bounded by u,so it converges to some solution uλ.Since uλis independent of the choice of u,then it is a minimal solution.
Now,if u is a solution of(Pλ),then u is a super-solution for problem(Pλ′)for any λ′in (0,λ)and 0 can be used always as a sub-solution.These complete the proof.
Remark 2.3Thanks to Lemmas 2.1 and 2.2,the set Λ is an interval not empty and bounded.
Proof of(i)of Theorem 1.5First,we claim that uλis stable.Indeed,arguing by contradiction,i.e.,the frst eigenvalue η1(λ,uλ)is negative.Then,there exists an eigenfunction ψ∈H2(Ω)such that

Consider uε:=uλ−εψ.Hence,by linearity,we have

Since η1(λ,uλ)<0,for ε>0 small enough,we have

Then,for ε>0 small enough,we use the strong maximum principle(Hopf’s lemma,see[9]) to deduce that uε≥0 is a super-solution of(Pλ).As before,we obtain a solution u such that u≤uεand since uε Now,we show that(Pλ)has at most one stable solution.Assume the existence of another stable solution v 6=uλof problem(Pλ).Then the function w:=v−uλ>0 satisfes Therefore Thanks to the convexity of f,the term in the brackets is nonpositive,hence which implies that f is afne over[uλ,v]in Ω.So,there exists two real numbers¯a and b such that Finally,since uλand v are two solutions to−div(c(x)∇w)=λ¯aw+λb,we obtain that This is impossible since b=f(0)>0 and w=v−uλis positive in Ω. which shows that Impossible for λ∈(0,λ1/a).So,η1(λ,u)≥0 and by(i),we obtain the uniqueness of u. For the existence,we consider the minimization problem where with If λ∈(0,λ1/a),there exist ε>0 and A>0 depending on λ such that Standard arguments imply that J(u)is coercive,bounded from below and weakly lower semi-continuous in H10(Ω).Hence,the minimum of J is attained by some function u∈H10(Ω) and also by u+since J(u+)≤J(u).So,the critical point u of J gives a solution of(Pλ). Proof of(iii)of Theorem 1.5By sub-and super-solution method,see Lemma 2.2 we obtain that the mapping λ 7−→uλis increasing and this proves(iii). Proof of(iv)of Theorem 1.5Consider the nonlinear operator where α∈(0,1)and E is the function space defned by Remark 2.4Thanks to Lemma 2.1 and(ii)of Theorem 1.5,the critical value λ∗satisfes To prove this theorem,we can assume that c(x)≥1,we show that the three assertions are equivalent.And fnally,we prove that one is true. We frst recall the following result which is due to H¨ormander[10]. Lemma 3.1Let Ω be an open bounded subset of Rn,n≥2 with smooth boundary.Let (un)be a sequence of super-harmonic nonnegative functions defned on Ω.Then the following alternative holds: (ii)or(un)contains a subsequence which converges into some function u. Remark 3.2The result of H¨ormander is also true if(un)is a sequence of a superbiharmonic nonnegative functions. First,we assume that λ∗=λ1/a.If(Pλ∗)has a solution u∗,then as we have already observed in(iv)of Theorem 1.5 η1(λ∗,u∗)=0.Thus,there exists ψ∈H2(Ω)satisfying Using v1,given in(1.1),as a test function and integrating by parts,we obtain therefore Since λ1−λ∗f′(u∗)≥0,the above equation forces λ1−λ∗f′(u∗)=0.Hence If not,Using v1and integrating by parts,we have then i.e., Hence,problem(Pλ∗)has no solution and(i)implies(ii). with Since f(t)≤at+f(0)and c(x)≥1,we have where cλis a positive constant independent on λ. Moreover,by the trace theorem, We deduce that Moreover,it simply shows that(ii)and(iii)are equivalent. Then,up to a subsequence,we obtain Moreover, and Then, Multiplying by v1,which is defned in(1.1),we obtain This proves(i). To fnish the proof of Theorem 1.6,we need only to show that(Pλ1/a)has no solution. Indeed,assume that u is a solution of(Pλ1/a).Since f(t)−at≥0,we have Multiplying the previous equation by v1and integrating by parts,we get f(u)=au in Ω,which contradicts f(0)>0.This concludes the proof of Theorem 1.6. Remark 3.3Observe that the equivalence of the assertions of Theorem 1.6 does not depend on the sign of l. For the frst part of Theorem 1.7,we have already seen in Remark 2.4 that λ1/a≤λ∗≤λ1/r0.Hence it sufces to prove that λ∗6=λ1/a and λ∗6=λ1/r0. First,assume that λ∗=λ1/a.Let uλbe the minimal solution to(Pλ).Then,multiplying (Pλ)by v1given in(1.1)and integrating,we obtain Passing to the limit in the last inequality as λ tends to λ∗,we fnd which is impossible. Now,assume that λ∗=λ1/r0and let u be a solution of problem(Pλ∗).Multiplying(Pλ∗) by v1and integrating by parts,we have Recall that η1(λ∗,u∗)=0,so let ψ be the corresponding eigenfunction.Multiplying the last inequality by ψ and integrating by parts,we fnd Therefore,we must have equalityin Ω,which implies that f is linear inand this leads a contradiction as in the proof of Theorem 1.6. The second part of Theorem 1.7 concerning the existence of a non stable solution vλof (Pλ)will be proved by using the mountain pass theorem of Ambrosetti and Rabinowitz[2]in the following form. Theorem 4.1Let E be a real Banach space and J∈C1(E,R).Assume that J satisfes the Palais-Smale condition and the following geometric assumptions: (∗)there exist positive constants R and ρ such that (∗∗)there exists v0∈E such that kv0−u0k>R and J(v0)≤J(u0). Then the functional J possesses at least a critical point.The critical value is characterized by where and satisfes In our case, where E is the function space defned in(2.2)and We take u0as the stable solution uλfor each λ∈(λ1/a,λ∗). Remark 4.2The energy functional J belongs to C1(E,R)and Since η1(λ,uλ)≥0,the function uλis a local minimum for J,and in order to transform it into a local strict minimum,we apply the mountain pass theorem not for J,but to the perturbed functional Jεdefned by for all ε∈[0,ε0],where We observe that Jεis also in C1(E,R)and Using the same arguments of Mironescu and R˘adulescu in[14,Lemma 9],we show in the next lemma that Jεsatisfes the Palais-Smale compactness condition. Lemma 4.3Let(un)⊂E be a Palais-Smale sequence,that is, Then(un)is relatively compact in E. ProofSince any subsequence of(un)verifes(4.1)and(4.2)it is enough to prove that (un)contains a convergent subsequence.It sufces to prove that(un)contains a bounded subsequence in E.Indeed,suppose we have proved this.Then,up to a subsequence,un−→u weakly in E,strongly in L2(Ω).Now(4.2)gives that Note that f(un)−→f(u)in L2(Ω)because|f(un)−f(u)|≤a|un−u|.This shows that That is The above equality multiplied by u gives Now(4.2)multiplied by(un)gives in view of the boundedness of(un)and the L2(Ω)-convergence of unand f(un),we have and Hence,(4.3)and(4.4)gives which insures us that un−→ u in E.Actually,it is enough to prove that(un)is(up to a subsequence)bounded in L2(Ω).Indeed,the L2(Ω)-boundedness of(un)implies that E-boundedness of(un)as it can be seen by examining(4.1). We shall conclude the proof obtaining a contradiction from the supposition that kunk2→∞.Let un=knwnwith kn>0,kn−→∞and kwnk2=1.Then which can still write as follows However,since|f(t)|≤a|t|+b,we have This shows that We claim that Indeed,(4.2)divided by kngives for each v∈E.Now Hence(4.5)can be concluded from(4.6)if we show that 1/knf(un)converges(up to a subsequence)to a w+in L2(Ω).Now 1/knf(un)=1/knf(knwn)and it is easy to see that the required limit is equal to a w in the set{x∈Ω:wn(x)−→w(x)6=0}. If w(x)=0 and wn(x)−→w(x),let ε>0 and n0be such that|wn(x)|<ε for n≥n0. Then that is the required limit is 0.Thus,f(un)/kn→a w+a.e.Here b=f(0).Now wn→w in L2(Ω)and,thus,up to a subsequence,wnis dominated in L2(Ω)(see theorem IV.9 in[5]). Since 1/knf(un)≤a|wn|+1/knb,it follows that 1/knf(un)is also dominated.Hence(4.5) is now obtained.Now(4.5)and the maximum principle imply w≥0 and(4.5)becomes Since u−uλis not harmonic,we can choose and this makes uλbecomes a strict local minimal for Jε,which proves(∗). Hence This yields,using the defnition of v1mentioned in(1.1), since kv1k2=1,then we have which implies that, Therefore So,there exists v0∈E such that and(∗∗)is proved.Finally,for all ε∈[0,ε0],let vε(respectively,cε)be the critical point (respectively,critical value)of Jε. Remark 4.4The fact that Jεincreases with ε implies that for all ε∈[0,ε0],cε∈[c0,cε0[. Then,cεis uniformly bounded.Thus,for all ε∈[0,ε0],the critical point vεsatisfes kvε−uλk≥R. Recall that for any ε∈[0,ε0],the function vεbelongs to E and satisfes and Thanks to Lemma 4.3,Remark 4.4,(4.8)and(4.9),there exists v∈E such that satisfying From Remark 4.4,we see that v 6=uλ,which can be also proved using the same arguments of Mironescu and R˘adulescu in[14]. Indeed,note that vεis a solution to(4.8)which is diferent from the unique stable solution uλ.Then,vεis unstable,that is, since(4.8)can be written as where gεis convex,positive and hεis positive.Thus,if(4.10)has solutions satisfying vε= 0 in∂Ω,then it has a minimal one,say wε,which is stable.Now,thanks to Theorem 1.5,all other solutions vεof(4.10)are unstable. The next lemma states that the limit of a sequence of unstable solutions is also unstable (the proof is similar to that of Lemma 11 in[14]). Lemma 4.5Let un⇀ u in H10(Ω)andµn→ µbe such that η1(µn,un)<0.Then, η1(µ,u)<0. ProofThe fact that η1(µn,un)<0 is equivalent to the existence of a ϕn∈H10(Ω)such that Z Since f′≤a,(4.11)shows that(ϕn)is bounded in H10(Ω). Let ϕ∈E be such that,up to a subsequence,ϕn⇀ϕ in H10(Ω).Then This can be seen by extracting from(ϕn)a subsequence dominated in L2(Ω)as in Theorem IV.9 in[5].Now we have Z fnally,since kϕk2=1,we get Obviously,the fact that the function v belongs to C2(¯Ω)∩E follows from a bootstrap argument. Proof of(i)of Theorem 1.7Thanks to Lemma 3.1,if(i)does not occur,then there is a sequence of positives scalars(µn)and a sequence(vn)of unstable solutions to(Pµn)such that vn→v infor some function v. We frst claim that(vn)cannot be bounded in E.Otherwise,let w∈E be such that,up to a subsequence, Therefore, and which implies that−div(c(x)∇w)=λ1af(w)in Ω.It follows that w∈E and solves(Pλ1/a). From Lemma 4.5,we deduce that Relation(4.12)shows that w 6=uλ1/awhich contradicts the fact that(Pλ1/a)has a unique solution.Now,since−div(c(x)∇vn)=µnf(vn),the unboundedness of(vn)in E implies that this sequence is unbounded in L2(Ω),too.To see this,let Then So,we have convergence also in the sense of distributions and(wn)is seen to be bounded in E with standard arguments.We obtain The desired contradiction is obtained since w∈E. Proof of(ii)of Theorem 1.7As before,it is enough to prove the L2(Ω)boundedness of vλnear λ∗and to use the uniqueness property of u∗.Assume that kvnk2→∞asµn→λ∗, where vnis a solution to(Pµn).We write again vn=lnwn.Then, The fact that the right-hand side of(4.13)is bounded in L2(Ω)implies that(wn)is bounded in E.Let(wn)be such that(up to a subsequence) A computation already done shows that which forces λ∗to be λ1/a.This contradiction concludes the proof. [1]Abid I,Jleli M,Trabelsi N.Weak solutions of quasilinear biharmonic problems with positive,increasing and convex nonlinearities.Anal Appl,2008,6(3):213–227 [2]Ambrosetti A,Rabinowitz P.Dual variational methods in critical point theory and applications.J Funct Anal,1973,14:349–381 [3]Arioli G,Gazzola F,Grunau H C,Mitidieri E.A semilinear fourth order elliptic problem with exponential nonlinearity.SIAM J Math Anal,2005,36(4):1226–1258 [4]Branson T.Group representations arising from Lorentz conformal geometry.J Funct Anal,1987,74:199–293 [5]Brezis H.Analyse Fonctionnelle.Th´eorie et Applications.Paris:Masson,1992 [6]Brezis H,Cazenave T,Martel Y,Ramiandrisoa A.Blow up for ut−∆u=g(u)revisited.Adv DifEq, 1996,1:73–90 [7]Filippakis M,Papageorgiou N.Multiple solutions for nonlinear elliptic problems with a discontinuous nonlinearity.Anal Appl,2006,4:1–18 [8]Ghergu M,R˘adulescu V.Singular Elliptic Problems.Bifurcation and Asymptotic Analysis.Oxford Lecture Series in Mathematics and its Applications,Vol 37.Oxford University Press,2008 [9]Gilbarg D,Trudinger N.Elliptic Partial Diferential Equations of Second Order.Heidelberg:Springer-Verlag,2001 [10]H¨ormander L.The Analysis of Linear Diferential Operators I.Berlin:Springer-Verlag,1983 [11]Kielh¨ofer H.Bifurcation Theory.An Introduction with Applications to Partial Diferential Equations. Berlin:Springer-Verlag,2003 [12]Martel Y.Uniqueness of weak solution for nonlinear elliptic problems.Houston J Math,1997,23:161–168 [13]Mironescu P,R˘adulescu V.A bifurcation problem associated to a convex,asymtotically linear function.C R Acad Sci Paris Ser I,1993,316:667–672 [14]Mironescu P,R˘adulescu V.The study of a bifurcation problem associated to an asymtotically linear function.Nonlinear Anal,1996,26:857–875 [15]R˘adulescu V.Qualitative Analysis of Nonlinear Elliptic Partial Diferential Equations.Contemporary Mathematics and Applications,Vol 6.Hindawi Publ Corp,2008 [16]Sanch´on M.Boundedness of the extremal solution of some p-Laplacian problems.Nonlinear Anal,2007, 67(1):281–294 [17]Wei J.Asymptotic behavior of a nonlinear fourth order eigenvalue problem.Comm Partial Difer Equ, 1996,21(9/10):1451–1467 ∗Received May 27,2015;revised April 25,2016. where Ω⊂Rn;n≥2 is a smooth bounded domain;f is a positive,increasing and convex source term and c(x)is a smooth bounded positive function on Ω.We also prove the existence of critical value and claim the uniqueness of extremal solutions.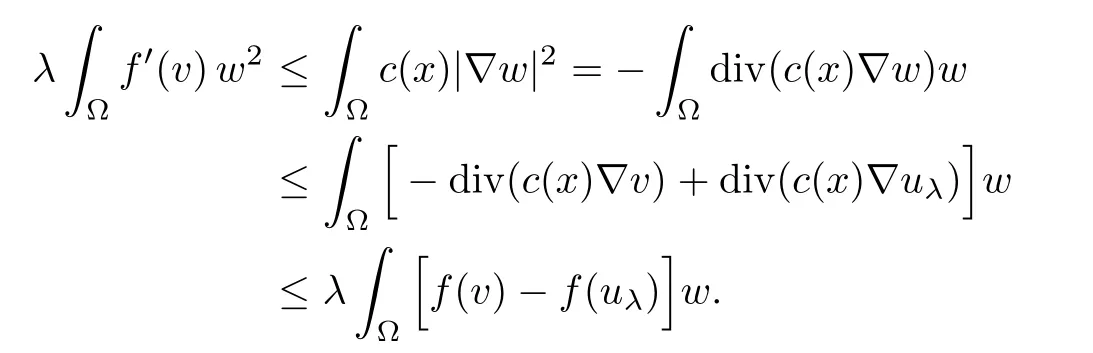
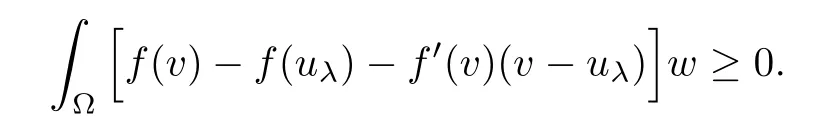
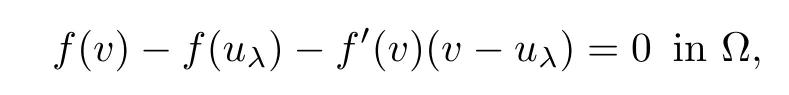
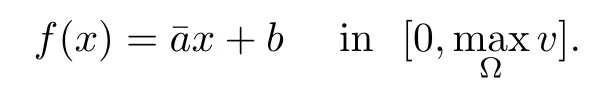


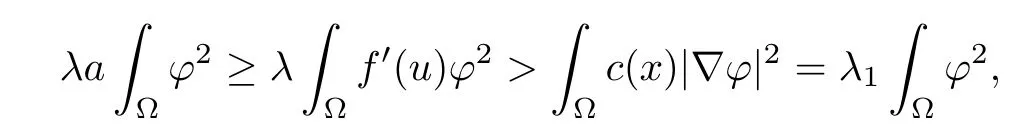

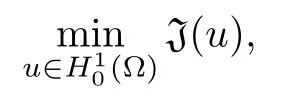



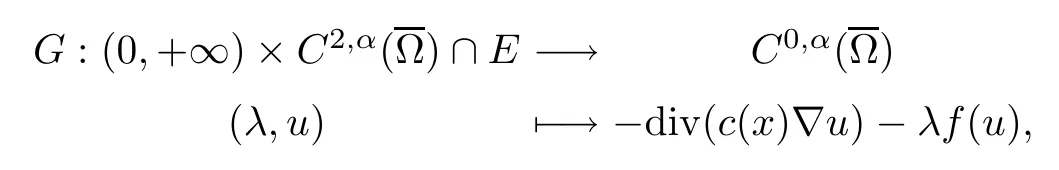

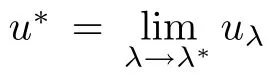

3 Proof of Theorem 1.6


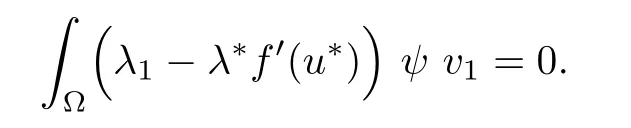
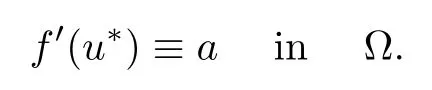
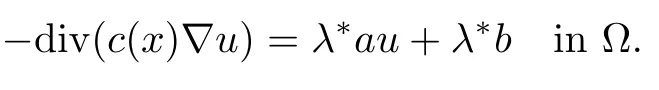
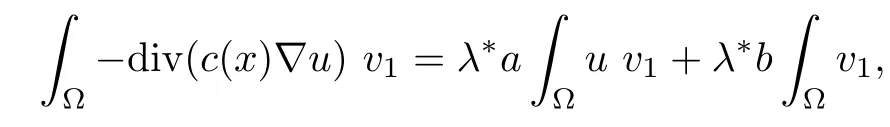
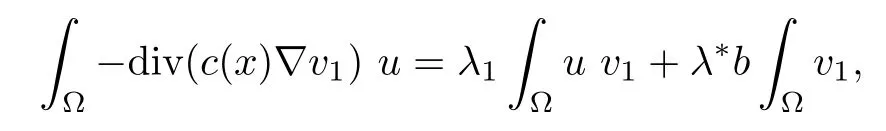
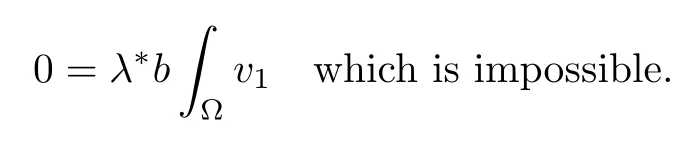
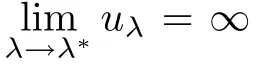
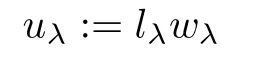

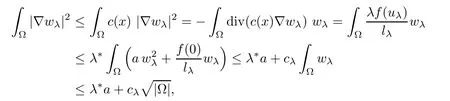

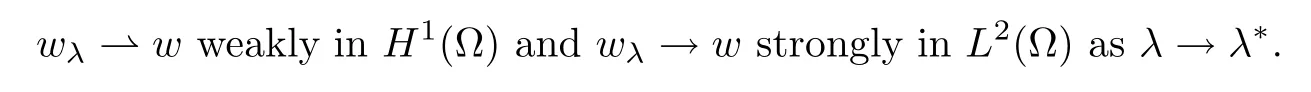


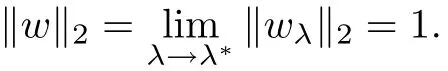

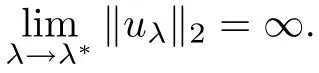

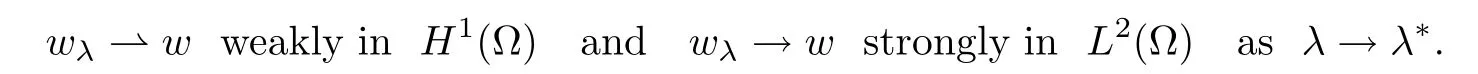
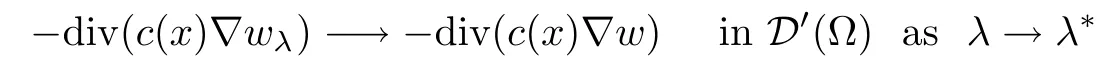


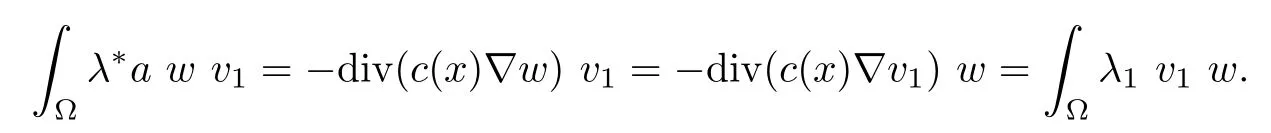

4 Proof of Theorem 1.7
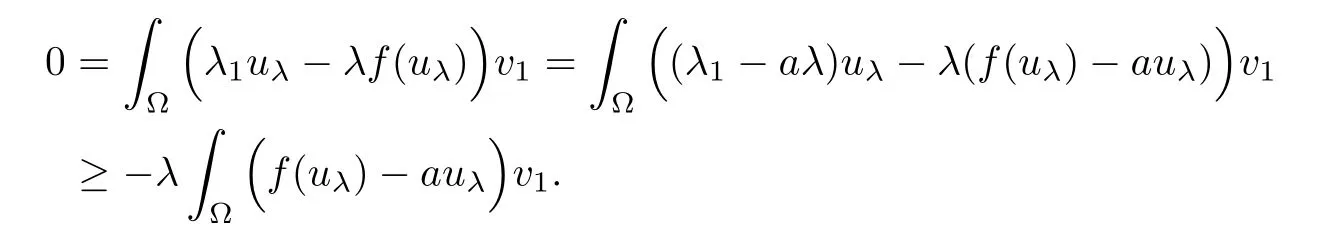
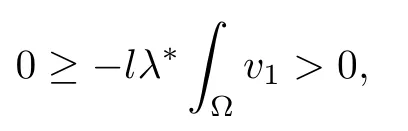
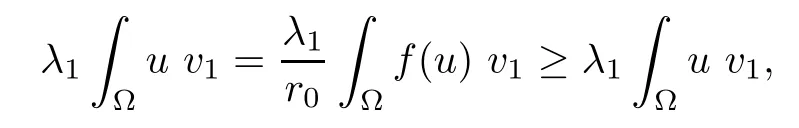

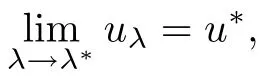





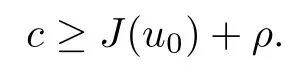
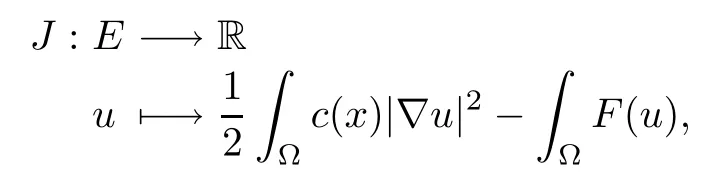
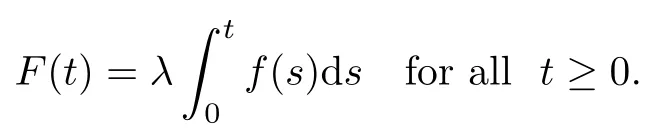
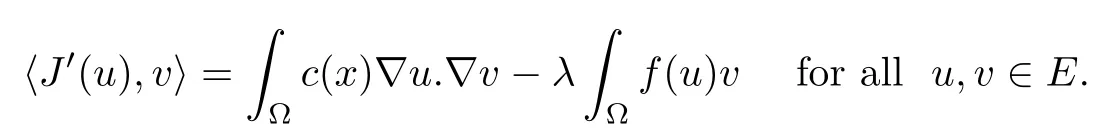

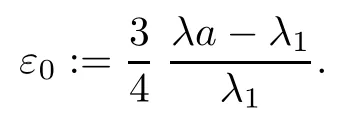
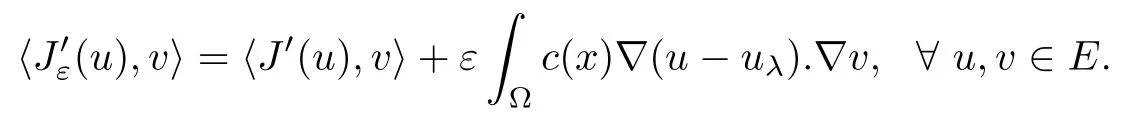

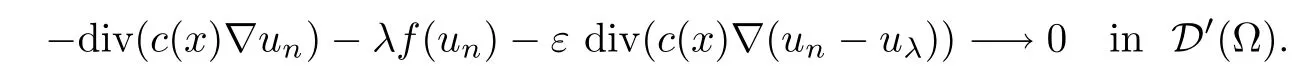

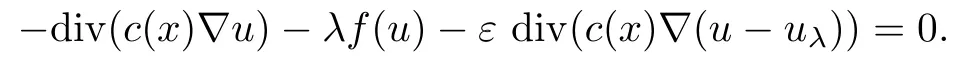


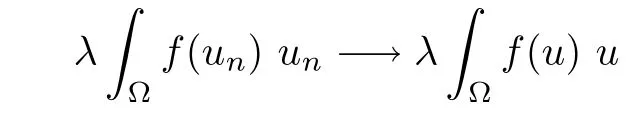
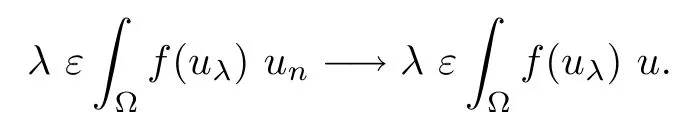

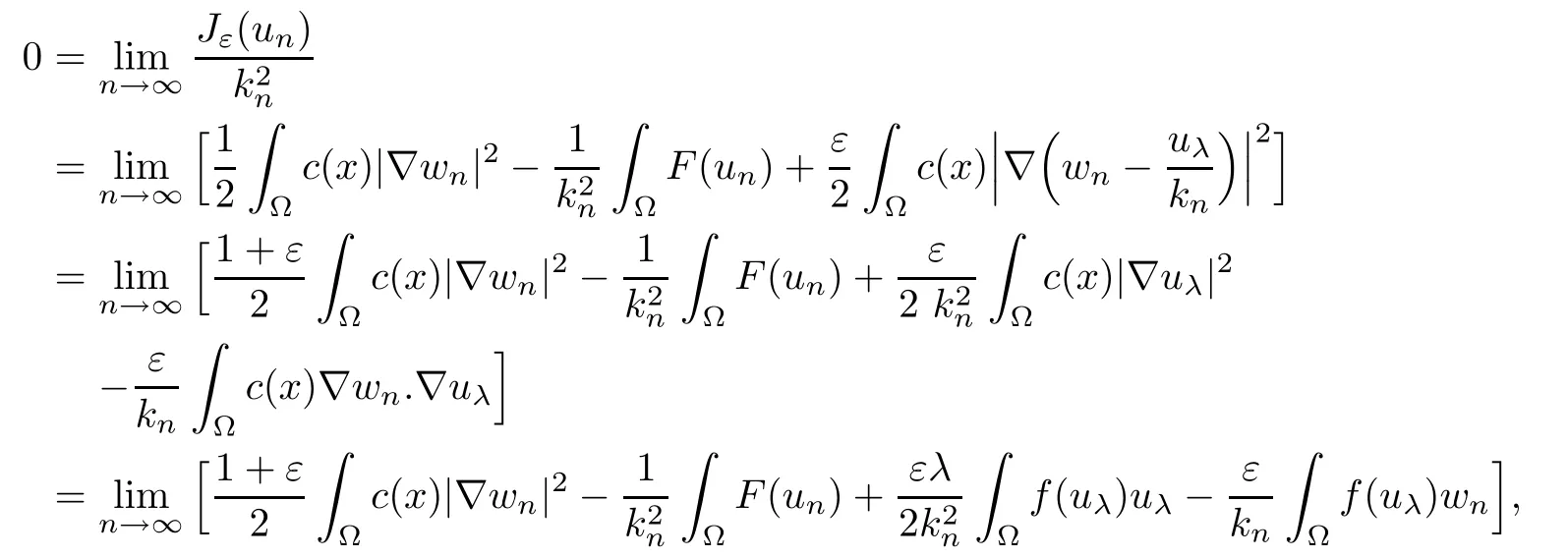
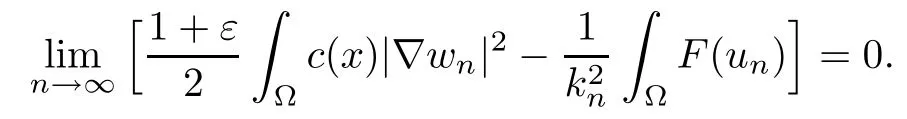
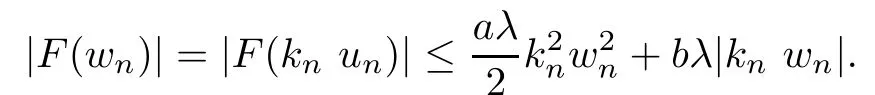

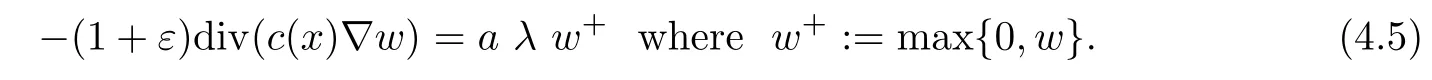

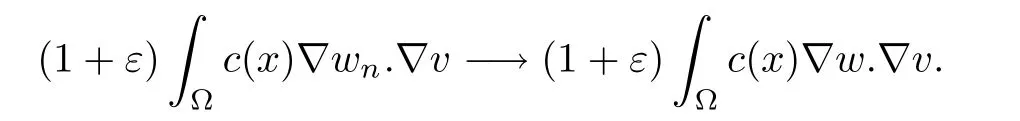
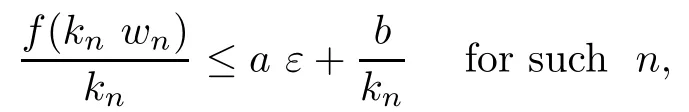

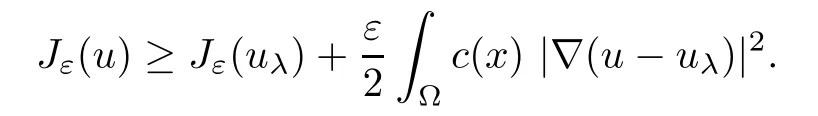
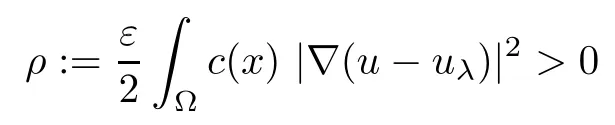
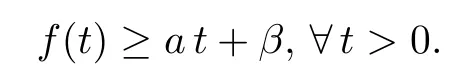

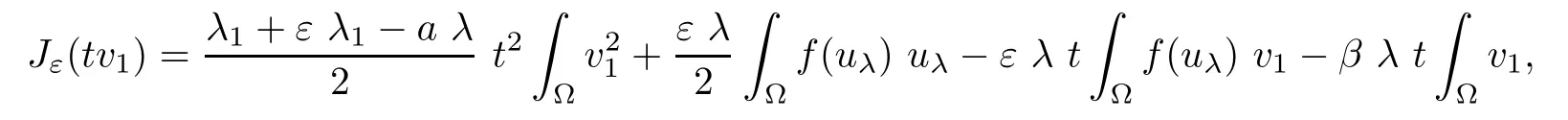
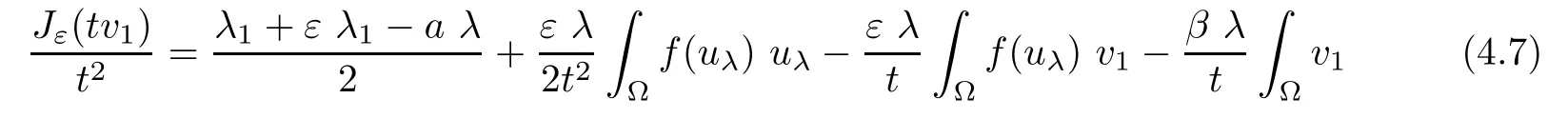



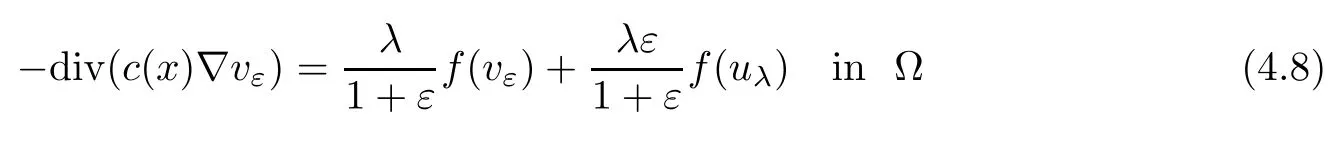

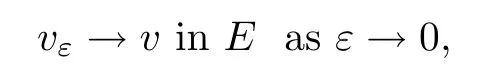

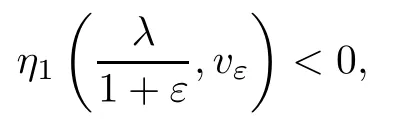


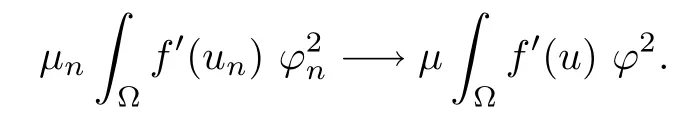
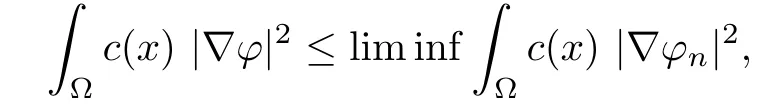
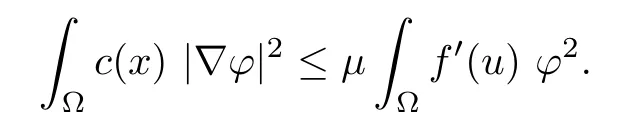

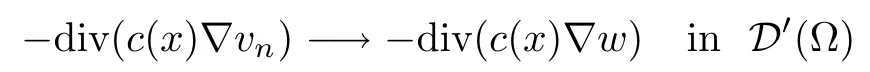
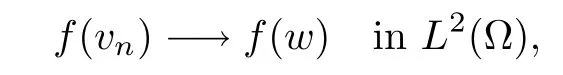





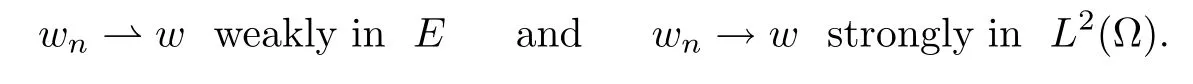

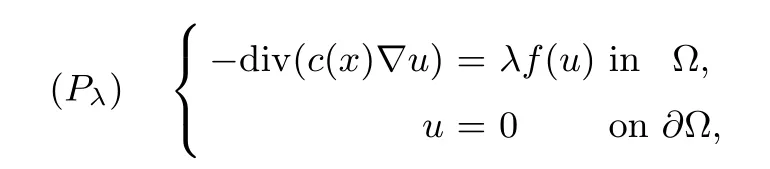
 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
- Acta Mathematica Scientia(English Series)的其它文章
- NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS∗
- THREE SOLUTIONS FOR A FRACTIONAL ELLIPTIC PROBLEMS WITH CRITICAL AND SUPERCRITICAL GROWTH∗
- SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES∗
- MULTIPLICITY RESULTS FOR A NONLINEAR ELLIPTIC PROBLEM INVOLVING THE FRACTIONAL LAPLACIAN∗
- EXISTENCE AND UNIQUENESS OF NON-TRIVIAL SOLUTION OF PARABOLIC p-LAPLACIAN-LIKE DIFFERENTIAL EQUATION WITH MIXED BOUNDARIES∗
- PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS∗
