SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES∗

Xiaosong LIU(刘小松)

School of Mathematics and Computational Science,Lingnan Normal University, Zhanjiang 524048,China

Taishun LIU(刘太顺)

Department of Mathematics,Huzhou University,Huzhou 313000,China

SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES∗

Xiaosong LIU(刘小松)

School of Mathematics and Computational Science,Lingnan Normal University, Zhanjiang 524048,China

E-mail:lxszhjnc@163.com

Taishun LIU(刘太顺)

Department of Mathematics,Huzhou University,Huzhou 313000,China

E-mail:tsliu@hutc.zj.cn

In this article,frst,the sharp estimates of all homogeneous expansions for a subclass of quasi-convex mappings of type B and order α on the unit ball in complex Banach spaces are given.Second,the sharp estimates of all homogeneous expansions for the above generalized mappings on the unit polydisk in Cnare also established.In particular, the sharp estimates of all homogeneous expansions for a subclass of quasi-convex mappings (include quasi-convex mappings of type A and quasi-convex mappings of type B)in several complex variables are get accordingly.Our results state that a weak version of the Bieberbach conjecture for quasi-convex mappings of type B and order α in several complex variables is proved,and the derived conclusions are the generalization of the classical results in one complex variable.

homogeneous expansion;quasi-convex mapping of type B and order α;quasiconvex mapping;quasi-convex mapping of type A;quasi-convex mapping of type B

2010 MR Subject Classifcation32A30;32H02

1 Introduction

In geometric function theorey of one complex variable,people show great interest in the following classical theorem.

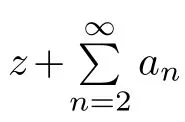
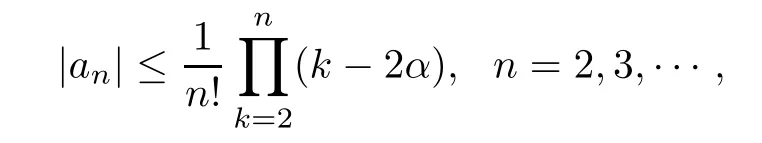
We are naturally to ask whether the corresponding result in several complex variables holds or not?In this article,we shall in part provide an afrmative answer.

Concerning the sharp estimates of all homogeneous expansions for a subclass of quasi-convex mappings(include quasi-convex mappings of type A and quasi-convex mappings of type B)in several complex variables,it was shown that the above result in general is invalid(see[13]). However,on a special domain,such as the unit polydisk in Cn,Liu[7],Liu and Liu[9]obtained the sharp estimates of all homogeneous expansions for quasi-convex mappings(include quasiconvex mappings of type A and quasi-convex mappings of type B)under diferent restricted conditions respectively.On the other hand,Liu and Liu[8]derived the sharp estimates of all homogeneous expansions for a subclass of quasi-convex mappings of type B and order α (include quasi-convex mappings,quasi-convex mappings of type A and quasi-convex mappings of type B).We mention that the family of quasi-convex mappings of type B and order α is a signifcant family of holomorphic mappings in several complex variables,and the Bieberbach conjecture in several complex variables(i.e.,the sharp estimates of all homogeneous expansions for biholomorphic starlike mappings on the unit polydisk in Cnhold)(see[1,3,10])is a very signifcant and extremal difcult problem.Owing to this reason,the sharp estimates of all homogeneous expansions for quasi-convex mappings of type B and order α seem to be a meaningful problem as well.

Let X denote a complex Banach space with the norm k.k,let X∗denote the dual space of X,let B be the open unit ball in X,and let U be the Euclidean open unit disk in C.We also denote by Unthe open unit polydisk in Cn,Bnthe Euclidean unit ball in Cnand N∗the set of all positive integers.Let∂Undenote the boundary of Un,(∂U)nbe the distinguished boundary of Un.Let the symbol′mean transpose.For each x∈X{0},we defne

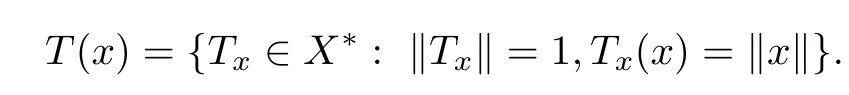
By the Hahn-Banach theorem,T(x)is nonempty.

Let H(B)be the set of all holomorphic mappings from B into X.We know that if f∈H(B), then

for all y in some neighborhood of x∈B,where Dnf(x)is the nth-Fr´echet derivative of f at x, and for n≥1,

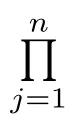
We say that a holomorphic mapping f:B → X is biholomorphic if the inverse f−1exists and is holomorphic on the open set f(B).A mapping f∈H(B)is said to be locally biholomorphic if the Fr´echet derivative Df(x)has a bounded inverse for each x∈B.If f:B→ X is a holomorphic mapping,then we say that f is normalized if f(0)=0 and Df(0)=I,where I represents the identity operator from X into X.

We say that a normalized biholomorphic mapping f:B→X is a starlike mapping if f(B) is a starlike domain with respect to the origin.

Suppose that Ω∈Cnis a bounded circular domain.The frst Fr´echet derivative and the m(m>2)-th Fr´echet derivative of a mapping f∈H(Ω)at point z∈Ω are written by Df(z),Dmf(z),respectively.

Now we recall some defnitions below.

Defnition 1.1(see[8]) Suppose that α∈[0,1)and f:B→X is a normalized locally biholomorphic mapping.If

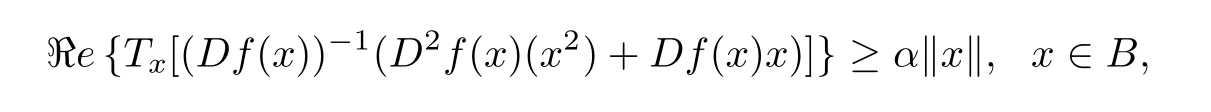
then f is said to be quasi-convex of type B and order α.

Let QαB(B)be the set of all quasi-convex mapping of type B and order α on B.

Defnition 1.2(see[14]) Suppose that f:B→X is a normalized locally biholomorphic mapping,and denote

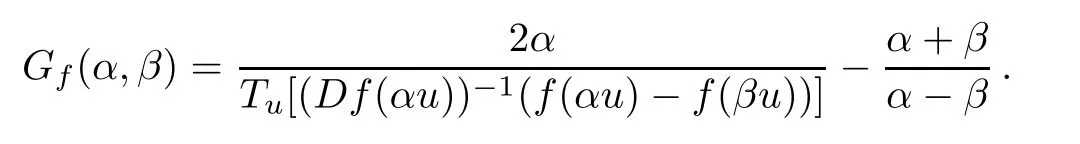
If

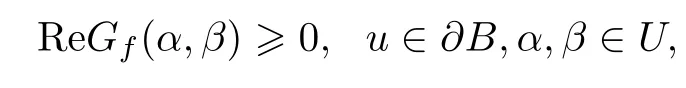
then f is said to be a quasi-convex mapping of type A on B.

We denote by QA(B)the set of all quasi-convex mapping of type A on B.

Defnition 1.3(see[2]) Suppose that f:B→X is a normalized locally biholomorphic mapping.If

then f is said to be a quasi-convex mapping of type B on B.

We refer to the set QB(B)as the set of all quasi-convex mapping of type B on B.

When X=Cn,Defnitions 1.1 and 1.2 are the same defnitions which were introduced by Roper and Sufridge[13].

Defnition 1.4(see[14]) Suppose that f:B→X is a normalized locally biholomorphic mapping.If

then f is said to be a quasi-convex mapping on B.

Let Q(B)be the set of all quasi-convex mapping of type B on B.Gong[2]proved the inclusion relation

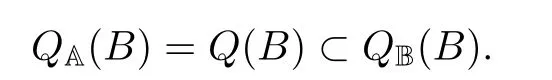
Indeed,Defnitions 1.2,1.3 and 1.4 reduce to the criteria of biholomorphic convex functions in one complex variable.

Defnition 1.5(see[5]) Let f∈H(B).It is said that f is k-fold symmetric if

Defnition 1.6(see[6]) Suppose that Ω is a domain(connected open set)in X which contains 0.It is said that x=0 is a zero of order k of f(x)if f(0)=0,···,Dk−1f(0)=0,but Dkf(0)6=0,where k∈N∗.

According to Defnitions 1.4 and 1.5,it is easily shown that x=0 is a zero of order k+1 (k∈N)of f(x)−x if f is a k-fold symmetric normalized holomorphic mapping f(x)(f(x)6≡x) defned on B.However,the converse is fail.

Let QA,k+1(B)(resp.QB,k+1(B),Qk+1(B))be the subset of QA(B)(resp.QB(B),Q(B)) of mappings f such that z=0 is a zero of order k+1 of f(z)−z.

2 Sharp Estimates of All Homogeneous Expansions for a Subclass of Quasi-convex Mappings of Type B and Order α on the Unit Ball of Complex Banach Spaces

In order to prove the desired results in this section,we need to provide some lemmas as follows.

Lemma 2.1Let α∈[0,1),f,p:B→ C∈H(B),f(0)=p(0)=1,f(e2πikx)=f(x), p(e2πikx)=p(x)(k∈N∗),and f(x)+3Df(x)x+D2f(x)(x2)=(f(x)+Df(x)x)(α+(1−α)p(x)). Then

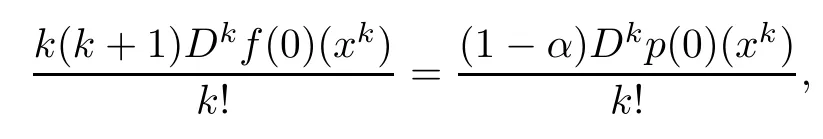
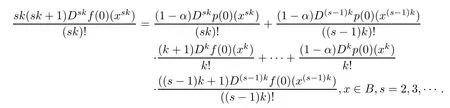
ProofIn view of the hypothesis of Lemma 2.1,we have

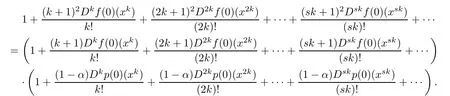
A simple calculation shows that

Compare the homogeneous expansions of the two sides in the above equality.We derived the desired result.

Lemma 2.2Let α∈[0,1),f,p:B→C∈H(B),f(0)=p(0)=1.If x=0 is a zero of order k+1(k∈N∗)of xf(x)−x(resp.xp(x)−(x)),and f(x)+3Df(x)x+D2f(x)(x2)= (f(x)+Df(x)x)(α+(1−α)p(x)),then for any x∈B,

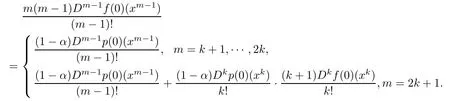
ProofAccording to the conditions of Lemma 2.2,we obtain

A direct computation shows that

Compare the homogeneous expansions of the two sides in the above equality.It follows the desired result.

We now begin to establish the desired results in this section.

Theorem 2.1Let α∈[0,1),f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)= xf(x)∈QαB(B),and F is a k(k∈N∗)-fold symmetric mapping on B.Then

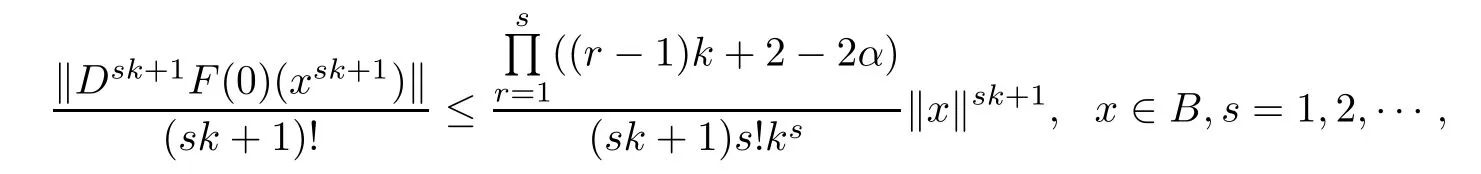
and the above estimates are sharp.

ProofLet W(x)=(DF(x))−1D(DF(x)x)x.A straightforward computation shows that

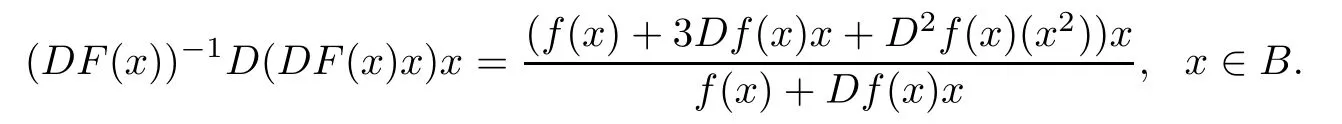
Since F(x)=xf(x)∈QαB(B),then according to Defnition 1.1,we see that

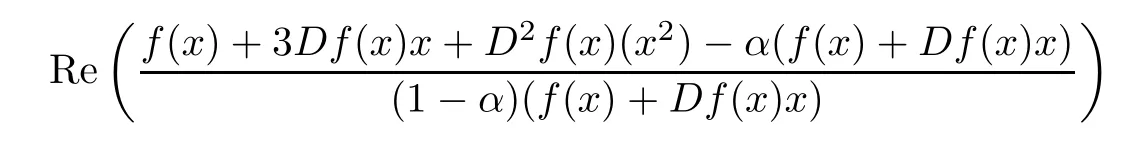
Letting

then p:B→C∈H(B),p(0)=f(0)=1,

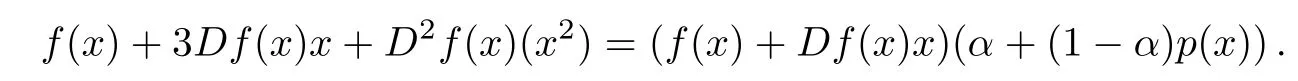
Also since F(x)=xf(x)is a k(k∈N∗)-fold symmetric mapping,then f(e2πikx)=f(x)and p(e2πi

kx)=p(x).We now deduce that

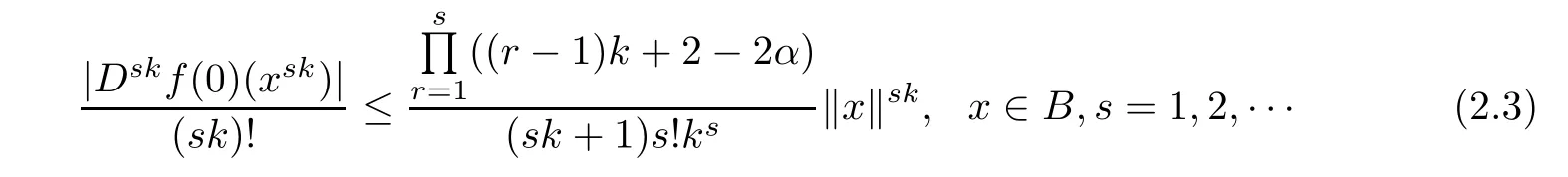
hold by inductive method.When s=1,(2.3)holds from Lemma 2.1 and[11,Lemma 2.2](the case m=k+1).We assume that

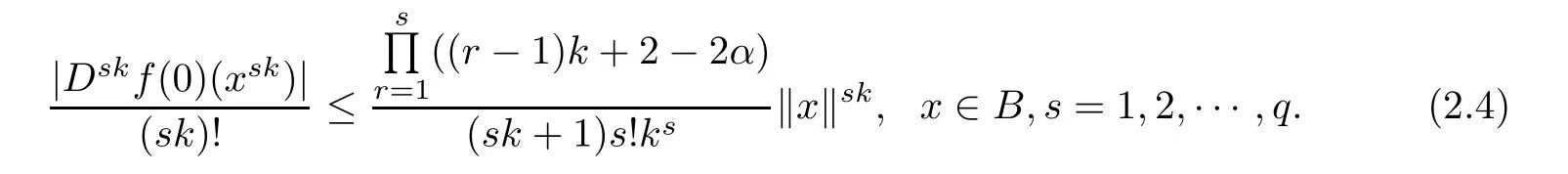
It sufces to prove that(2.3)holds for s=q+1.For this purpose,by applying Lemma 2.1, (2.4)and[11,Lemma 2.2],we know that

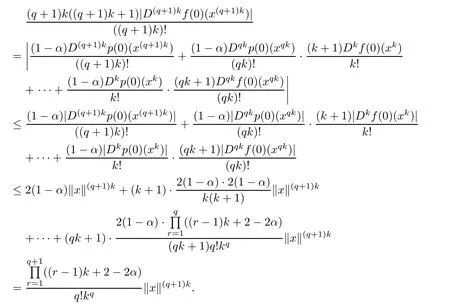
That is

Note that

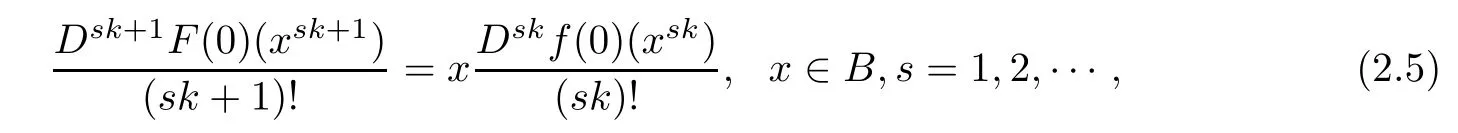
when F(x)=xf(x).Therefore in view of(2.3)and(2.5),it follows the result,as desired.

It is easy to check that

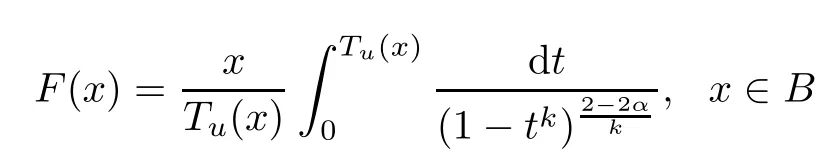
satisfes the condition of Theorem 2.1,where kuk=1.Taking x=ru(0≤r<1),it yields that

We see that the estimates of Theorem 2.1 are sharp. ?

Put α=0 in Theorem 2.1.Then we obtain the following corollary immediately.

Corollary 2.1Let f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)=xf(x)∈QB(B),and F is a k(k∈N∗)-fold symmetric mapping on B.Then

and the above estimates are sharp.

Note that f(x)+Df(x)x 6=0,x∈B due to the growth theorem of F(x)=xf(x)∈QA(B) (or Q(B))and

from S∗(B)⊂QA(B)=Q(B)and Q(B)=QA(B)⊂QB(B)(see[2]).We readily get the following corollary from Corollary 2.1.

Corollary 2.2Let f:B→C∈H(B),F(x)=xf(x)∈QA(B)(resp.Q(B)),and F is a k(k∈N∗)-fold symmetric mapping on B.Then

and the above estimates are sharp.

By making use of Theorem 2.1,the Taylor expansion of F(x)=xf(x)and the triangle inequality of the norm in complex Banach spaces,we deduce the following two corollaries immediately(the details of the proof are omitted here).

Corollary 2.3Let α∈[0,1),f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)= xf(x)∈QαB(B),and F is a k(k∈N∗)-fold symmetric mapping.Then

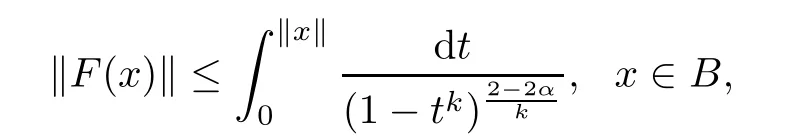
and the above estimate is sharp.

The example of the sharpness of Corollary 2.1 is similar to that in Theorem 2.1,we need only to mention that

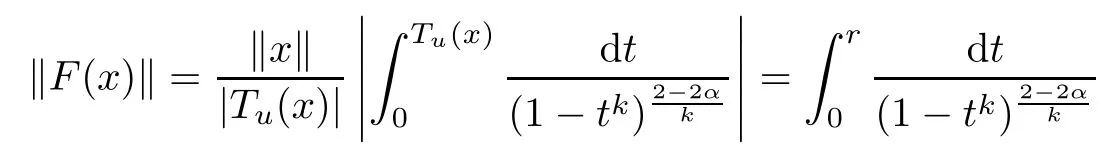
holds for x=ru(0≤r<1).

Corollary 2.4Let α∈[0,1),f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)= xf(x)∈QαB(B),and F(x)is a k(k∈N∗)-fold symmetric mapping,where B is the unit ball of a complex Hilbert space X.Then

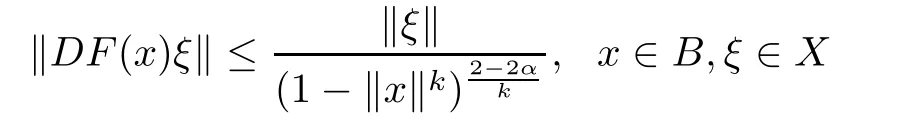
and the above estimate is sharp.

ProofAccording to Corollary 2.1,triangle inequalities with respect to the norm in complex Banach spaces and the fact

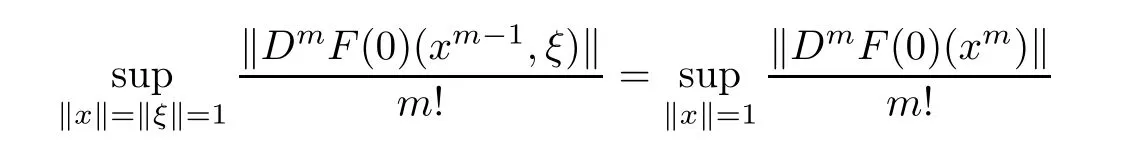
(see[4]),then it follows the result,as desired.Considering

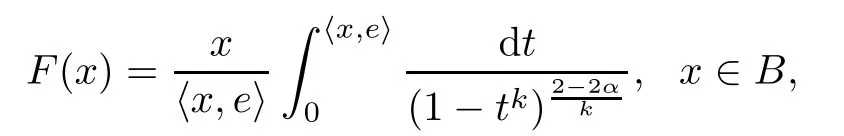
where kek=1,then F satisfes the conditions of Corollary 2.4.It is shown that

by a direct calculation.We set x=re,ξ=Re(0≤r<1,R≥0).Then

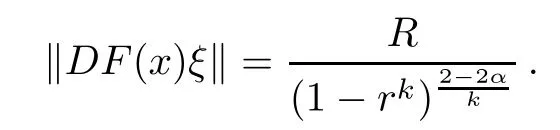
We see that the estimate of Corollary 2.4 is sharp. ?

Taking α=0 in Corollaries 2.3 and 2.4,we directly obtain the corollaries as follows.

Corollary 2.5Let f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)=xf(x)∈QB(B),and F is a k(k∈N∗)-fold symmetric mapping.Then

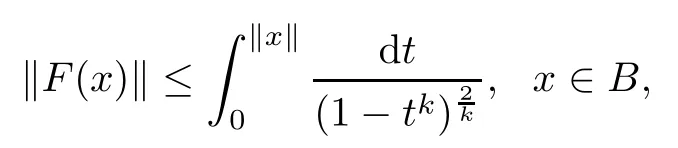
and the above estimate is sharp.

Corollary 2.6Let f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)=xf(x)∈QB(B),and F(x)is a k(k∈N∗)-fold symmetric mapping,where B is the unit ball of a complex Hilbert space X.Then

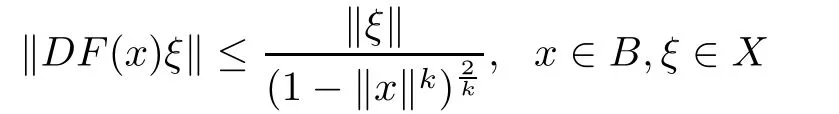
and the above estimate is sharp.

With the analogous explanation of Corollary 2.4,we get the following corollary from Corollary 2.6.

Corollary 2.7Let f:B→C∈H(B),F(x)=xf(x)∈Q(B)(or QA(B)),and F(x)is a k(k∈N∗)-fold symmetric mapping,where B is the unit ball of a complex Hilbert space X. Then

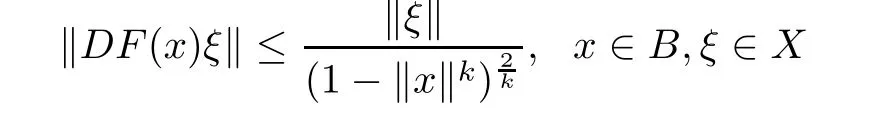
and the above estimate is sharp.

Remark 2.1The sharp growth and covering theorem for QA(B)(resp.Q(B))was given by Roper and Sufridge[13](the case of fnite dimension)(resp.Zhang and Liu[14](the case of infnite dimension)).However,up to now,the sharp growth and covering theorem for QB(Un), and the sharp distortion theorem for QA(Un)(Q(Un)and QB(Un)are still open problems in several complex variables.

Theorem 2.2Let α∈[0,1),f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)= xf(x)∈QαB,k+1(B).Then

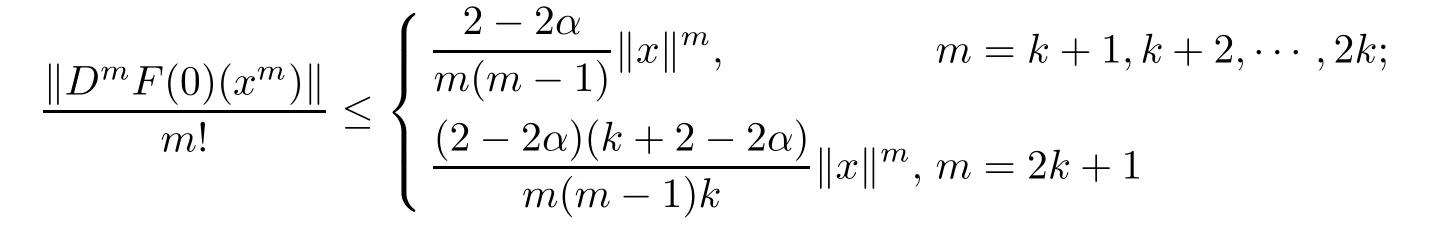
for x∈B.The above estimates are sharp for m=k+1 and m=2k+1.

ProofIn view of the hypothesis of Theorem 2.2,Lemma 2.2 and[11,Lemma 2.2],it yields that

and

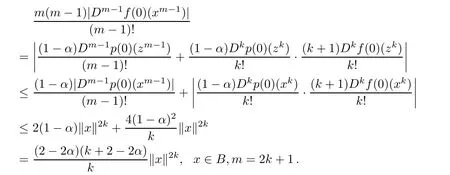
Noticing that

if F(x)=xf(x).Then we derive the desired result.The example which shows the sharpness of Theorem 2.2 is similar to that in Theorem 2.1.

Letting α=0,it is easy to obtain the corollary as follow.

Corollary 2.8Let f:B→C∈H(B),f(x)+Df(x)x 6=0,x∈B,F(x)=xf(x)∈QB,k+1(B).Then

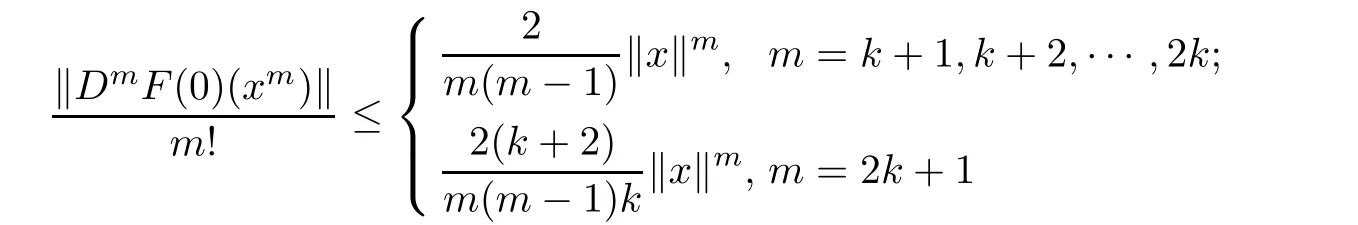
for x∈B.The above estimates are sharp for m=k+1 and m=2k+1.

Similar to that in the explanation of Corollary 2.4,we drive the following corollary from Corollary 2.8.

Corollary 2.9Let f:B→C∈H(B),F(x)=xf(x)∈Qk+1(B)(or QA,k+1(B)).Then

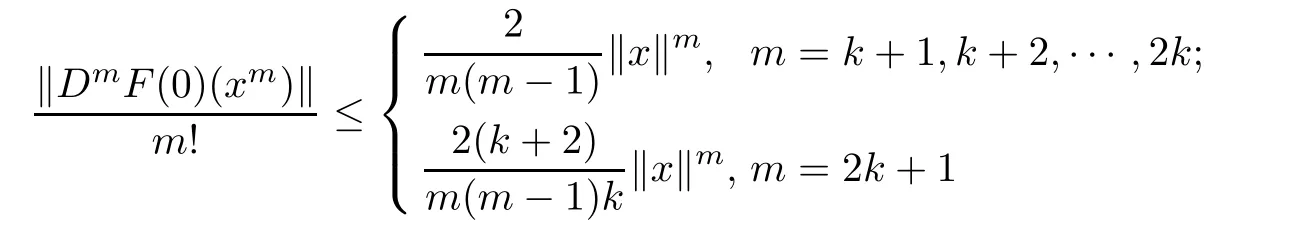
for x∈B.The above estimates are sharp for m=k+1 and m=2k+1.

3 Sharp Estimates of All Homogeneous Expansions for a Subclass of Quasi-convex Mappings of Type B and Order α on the Unit Polydisk in Cn

In this section,let each mjbe a non-negative integer,N=m1+m2+···+mn∈N∗,and mj=0 implies that the corresponding components in Z and F(Z)are omitted.Uml(resp. UN)is denoted by the unit polydisk of Cml(l=1,2,···,n)(resp.CN).

It is necessary to establish the following lemmas in order to get the desired results in this section.

Lemma 3.1(see[8]) Suppose that α∈[0,1),and f is a normalized locally biholomorphic mapping on Un.Then f∈QKαB(Un)if and only if

Theorem 3.1Let α∈[0,1),fl:Uml→C∈H(Uml),fl(Zl)+Dfl(Zl)Zl6=0,Zl∈Uml, l=1,2,···,n,F(Z)=(F1(Z1),F2(Z2),···,Fn(Zn))′=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))′∈QαB(UN),and F is a k(k∈N∗)-fold symmetric mapping.Then

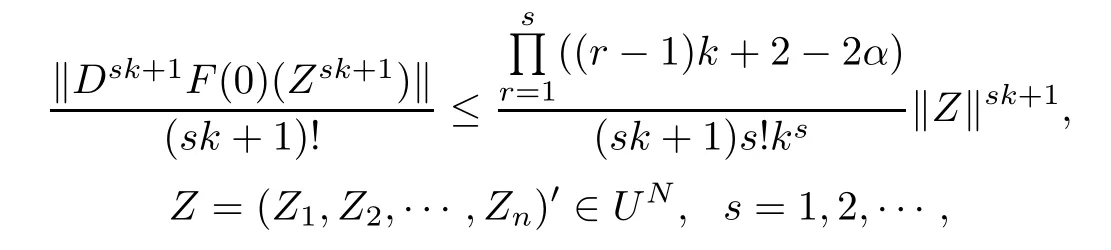
and the above estimates are sharp.

ProofIn view of the condition of Theorem 3.1,for any Z=(Z1,Z2,···,Zn)′∈UN,it is shown that

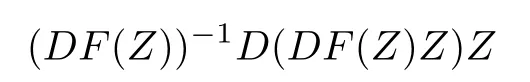
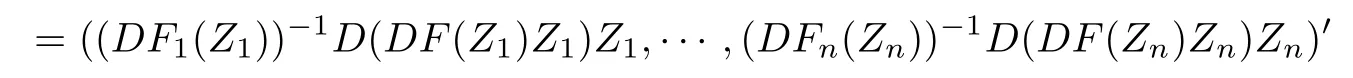
by a direct calculation.We pay attention to that

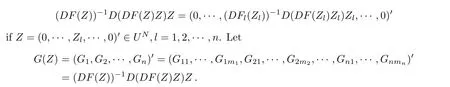
Then we know that

from Lemma 3.1.Noticing that

here kZlkml(resp.kZkN)is briefy denoted by kZlk(resp.kZk),it follows the desired result.

For any Z=(Z1,Z2,···,Zn)′∈UN,it is not difcult to check that

satisfes the condition of Theorem 3.1,where Zl=(Zl1,Zl2,···,Zlml)′∈Uml,l=1,2,···,n. We set Zl=(R,0,···,0)′(0≤R<1),l=1,2,···,n.It is easy to obtain

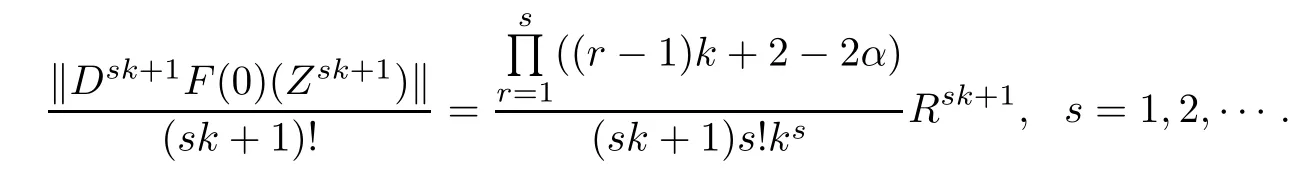
Hence the estimates of Theorem 3.1 are sharp.

We set α=0 in Theorem 3.1.Then we easily get the following corollary.

Corollary 3.1Let fl:Uml→ C∈H(Uml),fl(Zl)+Dfl(Zl)Zl6=0,Zl∈Uml,l= 1,2,···,n,F(Z)=(F1(Z1),F2(Z2),···,Fn(Zn))′=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))′∈QB(UN),and F is a k(k∈N∗)-fold symmetric mapping.Then

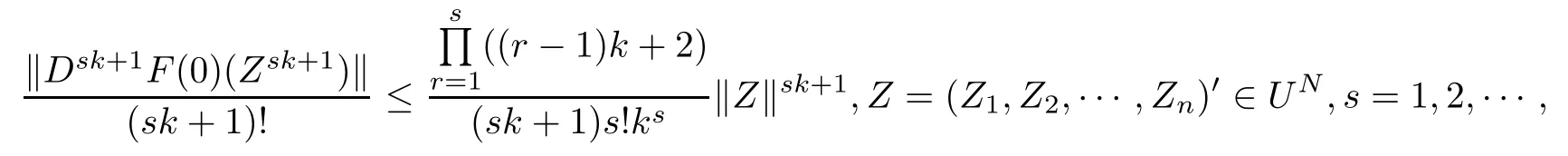
and the above estimates are sharp.

With the similar interpretation of Corollary 2.4,it is apparent to obtain the corollary as follow.

Corollary 3.2Let fl:Uml→C∈H(Uml),l=1,2,···,n,F(Z)=(F1(Z1),F2(Z2),···, Fn(Zn))′=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))′∈Q(UN)(QA(UN)),and F is a k(k∈N∗)-fold symmetric mapping.Then

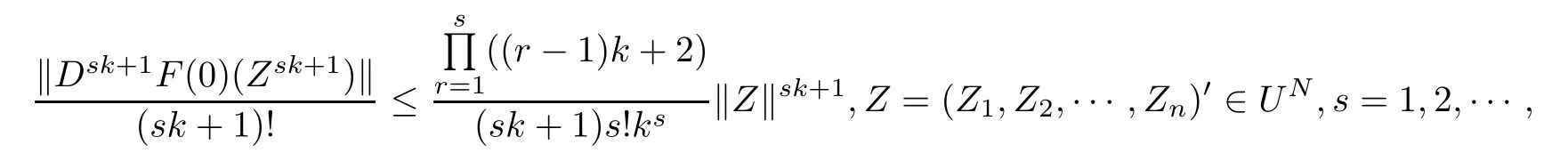
and the above estimates are sharp.

Theorem 3.2Let α∈[0,1),fl:Uml→C∈H(Uml),fl(Zl)+Dfl(Zl)Zl6=0,Zl∈Uml, l=1,2,···,n,F(Z)=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))′∈QαB,k+1(UN).Then

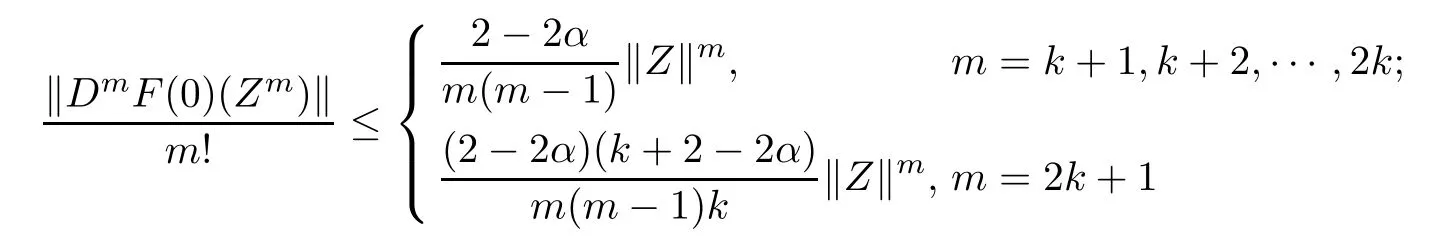
for Z=(Z1,Z2,···,Zn)′∈UN.The above estimates are sharp for m=k+1 and m=2k+1.

ProofWith the analogous arguments as in the proof of Theorem 2.2,it follows the desired result. ?

Put α=0 in Theorem 3.2.Then we readily obtain the following corollary.

Corollary 3.3Let fl:Uml→ C∈H(Uml),fl(Zl)+Dfl(Zl)Zl6=0,Zl∈Uml,l= 1,2,···,n,F(Z)=(Z1f1(Z1),Z2f2(Z2),···,Znfn(Zn))′∈QB,k+1(UN).Then

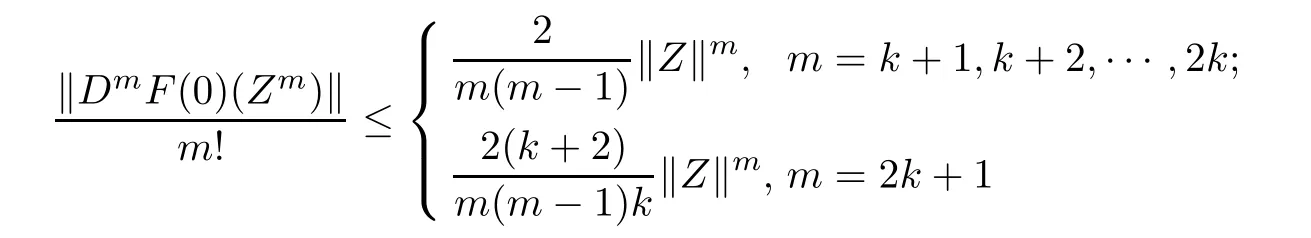
for Z=(Z1,Z2,···,Zn)′∈UN.The above estimates are sharp for m=k+1 and m=2k+1.

Similar to that in the interpretation of Corollary 2.2,we easily obtain the corollary as follow.

Corollary 3.4Let fl:Uml→C∈H(Uml),l=1,2,···,n,F(Z)=(Z1f1(Z1),Z2f2(Z2), ···,Znfn(Zn))′∈Qk+1(UN)(QA,k+1(UN)).Then

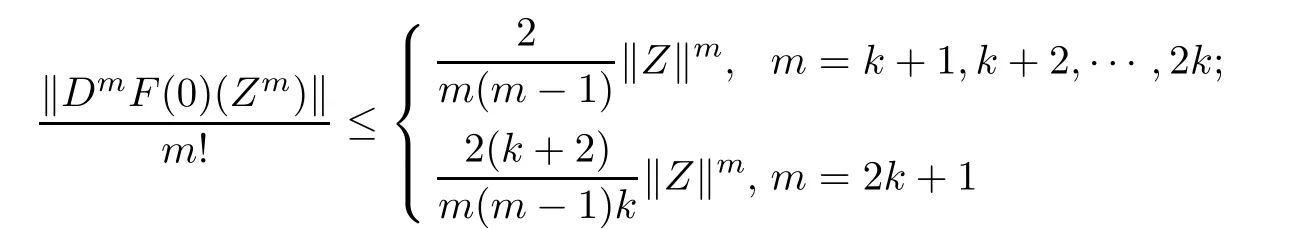
for Z=(Z1,Z2,···,Zn)′∈UN.The above estimates are sharp for m=k+1 and m=2k+1.

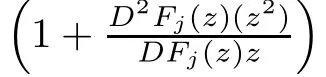
and the above estimates are sharp.

ProofFixWe writeLet

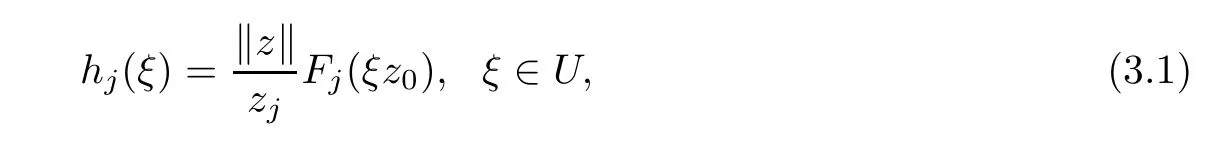
by a simple calculation.Therefore,we have

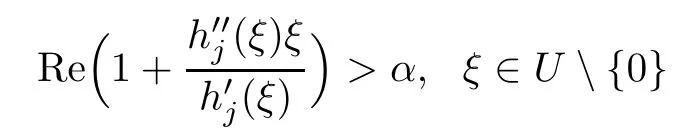
It is also easy to know that

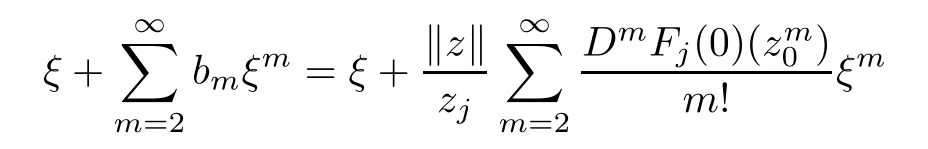
from(3.1).Comparing the coefcients of the two sides in the above equality,it is shown that

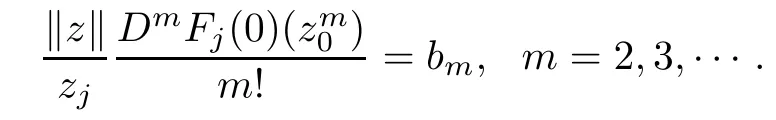
Hence,by Theorem 2.1(the case X=C,B=U),we conclude that

When z0∈(∂U)n,it yields that

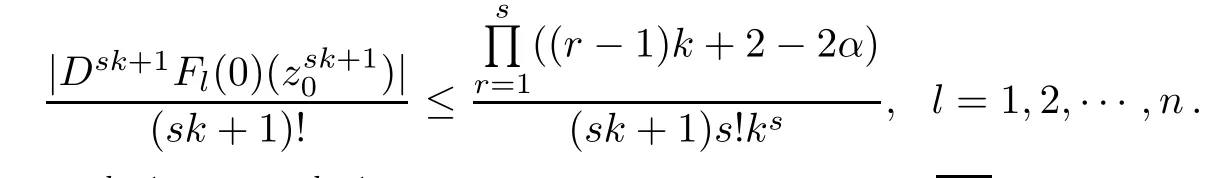
Also in view of Dsk+1Fl(0)(zsk+1)is a holomorphic function on Un,we have

by the maximum modulus theorem of holomorphic functions on the unit polydisk.This implies that

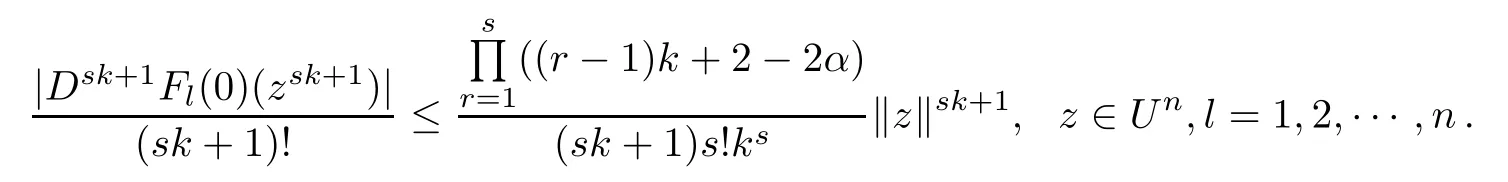
Therefore,

It is not difcult to verify that

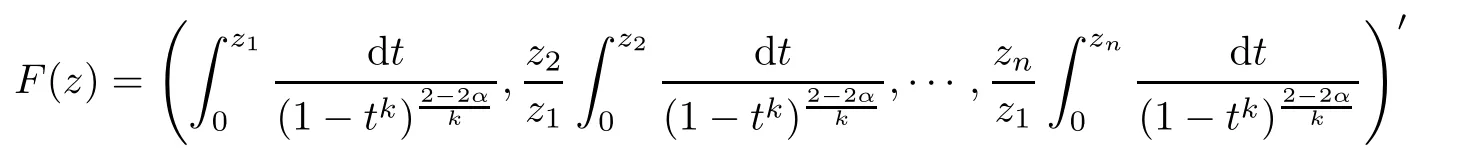
satisfes the condition of Theorem 3.3.Put z=(r,0,···,0)′(0≤r<1),we see that

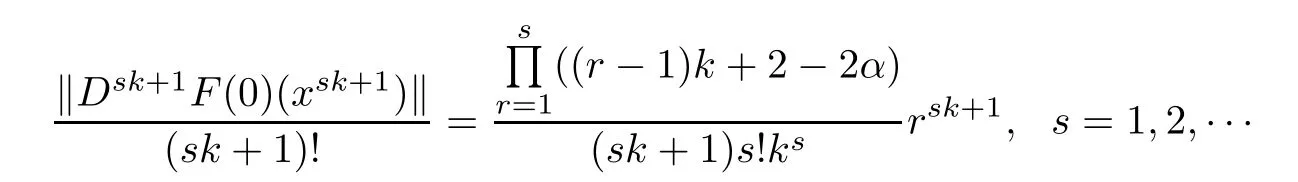
by a direct computation.Then we know that the sharpness for the estimates of Theorem 3.3.

Taking α=0 in Theorem 3.3,we get the following corollary immedately.

and the above estimates are sharp.

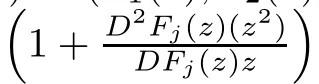
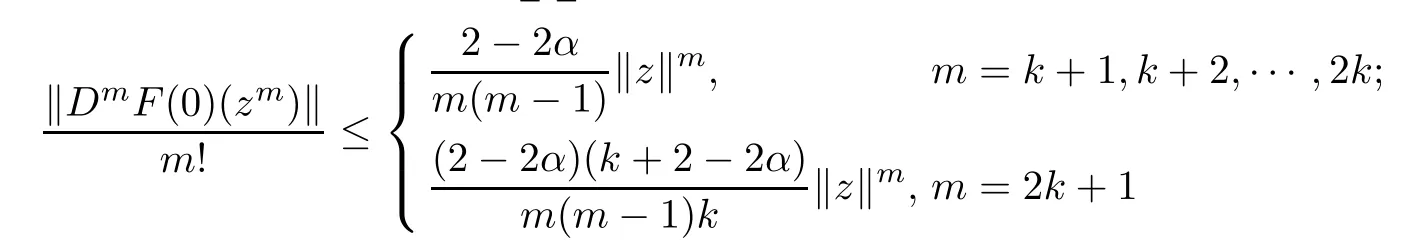
for z=(z1,z2,···,zn)′∈Un.The above estimates are sharp for m=k+1 and m=2k+1.

We set α=0 in Theorem 3.4.Then it is obvious to obtain the corollary as follow.

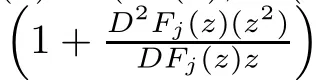
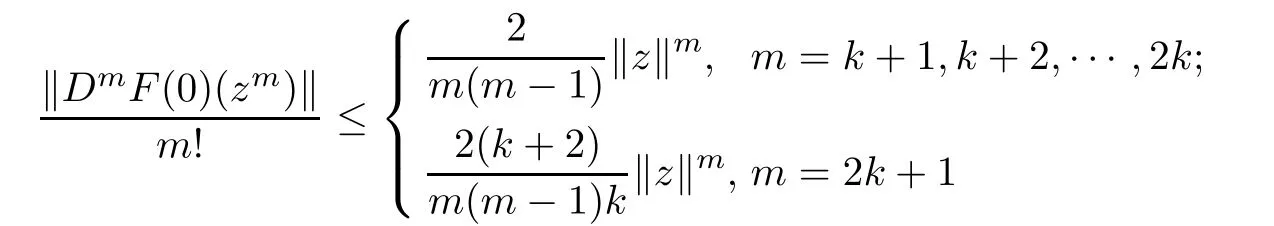
for z=(z1,z2,···,zn)′∈Un.The above estimates are sharp for m=k+1 and m=2k+1.

Remark 3.1We see that Theorem 2.1 is the special case of Theorem 3.3 if X=Cn, B=Un,and Theorem 3.1 is the special case of Theorem 3.3 if m1=n,ml=0,l=2,···,n or ml=1,l=1,2,···,n as well.

Remark 3.2It is not difcult to verify that F(z)=zf(z)in general does not satisfy

In view of Theorems 2.1,3.1 and 3.3,we accordingly pose the open problem as follow.

Open problem 3.1Suppose that F∈QαB(Un),and F is a k(k∈N∗)-fold symmetric mapping on Un.Then

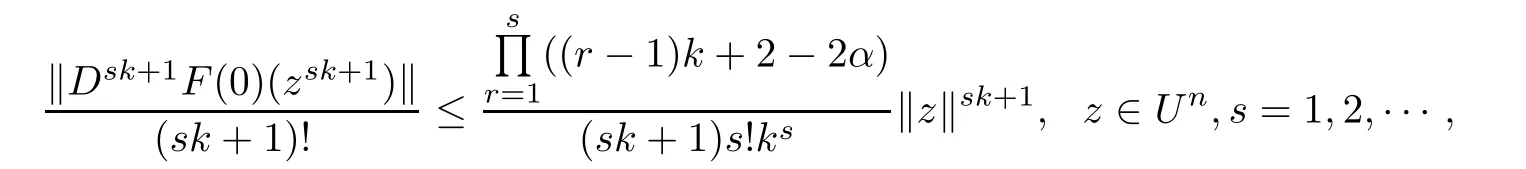
and the above estimates are sharp.

[1]Gong S.The Bieberbach Conjecture.International Press.Providence RI:Amer Math Soc,1999

[2]Gong S.Convex and Starlike Mappings in Several Complex Variables(in Chinese).2nd ed.Beijing:Science Press,2003

[3]Graham I,Kohr G.Geometric Function Theory in One and Higher Dimensions.New York:Marcel Dekker, 2003

[4]H¨ormander L.On a theorem of Graced.Math Scand,1954,2:55–64

[5]Honda T.The growth theorem for k-fold symmetric convex mappings.Bull London Math Soc,2002,34: 717–724

[6]Lin Y Y,Hong Y.Some properties of holomorphic maps in Banach spaces.Acta Math Sinica,1995,38(2): 234–241(in Chinese)

[7]Liu X S.On the quasi-convex mappings on the unit polydisk in Cn.J Math Anal Appl,2007,335:43–55

[8]Liu X S,Liu M S.Quasi-convex mappings of order α on the unit polydisk in Cn.Rocky Mountain J Math, 2010,40:1619–1644

[9]Liu X S,Liu T S.The sharp estimates of all homogeneous expansions for a class of quasi-convex mappings on the unit polydisk in Cn.Chin Ann Math,2011,32B:241–252

[10]Liu X S,Liu T S.The sharp estimate of the third homogeneous expansion for a class of starlike mappings of order α on the unit polydisk in Cn.Acta Math Sci,2012,32B:752–764

[11]Liu X S,Liu T S,Xu Q H.A proof of a weak version of the Bieberbach conjecture in several complex variables.Sci China Math,2015,58:2531–2540

[12]Robertson M S.On the theory of univalent functions.Ann Math,1936,37:374–408

[13]Roper K A,Sufridge T J.Convexity properties of holomorphic mappings in Cn.Trans Amer Math Soc, 1999,351:1803–1833

[14]Zhang W J,Liu T S.The growth and covering theorems for quasi-convex mappings in the unit ball of a complex Banach space.Sci China Ser A-Math,2002,45:1538–1547

∗Received March 24,2015;revised December 23,2015.Supported by National Natural Science Foundation of China(11471111)and Guangdong Natural Science Foundation(2014A030307016).